基于模式识别技术的变压器故障诊断
2022-04-08徐晶冉
徐晶冉,徐 雯,王 栋
(南京供电公司,江苏 南京 210000)
电网规模不断扩大,对电网的实际运行可靠性提出了新的要求[1-3]。在实际应用中,变压器设备故障的频繁发生,严重影响电网运行的可靠性。因此如何有效实现变压器故障诊断是维修人员保障电网稳定运行的基础和前提[4-6]。
变压器故障诊断问题是业内人士关注的焦点,经专家、学者大量深入的研究,得出很多方法[7-9]。有学者提出深度学习的变压器故障诊断模型,分析并用典型数据集对其分类性能进行测试。在此基础上结合变压器油中溶解气体分析数据的确定值,它使用油中溶解气体分析结果作为故障分类属性。该模型故障诊断速度快,但诊断错误较高[10]。有学者提出了支持向量机的变压器故障诊断方法[11],首先采用模糊C均值聚类算法对设备故障样本进行聚类确定值划分,然后支持向量机根据划分结果实现故障类型的诊断。故障诊断准确度高,但诊断速度慢[12]。有学者提出了神经网络的变压器故障检测方法[13],结合熵权算法生成变压器故障特征确定值,采用属性约简算法对特征向量进行属性约简,根据故障特征向量推断变压器故障类型,该方法速度快,故障诊断正确率低[14-16]。传统方法对变压器故障诊断时,均将基准函数的分类门限设置为一个确定值,忽略了类别门限值的变化,无法完成变压器故障诊断,导致变压器故障诊断训练时间长、诊断精度低。
为了解决当前变压器故障诊断过程中存在的问题,提出基于模式识别技术的变压器故障诊断方法。实验结果表明,本文方法能够有效提高模型结果速度和故障诊断的准确度。
1 基于模式识别技术的变压器故障诊断
1.1 确定故障判断门限参数最优值
在传统方法的故障诊断过程中,需要求出故障类别门限值设为确定值,但是在确定门限类别诊断过程中,极易陷入局部最优解。为此本文方法根据混沌粒子群算法确定最优故障类别判断门限参数,然后门限参数建立故障诊断模型,完成变压器故障诊断。
将故障分类的门限总数设置为m个粒子,个体搜索空间为D维,vi=(vi1,vi2,…,viD)为个体i的当前速度,xi=(xi1,xi2,…,xiD)为当前位置,Pi=(Pi1,Pi2,…,PD)为个体i当前最优值,G=(g1,g2,…,gD)为群体当前最优值。个体的速度和位置的更新方式为:
(1)
(2)
式中,d为搜寻的空间维数;ω为惯性权重;c1和c2为个体随机性特征因子;r1和r2为[0,1]内的随机数。
采用混沌算法对故障类别惯性权重进行优化,将其映射至原最优解的空间范围内,避免粒子群算法陷入局部最优,Logistic映射为:
zn+1=μzn(1-zn)
(3)
式中,μ为控制变量;z1,z2,…,zn表示混沌变量。
通过种群迭代过程中,搜索到的最优解在不断更新,考虑到这种情况,需要引入迭代速度因子和聚集度因子,调整种群全局搜索能力,进化因子表达式如下:
(4)
式中,F(gT)和F(gT-1)分别为当代和上一代全局搜索最优值。
分析式(4)可知,h值越大相应的迭代速度越慢,相反该值越小说明迭代速度越快。当ESF的值在恒为1时,说明搜寻结束。
为了在种群搜索阶段增加自适应机制,扩大种群可搜索的最优解空间,通过上述过程设定种群个体搜索阶段的惯性权重:
ω=ωini-hωh+sωs
(5)
式中,ωini为ω的初始值;ωh和ωs分别为ESF和CF的权值。
在最优解搜索过程中,随机性特征因子c1和c2对搜索结果影响较大,随机性特征因子c1和c2数值较大时,种群中个体会过早收敛,为了提高最优解搜索速度,利用式(6)设定随机性特征因子:
c1(k)=c1in-(c1in-c1fi)k/nmax
(6)
c2(k)=c2in+(c2fi-c2in)k/nmax
(7)
式中,c1in和c1fi分别为c1的初始值和最优值;c2in和c2fi分别为c2的初始值和最优值;nmax为最大迭代次数。
综合上述优化结果,获取最优故障类别判断门限参数uh,根据该参数完成变压器故障诊断门限向量参数的优化:
(8)
1.2 故障诊断方法
根据最优故障类别判断门限参数,引入软化因子将故障诊断基准矩阵中的类型诊断阈值转变成区间数,结合峰值、左右诊断阈值、熵描述白化灰云模型,采用模式识别技术型结合变压器实际运行情况,将确定故障类型诊断各评估指标的权重值,结合灰数白化模型获得故障诊断参数,具体过程如下述:
设共有m个变压器故障类型评价指标,n个评价对象,构成标准矩阵B=(bij)n×m,依据信息熵概念,第j个指标的熵值为:
(9)
式中,χij为j个指标熵值的上限值;H为预测输入值;x为相关向量;n为惯性权重。
第j个指标相应的软化因子为:
(10)
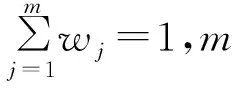
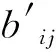
(11)
(12)
λijr=λij,j=1,2,…,m
(13)
式中,λijl、λijr分别为标准值区间的上下限,故障类别区间可表示为[λijl,λij]。
通过式(8)和式(9)得出的熵值建立故障诊断参数的白化灰云模型,该模型将故障样本代入白华权函数计算得出样本的随机模糊特征因子。利用多次计算得出随机理想特征因子,通过计算随机理想特征因子关联故障类别区间,得出故障类别匹配结果,从而完成变压器故障诊断。白化权函数随即特征因子计算步骤为:
(14)
式中,E(t,s)为核函数;Dm为模型的权值;Tm为样本数。
分析式(14)可知,fij值具有随机性,由该值计算得到的样本的随机模糊特征因子白化权值也具有随机性,但它们服从一定的分布规律,通过多次计算,可获得理想的白化权值feij,将此结果作为最终的随机理想特征因子白化权值。
(15)
式中,h为获取最终随机理想特征因子所需运算次数;fijh(x)为通过h次运算获得随机理想特征因子。
计算随机理想特征因子fij与故障类别区间[λijl,λij]的相关度(k),即有:
(16)
式中,n为故障种类数量。
通过计算随机特征因子关联故障类别区间,得出故障类别匹配结果,从而完成变压器故障诊断。
2 仿真实验
2.1 仿真环境
为了测试模式识别技术的变压器故障诊断效果,进行仿真实验,仿真境为:Matlab R2012b CPU intel Pentium(R)Dual-Core E53002.6 GHz,内存2 GB,Windows7操作系统。选择支持向量机和BP神经网络的变压器故障诊断方法进行对比测试,样本构成见表1。采用变压器故障诊断正确率以及诊断效率对性能进行评价。
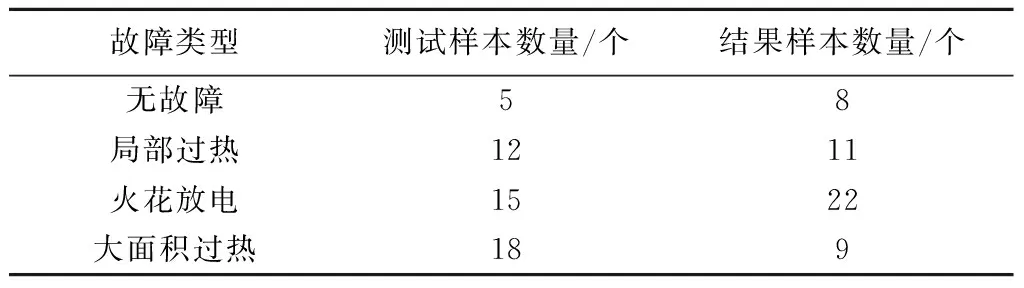
表1 故障样本数据组成Tab.1 Fault sample data composition
2.2 变压器故障诊断结果分析
不同的方法的变压器故障诊断正确率、误诊率、漏诊率分别如图1—图3所示。对图1—图3的变压器故障诊断结果进行对比分析了发现,本文方法的变压器故障诊断正确率大幅度提升,降低了变压器故障诊断的错误率,获得比对比方法更优的变压器故障诊断结果,体现了本文方法的变压器故障诊断优越性。
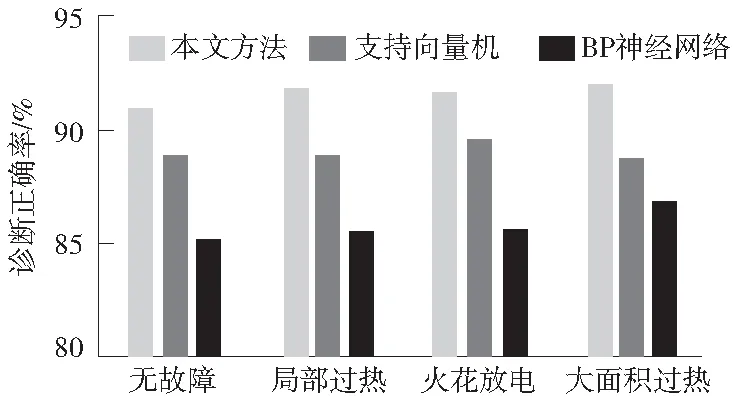
图1 不同方法的变压器故障诊断正确率Fig.1 Correct rate of transformer fault diagnosis by different methods
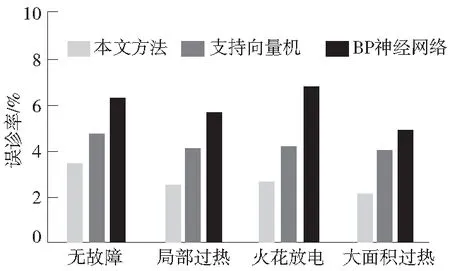
图2 不同方法的变压器故障的误诊率Fig.2 Misdiagnosis rate of transformer faults by different methods
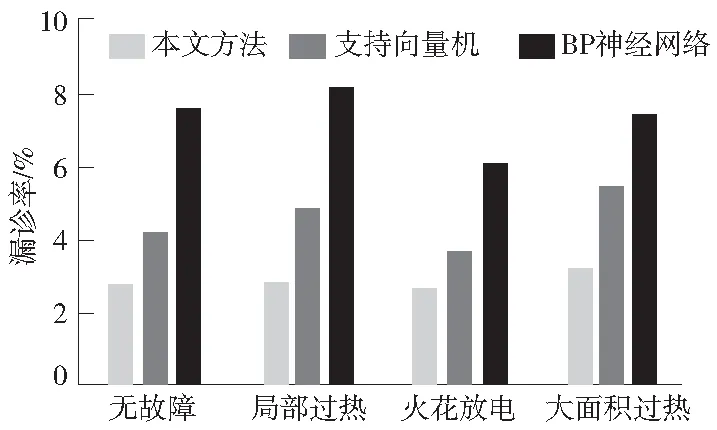
图3 不同方法的变压器故障的漏诊率Fig.3 Missing diagnosis rate of transformer faults with different methods
2.3 变压器故障诊断速度分析
分别利用本文方法和对比方法进行变压器故障诊断实验,它们的迭代次数和均方误差的关系如图4所示。分析图4可知,3种方法均方误差均随着迭代次数的不断增加而减小,采用本文方法对测试样本进行故障诊断时,迭代次数达到70次时,均方误差基本稳定,在0.2左右,BP神经网络在迭代次数达到95次时,均方误差基本稳定,误差为0.27左右,支持向量机方法在迭代次数达到140时,均方误差基本稳定,误差为0.3左右。对比结果表明,本文方法的迭代次数较少,结果速度快,故障诊断效率更高。
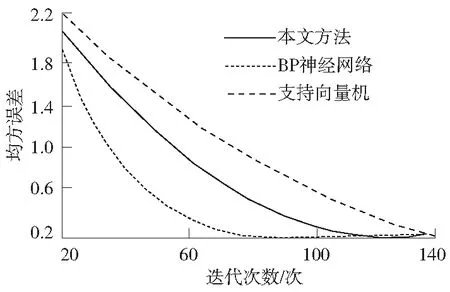
图4 不同方法迭代次数与均方误差的关系Fig.4 Relationship between the number of iterations and the mean square error of different methods
3 结语
变压器故障信息具有不确定性,且故障类型多样,影响了传统的故障诊断方法的结果误差和准确度,提出了模式识别技术的变压器故障诊断方法,有效缩短了变压器故障诊断时间,提高了故障诊断准确度,为解决变压器故障诊断提供了一种有效的解决方案,具有实际应用价值。
