基于价格弹性理论的新能源消费时段和电价组合优化方法
2022-04-08薛璐璐
吴 佳,刘 超,薛璐璐,杨 亮
(1.国网冀北电力有限公司,北京 100053; 2.北京博望华科科技有限公司,北京 100045)
近年来随着电网的不断发展,新能源整合能力不断提升,并入大电网的新能源电力越来越多,新能源在发电中所占的比例也在增加[1-2]。然而,新能源的快速发展也给电力系统的运行带来了一定的风险[3-4],例如新能源出力的抗峰特性增加了电网的调峰压力,导致弃风、弃光现象的增加。因此促进新能源消费,提升新能源利用比率正逐渐成为研究人员关注的焦点。
目前大多数研究都是从调整电价的角度来促进新能源的消费,文献[5]考虑了峰—谷电价实施前后风电场、电网和用户的成本效益,建立了一个综合收益模型来促进新能源的消耗。文献[6-7]通过改变峰—谷电价来提高新能源的消耗。另外一些研究则通过对用户负荷特征的聚类分析来划分峰—谷时段,如模糊聚类[8-9]和k-均值聚类[10-12]等,但上述研究仅从电价或时段的角度进行分析,没有考虑新能源消费与电价、时段的耦合关系,即电价和时段共同促进了新能源的消费。因此上述方法得到的新能源消费量有可能低于实际消费量。
为此,本文提出了一种用电时段和电价的组合优化方法,利用改进的半梯形峰—谷隶属度模型来划分峰—谷时段,采用用电时间和电价为约束函数,基于粒子群算法求解目标函数最优解,最后通过用户对新的峰—谷时段和电价的响应,达到提高新能源消耗的目的。
1 数学模型
1.1 谷—峰时段模型
与传统上基于用户负荷的峰—谷时段划分方法相比,在考虑新能源接入前后的能耗时,应首先考虑新能源的消费情况。因此,综合考虑不同时段的负荷需求和新能源电力产量,本文提出一种改进的半梯形峰—谷隶属度模型来划分峰—谷时段,该模型可用如下公式(1)表示:
(1)
式中,uft、ugt分别为峰—谷成员;L(t)为t时刻的用电量;max(L)、min(L)、max(Lc)、min(Lc)分别为用电量和新能源消耗的最大值和最小值;Lc(t)为时间t时的能源消耗量;u1和u2为用户负载权重。
时间t的取值通过如下公式(2)确定:
(2)
其中Tf、Tp、Tg分别为峰、平、谷时段;m1、m2分别为峰、谷的阈值。
1.2 基于价格弹性理论的用户反应模型
在电力市场环境下,用户可以根据市场电价实时调整用电量以降低电费。一般来说,用户对电价的反应主要包括2种形式:①单次反应。是指用户在一定时期内的用电量,只与当时的电价有关。比如居民照明用电,在电价高的时候,居民可以选择关闭照明,减少用电量。②多时间响应。是指用户在一定时间内的用电量,不仅与当时的电价有关,还与其他时间的电价有关。如企业的生产用电量,该数值不会因为电价较高而停产,企业则反而会根据电价调整生产计划,降低生产成本。
电价和用电量之间的关系如图1所示。由图1可以看出,随着电价上涨,用户成本增加,同时用电量减少。这种关系可以用需求的价格弹性系数方程来描述,如式(3)、式(4)所示:
(3)
(4)
式中,i、j为不同的时间段;Li为i时刻的用电量;Pi、Pj分别为i、j时刻的电价;ΔL、ΔP分别为各时期用电量和电价的变化;ε(i,i)、ε(i,j)分别为自弹性系数和互弹性系数。
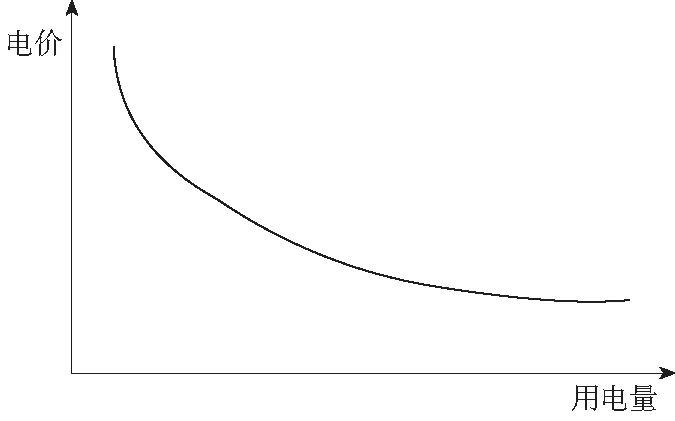
图1 电价与用电量的关系Fig.1 Relationship between electricity price and electricity consumption
基于以上分析,可以得到响应后的用电量,如式(5)所示:
(5)


1.3 新能源消费模型
为了促进新能源的消耗,本文提出了以下响应标准:
(1)响应后用户用电量增加时,传统机组的出力保持不变,先增加新能源的出力,直到新能源的出力达到上限,再增加传统机组的出力。这一关系表示为式(6)、式(7):
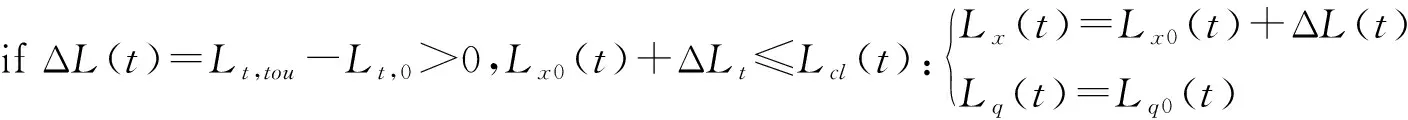
(6)
(7)
式中,Lx0(t)、Lx(t)分别为响应前后的新能源输出值;Lcl(t)为在时间t产生的新能量的数量;Lq0(t)、Lq(t)分别为响应前后t时刻传统单位的输出值。
(2)当用户响应后功耗降低时,新能源的输出保持不变,先降低传统单元的输出,直到传统单元的输出值达到下限,再降低新能源的输出。这种关系表示为式(8)、式(9):
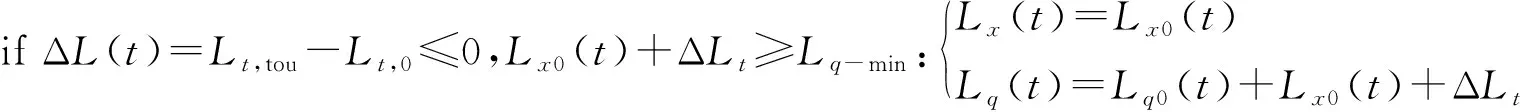
(8)
(9)
式中,Lq-min为传统单位的最小输出。
1.4 用电时段与电价的组合优化模型
(1)用户对电价的满意度模型。在考虑新能源消耗时,还应考虑用户对优化方法的满意度,因此,响应前后总电费的变化被视为用户对电价的满意度。
(10)
式中,Q、Q0分别为响应前后的总电费。
(2)目标函数。本文以新能源消耗最大化和用户满意度最高为目标函数,如式(11)所示:
(11)
式中,Lx0(t)、Lx(t)分别为响应前后的新能耗;θ为用户对电价的满意度;ω1、ω2为权重。
为了使目标函数最大化,将峰值、谷值隶属度阈值m1、m2和用户负荷权重Pf、Pp、Pg用作决策变量。
(3)约束。①时间限制:峰—谷各时段长度不少于6h。②电价约束:为避免峰—谷错位,峰、平、谷期电价应满足式(12)和式(13):
Pf>Pp>Pg
(12)
Pf/Pg≤n
(13)
式中,n为常数,用于限制峰—谷电价比,一般取值为2~5。
2 案例计算与分析
(1)模拟流程图和初始数据。为了验证本文提出的方法的有效性和实用性,以某省电网数据为例进行分析,该省新能源发电数据、用电数据、负荷数据、初始峰—谷期和电价见表1。

表1 峰—谷期与电价Tab.1 Peak valley period and electricity price
本文通过一套由10个发电机组成的电力系统对提出的模型进行了仿真计算分析,该电力系统在24 h内的总用电量需求统计见表2。24 h内的用电量需求和发电量变化曲线如图2所示。
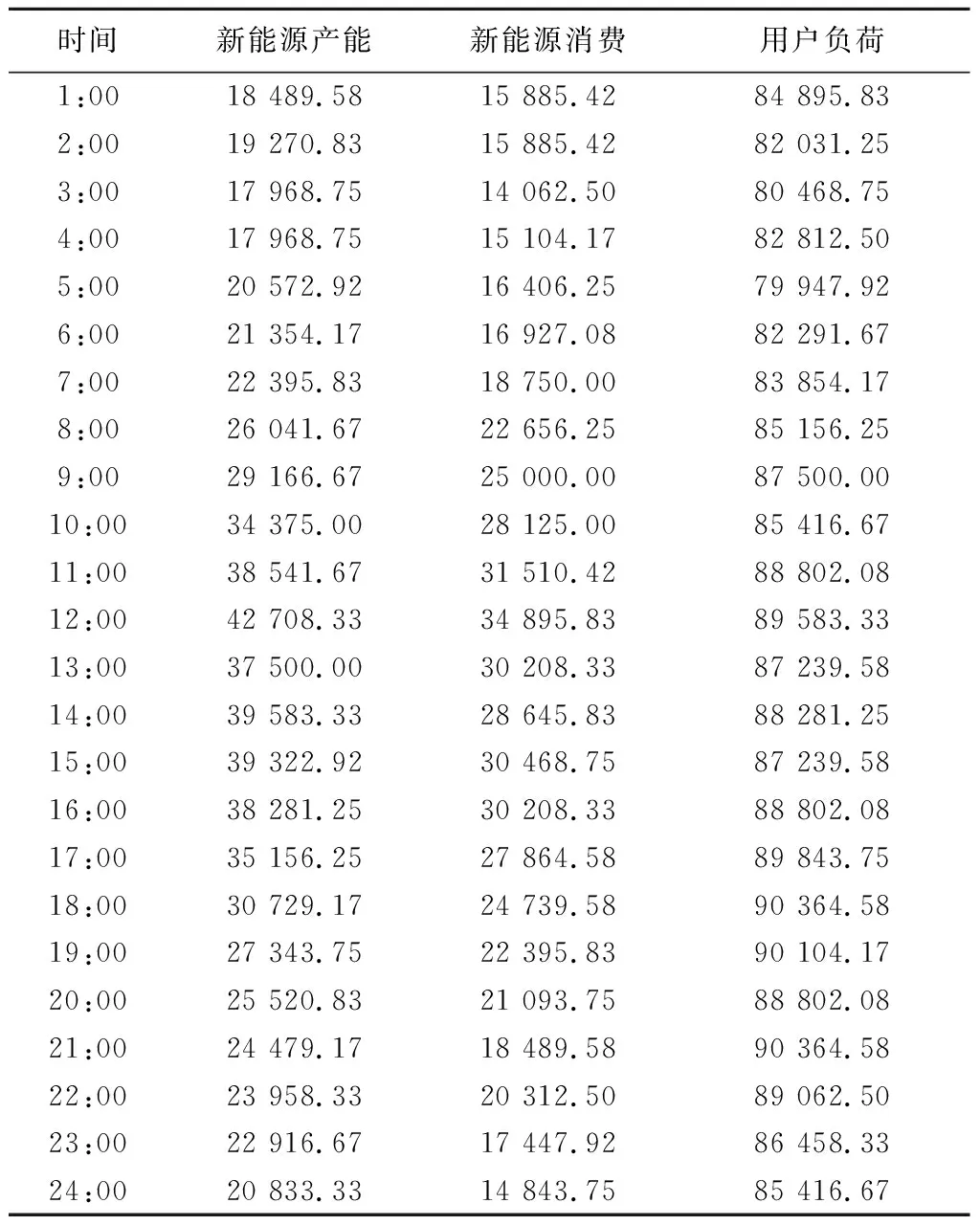
表2 新能源发电与消费、用户负荷统计Tab.2 Statistics of new energy power generation,consumption and user load MW
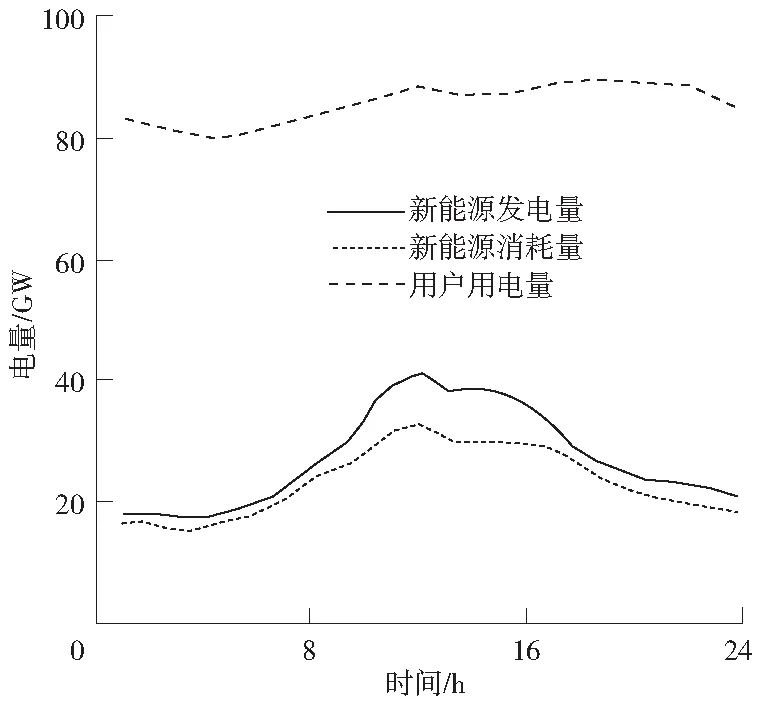
图2 用电量需求和发电量变化曲线Fig.2 Change curve of power consumption demand and power generation
基于表2和图2的数据,代入模型中计算,按照如图3所示的流程图进行分析。如图3所示,仿真计算有以下主要步骤:①数据处理。对某省电网的负荷数据进行整理,得到新能源发电数据、用电数据、负荷数据、初始峰—谷期和电价。②建立目标函数和约束条件。在上述基础上,建立新能源消耗最大化和用户用电满意度最高的目标函数,以及以用电时间和价格为基础的约束条件。③峰—谷优化求解。本文采用粒子群优化算法来获得最佳峰—谷计算结果。④峰—谷电价优化。基于最优峰—谷期,采用粒子群优化算法获得最优峰—谷电价。⑤计算结果对比。通过对比响应前后新增能耗和总电费结果,得到本文模型的计算效果。
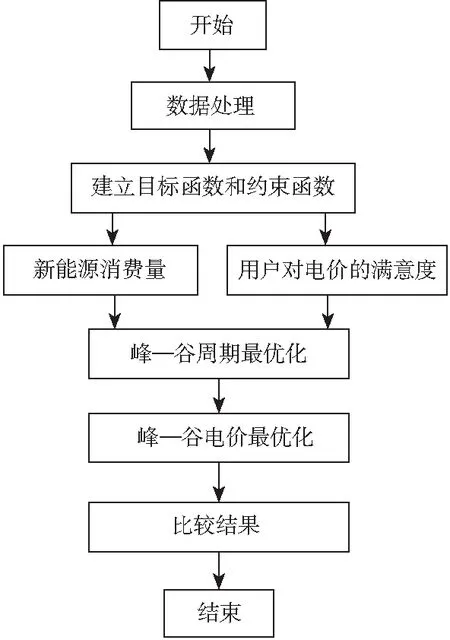
图3 仿真分析流程Fig.3 Simulation analysis process
(2)结果分析。根据模拟过程,峰—谷隶属度阈值为m1=0.68,m2=0.62,用户负荷权重为u1=0.61,u2=0.07,新计算得到的峰—谷期电价为Pf=0.64,Pp=0.46,Pg=0.18,新峰—谷期划分结果见表3,新峰—谷期和电价响应前后的新能耗分布曲线如图4所示。响应前后的新能耗计算结果见表4,新峰—谷期和电价调整前后的新能耗和总电费对比见表5。

表3 新峰—谷期与电价Tab.3 New peak valley period and electricity price
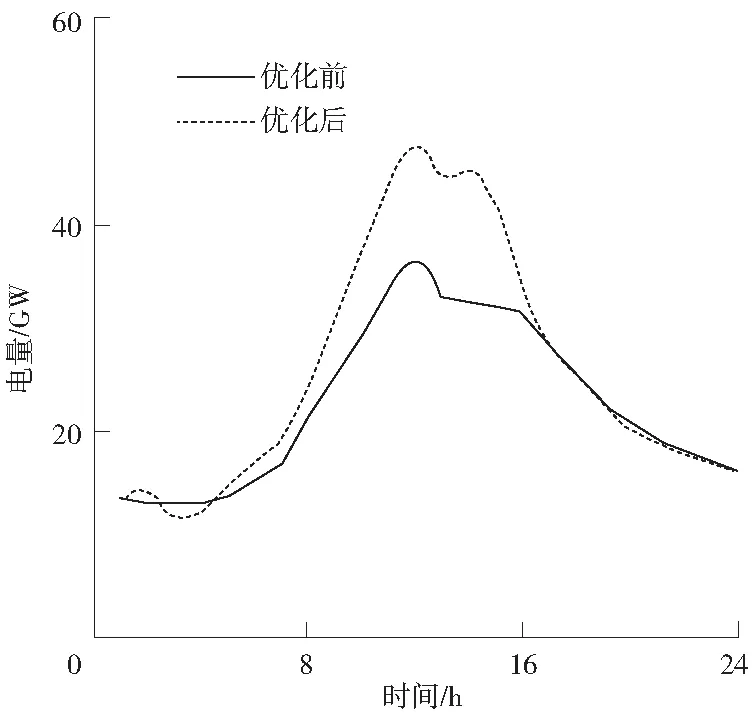
图4 优化前后的新能耗曲线Fig.4 New energy consumption curve before and after optimization

表4 新能源发电与消费、用户负荷统计Tab.4 Statistics of new energy power generation,consumption and user load

表5 新能源消耗与总电费的比较Tab.5 Comparison between new energy consumption and total electricity charge
从图3、表4和表5可以看出,响应新的峰—谷期和电价后,新增能耗从84.32%增加到92.95%,本文提出的优化方法达到了促进新增能耗的目的。
同时总用电成本从849 937.75元降至798 767.55元,提高了用户满意度。
3 结论
本文基于价格弹性理论,考虑峰—谷时段的负荷和新能源产量,提出以能耗最大和用户成本最低为目标函数的峰—谷时段和电价组合优化方法,采用粒子群优化算法求解峰—谷隶属度阈值、用户负荷权重和峰—谷均价,从而促进新能源的消耗。
(1) 采用本文提出的方法,用户响应新的峰—谷时段和电价后,新增能耗从84.32%增加到92.95%,验证了本文方法的有效性。
(2) 用户响应新的峰—谷时段和电价后,总用电成本从849 937.75元降至798 767.55元,降低了6.02%,提高了用户满意度,表明本文提出的方法能够在提高新能源消费的同时提高用户满意度。
