基于模糊数学的二次设备性能评价方法研究及应用

四川蜀能电力有限公司高新分公司 林 波 黄 迎

二次设备性能状态对变电站可靠稳定运行起到至关重要的作用，通过分析二次设备性能评价指标，能为二次设备健康管控、二次系统状态评价提供技术和数据支撑[1]。变电站二次设备测试工作主要对试验数据是否满足规程要求，重点在于测试指标是否合格，未开展对异常或极端运行条件下的参数指标测试；且部分指标测试具有较大离散度，无法通过单次测试获取有效数据。另外，测试数据仅作为各指标结论合格的依据，形成大量数据孤岛，未能系统性综合评价二次设备性能状态[2]。模糊数学最早出现于1965年，由美国控制论专家Zadeh教授提出，它既是一种数学理论，也是一种数学方法，主要对模糊现象进行研究处理。作为一门新兴学科，模糊数学在系统理论、信息检索、医学、生物学等各个领域均有应用[3-5]。本次研究基于模糊数学和测试数据，对变电站二次设备的性能状态建立了一种新的评价方法。

1 变电站二次设备性能评价指标

1.1 构建评价指标体系

在智能变电站中，二次设备种类较多，常见如智能终端、监控后台、以太网交换机、合并单元、测控装置、保护装置、网络报文分析装置等，对这些设备分别构建评价指标体系。本研究以保护装置为例，主要评价指标有接口的性能、保护装置的动作情况、交流量的精度检测等。

1.2 确定评价指标权重

层次分析法（AHP），是决策分析时常用的一种方法，它的特点是将定性分析、定量分析相结合。在分析过程中，因包含了主观性与客观性，判断更具条理化和层次化。本研究基于变权理论下，先建立权重模型，再采用AHP法进行赋权，最后确定各个指标的权重大小。AHP法计算权重的流程见图1。

图1 AHP法计算权重的流程图

2 基于模糊数学的性能评价方法

模糊数学解决的问题，是难以用语言精确描述的，这些问题的共性特点是：①影响因素较多；②具有复杂的结构层次；③指标不易量化。在智能变电站中，二次设备的性能问题就符合这些特点，其一性能指标有多个，其二影响因素也很多，其三定量分析模糊。因此，我们采用模糊数学法，对二次设备性能进行评价，步骤如下。

2.1 建立评估对象的因素集U和评语集V

因素集U是指在模糊综合评估模型中影响评估对象各因素的集合，以U来表示：

评语集V是指所有评估结果的集合，以V来表示：

2.2 建立模糊关系矩阵R

模糊关系矩阵R，是连接因素集U和评语集V的矩阵。分析集U对集V的隶属程度，就能得到模糊关系矩阵R：

式中，元素rij表示因素集U中某个指标Ui对于某类评语Vj的隶属程度。rij值的范围在0-1之间，在此范围内结果越大，说明指标的隶属程度越大，两者的关联性越强。计算隶属度大小，先确定隶属函数，然后计算得到结果。

2.3 计算指标的权重向量W

模糊综合评估是要解决一个由多因素影响的问题，要想提高评估结果的准确性，就必须在指标权重的分配上重点关注，得到指标权重的向量W：

这里选用组合赋权，基于AHP法进行初始赋权，再基于变权理论确定权重。

2.4 选择模糊合成算子

模糊关系合成运算符号M，也就是模糊算子。结合实际情况，评估中常用的模糊算子有：主因素决定型算子M(∧,∨)、主因素突出型算子M(·,∨)、不均衡平均型算子M(∧,⊕)和加权平均型算子M(·,⊕)。四种算子各有优劣，各有长处，需要根据实际情况和需求来选择合适的算子。

在智能变电站中，评估二次设备的性能好坏，理论上应将所有的性能指标包括在内。为了满足这一点，可采用加权平均型算子M(·,⊕)进行评估。

2.5 建立模糊综合评估数学模型

在得到了模糊关系矩阵R和权重向量W之后，建立模糊综合评估数学模型：

其中“°”代表模糊运算符号；B是得到的模糊综合评估结果，表示评估对象对于各个评语的隶属程度。

2.6 得出结论

根据之前的计算得到的模糊综合评估值，来确定对应评估对象的评估等级。

3 基于测试数据的保护装置性能评价应用

本次研究以某220kV变电站的二线保护装置为例，基于真实的测试数据，对其性能进行评价，具体步骤方法如下。

3.1 建立性能评估指标的层次结构模型

根据保护装置的特点以及运行人员的要求，对保护装置的性能评估主要从接口功率、保护装置动作情况、通信异常处理能力、交流量精度检查等方面进行，进一步细分为二级指标。性能评估指标层次结构模型见表1。

表1 性能评估指标层次结构模型

3.2 构造判断矩阵

根据保护装置的运行需求，工作人员对这些需求进行整合分析，从而划分性能指标，得到一级指标的判断矩阵。见表2。

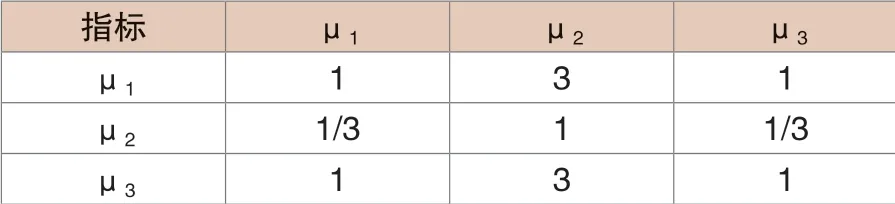
表2 一级指标的判断矩阵

保护装置二级指标相对于一级指标的判断矩阵，见表3-表5。

表3 二级指标中接口性能判断矩阵

表4 二级指标中动作情况性能判断矩阵

表5 二级指标中交流量精度检查性能判断矩阵

3.3 计算各评估指标权值

根据前面提到的权重公式，根据接口功率性中个指标对一级指标的判断矩阵，对二级指标权值进行一一计算，步骤如下。

首先，对判断矩阵进行归一化处理，并且计算行和，得到矩阵见表6。

表6 归一化处理结果

然后对W=(W,W'1,W'2,…,W'n)做归一化处理。

3.4 确定需要变权的指标

要想得到一级指标的评估结果，首先要对二级指标进行评估。对此，改变常规工作方法，一级指标不需要变权处理，而是根据评估工作的需要，选择一些特殊的性能指标（超过或低于预设值），计算该指标的权重。再根据指标性能的判断方法，以及工作人员的过往经验，对限值进行计算和设定。其中，定性指标可通过评测人员根据测试结果的优劣情况，以百分制的形式对这些指标结果进行量化，分数越大越好。用某一次性能测试结果得到指标参数见表7。

表7 根据性能测试结果得到指标参数

纵联差动分数与零序方向过流保护分数计算方式为：

式中Y表示评价分数，t表示实际保护出口时间，t0表示标准值，220kV纵联差动保护出口时间规定不能大于30ms。零序方向过流保护出口时间不大于30ms。

电流量、电压量精度评价的计算方式为：

式中φ为精度百分比，1为实际测量值，I0为标准值。

3.5 变权计算

根据计算公式和表中数据，计算出各性能指标的状态变权S，再根据初始权重计算变权重，结果如下：

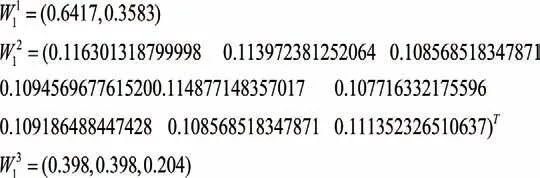
3.6 建立因素集U、评价集V与模糊关系矩阵R

评价保护装置的性能时，一级指标有三个，二级指标则是一级指标的子集。因此，评估的因素集为：

U=(u1,u2,u3)

因素集的评估子集为：

u1=(u11,u12)

u2=(u21,u22,u23,u24,u25,u26,u27,u28,u29)

u3=(u31,u32,u33)

对于保护装置的模糊综合评价，采用“优”“良”“一般”三个指标。如果是越小越优，那么μmin、μmax、μ0分别代表优、一般、良；如果是越大越优，那么μmin、μmax、μ0分别代表一般、优、良。因此评估语集为：

V=(v1,v2,v3)

确定隶属函数式中的未知参数，μmin、μmax、μ0可以根据前面指标参数以及专家意见给出(μ0通常为最大最小平均值)。将其带入隶属函数公式，得到模糊关系矩阵：

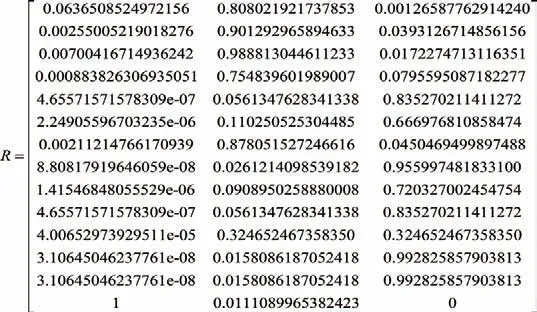
选择采用加权平均型算子M，对智能变电站二次设备进行性能评估，接口性能的模糊综合评价结果为：

最终评价结果：

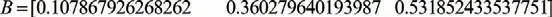
3.7 得出评价结果

通过上述模糊综合评价计算，得出该保护装置性能的模糊综合评价结果，评价标准：一般0.11，良0.36，优0.53。根据上表结果和按照模糊综合评估的最大隶属度原则，可得到该保护装置的评价等级为优。

4 结语

综上所述，本文基于现有评价技术的研究与电网健康评价与管控的需要，以及目前在测试工作后仅做出功能性结果评价的片面性，提出了基于测试数据、适用于现场的测试对象性能评价方法。结果证实：基于模糊数学的二次设备性能评价方法具有可行性，能够帮助测试人员对智能变电站二次设备状态有更加直观与准确的认识，有利于得出正确的测试结果评价，保障智能变电站安全可靠运行。另外，项目提出的基于测试数据的性能评价方法，可为日后二次系统状态检修、二次设备监控评价与管控等相关工作提供理论支持。在未来，随着模糊数学理论和实践的研究深入进行，未来应用领域会更加广泛，为设备性能评价、运维管理提供一种新方式，具有良好的应用前景。