高中数学深度学习教学策略的研究

梁敏聪

（广州市南沙东涌中学，广东 广州）

在日常教学活动中，教师应重视深度学习，培养学生的高阶思维。合理的问题引领，有利于带动学生深度思考；适当的优化整合，有利于促进学生知识网络的建构；多维的评价角度，有利于培养学生学习的兴趣。

随着“新课标、新课程、新教材”改革的不断推进，教师的教学也要适应新形势的发展，传统的“填鸭式”教学已经过时了，教师不仅要对新教材进行深入的研究，还要思考如何促进学生学习的真实发生。教师是教学活动的“引路者”，要带动学生积极参与课堂活动，体验成功。随着教学改革的深入发展，素质教育提出了深度学习这一教学要求。

一、深度学习的内涵

深度学习就是指在教师引领下，学生围绕具有挑战性的学习主题，全身心积极参与、体验成功、获得发展的有意义的学习过程。

深度学习强调学生立场，关注学习的真实发生，关注学生在教学中的主体地位，集中表现在主动参与、积极体验、深入思考。

二、促进学生深度学习的教学策略

深度学习通过学生主动参与课堂活动，自主获取知识。它不是被动的、机械的，而是一种主动的学习。教师应思考如何促进学生的深度学习。

（一）问题策略：合理的问题引领，有利于带动学生深度思考

深度学习需要问题引领。这个问题引领，不仅是指问题情境的引入，还包括探究活动的全过程、学习反思等，它会贯穿整节课。

1.创设问题情境，激发学生内在学习动机

上概念课的时候，个别教师把教材上讲概念时的问题情境弃之不用（直接抛出概念），或者只使用部分，又或者用自己在其他地方找的，但又不很恰当的问题情境。他们认为，问题情境引入会耽误课堂时间，后面的题就讲不了了，这节课的教学任务就完不成了。其实，抱有这种想法是不对的。作为一线教师，我们应该明白，概念课必须让学生充分地经历概念的抽象过程，更好地理解概念。只有把概念、原理讲透、讲深，那反过来用概念、原理去解决问题才能迎刃而解。不能只是为了讲题，为了讲题，就成了习题课了。我们常常为学生对概念认识不清晰而感到叹息，我们需要反思：当时上概念课时，是否讲到位了，是否有让学生充分经历概念抽象的深度思考过程。

例如，讲到函数的概念这一节时，通过引入问题情境，再对其进行深挖，激发学生内在学习动机。

情境：高速列车加速到400 km/h 后，仍然保持匀速前进0.4 小时。

问题1:在这0.4 小时内，车前进的路程S 与运行时间t 之间的关系式是什么？这是一个函数吗？为什么？

问题2：“如果对应关系是S=400 t，则车加速到400 km/h 后，运行1 小时就前进了400 千米。”这种说法对吗？

问题3:你认为该如何表述S 与t 的对应关系？

通过设置层层递进的问题串，让学生自主发现其中的不严谨，为由初中已有的函数概念过渡到用集合的语言精确刻画函数概念做好准备。

2.问题引领活动，引导学生探究

除了在课堂引入方面创设问题情境，还可以在具有挑战性学习主题活动中巧设问题串，引导学生探究。但有时候生源不同，学生的探索能力就有所不同，如果仅仅只是抛出一个学习主题活动，让学生自由探究，估计有部分学生会很迷茫，这个时候就需要问题的引领，带动学生去探究。

在学习直线与平面垂直的判定定理时，可以尝试这样处理：

首先提出疑问：如果要证明线面垂直，由定义可知，必须证明一条直线与平面内任一条直线都垂直。这确实很难操作。还有其他方法能证明线面垂直吗？

回忆线面平行的判定定理：可由一次的线线平行推出线面平行。

能否同样由线线垂直推出线面垂直问题？

探究1 平面外一条直线和平面内一条直线垂直，能保证该直线垂直于这个平面吗？若不能，请举出反例。

探究2 一次线线垂直不行，两次线线垂直行不行呢？

①如果平面外一条直线分别与平面内两条平行直线都垂直，则该直线垂直于此平面吗？

②如果平面外一条直线分别与平面内的两条相交直线都垂直，则该直线垂直于此平面吗？

探究3 利用手上的一张三角形纸片，动手操作：过△ABC 顶点C 折叠这张纸片，得到折痕CE，将折叠后的纸片竖起放置在桌面上（使AE、EB 都与桌面接触）。

追问（1）：CE 与桌面垂直吗？

追问（2）：如何折叠才能使CE 与桌面垂直？

对这个定理，教材是不需要证明的，而是通过直观感知，动手操作，思辨归纳出来的，培养学生的直观想象素养。设置以问题为驱动的探究活动，可以让学生亲身经历定理的抽象形成过程，让学生对这个定理理解得更加透彻，培养学生的数学核心素养。

3.层层追问，引起学生的反思

在教学过程中，教师要善于运用深度追问的策略引起学生的反思，推进深度学习。

例如，在直线与平面垂直这节课的最后，我们可以启发学生进行小结：本节课你学到了哪些知识？又是用怎样的方法学到这些知识的？直线与平面平行的判定定理和直线与平面垂直的判定定理最大的不同点是什么？今天学到了什么数学思想？

通过一系列的追问，带动学生梳理本节课所学的知识，并回顾本节课的学习过程，让学生在更大的范围内将所学的知识进行优化和整合。

除了在反思中进行追问，也可以进行纠错追问，将错误淋漓尽致地摆在学生面前，让学生一起来纠错。只有准确地把握导致错误的症结，才能使错误得以增值，使课堂变得高效。

总之，问题是数学学习的起点，也是数学学习的动力。在教学中，教师设置层层问题，引导学生进行深入的思考。在问题的驱动下，让教师引在关键处，让学生主动经历概念、原理的抽象过程，使活动真实地发生，才能培养学生的数学核心素养。

（二）整合策略：适当地优化整合，有利于促进学生知识网络的建构

深度学习对教师、学生都是新的挑战，它要求教师认真研读教材、教师用书，对整章书的教学内容、学习目标、重难点进行整体的规划，使用单元整体设计时，既要考虑整体又要兼顾到每一课时。教师需要理清知识框架，将新授知识与前后知识形成横向和纵向的联系，建立知识网络，把握知识间的内在逻辑关系。在课堂上，要帮助学生完成深度学习的关联整合。在平时授课中，要注重引导学生发现数学知识间的关联，让学生将头脑里碎片化、零散的数学知识理清，让学生的数学学习条理化、系统化，完成对数学学习的建构过程。其中，最好的做法是让学生自己去画思维导图。

例如，在高一学习“立体几何初步”的八大定理后，我发现学生对定理的记忆很混乱。于是，我引导学生结合思维导图，将八大定理及相关性质串在一起记忆，包括证明线线平行、线线垂直的证明方法。图形语言、符号语言，再标上定理所需要的条件个数，那就更完美了，如图1、图2。通过绘制思维导图，既规范了证明格式，又整合了整章知识，让学生把握知识的本质和关联，真正实现深度学习。适当地优化整合，有利于促进学生知识网络的建构。

图1

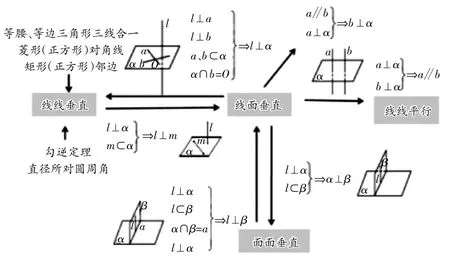
图2

（三）评价策略：多维的评价角度，有利于培养学生学习的兴趣

深度学习的顺利开展，还要依赖于评价。由于深度学习强调的是学生积极参与学习的过程，因此评价的手段、方法对提高学生的积极性起着很重要的作用。教师通过引入多维的评价角度来开展合理、有效的评价。例如，在学生探究活动中，可以使用课堂观察量表对学生的上课表现、回答问题、小组合作、交流讨论等方面进行评价。教师要关注学生在学习过程中学习态度的变化，以及关注学生数学核心素养的养成。

数学深度学习需要教师精心设计与科学引导，让学生的学习更深入、更清晰、更合理。面对新课标、新课程、新教材，教师应该自觉地将深度学习逐渐融入高中数学课堂，激发学生的学习兴趣，发展学生的高阶思维，培养学生的数学核心素养。