基于时间顺序脉冲神经膜系统的电网故障诊断方法

林德垠

（西华大学电气与电子信息学院，四川 成都 610039）

0 引言

随着电网规模不断地扩大，故障的复杂性也不断增加，利用故障数据进行电网故障诊断可以快速、准确地找出故障区域或故障设备，对迅速恢复供电具有重要意义。近年来，在电网智能故障诊断的研究课题中，许多国内外专家与学者相继提出多种故障诊断方法，例如专家系统、人工神经网络、Petri网、解析模型和脉冲神经膜系统等。目前，基于脉冲神经膜系统（Spiking Neural P System，SNPS）的故障诊断方法凭借其逻辑清晰严密、推理过程简单明了的优势受到广泛关注。

警报信息中的时间属性是电网发生故障时的一个重要特征，其包括丰富的故障相关信息，如何利用警报信息中的时间属性对研究电网故障诊断具有重要意义。文献[6]将溯因推理应用在电网故障诊断中，解释了发生故障的原因，并且还原了发生故障的过程。文献[7]提出了一种基于时间序列相似性匹配的电力系故障诊断方法，该方法利用警报假说时间序列与实际警报时间序列之间的距离来识别故障元件与故障类型。文献[8]利用保护装置的时间关联特性将时间模糊Petri网运用到电网故障诊断中。文献[9]为了充分利用警报信息的时序特性，提出了一种时态模糊推理实数脉冲神经网络系统。文献[10]将警报信息中保护装置动作的因果关系与脉冲神经膜系统结合起来，提高了故障诊断过程中处理警报信息不确定性的能力。

脉冲神经膜系统是膜计算领域的一个重要分支，它是受生物神经元通过脉冲形式存储、传递和交换信息启发而提出的一类特殊神经膜系统。SNPS的图形化诊断模型不仅可以直观、形象地表达、推理故障知识，而且其强大的分布式并行计算能力能够有效地处理故障警报信息的不确定性。然而，SNPS在电网故障诊断过程中处理时序信息的能力还较为薄弱，没有充分利用警报信息的时间属性以及信息之间的时间约束特性。因此，该文在脉冲神经膜系统的基础上，利用警报信息中断路器、继电器动作的时间属性以及保护装置之间的动作顺序和时序约束关系建立基于时间顺序实数脉冲神经膜系统（Time Sequence Spiking Neural P System with Real Numbers，rTSSNPS）的故障诊断模型。同时，为了简化对警报信息进行时序处理的过程，该文结合故障诊断模型重新设置推理算法，使算法具有处理警报信息时间属性的能力，从而提升脉冲神经膜系统处理保护装置拒动、误动、时标错误和信息丢失等不确定性的能力，进而减少运算步骤，提高故障诊断效率。

1 rTSSNPS

1.1 rTSSNPS定义

可以将1个rTSSNPS定义为多元组，如公式（1）所示。

σ为命题神经元集合，σ=（θ,T,λ,r,w）（1）（为命题神经元的个数）；σ为规则神经元集合，σ=（θ,c,T,λ,r,w）（1）（为规则神经元的个数）。其中，θ为第个命题神经元内部脉冲的脉冲值，θ为[0，1]的实数；θ为第个规则神经元内部脉冲的脉冲值，θ为[0，1]的实数；T为命题神经元的时间信息脉冲，每个命题神经元都会产生1个时间信息；T为各个命题神经元之间的时间距离，表示上个命题神经元点火到下个命题神经元激发的时间距离约束；r为命题神经元σ的点火规则，其形式为/α→α（为点火条件；为神经元；为传递的脉冲），和为[0，1]的实数；r为规则神经元σ的点火规则，其形式为/α→α（为产生的新脉冲），和为[0，1]的实数；λ和λ分别为命题神经元和规则神经元的点火阀值，它们都是[0，1]的实数；w和w分别为命题神经元σ的输出权重向量和规则神经元σ的输出权重向量；c为规则神经元的真值，c为[0，1]的实数，与σ对应的模糊产生式规则的确定性因子相等。该脉冲神经膜系统涉及4种类型的神经元，即一类命题神经元（用符号“”表示）和三类规则神经元，即“常规”“与”和“或”规则神经元，分别用字母“general”“and”和“or”来表示。

1.2 模糊产生式规则

类型一（常规规则）为（-c）：IFp（θ，T，T，w）THENp（θ，T），相应的rTSSNPS模型如图1（a）所示。其中，p与p分别为规则R的前件命题与后件命题；c为规则R的确定因子，c为[0，1]的实数；θ和θ分别为命题p和p产生的真值，θ和θ为[0，1]的实数；T、T分别为完成命题p和命题p所消耗的时间，也可以表示命题神经元σ和命题神经元σ点火的时间点；T为命题p到命题p所消耗的时间，也可以表示命题神经元σ到命题神经元σ的时间距离；w为命题p的权重值。

命题p的真值和时间如公式（2）~公式（3）所示。

其运算符号的解释如公式（4）所示。

式中：为（）维度的逻辑矩阵；、为的时间矩阵；和分别为时间矩阵和中的时间元素；A为矩阵中的逻辑元素；、为该矩阵的行和列。

类型二 （复合“与”规则）为（=c）：IF（，，T，）and…andp（θ，T，T，w）THENp（θ，T），相应的rTSSNPS如图1（b）所示。其中，，…，p为规则R的前件命题；p为规则R的后件命题；c为规则R的确定性因子，c为[0，1]的实数；，…，θ分别为，…，p的真值，，…，θ为[0，1]的实数；θ为命题p的真值，θ为[0，1]的实数；，…，T分别为完成命题，…，p所消耗的时间，也可以分别表示命题神经元，…，σ点火的时间点；T=[T，…，T]分别为命题，…，p到命题p所消耗的时间，也可以分别表示命题神经元，…，σ到命题神经元σ的时间距离；，…，w分别为命题，…，p的权重值。

命题p的真值和时间如公式（5）~公式（6）所示。

类型三（复合“或”）为（-c）：IF（，，T，）or …orp（θ，T，T，w）THENp（θ，T），相应的rTSSNPS如图1（c）所示。其中，，…，p为规则R的前件命题；p为规则R的后件命题；c为规则R的确定因子，c为[0，1]的实数；，…，θ分别为命题，…，p的真值，，…，θ为[0，1]的实数；θ为命题p的真值，θ为[0，1]的实数；，…，T分别为完成命题，…，p所消耗的时间，也可以分别表示命题神经元，…，σ点火的时间点；T=[T，…，T]分别为命题，…，p到命题p所消耗的时间，也可以分别表示命题神经元，…，σ到命题神经元σ的时间距离；，…，w分别为命题，…，p的权重值。

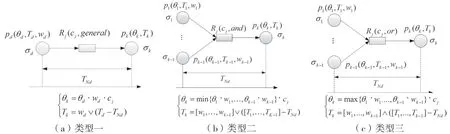
图1 rTSSNPS 3种模糊产生式规则

命题p的真值和时间如公式（7）~公式（8）所示。

其运算符号的解释如公式（9）所示。

式中：、为×的实数矩阵；、为×的时间矩阵；为×的逻辑矩阵；max为最大值，、为该矩阵的行和列。

1.3 时间脉冲矩阵推理算法

为了能使算法准确、高效地表达和推力知识，减少运算的复杂程度，更加契合故障诊断过程中保护装置动作的逻辑关系，该文根据线路和母线的故障诊断模型将推理算法分为算法一和算法二。其中，算法一完成线路送端与受端双向并行矩阵推理运算以及母线各个出线方向多向并行矩阵推理运算任务；算法二综合线路送端与受端、母线各个出线方向输出结果对故障元件进行识别。时序脉冲矩阵推理算法如下。

算法一如下。

输入：W，W，T，，λ，λ，，，，

输出：神经元的时间与真值

令推理步骤=0

根据输入的初始条件计算根据、、、计算

则推理步数=+1

While （<3）do

for 每个命题神经元 do

if 点火规则={α，θ≥λ，1}满足，then该命题神经元点火并根据公式

计算和

if 命题神经元存在突触后规则神经元 then 该命题神经元向其突触后规则神经元发送1个脉冲和时间

else 该命题神经元仅积累脉冲和时间

for 每个规则神经元do

if 点火规则={α，δ≥λ，1}满足，

then 该神经元点火并根据公式

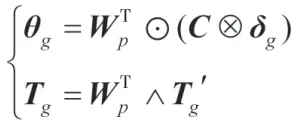
计算θ与，并向其突触后命题神经元发送1个脉冲与时间

其中，θ=[,…,θ]为命题神经元的实数脉冲值矩阵θ（=1,…,） 为[0，1]的实数，表示第个命题神经元的脉冲值；δ=[,…,δ]为规则神经元的实数脉冲值矩阵，δ（=1,…,）为[0，1]的实数，表示第个规则神经元的脉冲值；=（,…,c）为规则神经元的对角矩阵，c（=1,…,） 为[0，1]的实数，表示第个规则神经元的真值；T=[,…,t]为当前所在推理步骤命题神经元的时间矩阵，该矩阵包括个命题神经元的动作时间，t（=1,…,）为时间信息，表示第个命题神经元点火的时间；T=[t,…,t]为规则神经元的时间距离矩阵，t（=1,…,）时间常量，表示规则神经元前件命题神经元的点火到规则神经元后件命题神经元激发时消耗的时间；W为规则神经元到命题神经元的突触权重矩阵；W、W、W分别为命题神经元到“常规”规则神经元、“与”规则神经元以及“或”规则神经元的突触权重矩阵；λ=[λ,…,λ]为命题神经元的点火阀值矩阵，λ（=1,…,） 为[0，1]的实数，表示第个命题神经元的点火阀值）；λ=[λ,…,λ]为规则神经元的点火阀值矩阵，λ（=1,…,）为[0，1]的实数，表示第个命题神经元的点火阀值。

算法二如下。

输入：W,W,T,,,

输出：神经元时间与真值

综合算法一的输出结果令推理步骤=3，计算

输出：θ=[θ+（T）]/2和T

如果给出rTSSNPS中输入神经元的初始脉冲值、时间点约束矩阵以及各个命题神经元之间的时间距离约束矩阵，那么该系统通过执行算法一和算法二就能够获得其余命题神经元的真值与时间点约束区间。θ=[，…，θ]为命题神经元的实数脉冲值矩阵，θ（=1，…，）为[0，1]的实数；δ=[，…，δ]为规则神经元的实数脉冲值矩阵；δ（=1，…，）为第个规则神经元的脉冲值，δ（=1，…，）为[0，1]的实数；=diag（，…，c）为规则神经元的对角矩阵；c（=1，…，）为第个规则神经元的真值，c（=1，…，）为[0，1]的实数；T=[，…，t]为当前所在推理步骤命题神经元的时间矩阵，该矩阵包括个命题神经元的动作时间；t（=1，…，）为时间信息（第个命题神经元点火的时间）；T=[t，…，t]T为规则神经元的时间距离矩阵；t（=1，…，）为时间常量（规则神经元前件命题神经元点火到规则神经元后件命题神经元激发时消耗的时间）；W为规则神经元到命题神经元的突触权重矩阵（如果规则神经元σ到命题神经元σ存在突触，则w∈（0，1]，其等于突触（，）的输出权重，否则w=0；W，W，W分别为命题神经元到“常规”规则神经元、“与”规则神经元以及“或”规则神经元的突触权重矩阵（如果命题神经元σ到规则神经元σ存在突触，则w∈（0，1]，其等于突触（，）的输出权重，否则w=0；λ=（λ，…，λ）为命题神经元的点火阀值矩阵；λ（=1，…，）为第个命题神经元的点火阀值，λ（=1，…，）为[0，1]的实数；λ=（λ，…，λ）为规则神经元的点火阀值矩阵；λ（=1，…，）为第个命题神经元的点火阀值，λ（=1，…，）为[0，1]的实数。

在该算法中，各个乘法算子定义如公式（10）所示。

式中：为×的实数矩阵；、为×的时间矩阵；为一种运算推理过程。

对故障诊断模型来说，已知原因事件实际动作时间（t）及通过时间推理得到的原因事件的动作时间（t），利用公式（10）判断推理过程是否准确，如公式（11）所示。

式中：为×的实数矩阵；为×的时间矩阵；为一种运算推理过程。

对故障诊断模型来说，利用公式（11）检查事件经过时序信息处理是否因故障而动作，如公式（12）~公式（13）所示。

式中：、为×的实数矩阵；为×的逻辑矩阵；avg为数值取平均数。

式中：为×的实数矩阵；为×的逻辑矩阵；plus为数值相加。

2 基于rTSSNPS的电网故障诊断模型

该文简化利用时序信息的过程，将保护装置动作的时间属性融入故障诊断模型中，使神经元不仅能够传递脉冲值，而且能够传递时间信号；同时，通过建立诊断模型增强拓扑结构的适应能力，降低计算的复杂程度，提高了故障诊断的效率。

2.1 利用时序信息

当电网发生故障时，保护装置动作有严密的逻辑关系，以线路或母线故障为起点，保护装置动作的先后顺序如下：主保护继电器及其对应的断路器动作，近后备保护继电器及其对应断路器动作，远后备保护继电器及其对应断路器动作。主保护、近后备保护和远后备保护动作的时间约束分别为10 ms~40 ms、310 ms~340 ms和450 ms~510 ms，断路器到各相应保护继电器的时间约束为20 ms~60 ms。

结合rTSSNPS故障诊断模型，为了简化处理警报信息中时间信息的过程，根据文献[11]并利用t及其对应时间距离约束（t，t）得到该事件的前驱事件以及前驱事件的时间约束，如公式（15）所示。式中：（t）为该事件的前驱事件的时间约束；（t）为该事件的时间约束。

2.2 故障诊断模型

以IEEE39节点系统为例，建立线路L诊断模型（图2）。该文根据保护装置动作时间先后的逻辑关系建立故障诊断模型（当诊断电网故障时，根据从元件故障到继电器动作再到断路器跳闸的动作顺序和时间约束建立诊断模型），每个命题神经元都会被赋予1个脉冲值和1个时间点约束。其中，脉冲值表征该命题神经元的置信度，时间点约束表征该命题神经元点火的时间约束。此外，命题神经元之间都会有1个时间区间约束，表征从上一个命题神经元点火到下一个命题神经元激发所消耗的时间。

图2 线路L0414的rTSSNPS的故障诊断模型

为了更直接、更清晰地将警报信息展示在建立的诊断模型中，用~表示警报信息中保护装置的动作时间，用（t，t）、（t，t）等表示保护装置之间的时间约束。与文献[10]不同，该文提出的故障诊断模型直接将警报信息的时间点约束矩阵、保护装置之间的时间距离约束矩阵和保护装置的初始置信度作为输入，将元件故障概率和故障约束时间作为输出，简化处理警报信息中时间信息的过程，从而提高故障诊断的效率。

同时，该文为了使诊断模型适应电网拓扑结构的变化，根据动作时间的先后逻辑建立故障元件的诊断模型。当线路发生故障时，在线路的送端与受端分别建立主保护子网、近后备保护子网以及远后备保护子网；当母线发生故障时，在母线的出线方向分别建立主保护子网、远后备保护子网。当拓扑结构发生变化时，线路故障诊断模型只需要增加或减少远后备保护及其对应的断路器，母线故障诊断模型只需要增加或减少出线方向的诊断子网络， 保证故障诊断模型拓扑结构、突触连接矩阵、输入矩阵及输出矩阵的变动较小。

2.3 诊断方法流程图

基于rTSSNPS的故障诊断方法的具体操作流程，如图3所示。

图3 故障诊断流程图

步骤一：确定故障区域中的可疑元件集={，，…x}。在SCADA系统中读取有关保护装置的动作信息，利用结线分析法判断停电区域中的可疑故障元件集。

步骤二：建立故障诊断模型。利用保护装置逻辑动作规则和警报信息的时间信息分别针对各个可疑故障元件x建立基于rTSSNPS的故障诊断模型。

步骤三：获取输入神经元脉冲值和时间矩阵。根据表1 和表2的保护装置动作的可信度与保护装置为未动作的可信度，并结合实际动作信息赋予输入神经元脉冲值，利用警报信息的时间信息赋予并确定输入神经元的时间矩阵，再根据保护动作逻辑规则确定各命题神经元之间的时间距离矩阵。

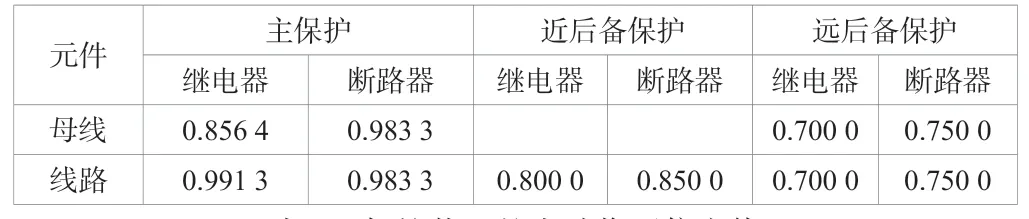
表1 保护装置的动作可信度值

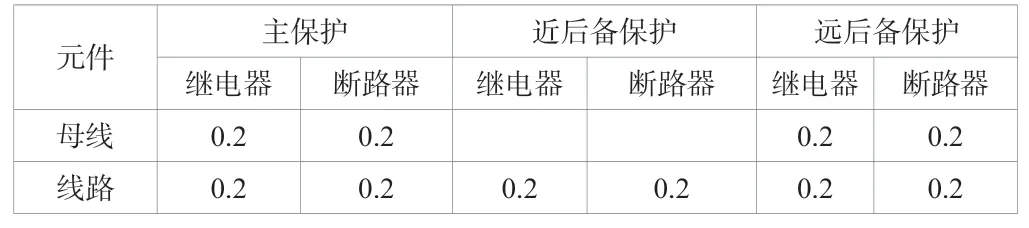
表2 保护装置的未动作可信度值

步骤四：判断故障元件。对故障区域中的各个可疑元件x执行时间脉冲矩阵推理算法，并计算输出神经元的时间点约束区间及其脉冲值。其中，设置输出神经元的故障阀值为0.5，判定数值大于0.5的元件为故障元件，否则无故障元件。

步骤五：输出诊断结果。将步骤四推理得到故障元件及相关时间区间与警报信息进行对比，判断保护装置是否存在拒动、误动以及漏报等情况。

3 算例分析

基于IEEE39节点系统模拟不同场景下的电网故障诊断过程，以验证该文提出的模型的有效性和容错性。这些场景包括状态信息不完整和不确定的复杂故障，警报信息见表3。将该文提出的方法与文献[10]、文献[12]中的2种经典故障诊断方法进行对比，结果见表4。同时，将该方法与近年来提出的故障诊断方法进行对比分析，结果见表5。

表3 保护装置故障信息

表4 算例识别结果与比较

表5 该文所采用的方法与现有3种方法的对比

表4中算例一~算例二为单一故障，算例三~算例六为多重故障。对算例一、算例三、算例五和算例六来说，3种方法都能准确识别故障元件，然而文献[12]未能明确不同故障元件的时间点约束与时间区间约束的关联属性，其在算例二中错误诊断母线B发生故障，在算例四中错误诊断L发生故障。从表5中可以看出，文献[3]不能识别时序错误的动作信息，而文献[10]与文献[12]虽然能够正确地对保护装置进行评价，但是由于2种方法都需要先对警报信息进行时序处理，因此诊断速度较慢。

对表4与表5进行分析可知，该文提出的故障诊断方法，充分利用警报信息中保护装置的时序信息以及保护装置之间的时序约束关系，并将其在建立的诊断模型上直观地表现出来，实现了时序信息与故障置信度的并行推理，能够快速处理继电器/断路器拒动、误动以及警报信息缺失等复杂情况，进而准确识别故障元件，提高故障诊断的效率，具有较高的容错性（以算例二和算例三为例进行详细说明）。

算例二：单重故障。在发生故障后，调度中心收到的警告信息为B（31 ms）、L（27 ms）、L（32 ms）、L（472 ms）、L（466 ms）、CB（73 ms）、CB（504 ms）以及CB（516 ms）。采用基于rTSSNPS的故障识别方法对该案例进行故障诊断的流程如下。

步骤一：确定故障区域可疑元件集。根据警报信息利用结线分析法搜索故障区域得到可疑故障元件集={B，L，B}。

步骤二：建立故障诊断模型。根据可疑故障元件集={B，L，B}分别针对线路L、母线B和母线B建立基于rTSSNPS的故障诊断模型（由于篇幅有限，算例二以线路L为例进行详细说明，其故障诊断模型如图2所示）。

步骤三：获取输入神经元脉冲值和时间矩阵。该文以线路L送端诊断模型为例进行推理说明，输入神经元脉冲值和时间矩阵分别如公式（16）~公式（20）所示。

式中：为零矩阵（不同下角标对应不同的运算规则）；∅为警报信息未包括该保护装置动作的时间信息。

相关突出权重矩阵如公式（21）所示。

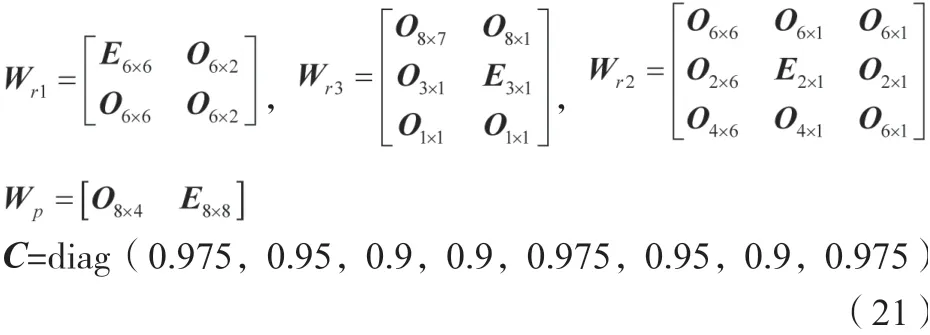
步骤四：判断故障元件。线路L送端诊断模型执行时间脉冲矩阵推理算法，当=0时，推理得到的结果如公式（22）所示。

当=1时，推理得到的结果如公式（23）所示。

当=2时，推理得到的结果如公式（24）所示。

同理，可以得到其受端诊断模型的输出脉冲值与时间点约束分别为0.694 7和-38 ms~16 ms，则执行时序脉冲矩阵推理算法二得到输出结果为0.897 2和-13 ms~16 ms。因此，判断线路L为故障元件，其故障概率为0.8972，故障时刻为-13 ms~16 ms。类似的利用相关报警信息构建母线B和B的rTSSNPS故障诊断模型，2条母线故障概率分别为0.267 4和0.100 4。

步骤五：输出诊断结果。根据步骤四对故障元件的判断并结合SCADA系统中获得的警报信息可以推出线路L在-13 ms~16 ms时刻发生故障。其中，在线路L发生故障后，线路两端主保护正确动作，送端断路器CB跳闸，但是线路受端CB拒动，由线路受端远后备保护L、L动作跳开两端断路器CB、CB，而B误动，B无故障。

算例三：多重故障。故障发生后调度中心收到的警告信息为B（25 ms）、L（27 ms）、L（32 ms）、L（475 ms）、CB（52 ms）、CB（65 ms）、CB（65 ms）、CB（65 ms）以及CB（521 ms）。

算例三的诊断过程与算例二相同，首先，确定故障区域可疑元件集={L，B，L，L}。其次，分别建立可疑元件的故障诊断模型，并根据警报信息获取输入神经元脉冲值与时间矩阵，根据矩阵推理算法得到可疑故障元件的故障置信度和时间点约束分别为（L，0.9557，（-8 ms~17 ms））、（B，0.9028，（-11 ms~15 ms））、（L，0.1200，∅）以及（L，0.1343，∅）。最后，根据故障元件的判断以及相关警报信息可知，线路L在-8 ms~17 ms时间段发生故障，线路两端主保护正确动作并作用于相应断路器跳闸；母线B在-11 ms~15 ms时间段发生故障，母线B的L和L出线方向主保护正确动作跳开相应的断路器，但是母线B的L出线方向断路器CB拒动，其远后备保护L动作跳开断路器CB，线路L、L无故障。

4 结论

该文提出了一种改进的时间顺序实数脉冲神经膜系统电网故障诊断模型和算法，根据警报信息的时间属性与保护装置之间的时序约束逻辑关系建立故障诊断模型， 减少其拓扑结构随着网络变化的调整幅度；将继电器和断路器的初始置信度和其动作时间作为时序脉冲矩阵推理算法的输入，将元件故障概率和元件故障约束时间区间作为输出，省去保护装置时序约束一致性判断步骤；将时间脉冲矩阵推理算法与rTTSNPS故障诊断模型相结合，实现并行推理运算，减少了计算的复杂程度。该方法充分运用保护装置动作的时间逻辑关系，简化时序推理过程，拓扑结构适应性强， 可以提高故障诊断效率，还可以处理警报信息缺失、时标错误，保护装置拒动误动等问题。