全回转重吊船关键区域多体动力耦合优化设计

孟 珣，唐 品，2，邓兴旗，生训宁，李德江，3*

(1.中国海洋大学 工程学院，山东 青岛 266100;2.中国电建集团华东勘测设计研究院有限公司，浙江 杭州 311122;3.烟台中集来福士海洋工程有限公司，山东 烟台 264035)

21世纪，人类进入全面开发利用海洋的新时代。在港口码头、跨海桥梁、海上油气田、海上风电场、海上机场及海底管网等众多工程，尤其在深远海工程建设中，越来越多地开始使用主体结构为浮基的大型起重船。相比于陆地作业，海上重吊施工生产投入高、风险系数大且技术要求强，服役重吊船除了承受海洋环境载荷激励外，施工作业中特定操作工况下吊装组块的质量及转动惯量动力影响也很大，上部机构的耦合运动会引起整个多体系统复杂的动力响应，带来安全隐患。深刻理解环境场特征和多体系统耦合机制，对海工装备的科学设计、安全施工与经济运维至关重要。

早期，多体动力学的研究多集中于航天领域[1]。自20世纪60年代至今，已经形成了许多各具特色的方法，如Newton-Euler[2]、Lagrange[3]、Roberson-Wittenburg[4]、Kane[5]和Huston[6]方法等。随着人类开发利用海洋资源活动的日益活跃，海洋工程装备的数量不断增多，其结构形式也日趋复杂。20世纪90年代，采用多体动力学理论解释海洋工程复杂系统子结构之间的耦合规律成为研究热点。Mohammad和Yoshiyuki[7]采用多刚体理论分析了连续离散浮筒式浮桥在波浪中的运动响应;Chen等[8]、Chen和Fang[9]将频时域混合法用于多浮体系统的分析，其浮体间连接简化为柔性弹簧;Sun等[10-11]通过拉格朗日乘子方法建立了系统的多体耦合运动方程;勾莹等[12]利用牛顿第二定律将浮体之间的约束作用表达成约束力和约束力矩，引入位移连续条件，直接联立求解耦合运动方程。这些研究多针对海洋工程中多个浮体与流场的耦合运动方程高效求解及与之相关的多体间连接假定，并未考虑多体系统内浮基上部组块在运动时动力学参数变化，如质量、转动惯量、加速度等对整体系统的影响，而事实上这种影响往往是不可忽略的。

海上重吊船主要用于重物的装卸、转移和运输等工作。随着单件货物或结构物越来越重型化，重物与重吊船之间的动力与运动耦合变得更为复杂。Kral等[13]、Kral和Kreuzer[14]以起重船为研究对象给出了典型浮基多体系统运动特性。Patel等[15]采用数值模型分析了吊物系统与船体的耦合作用。Nojiri和Sasaki[16]研究了外部激励与吊物系统共振问题。杨宝林[17]分析了起重机启动、制动下臂架的受力变化及起重机变幅和回转作业时吊物的摆动规律。王学林等[18]研究了规则波作用下船体和吊物的运动响应。沈庆等[19]采用多刚体力学的凯恩方法推衍了系统的动力学方程，给出了考虑流固耦合和多体系统内部各物体间耦合的运动响应时域求解步骤。江召兵等[20]利用齐次矩阵方法对浮基多体系统的展开运动进行建模和分析。沈庆等[21]归纳总结了多刚体动力学和线性势流理论相结合的方法在海洋工程多体系统分析中的重要理论和实践意义。这些工作为海上重吊船动力响应特征分析提供了基本方法和分析思路。

现代海上重吊船的设计理念与传统陆上起重机和海洋单体浮式结构物的分析方法有所不同，其特点如下:①多学科优化技术。海上重吊船是综合空气动力学、水动力学、结构动力学、机械力学和自动控制等多学科技术的海洋工程装备，其承受的各种环境载荷、部件运动、结构振动响应和相应操作工况控制系统执行响应都高度耦合、相互影响，其设计是一个多学科优化过程。②刚柔耦合多体动力学计算方法。海上重吊船是一个复杂的刚柔耦合多体系统。动力响应分析需采用高效的非线性时程分析方法，对数学模型的建立和仿真工具的选择都要求很高。③关键区域结构强度分析。大型回转起重船自身结构构件类型复杂多样，且承受各类外载荷作用，作业时全船应力分布不明确，结构连接处可能会出现失效破坏，因此船体关键结构强度的高效准确计算成为保障船体安全需要解决的重要问题。本文主要分析了重吊船关键区域结构耦合响应特征，基于机械系统动力学自动分析(Automatic Dynamic Analysis of Mechanical Systems，ADAMS)软件构建反映上述特点的重吊船虚拟样机，将运动和动力耦合特征导入优化模块，给出典型多体多场系统关键区域结构主尺度方案，为复杂多体系统优化设计提供参考。

1 多体动力学仿真分析

ADAMS作为世界上使用最广泛的多体动力学软件，在航天、汽车等领域已得到成功应用。其多体动力学求解技术可更高效、准确地评估包括运动、结构、驱动和控制在内的各学科之间的复杂相互作用。

1.1 ADAMS多体动力学分析方法

1.1.1 ADAMS运动学方程

在ADAMS软件中，若整个机械系统刚性构件个数为n，运动副约束方程个数为m，则机械系统在广义坐标系下的运动学约束ΦK(q)方程组为:

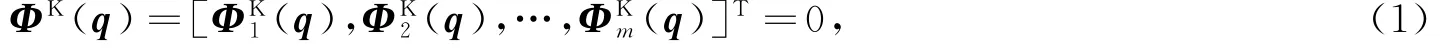
式中，K 为系统运动学约束，q为机械系统的广义坐标，T 为矩阵的转置。

若x表示广义坐标q的坐标数目，则当添加的驱动个数为(x-m)时，驱动约束为:

将式(1)和式(2)约束合并得到拥有x个非线性方程组:

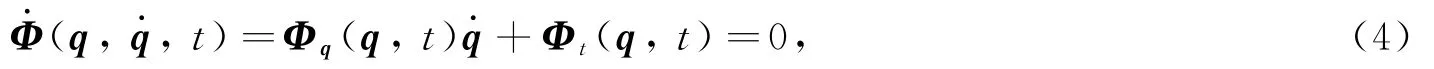
则系统的速度约束方程为:

1.1.2 ADAMS动力学方程

在ADAMS软件中，构件的质心直角坐标和表示构件位置、方向的欧拉角被当作广义坐标，记作q=[x，y，z，ψ，θ，φ]T，假设R=[x，y，z]T，γ=[ψ，θ，φ]T，那么q=[RT，γT]T。通过转换矩阵A gi进行质心参考坐标系和大地固定坐标系相互转换:

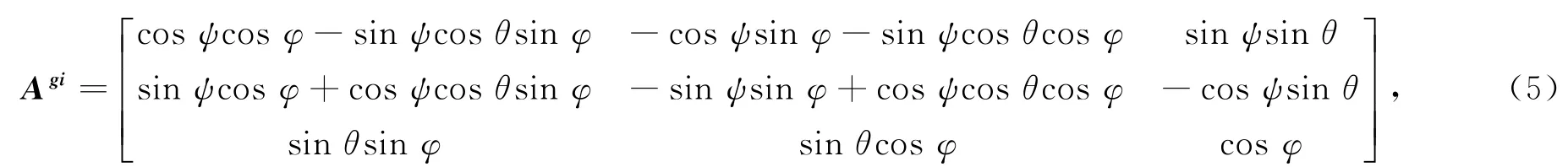
式中:x、y、z为构件坐标;ψ、θ、φ为构件角度坐标欧拉角。令换算矩阵为:

结合式(3)，通过带有Lagrange乘子的Ⅰ类方程式的能量形式[22]推导出表达式:

式中，E为系统广义坐标中具有的动能，q j为广义坐标，Q j为广义坐标中沿着q j方向上的作用力。

为了简化式(8)的表达形式，令:

将式(9)和式(10)代入式(8)得到:

系统的动能为:

把式(11)分解成沿着转动和移动方向的形式，可得:沿转动方向，

沿移动方向，

基于多体动力学理论知识，ADAMS系统的动力学方程组可表示如下:

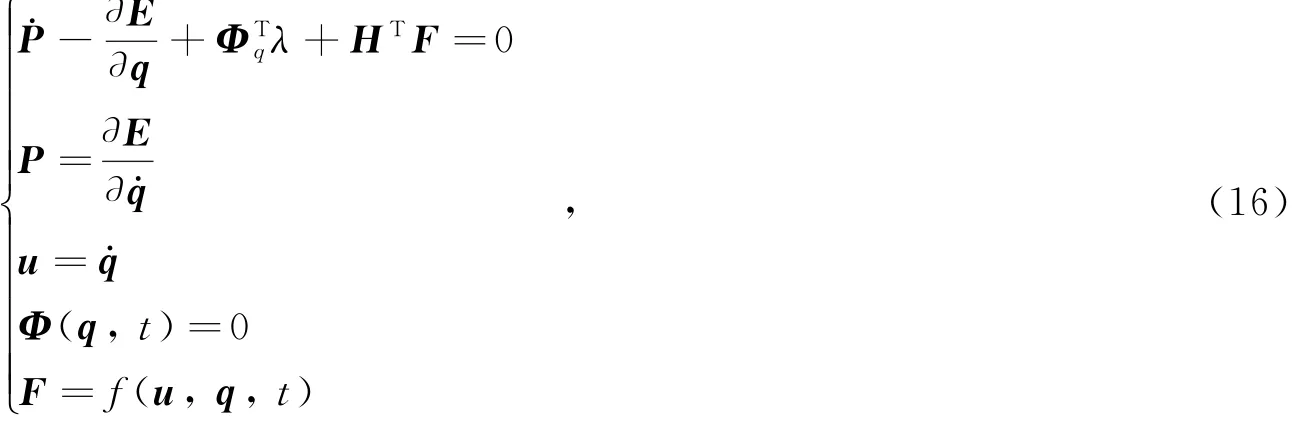
式中，E为系统广义坐标中具有的动能，λ为拉格朗日乘子，H为外部作用力到目标坐标系的转换矩阵，P为系统的广义动量，q为系统的广义坐标，u为系统广义坐标下的速度，Φ为q的运动学约束方程，F为外力矩阵，t为时间。

1.2 重吊船刚柔耦合虚拟样机

海上大型回转起重机在启动、回转、止动和其他工作状态突变时，机械系统将产生强烈的振动，从而诱发吊物系统产生复杂动力响应。ADAMS软件可将系统环境激励响应、结构构件、机械部件、控制系统集成，构建试验虚拟样机，准确反馈子系统之间的相互作用。

1.2.1 刚性体及柔性体建模

基于ADAMS多体分析平台，利用虚拟样机技术，结合多个软件完成全回转重吊船刚柔耦合模型的建立。利用ANSYS有限元分析软件中的WORKBENCH-Geometry完成重吊船三维模型的构建(图1)，将船体、转台及配重、导管架区段(吊物质量5 000 t)作为刚体导入ADAMS软件。

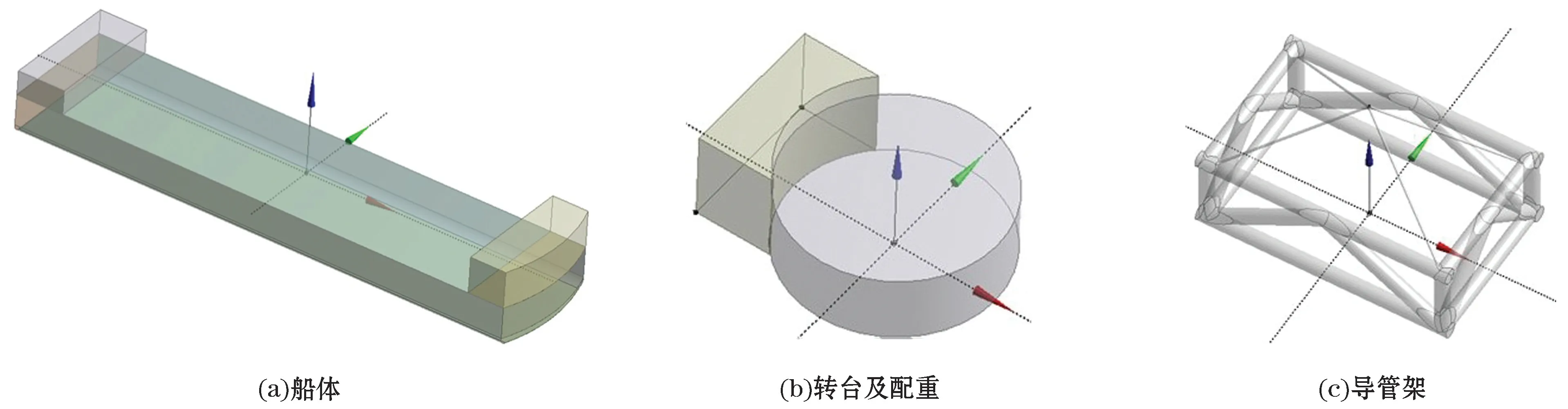
图1 刚体模型Fig.1 Rigid body modeling

利用ANSYS参数化设计语言ANSYS-APDL(ANSYS Parametric Design Language)完成支撑、臂架的建模(图2)，并将支撑和臂架作为柔性体导入ADAMS软件中。采用刚性区域法[23]建立刚性区域，完成刚、柔性体的连接。

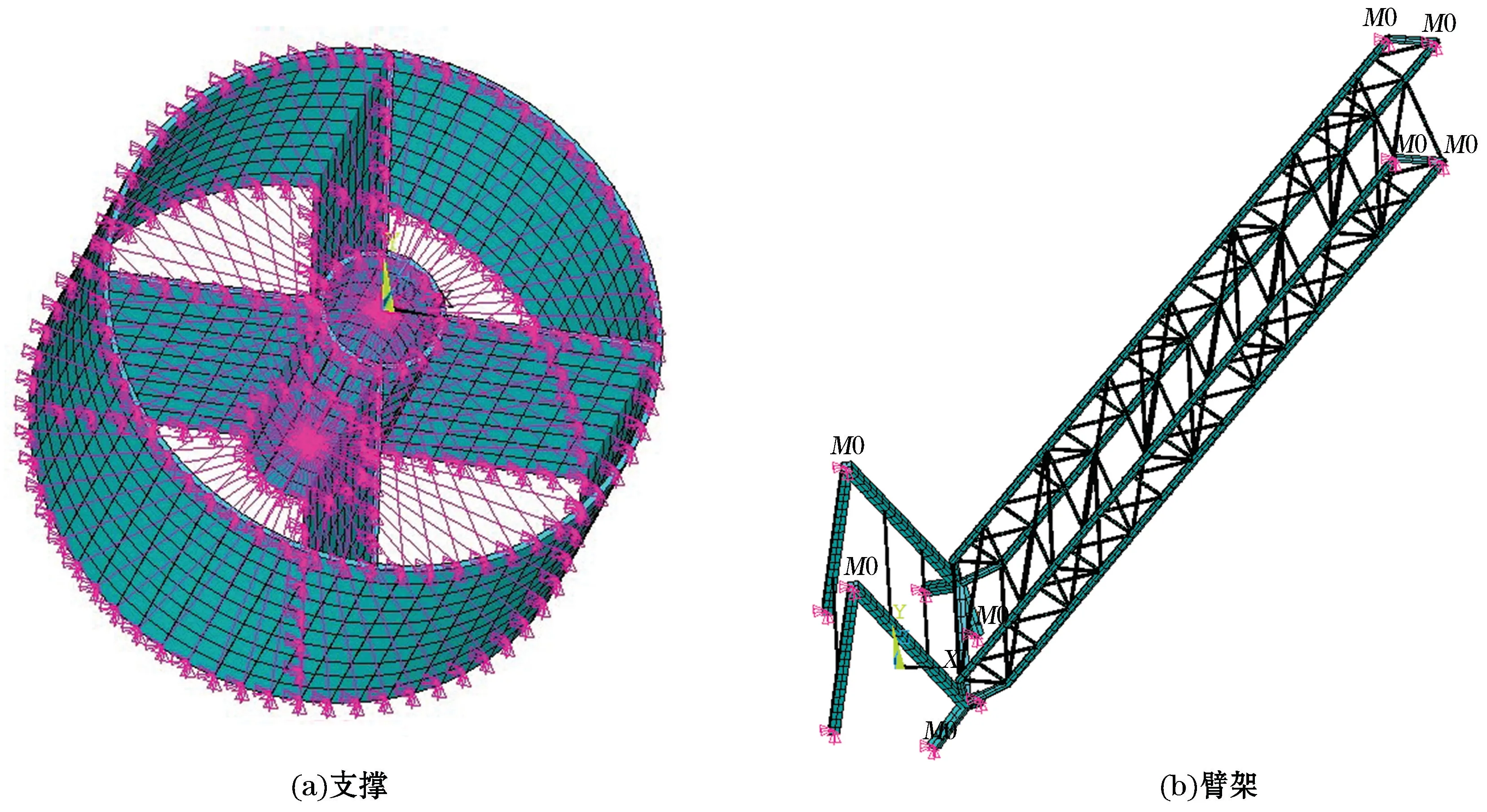
图2 柔性体模型Fig.2 Flexible body modeling

1.2.2 ADMAS起重船虚拟样机建立

将刚性体、柔性体构件导入ADAMS软件后，搭建起重机吊装绳索系统完成起重船虚拟样机的建立，虚拟样机由船体(刚体)、支撑(柔性体)、配重及转台(刚体)、导管架区段(刚体)、臂架(柔性体)、4个桁架(刚体)、3套用于控制臂架变幅的绳索(弹性体)及1套吊装绳索(弹性体)组成(图3)。其中绳索作为弹性体，支撑及臂架材料密度ρ=7 850 kg/m3，弹性模量E=2.1×1011Pa，通过固定副的施加实现系统内相互运动多体子结构的运动传递。

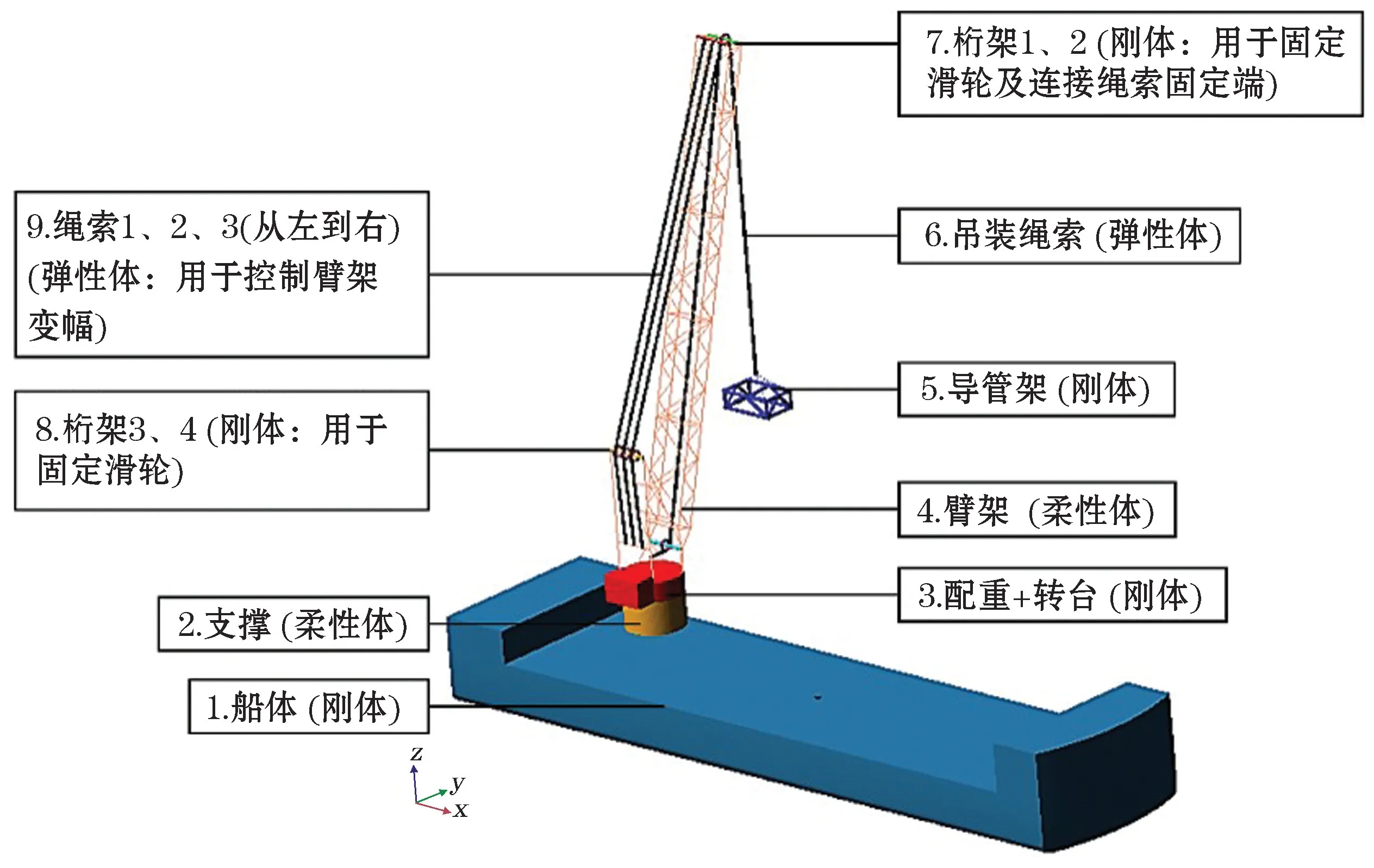
图3 重吊船虚拟样机Fig.3 A virtual prototype of the full swing heavy lifting vessel

1.3 船体运动传递下重吊船时域响应分析

重吊船、吊物之间运动和动力的传递与耦合是复杂的，通过ADAMS软件对建立完成的重吊船虚拟样机仿真模拟，能够比较准确地反映船体、起重机系统、吊物之间的空间关系以及运动学和动力学特性。对重吊船虚拟样机施加驱动，提取时程响应数据，可以客观地分析多体耦合运动对结构响应的影响。

1.3.1 船体运动响应

重吊船在有义波高2.5 m、谱峰周期6.5 s、风速10 m/s、流速1 m/s的海况下作业。利用AQWA 完成水动力计算，时域分析的时间步长取0.1 s，考虑低频载荷影响的不规则波分析，模拟时长3 h。在风、浪、流均为90°入射时计算船体横摇、垂荡运动响应，在风、浪、流均180°入射时计算船体纵摇运动响应，结果如图4所示。结果表明，起重船的最大横摇为0.50°、最大纵摇为0.13°、最大垂荡为12.19 m。

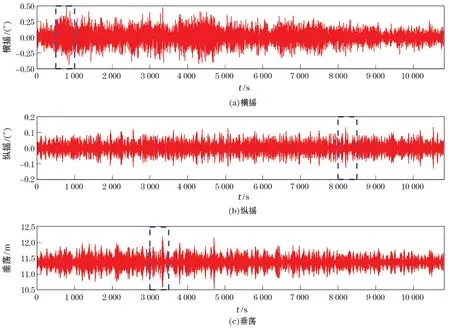
图4 船体横摇、纵摇和垂荡运动响应计算结果Fig.4 Calculation results of the responses of roll，pitch and heave motion of the hull

1.3.2 多体运动与动力耦合响应

船体在不同运动状态下，变幅绳索和吊装绳索的张力相对于船体静止时的绳索张力增幅见表1。由表1可知，对比船体静止时，变幅绳索1、2、3(图3)的张力增幅在船体横摇、垂荡耦合运动时最大，吊装绳索的张力增幅在船体纵摇、垂荡耦合运动时最大。结果表明，横摇、垂荡耦合运动对变幅绳索的影响较大，纵摇、垂荡耦合运动对吊装绳索的影响较大。

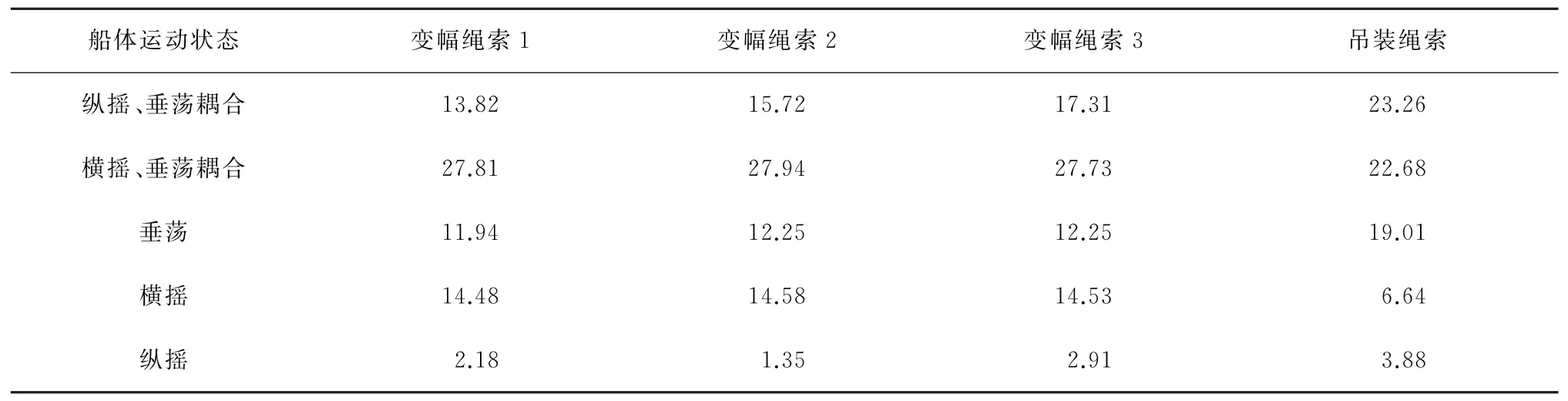
表1 相对船体静止绳索张力相对增幅Table 1 Increase of the rope tension relatively to the still hull %

图5为船体静止与横摇、垂荡耦合运动下变幅绳索的张力曲线。可见船体的横摇、垂荡耦合运动会使变幅绳索张力有较大的增幅。船体静止时绳索1张力的峰值为3.96×107N，船体横摇、垂荡耦合运动下绳索1张力的峰值为5.06×107N;对比船体静止情况，横摇、垂荡耦合运动导致的绳索1张力增幅为27.81%。船体静止时绳索2张力的峰值为3.95×107N，船体横摇、垂荡耦合运动下绳索2张力的峰值为5.06×107N;对比船体静止情况，横摇、垂荡耦合运动导致的绳索2张力增幅为27.94%。船体静止时绳索3张力的峰值为3.96×107N，船体横摇、垂荡耦合运动下绳索3张力的峰值为5.06×107N;对比船体静止情况，横摇、垂荡耦合运动导致的绳索3张力增幅为27.73%。

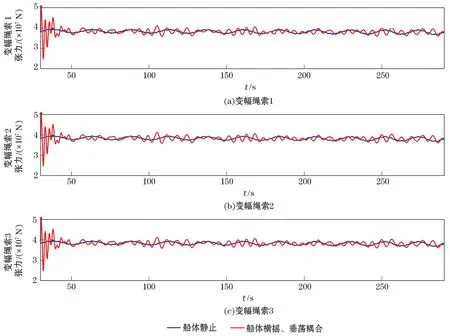
图5 船体静止与船体横摇、垂荡耦合运动情况下变幅绳索1、2、3张力结果对比Fig.5 Comparison of luffing rope tension under the cases of hull still and coupling motion of pitch and heave

由船体静止与纵摇、垂荡耦合运动情况下吊装绳索的张力曲线(图6)可见船体的纵摇、垂荡耦合运动会使吊装绳索张力有较大的增幅。船体静止时吊装绳索张力的峰值为4.92×107N，船体纵摇、垂荡耦合运动情况下吊装绳索张力的峰值为6.07×107N;对比船体静止情况，耦合运动使吊装绳索张力增幅23.26%。船体在不同运动状态下，支撑处应力相对于船体静止时的应力增幅见表2。由表2 可知，对比船体静止情况，支撑结构最大应力对应节点处的应力增幅在船体横摇、垂荡耦合运动时最大，其应力时程曲线对比如图7 所示。船体静止时支撑结构最大应力对应节点处应力变化的峰值为6.44×107Pa，船体横摇、垂荡耦合运动下支撑结构最大应力对应节点处应力变化的峰值为8.17×107Pa;对比船体静止情况，横摇、垂荡耦合运动导致的节点应力增幅为26.94%。

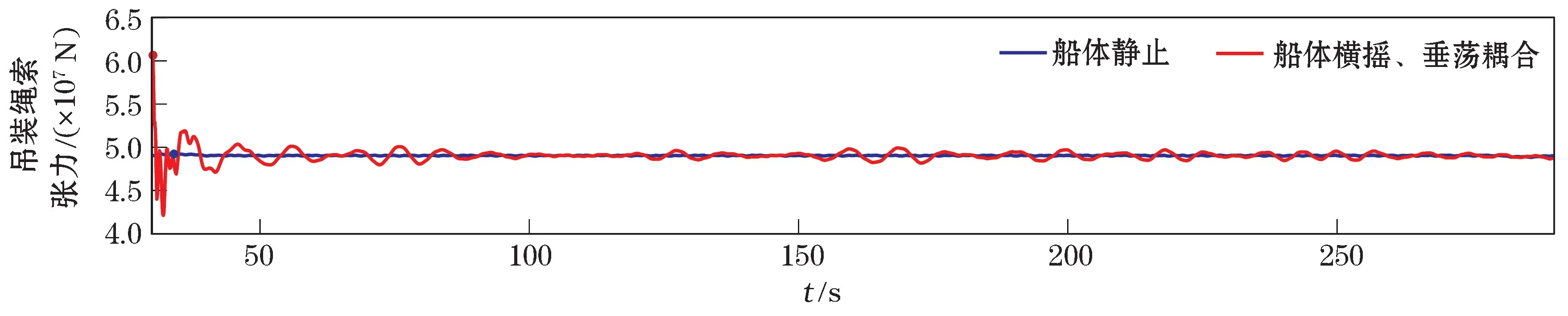
图6 船体静止与船体纵摇、垂荡耦合运动情况下吊装绳索张力结果对比Fig.6 Comparison of hoisting rope tension under the cases of hull still and coupling motion of hull roll and heave

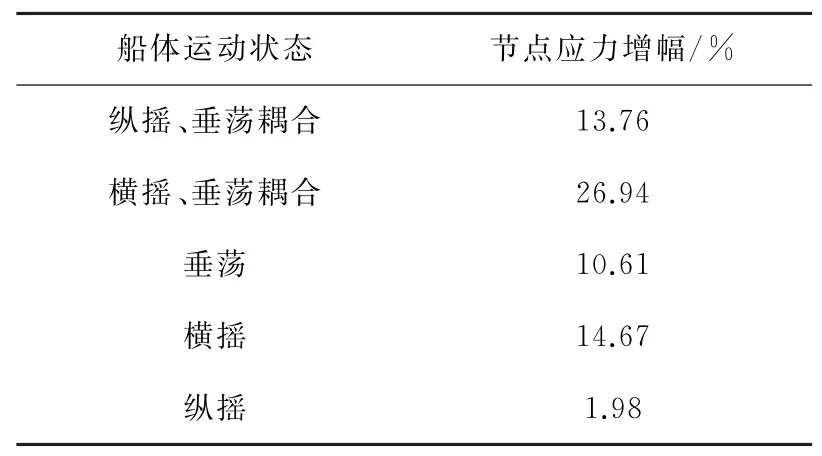
表2 相对船体静止节点应力增幅Table 2 Increase of the node stress relatively to the still hull

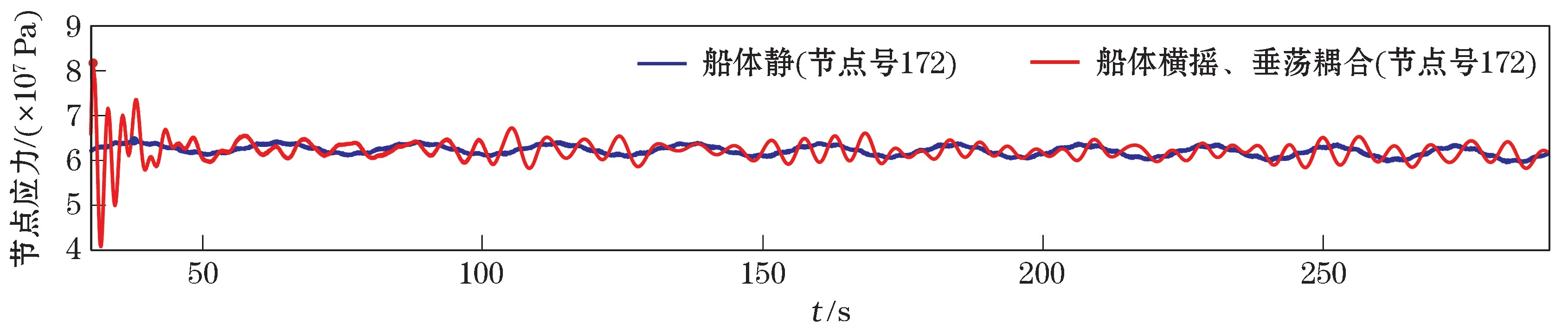
图7 船体静止与船体横摇、垂荡耦合运动情况下节点应力结果对比Fig.7 Comparison of node stress under the cases of hull still and coupling motion of hull roll and heave

2 关键区域结构优化设计

支撑结构是连接起重机和船体的关键区域，其可靠性直接决定了重吊船作业的安全性。通过上述耦合应力分布规律，依托WORKBENCH 优化模块给出多目标最优的支撑结构加强筋布置方案。

2.1 重吊船关键区域结构有限元模型

在WORKBENCH 模块中建立转台、配重和支撑结构的有限元模型。在起吊作业时，支撑的受力主要是由绳索系统和臂架产生的动力响应引起的。支撑的内壁、外壁及肘板的厚度与ADAMS软件中的支撑柔性体一致，初值设置为0.2 m，转台、配重与支撑的接触类型设置为绑定，有限元模型如图8所示。

图8 支撑结构有限元模型Fig.8 The finite element model of support structure

2.2 虚拟样机多体耦合响应导入

在ADAMS软件中，支撑结构作为柔性体，起重机的臂架及各绳索通过标记点1至标记点7将力传递到转台上(图9)，继而传递到支撑结构上。在ADAMS仿真中提取标记点1至标记点7上力的时程数据，当t=37.74 s时，支撑结构节点应力最大，将此时7处标记点上的力施加到有限元模型上，如图10所示，全约束支撑结构底部的边界，网格大小同ADAMS软件中模型网格划分大小一致，即1 m×1 m，进而完成静力分析。当t=37.74 s时，7处标记点上的力如表3所示。

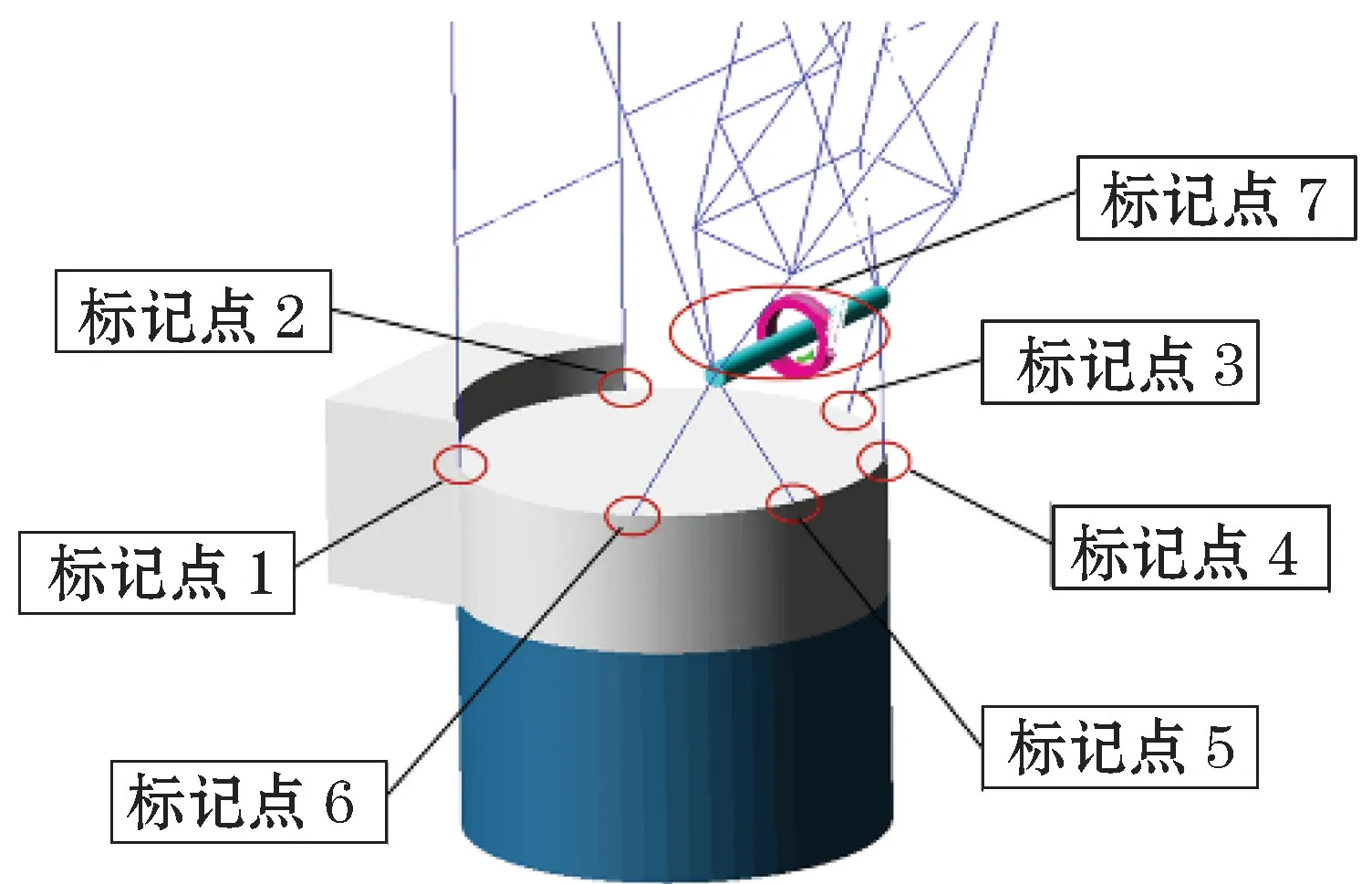
图9 力的传递标记点Fig.9 Force transfer marking points

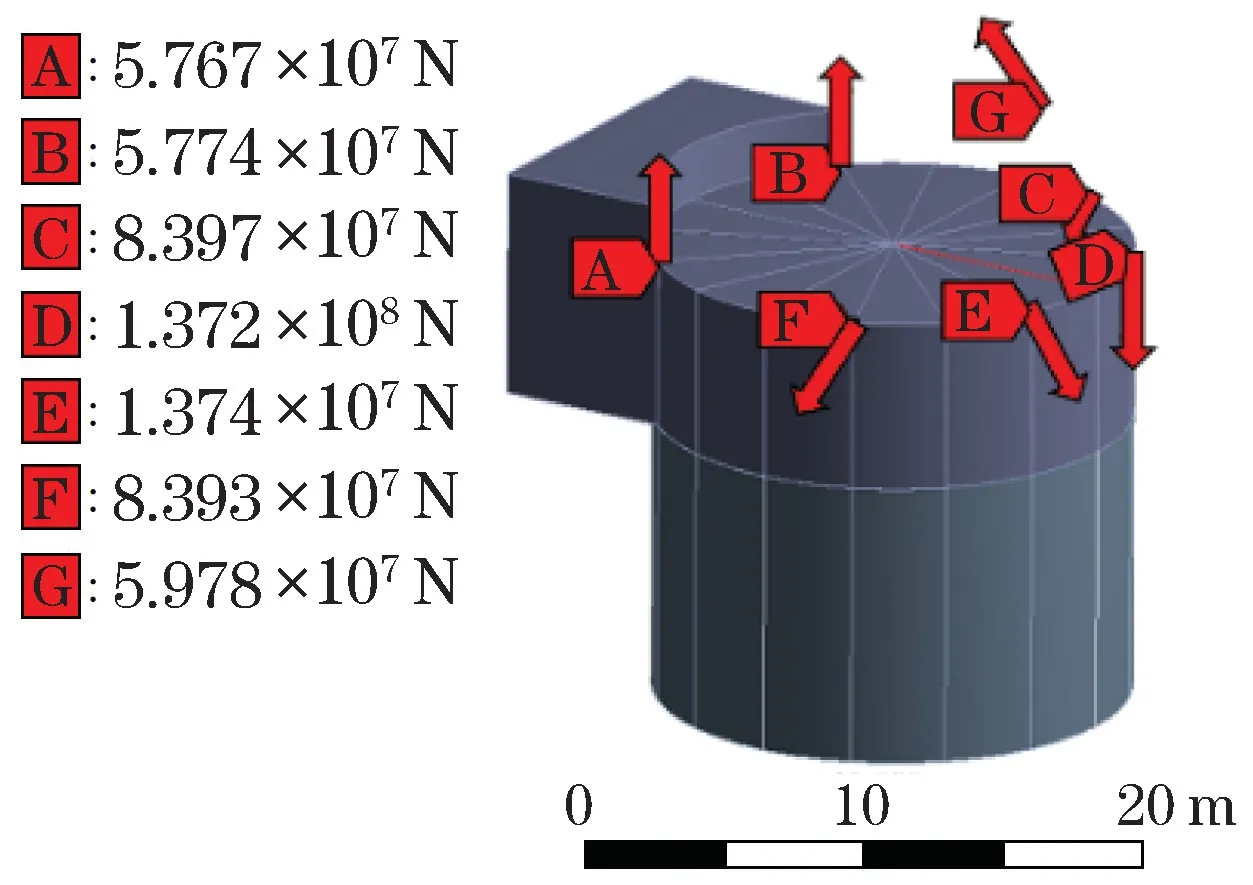
图10 有限元模型施加的力Fig.10 The force exerted by the finite element model

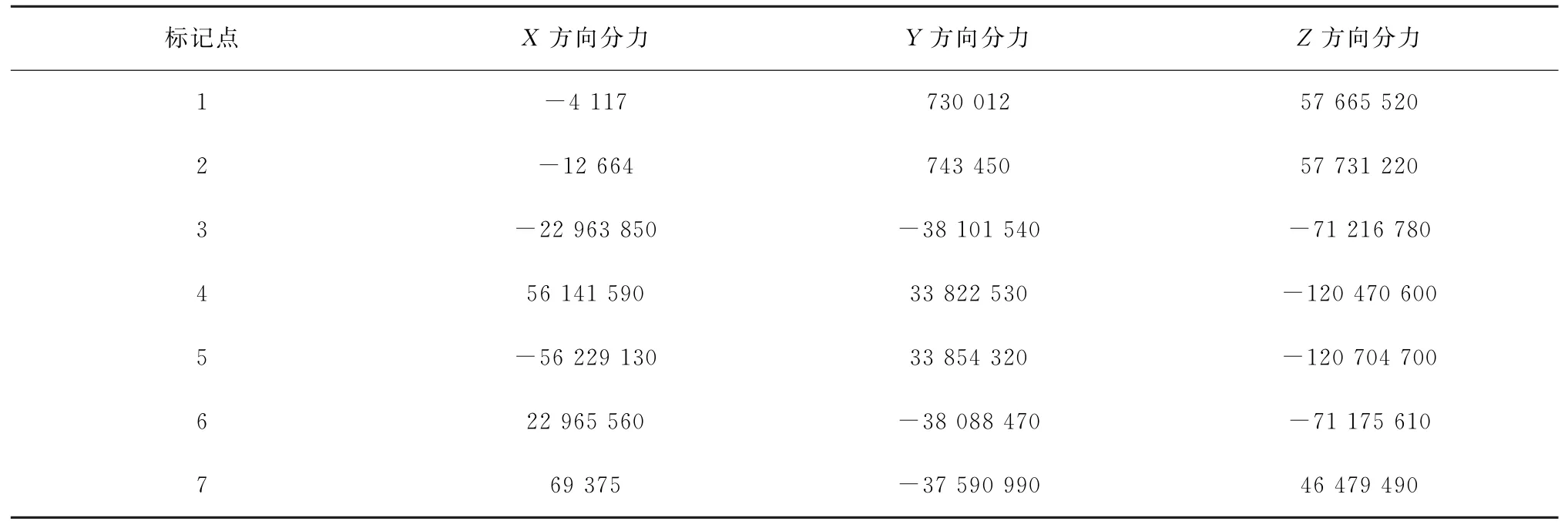
表3 当t=37.74 s时,7处标记点上的力Table 3 The force at seven mark points when t=37.74 s N

2.3 优化结果与讨论

2.3.1 关键区域结构设计

在分析重吊船动力响应规律和支撑结构的应力分布特点时，支撑的内壁、外壁及肘板厚度初值设定为0.2 m。起重机回转作业时，启动和制动加速度绝对值为0.05(°)/s2，各耗时10 s，匀速回转速度为0.5(°)/s，耗时170 s，完成逆时针回转90°，通过虚拟仿真模拟得到支撑结构应力分布的时程变化如图11所示。

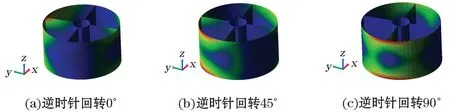
图11 起重机逆时针回转时支撑结构应力分布的时程变化Fig.11 Time-course variation of the stress distribution of the support structure when the crane rotates counterclockwise

根据支撑结构应力分布特点设置加强筋，加强筋类型设定为T 型材，WORKBENCH 模块中T 型材结构无圆角半径。支撑结构的钢材选用Q345钢，即屈服极限为345 MPa。T 型材尺寸及支撑板厚度初步设计方案如表4所示。

表4 T型材尺寸及支撑板厚度Table 4 Size of the T-section bar and thickness of the support plate m

2.3.2 关键区域结构优化方案

以支撑结构应力最大值最小及支撑钢材重量最小为优化目标完成优化计算。设计变量取值如表5所示，由于内壁的应力值很小，对优化结果无影响，设定其壁厚为常数0.02 m。T 型材采用窄翼缘T 型钢，其腹板高H大于翼板宽B，该约束与支撑结构197 MPa的许用应力C构成约束变量，可表示为:

表5 设计变量初始值及取值范围Table 5 Initial values and value ranges of the designed variables m

此外，用Min max(EquivalentStress)表示等效应力最大值最小，Min Weight表示支撑结构重量最小，两者与式(17)组成了结构优化的数学模型。

优化模块Design Exploration基于多目标遗传算法(Multi-objectives Genetic Algorithms，MOGA)[24]，最初生成了100个样本，最大迭代次数设置为5，每次迭代生成50个样本。设定对第一次计算错误的设计点进行3次重复计算，每次计算间隔1 min，以避免因计算机内存问题导致优化失败。优化完成后得到结构设计方案及Pareto前沿，如图12所示;结合客观熵权TOPSIS决策方法[25]得到的最终优化的支撑结构方案，如表6所示。

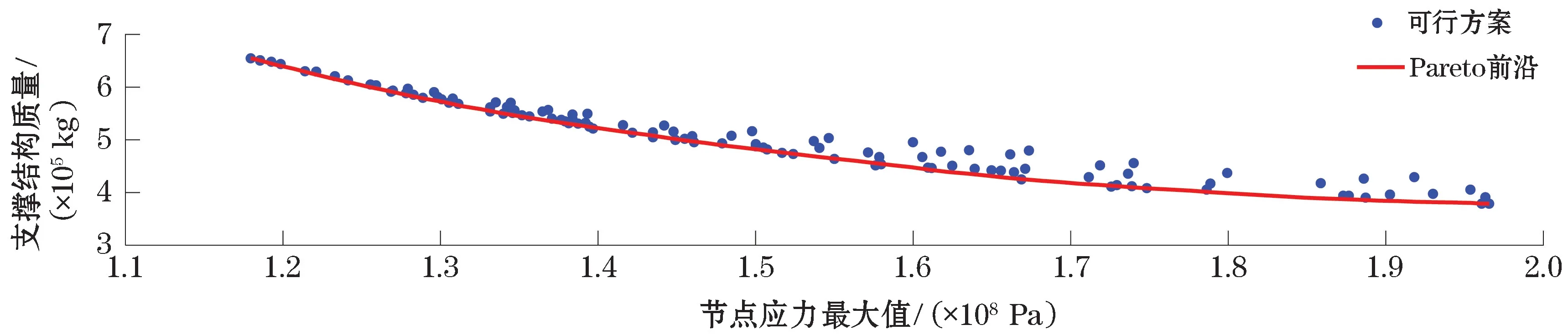
图12 可行方案及Pareto前沿Fig.12 The feasible schemes obtained after optimization and the Pareto frontier

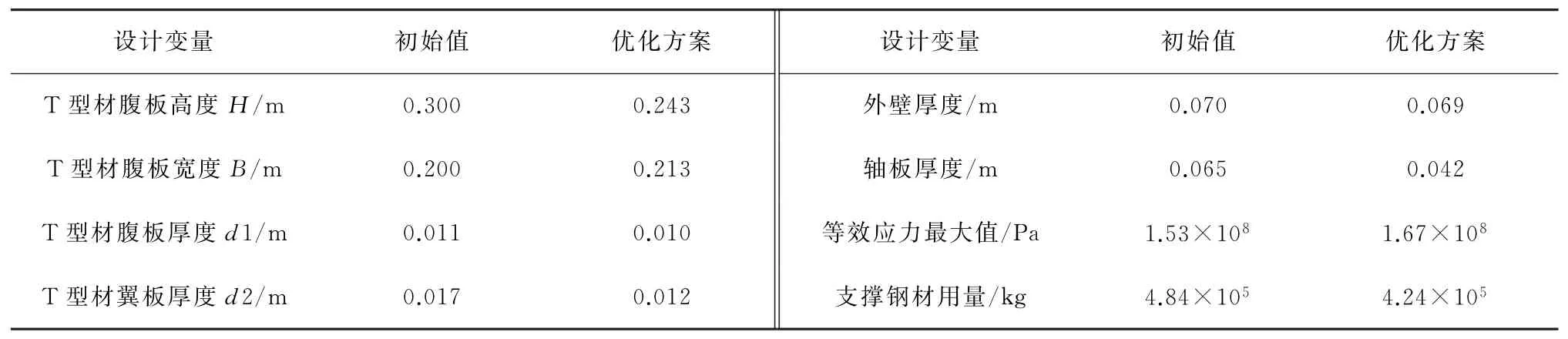
表6 支撑结构优化方案Table 6 Optimized scheme of the support structure

初始方案中，等效应力最大值为1.53×108Pa，支撑钢材用量为4.84×105kg;优化方案中，等效应力最大值为1.67×108Pa，支撑钢材用量为4.24×105kg。对比初始方案，优化方案使支撑结构质量减轻了12.30%。

3 结 语

关键结构区域失效是制约全回转重吊船安全作业的重要因素。本文将虚拟样机技术与有限元分析方法结合，构建重吊船刚柔耦合一体化分析模型，以典型作业海况引起的船体运动驱动，探究多体系统运动和动力耦合特征，采用多目标优化与多准则决策方法给出了关键区域设计分析流程。具体工作总结如下:

1)海上全回转重吊船时域响应驱动的刚柔耦合虚拟样机构建。利用SOLIDWORKS 或WORKBENCH 建立船体刚性模块，利用ANSYS-APDL建立支撑结构及主要传力构件柔性模块，通过ADAMS实现全回转重吊船的刚柔耦合虚拟样机组建。

2)海上全回转重吊船典型海况多体动力学仿真求解。通过AQWA 计算船体在压载方案下的运动响应驱动全回转重吊船虚拟样机，完成回转作业全时域动力耦合分析。研究表明船体横摇及垂荡对动力响应影响较大。在横摇、垂荡耦合运动时对变幅绳索的张力和支撑结构的应力影响较大，对比船体静止情况，该耦合运动导致的节点应力增幅为26.94%;在纵摇、垂荡耦合运动时对吊装绳索的张力影响较大。对比船体静止情况，该耦合运动导致的吊装绳索张力增幅为23.26%。

3)关键结构区域多目标优化与多准则决策。将多体耦合响应分析结果导入有限元软件完成关键区域支撑结构强度分析，根据应力分布特点及支撑型材设置，运用多目标优化算法结合客观熵权TOPSIS决策方法给出了支撑结构优化方案。对比初始方案，优化方案使支撑结构质量减轻12.30%。

本文验证了虚拟样机处理运动与动力耦合分析的可行性，采用多目标优化与多准则决策结合的方法对船舶起重机关键区域优化设计提供了新思路。文中仅取横摇、纵摇、垂荡数据中幅值相对大的区段驱动虚拟样机，没有考虑耦合数据相位对动力响应的影响，同时环境荷载工况也仅作了风、浪、流同向假设，起重机臂架的变幅角度对多体动力响应的干扰也未做讨论，后续需要进一步发展相应的精细耦合模型。