黄河下游引黄灌区输沙渠道优化设计
2022-04-07费祥俊
费祥俊
(清华大学 水利水电工程系,北京 100084)
黄河下游的河南、山东两省建有规模很大的引黄灌区,其中万亩(15 亩为1 hm2)以上灌区近100 处,年均引水量约100 亿m3,引沙量达1.2 亿t。 如何输送这些泥沙,避免渠道堵塞,是灌区工程建设应考虑的重要问题。 沿黄两岸分布有适宜沉沙的天然低洼自流区,利用渠首沉沙池集中沉沙是早期引黄泥沙处理的主要方式。
由于早期渠道设计缺乏经验及运用管理不当,因此泥沙淤积严重。 山东省地面平缓,坡降为1/7 000 ~1/8 000,渠道输沙能力受限制,选择修建沉沙池以减轻渠道淤积。 然而引黄泥沙大部分淤积在沉沙池和渠系内,送入田间的泥沙很少。 如典型的位山灌区,两条各15 km 长的东西输沙渠,形成了宽100 m 左右、高6 m的堆沙带,占地400 多hm2。 河南省黄河比降较大,地形有利于输沙,但在局部地区也有严重淤积,如人民胜利渠灌区东三干渠两侧,渠道清淤堆沙量也非常可观,同样有土地沙化现象[1-2]。 采用清淤方法,将清出的泥沙集中堆积在灌区的上游地段,不仅会带来沉重的经济负担,还将压占堆沙土地、引起土地沙化、造成风沙灾害,严重影响周围的生态环境。
如果利用黄河下游输沙平衡关系优化渠道设计断面,可大幅度提高渠道输沙能力,实现输沙入田,既有利于减少下游河道淤积,又能为引黄灌溉带来巨大效益。 引黄输沙渠道的设计,一要有可靠的黄河下游河道输沙能力或不淤流速公式,二要采用最优或较优的渠道断面形态。 但现有的渠道输沙能力公式大多为观察数据点绘得来的经验公式,这些观察点据多数不符合平衡输沙条件。 由于各人引用资料及处理方法不同,因此出现很多互不通用的输沙能力或不淤流速经验公式,至于渠道断面形态优化问题更未考虑。 因此,笔者利用研究得到的相关公式,计算最优断面参数,从而优化渠道设计。
1 黄河下游河道输沙能力及不淤流速关系式的建立
根据最近研究,黄河下游河道输沙平衡关系为[3]
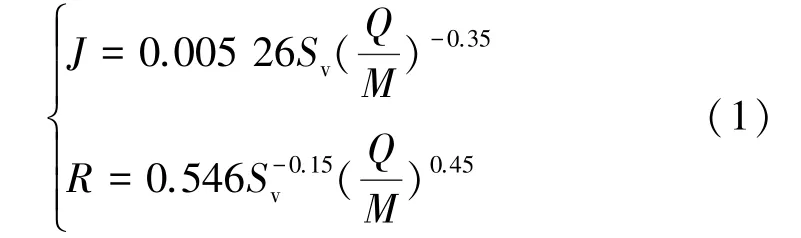
式中:J为比降;R为水力半径;Sv为体积比含沙量,代表河道的输沙能力;Q为流量;M为河道断面参数,为湿周P与水力半径R之比,对宽浅型河道为宽深比。
将流量公式Q=MR2U代入式(1)中的水力半径公式,可得黄河下游输沙能力和不淤流速公式:

式中:U为不淤流速;h为水深。
对于不淤流速, 常用的还有肯尼迪公式U=0.548h0.64,拉塞公式U=0.645R0.5等[4]。
2 输沙渠道的断面参数及优化
由式(2)可知,在流量和水深一定时,输沙能力Sv与M和R均为负相关。 为了求出最小的M,可以写出渠道湿周P和断面面积A的计算公式[5]:
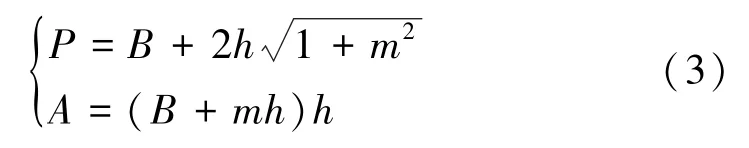
式中:B为河宽;m为边坡系数。
式(3)中两式消去B,由于R=A/P及M=P2/A,因此

为使式(4)有解,最小断面参数为
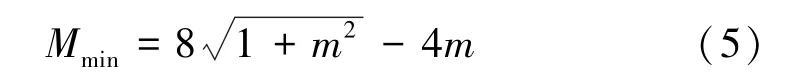
此时R=h/2 同样取得最小值,所以此断面参数下的输沙能力是最强的。 考虑工程经济及施工条件等因素,梯形断面边坡系数可随设计流量增大而增大,建议的m值见表1。

表1 不同流量下梯形断面边坡系数
在实际应用中,由于流量变化、地形条件及其他各种原因,因此不可能也没有必要严格采用Mmin。 为了在设计流量下留有余地,断面参数M值可略大于Mmin。 为此,参考式(5),不同设计流量下M的适宜取值见表2[6-7]。

表2 不同流量下梯形断面参数M 适宜值
当前,许多引黄灌区渠道边坡系数不满足最优设计,导致占地面积大,且输沙效果不理想。 利用式(5)、表1 和表2,可以对其优化改进。 图1 展示了山东簸箕李灌区总干渠优化前后的对比,在相同流量及纵坡下,优化设计渠道断面面积不到原设计的一半,而输沙能力却增加到原来的十几倍,这说明此优化方案是有效的。 具体计算将在下文展开。

图1 山东簸箕李灌区总干渠断面原设计和新设计对比
3 渠道断面优化计算方法及讨论
3.1 设计流量下的渠道断面尺寸计算
引黄灌溉渠道的纵坡受制于地形条件,流量则取决于灌溉面积及植物需水情况,故J和Q是已知量,设计主要任务是确定断面尺寸及核算渠道的输沙能力。
以山东滨州簸箕李灌区总干渠为例,引水设计流量Q=65 m3/s,渠道纵坡J=1/5 000,采用边坡系数m=2的梯形断面并加衬砌。 根据表2,取M=11.3。 由式(1)可计算得到Sv=0.070,R=1.79 m,再计算出湿周P=MR=20.23 m。 对式(3)中两式联解,消去B,则有:
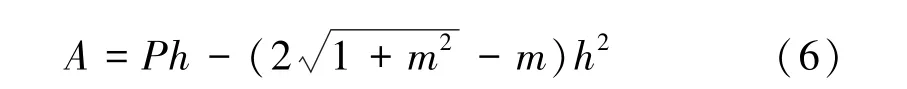
代入相关数据,结合一般h/R=1.3 ~1.7,即可解出h=2.64 m,根据式(3)得B=8.42 m。 渠道原设计和新设计的参数对比见表3。 其中,原设计的U是实际流速,改进以后的U是通过式(2)计算的不淤流速,通过肯尼迪公式和拉塞公式计算的结果分别为1.02、0.86 m/s。 由表3 可知,相同设计流量及纵坡下,新设计输沙渠道的过流面积不到原设计渠道的一半,表明其占地面积及工程量远小于原设计值。 原设计的输沙能力只有新设计的7%,所以必然要淤积。

表3 簸箕李灌区总干渠原设计与新设计比较
再如河南人民胜利新东一干渠[2],是20 世纪50年代初期修建的人民胜利渠的一部分。 对比原设计和新设计,见表4。 用肯尼迪公式和拉塞公式计算出的不淤流速分别为0.91、0.74 m/s,虽然小于原设计流速,但这里原渠道的最大输沙量只有最优值的17%,来沙过多同样会导致淤积严重。

表4 人民胜利新东一干渠原设计与新设计比较
由表3 和表4 可知,原设计断面参数都偏离优化值,前者偏大,后者偏小,都会造成淤积。 需要注意的是,根据曼宁公式计算,新设计渠道的曼宁粗糙度都在0.02 左右。 工程上为了达到这样较小的粗糙度,可以用混凝土衬砌渠道。 这样不仅能提高输水输沙效率,还能防冲固坡,保障生产安全,在包括胜利干渠在内的全国各地都得到了广泛利用[8]。 当然,这样计算出的Sv只是理论值,实际输沙效果还要取决于实际工程。
3.2 流量和含沙量对渠道水深变化的影响
渠道运用流量一般大于设计流量,设计确定的渠道底宽不变,水深将随流量加大有所增加。 仍以簸箕李灌区为例,水深和其他渠道参数与流量的关系见表5。

表5 簸箕李灌区总干渠加大流量后的参数
增大流量以后,输沙能力有所增加,但同时也会造成水深加大。 当流量增大到设计值的两倍时,超高达到了1.27 m,已经过大。 这说明运用流量也应当有所限制。
另外,式(1)中的Sv是平衡条件下的渠道输沙潜力,而实际来自河道的Sv相对很小。 通过类似的计算发现,来沙减少同样会造成超高增加,所以输沙渠道优化设计应考虑来水来沙可能变化范围,确定适当的断面水深超高值。 正常而言,优化设计的渠道输沙能力有富余,淤积出现的概率很低。 但运用流量持续小于设计流量,渠道也会有累积性淤积。 渠道运用中,应尽可能避免长时段低于设计流量运用。
4 结语和建议
开展引黄灌溉渠道优化设计,提升渠道输沙能力,输沙入田,不仅有利于发展黄河下游沿黄两省农业生产,还会改善黄河下游河道条件和灌区土壤环境,有助于黄河流域的高质量发展,值得高度重视。
研究发现,引黄渠首及渠系泥沙淤积严重的原因,除运用不当外,主要是早期渠道设计不合理,没有根据可靠的河段输沙能力或不淤流速公式来核算渠道的输沙能力,更没有根据水力最优断面参数来确定渠道断面尺寸[9]。 淤积问题出现后,有关单位进行了大量试验研究,包括采用U 形断面、增加衬砌及提高纵坡等,但缺乏基础性研究,基本上仍用20 世纪50 年代以来的各种输沙能力经验公式,或新增一些经验公式,以致渠首及渠系泥沙淤积改善不多,清淤泥沙不断积累,影响周边地区的环境质量。
最优断面参数可为黄河下游引黄渠道设计或改造提供新的理论支持。 为此,建议应用新的科技成果,逐步改造引黄渠系。 输沙渠道优化设计的原理与方法,同样适用于黄河下游的放淤渠道,从而实现高含沙水流远距离输送。 对于放淤渠道,还可利用滩区横比降大的优势,通过尺度相对较小的渠道输沙淤滩或两岸洼地。
需要进一步研究的问题有两个:一是渠道断面优化,水力半径减小,可能导致输送距离缩短,影响输沙入田;二是渠道断面优化,更有利于高含沙水流输送,但仍需要讨论如何控制渠道水流的含沙量,充分利用其输沙能力。
