利用粒子群算法改进电离层TEC预报模型

杨淑芬，曾 聪，唐钰涵

(中交第二公路勘察设计研究院有限公司，武汉 430056)

电离层对穿越其中的无线信号造成折射和延迟，对基于卫星的导航定位、位置服务、遥感、遥测等造成严重影响。美国方面取消SA政策后，电离层延迟和多路径效应被认为是影响GNSS定位精度的最大误差源[1]。因此，研究电离层总电子含量(total electric content, TEC)的变化规律并对其进行预报，建立精确可靠的电离层延迟改正模型对实际应用具有十分重要的意义[2]，电离层TEC预报已经成为电离层研究中的热点。文献[3]利用时间序列进行电离层TEC预报，预报的结果误差在3 TECu以内。文献[4]提出经验正交函数(empirical orthogonal function, EOF)与LSTM(long short-term memory, LSTM)神经网络相结合的预报方法，实现了区域格网电离层预报并提高了预报精度。文献[5]等通过最小二乘配置的方法进行长期预报和短期预报，预报精度为1～7 TECu。文献[6]建立集合经验模态分解(ensemble empirical mode decomposition, EEMD)与Holt-Winters组合的预报模型，在地磁平静期模型的相对精度最优可达91.71%，地磁活跃期最优可达86.83%。文献[7]提出小波分解和自回归移动平均(autoregressive moving average model, ARMA)相结合的短期电离层预报方法，预报精度较单一ARMA模型有显著提高。文献[8]重点分析了BP神经网络和ARMA两种模型在中纬度地区的预报效果，结果表明不同季节、不同电离层活跃情况下两种模型的预报性能各有优势。然而，上述预报模型大多存在参数选取困难、自适应性差、不同参数设置导致预报效果不稳定、偏差较大等一系列问题，如何建立自动化程度高、效果稳定的预报模型亟需进一步研究。

论文基于IGS中心提供的电离层产品，选取深度学习方法中最适合时间序列预报的长短期记忆神经网络利用粒子群算法(particle swarm optimization, PSO)自适应确定最优解的特性改进优化确定参数，得到最优神经网络模型，分别对低、中、高不同纬度的电离层TEC序列进行预报分析，以建立一种简洁高效、准确度高的PSO-LSTM神经网络模型。

1 模型原理

1.1 粒子群算法

Kennedy和Eberhart依据鸟群觅食行为启发于1995年首次提出粒子群算法。算法首先通过随机生成的方式在给定的解空间内生成粒子的初始位置以及初始速度，再根据需求解的问题确定适应度函数并计算出初始的适应度值，并得到个体局部最优解及全局最优解，最后通过粒子速度和位置的更新公式不断进行迭代得到解空间范围内的最优解。粒子速度和位置的更新公式如下：

(1)

(2)

1.2 LSTM神经网络

神经网络模型对复杂的非线性关系进行拟合具有速度快、精度高的优势，而电离层TEC时间序列数据因受到多种因素的影响呈现出非线性的特征，因此利用神经网络模型可以提高电离层TEC预报的精确度。LSTM神经网络[9]最早由Hochreiter和Schmidhuber在1997年提出，其已被证明在时间序列预报中能更好模拟数据的长期依赖性，记忆数据间的长期关系。相比于循环神经网络(recurrent neural network, RNN)，LSTM神经网络可以在更长的序列中取得较好的效果，能够对有价值的信息进行长期记忆。LSTM神经网络的神经元由遗忘门、输入门、更新门和输出门4个门限组成，它们的算式为：

ft=σ(Wf[ht-1,xt]+bf),

(3)

it=σ(Wi[ht-1,xt]+bi),

(4)

Ut=tanh(WU[ht-1,xt]+bU),

(5)

Ot=σ(WO[ht-1,xt]+bO).

(6)

式中:ft,it,Ut和Ot分别为4个门限；前一时刻输入值为ht-1、当前时刻输出值为ht、当前时刻变量输入值为xt；W为权重矩阵，b表示偏置项；σ和tanh分别为sigmoid和双曲正切激活函数。遗忘门判断是否读取ht-1，输入门判断xt是否用于更新上一时刻的神经元状态Ct，更新门判断Ct-1是否更新为Ct，输出门用于确定当前时刻的隐藏层输出值，与神经元状态值共同确定最终的预报结果。

1.3 PSO-LSTM神经网络模型

与其它神经网络相似，LSTM神经网络模型的训练参数如隐含层神经元个数和初始学习率难以确定，参数的选择对模型的精度和稳定性有较大程度的影响。为降低这种影响，利用粒子群算法对最优初始学习率进行参数寻优，提高LSTM神经网络模型的精度和稳定性，具体流程如下：

1)初始化粒子群参数，包括种群数量、最大迭代次数、学习因子、惯性因子、速度范围以及位置范围。

2)随机生成一组初始学习率，将LSTM神经网络模型预报结果的均方根误差作为适应度函数进行第一次迭代得到个体局部最优解和全局最优解，将其作为历史最佳位置。

3)利用粒子速度和位置的更新公式对种群的速度以及位置进行更新，并计算对应的适应度值。

4)当适应度值达到设置的精度要求时或模型达到设置的最大迭代次数时停止迭代并输出此时的全局最优解，将其作为最终的初始学习率输入到LSTM神经网络模型中进行模型训练得到TEC预报值，进行相应的精度分析。

2 实验分析及精度评定

2.1 实验分析

论文选取IGS中心提供的电离层产品进行实验，根据太阳活动选取2020年6月和12月的电离层TEC数据进行预报分析，对应年积日分别为152～181、335～364，两个时段的太阳活动指数(F10.7)如图1所示，从图中可以看出6月F10.7指数均在75以下，太阳活动平静，12月太阳活动明显剧烈，F10.7指数均在80以上。对低纬度(10°N 100°E)、中纬度(40°N 100°E)和高纬度(70°N 100°E)的TEC进行建模预报，利用数据前25 d作为样本序列，分别采用PSO-LSTM模型和ARMA模型、Holt-Winters模型、单一LSTM模型预报后5 d的TEC值。实验模型设置粒子群惯性因子ω为0.8、学习因子c1、c2均设置为0.5、最大迭代次数为50。LSTM神经网络模型的输入层数和输出层数设置为1层、隐含层神经元个数设置为200。将需要训练的TEC序列输入到神经网络中经粒子群算法对初始学习率进行寻优得到最优初始学习率，提高LSTM神经网络的预报精度。将模型的预报值与IGS中心提供的TEC实际值进行对比分析，通过均方根误差(RMSE)、相关系数(R)、平均残差(Δ)和平均相对精度(P)4个指标来评定精度，算式如下：

图1 2020年6月和12月F10.7指数

(7)

(8)

(9)

(10)

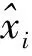
PSO-LSTM模型在两个时段的预报结果如图2和图3所示，从中可以看出电离层TEC数值在低纬度地区昼夜变化较大且其变化趋势较为规律，而在中、高纬度地区内变化较为复杂，规律性不明显。由于不同经纬度地区接受太阳辐射不同，在同一经度不同纬度上电离层电子含量之间的差值最大可达40 TECu，正常情形下，电离层TEC在不同纬度有着不同的变化规律，并会随着纬度变低而逐渐增大，这种现象增加了模型精确预报电离层TEC的难度。

图2 年积日177～181不同模型预报效果对比

通过图2和图3可以看出,PSO-LSTM模型在不同时段均表现良好，模型预报的结果与IGS中心发布的TEC值具有一致性，初步证明PSO-LSTM模型在预报电离层TEC上具有可靠性。同时，PSO-LSTM模型在低纬度地区预报精度较好，预报值与IGS中心提供的TEC值吻合程度最高。但是随着纬度的上升，诸如像磁暴和太阳活动等因素会较大程度影响电离层TEC变化，使得中、高纬度地区的电离层TEC预报精确度降低，并且随着预报天数的增加，预报精度也呈现逐步下降趋势。

图3 年积日360～364不同模型预报效果对比

电离层TEC变化与太阳活动密切相关，太阳活动剧烈时电离层受太阳辐射强度大，大气中性分子发生电离的能量增多使电离层电子含量多；太阳活动平静时地球接受太阳的辐射强度小，电离空气分子的能量减少，使得电离层电子含量低。通常夏季7月份和冬季11月份的电离层电子含量相差至少3倍以上，但有时也会出现相反的情形，即冬季的电子含量比夏季的电子含量大，称这种现象为“季节异常”[10]。通过图2和图3可以看出，ARMA模型在预报时的精度相比较其他3个模型而言精度较低，而对于Holt-Winters模型、LSTM模型和PSO-LSTM模型预报精度的高低通过图形无法直接判断，需进一步计算确定。

2.2 精度评定

通过参考IGS提供的电离层TEC产品，对不同模型预报得到的电离层TEC预报值进行精度评定，分别计算得出不同模型在低、中、高纬度地区预报结果的均方根误差、平均相对精度、相关系数和平均残差如表1和表2所示。

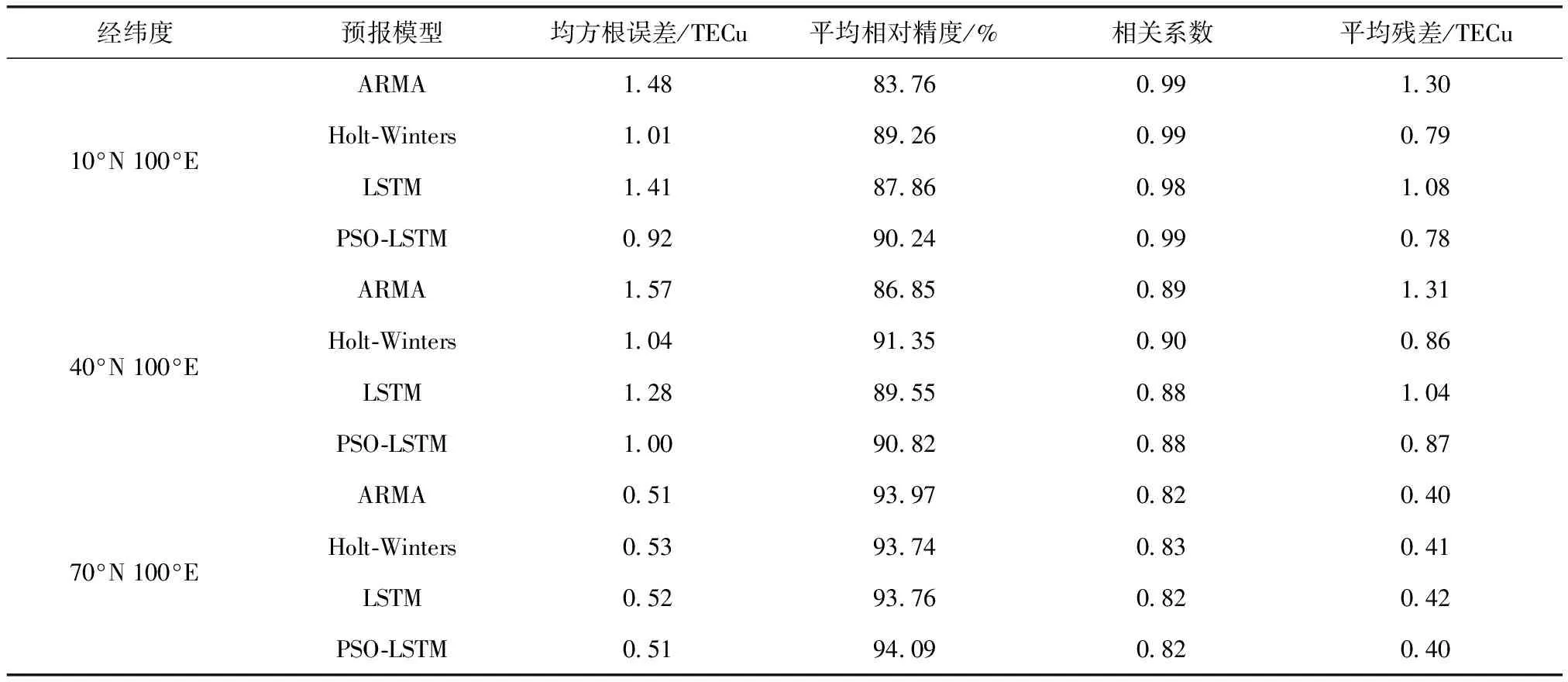
表1 年积日177～181不同模型预报精度对比

从表中可以看出低纬度地区不同模型预报结果的相关系数高于中、高纬度地区，并且随着纬度的增加TEC预报值的相关系数呈现下降趋势。在均方根误差方面，不同模型在中纬度地区均方根误差最大，分别为2.29 TECu、1.72 TECu、1.91 TECu和1.76 TECu，高纬度地区均方根误差最小，为0.74 TECu、0.64 TECu、0.85 TECu和0.58 TECu。在平均残差方面不同模型在高纬度地区平均残差最小，分别为0.59 TECu、0.49 TECu、0.68 TECu和0.45 TECu。并且通过结合表1和表2，可以看出在不同季节、不同模型的预报精度有所不同，由于季节会对电离层TEC产生一定的影响，太阳活动剧烈的季节高纬度地区预报效果最差，经粒子群算法优化的LSTM神经网络在预报效果上有一定程度的提高，PSO-LSTM模型在太阳活动剧烈的季节高纬度的预报均方根误差相比LSTM模型降低了0.27 TECu，平均相对精度提高8.82%，相关系数提高0.16，平均残差降低0.23 TECu，综合4个指标PSO-LSTM模型预报效果最优。

表2 年积日360～364不同模型预报精度对比

PSO-LSTM模型的预报残差如图4和图5所示，图4为太阳活动平静期不同模型的预报残差，图5为太阳活动剧烈期不同模型的预报残差。从中可以看出太阳活动平静期不同模型的预报残差均可保持在4 TECu 以内，其中PSO-LSTM模型预报残差最小，大多分布在2 TECu以内，ARMA模型的预报残差略大于Holt-Winters模型，LSTM神经网络的预报残差最大，低纬度地区部分残差超过5 TECu，是所有模型中预报残差最大的。太阳活动剧烈期不同模型的残差特点与平静期基本相同，PSO-LSTM模型和Holt-Winters模型残差较小，LSTM模型在某些时刻预报残差明显较大，在中纬度地区部分残差超过4 TECu。

图4 年积日177～181不同模型预报残差对比

图5 年积日360～364不同模型预报残差对比

为详细分析PSO-LSTM模型的预报效果，本次实验分别统计不同模型在年积日177～181的预报值残差分布情况如表3所示。从中可以看出PSO-LSTM模型在低、中、高纬度预报残差小于1 TECu,分别占比65.8%、65.8%和91.7%；ARMA模型在低、中、高纬度预报残差小于1 TECu，分别占比36.7%、43.3%和92.5%；Holt-Winters模型在低、中、高纬度预报残差小于1 TECu，分别占比68.3%、60.8%和94.2%；LSTM模型在低、中、高纬度预报残差小于1 TECu，分别占比57.5%、52.5%和93.3%。3个纬度4种模型小于1 TECu的预报残差取平均后分别为74.4%、57.5%、74.4%和67.8%，其中PSO-LSTM模型预报残差小于1 TECu的占比最高。

表3 年积日177～181不同模型残差百分比统计

年积日360～364不同模型的预报值残差分布情况如表4所示，PSO-LSTM神经网络模型在低、中、高纬度预报残差小于1 TECu约占59.2%、40.8%和95%；ARMA模型在低、中、高纬度预报残差小于1 TECu约占54.2%、30%和81.7%；Holt-Winters模型在低中高纬度预报残差小于1 TECu约占47.5%、45%和92.5%；LSTM模型在低中高纬度预报残差小于1 TECu约占52.5%、46.7%和74.2%；不同模型小于1 TECu的预报残差取平均后分别占比65%、55.3%、61.7%和57.8%。同时通过图4和图5也可以看出ARMA模型预报残差较大，LSTM模型和Holt-Winters模型次之，PSO-LSTM模型预报残差基本稳定在0左右，预报效果最为稳定。

表4 年积日360～364不同模型残差百分比统计

3 结束语

论文将粒子群算法引入电离层TEC预报模型，构建了一种PSO-LSTM神经网络模型，解决了神经网络预报模型的参数选择困难问题，将该模型与传统预报模型进行短期预报并评价其预报性能。实验结果表明，文中建立模型在实际的预报工作中具有自适应选取最优参数，自动高效得到最佳训练模型的优点，预报结果显示文中模型在太阳平静期的预报误差小于1 TECu；太阳活跃期预报误差小于1.8 TECu。与传统LSTM神经网络模型相比，文中模型在不同纬度的总体预报精度在太阳平静期提高了3.98%；太阳活跃期提高了8.48%，与单一模型相比PSO-LSTM神经网络模型预报的精准度和稳定性均有提升。将粒子群算法应用于电离层监测预报领域为模型的优化改进提供了一个新的思路。