鄱阳湖圩堤漫顶可靠度分析——以沿河圩为例

涂宜昌，雷 声，孙东亚

（1.江西省水利科学院，江西 南昌，330029；2.河海大学水利水电学院，江苏 南京，210098；3.中国水利水电科学研究院，北京，100038）

0 引言

鄱阳湖区现有千亩以上圩堤420座，堤线总长3 563.6km，承担着抵御洪水侵害、保护湖区工农业以及人民生命安全的重要责任[1，2]。2020年鄱阳湖大洪水，湖区圩堤发挥了显著的防洪减灾作用，但圩堤在洪水期出现多处险情，超历史的大洪水使圩堤漫顶的风险尤为严重[3，4]。因此，合理的圩堤漫顶风险分析是必要的，不仅对圩堤后期的除险加固具有指导作用，而且能进一步提高圩堤的应急管理水平。

国内堤防溃决原因主要有漫顶、渗透破坏和失稳，其中漫顶失事的比例最高，有学者也对堤防漫顶可靠度方面进行过相关研究。王靖文等[5]通过拟合河流水位函数，分析其中参数分布规律，并基于卡洛蒙特模拟建立堤防漫顶失效概率计算模型，得到河流水位与可靠度的关系。李志龙等[6]通过分析堤防漫顶失事模式，通过洪水位的皮尔逊Ⅲ型分布，建立堤防的漫顶可靠度计算模型。陈东初等[7]基于JC法建立堤防漫顶风险模型，并研究三峡水库运行对其漫顶可靠度的影响。相关模型和数学方法在堤防漫顶可靠度研究方面取得了不错的成效。

本文以鄱阳湖区沿河圩为例，总结堤防漫顶风险内涵，在可靠度理论的基础上，建立沿河圩圩堤漫顶可靠度计算模型，分析圩堤漫顶可靠度与设计洪水位、服务年限和风险损失系数的关系，从而得出沿河圩漫顶可靠度整体情况。

1 工程概况

沿河圩属江西省上饶市鄱阳县管辖，位于饶河尾闾，昌江与乐安河交汇处北岸。圩堤始于鄱阳县湖城大桥上游朱家村，经鄱阳大桥至鄱阳中学，接青山圩止于双港桥下村，堤线总长度14.75km。工程保护面积30.35km2，保护耕地1 040hm2（1.56万亩），保护人口14.92万人。保护区是全县政治、经济、文化和交通中心。2020年鄱阳湖大洪灾，沿河圩受灾严重，累计发生2处滑坡险情，3处渗水险情，1处漏洞险情以及1处穿堤建筑物险情。

沿河圩始建于1968年，为鄱阳湖区重点圩堤，后通过鄱阳湖区二期防洪工程第五个单项工程于2005年进行过一次除险加固，为4级堤防工程，其防洪标准为：饶河尾闾区堤段为20年一遇洪水，湖盆区堤段为鄱阳湖相应湖口22.50m（吴淞高程）洪水位，穿堤建筑物设计洪水位比所在堤段设计洪水位提高0.5m。沿河圩设计堤顶宽度6.0m，土堤段迎水坡、背水坡设计坡比均为1:3.0，堤顶安全超高1.5m。

2 漫顶可靠性分析

2.1 堤防漫顶风险内涵

堤防是保护人民生命安全的重要屏障，其防洪标准是堤防设计的一个重要指标[8]，一般以重现期的形式表示。由于洪水的随机性，堤防任何防洪标准都有可能被洪水超过，堤防的漫顶风险由此产生。而堤防漫顶主要原因有洪水位过高、风浪大和安全加高不足等[9]。

总而言之，堤防漫顶失事是指洪水位没有超过堤防顶部，但是在风荷载的作用下，水面产生风浪壅高和波浪爬高，越过堤顶对堤坡造成冲刷破坏，而洪水漫溢是洪水直接超过堤顶，对其进行冲刷破坏[10]，堤防漫顶示意图如图1所示。

图1 堤防漫顶示意图

2.2 圩堤漫顶可靠度模型构建

根据可靠度理论，结构的极限状态可由功能函数g表示，在工程应用中，大多数情况，功能函数与荷载S和抗力R有关，表示为

由（1）式可知，当Z＞0时，结构安全，则结构可靠概率Pa为

式中：s为荷载S的变量；r为抗力R的变量；（fr，s）为变量s与变量r的联合概率密度函数。

在漫顶失效模型中，洪水是否能漫顶是由洪水位h、风壅高度e、波浪爬高hs决定。由其风险含义可知，极限状态功能函数为Z=h0-h-e-hs=0（h0为堤顶高程），但是其联合概率密度函数（fr，s）很难得到，又因为h与水文中的洪水频率曲线有关，e和hs由设计风速V决定，而V又与风速重现期Tw有关，所以，当h+e+hs＜h0时，认为堤防是安全的，也认为堤防的可靠度就是此事件发生的概率，即

式中：P1为洪水位h小于设计洪水位hf事件发生的概率；P2为实际风速v低于设计风速V事件发生的概率。两事件发生是相互独立的。

在堤防失事概率分析中，缺少洪水资料的情况下，洪水频率曲线作为洪水位概率密度函数，可以考虑采用皮尔逊Ⅲ型分布、极值Ⅰ型分布或者更简单的指数分布，以指数分布为例，洪水位概率密度函数为

式中：λ为指数分布的参数且λ＞0。

洪水位概率分布函数F（h）为

则洪水位小于设计洪水位的概率P1可以表示为：

根据前人研究[11]，采用泊松分布评估堤防漫顶可靠度，且不考虑水力方面不确定性，P2可用下式表示

式中：t为服务年限，年；Tw为风速重现期，年。P2表示风速重现期Tw的设计风速不超过服务年限t的设计风速的概率。

实际上，风浪越过堤顶并不意味着堤防一定会溃决失效，只能说堤防有一定失事的可能性，而计算这个可能性的大小是一个复杂的问题，为简化计算过程，引进一个风险损失系数w。w表示风浪越顶对堤防失事的贡献能力，是一个权重系数，取值在0到1.0之间，而影响w取值的因素包括堤坡坡度、堤身材料、水力冲刷程度等[12]。则P2最后表示为

则堤防漫顶可靠度Pa最后由（6）与（8）式相乘得

2.3 风速重现期推算方法

依据我国的《堤防工程设计规范》[13]，风壅高度e计算公式为：

式中：K为综合摩阻系数，可取3.6×10-6；V为设计风速，m/s；F为计算点逆风向量到对岸的距离，m；d为水域平均水深，m；β为风向与堤轴线的法线的夹角，°；g为重力加速度，取9.8m/s2。

hs为波浪爬高，可以依据前人研究的经验公式计算[11]，则

式中：hl为有效波高，m；L 为波长，m；Fe为有效吹程，km；V 为设计风速，km/h。

式中：a、b为系数，根据坡度取值，具体参考文献[11]。

在风险分析中，最大风速的概率分布为最大值分布，一般采用极值Ⅰ型分布，则设计风速与风速重现期的关系为[10]

式中：α和μ为分布系数；E（V）为最大风速的均值；σ（V）为最大风速的标准差。

对于已建的堤防工程，已知堤顶超高Y，当e+hs-Y＞0时，风浪越顶，即视堤顶超高值为风壅高度和波浪爬高之和的临界值，则可通过堤顶超高（10）、（11）、（12）和（13）式推算设计风速，再以（14）、（15）和（16）式推求风速重现期。

3 漫顶模型在沿河圩的应用

3.1 设计风速重现期

以沿河圩湖盆区堤段为计算对象。对于风壅高度e，假定F为12 000m，d为 15m，安全起见 β为 0°；对于波浪爬高 hs，假定 a为 4.5，b为 8.6，Fe为 12km。联立四式解得，设计风速V=23.6km/h。

假设 E（V）=19.8km/h，σ（V）=8.2km/h，则可以得到设计风速与设计风速重现期的关系，Tw=85.3年。

3.2 圩堤可靠度

通过文献[14]可知，鄱阳湖实施退田还湖后，湖口站100年一遇的洪水位为23.0m，通过（4）式可得到λ=0.1。假定圩堤的服务年限t分别为10、20、50、100年，风险损失系数 w 分别为 0、0.2、0.5、0.8、1.0，而 w 为 0 和 1.0分别代表风浪越顶无影响和风浪越顶堤防直接失事两种情况，则沿河圩堤湖盆段漫顶可靠度与设计洪水位的关系如图2所示。

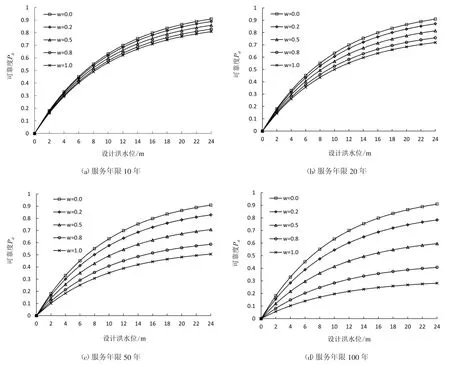
图2 不同服务年限条件下可靠度与对比图

根据以上成果，当hf=22.50m且Tw=85.3年时，沿河圩堤湖盆段漫顶可靠度与服务年限的关系如表1。

表1 沿河圩堤湖盆段可靠度

3.3 圩堤可靠度与影响因素的关系

根据圩堤可靠度计算模型，可靠度与设计洪水位、服务年限和风险损失系数有关。根据图2结果，可靠度与各因素关系分析如下：

（1）在不同服务年限与不同风险损失系数的各种组合下，可靠度与设计洪水位关系曲线呈现出相似的变化趋势。可靠度随设计洪水位的升高而增大，同时可靠度增大的速度随设计水位升高而减小，可靠度值不断增加并趋于平衡，这说明设计洪水位提高到一定程度后，对可靠度的影响力度会显著降低。所以，合理提高防洪标准，有利于可靠度的提升。

（2）在不计风险损失系数为0的理想情况下，在同一设计洪水位和风险损失系数下，圩堤的可靠度随服务年限的增加而减小，而服务年限是风浪对圩堤可靠度影响的另一种表现形式。这说明风浪对可靠度存在较大的影响，则可以考虑增加防浪墙高度，来提升圩堤可靠度。

（3）在同一设计洪水位和服务年限下，圩堤的可靠度随风险损失系数的增加而减小。而且随着服务年限增加，不同风险损失系数的曲线之间的差异变大，进而影响可靠度大小，这是由于风险损失系数是通过削弱风浪的作用来影响圩堤可靠度的。这也说明风险损失系数的取值对可靠度有很大的影响，可以考虑取不同风险损失系数下可靠度的均值，削弱其影响。

3.4 沿河圩漫顶可靠度情况

当Pa≥0.9时，视为圩堤漫顶安全性良好；当0.9＞Pa≥0.8时，视为圩堤漫顶安全性合格；当0.8＞Pa时，视为圩堤漫顶安全性不合格。从表1可知，对沿河圩来说，在风浪完全无影响的情况下，沿河圩可靠度最高只达到0.895，未超过0.9，圩堤漫顶安全性未达到良好，这说明原有防洪标准hf=22.50m偏低。

以其不同风险损失系数均值代表相应服务年限的可靠度，沿河圩服务年限为20年的可靠度为0.801，圩堤漫顶安全性刚好合格，在预期服务20年以后，可靠度小于0.8，圩堤安全情况不合格，预期服务20年应为沿河圩漫顶可靠度合格的临界年限。而沿河圩从上一次2005年除险加固到现在，已运行使用16年，由（9）式计算不同风险损失系数下的可靠度，得其均值为0.818，虽然沿河圩距临界年限还有一段时间，但可靠度的富裕度较少，沿河圩漫顶安全性勉强合格。

综上所述，沿河圩原有防洪标准偏低，而且其可靠度富裕度较少，随着运行年份的增加，其圩堤可靠度势必很快变为不合格，所以在沿河圩的除险加固方面，建议合理加强其防洪标准，加高其防浪墙高度，从而提高其防洪能力和漫顶可靠度。

4 结论

本文基于可靠度理论，构建圩堤漫顶可靠度计算模型，结合鄱阳湖沿河圩进行模型应用，重点针对漫顶可靠度进行研究，具体结论如下：

（1）设计洪水位、服务年限和风险损失系数等因素对圩堤漫顶的可靠度都有很大程度的影响，一般圩堤可靠度随设计洪水位升高而增大，随风险损失系数或者预期服务年限的增大而减小。

（2）沿河圩漫顶可靠度最高为0.895，未达到良好的标准，原有防洪标准偏低，而且沿河圩距上次除险加固已有16年，其可靠度均值为0.818，高于0.8，但可靠度富裕度较少，圩堤漫顶安全性勉强合格。

（3）在沿河圩除险加固方面，建议合理提高其防洪标准和加高其防浪墙高度。