基于压缩激励残差神经网络的轴承损伤诊断*
2022-04-06韩元政谷艳玲陈长征孙鲜明
韩元政 谷艳玲 陈长征 田 淼 孙鲜明
1沈阳工业大学机械工程学院 沈阳 110870 2宁波坤博测控科技有限公司 宁波 315201
0 引言
滚动轴承作为各类型旋转机械设备的主要部件,其稳定运行对于设备而言是至关重要的[1]。当轴承在运转过程中出现损伤,不仅会造成经济损失,更严重的会导致人员伤亡。随着轴承损伤诊断技术的不断发展,若轴承出现损伤状况,解决流程是先对轴承的损伤信号进行采集,然后对其进行损伤特征提取,最后对损伤类型进行识别[2]。轴承损伤特征提取的方法主要包括傅里叶变换、局部均值分解和变分模态分解等[3]。对于轴承损伤识别的方法主要有支持向量机、极限学习机等机器学习识别方法和前馈神经网络、卷积神经网络以及卷积神经网络变体等[4]深度学习识别方法。
由于轴承损伤特征提取的轴承振动信号大部分都是非平稳的信号。时频分析弥补了单一使用时域分析和频域分析的不足,能更好地反应轴承损伤信号的细节[5],是处理非平稳信号的有力工具。连续小波变换是时频变换的一种,能减小信息冗余,适合相似性检测和奇异性分析,且能很好地显现出轴承损伤信号的时频特性。
残差神经网络(ResNet)是He[6]提出的新型网络结构模型,其在传统的卷积神经网络结构中引入残差学习,加速了模型训练的速度,提高学习效率。将压缩激励(SE)模块引入到残差神经网络中,相较残差神经网络极大地提高了模型的准确率,且模型的训练速度更快。目前国内学者对压缩激励残差神经网络进行了大量研究,罗会兰等[7]运用压缩激励残差模型对视频动作进行识别,实验证明了该方法能有效地提升动作识别性能。邬可等[8]运用压缩激励残差神经网络与行人的特征进行融合,进而对人进行重识别,相比于其他神经网络模型具,实验证明其有更高的精度。
本文针对轴承运行产生的损伤问题,提出了基于压缩激励残差神经网络的轴承损伤识别方法。该方法首先对轴承原始振动信号用连续小波变换(CWT)进行时频变换,生成二维时频图像样本;再将样本送入压缩激励残差神经网络模型进行训练;最后在输出层使用Softmax分类器对轴承损伤类别进行分类,并用实验台对模型性能进行测试。为验证模型的效果,分别对不同特征提取方法和不同网络模型准确率设置了2组对照试验。实验结果表明:使用压缩激励残差神经网络前提下,连续小波变换相比于振动灰度图(VI)和短时傅里叶变换(STFT)诊断用时短、准确率高。将连续小波变换后的时频图像样本作为输入,压缩激励残差神经网络模型相比于其他神经网络模型具有更高的轴承损伤识别精度。
1 轴承损伤诊断方法的基本理论
1.1 连续小波变换
连续小波变换是时频分析方法之一,其自适应主要体现在窗口大小由频率高低自动调整,能够进行多分辨率分析[9]。连续小波变换表达式为
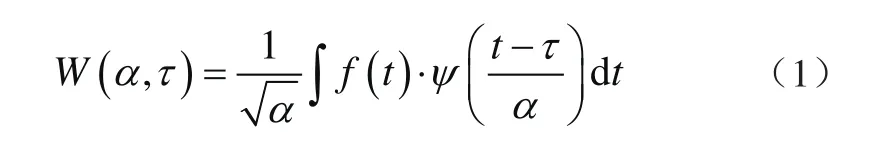
式中:α为尺度因子,τ为平移因子,α为控制小波变换的中心频率,τ控制小波在时间轴沿着信号的平移。两参数因子由母函数ψ(t)经过伸缩平移得到,且均取连续变化值。连续小波变换能有效显示信号特征。
1.2 压缩激励模块
压缩激励模块如图1所示,压缩激励模块分为压缩和激励2部分。压缩部分(Squeeze)是用全局平均池化的方法将维度为H×W×C的特征进行压缩,得到1×1×C,其中H为高度,W为宽度,C为通道数,经压缩后的H×W变为一维,这使得H×W的全局特征都赋给了压缩后的参数,使感受区域增大。激励部分(Excitation)为全连接层,将压缩部分的结果1×1×C作为输入,并对每个通道的重要性进行预测。Scale操作是将预测得到各通道重要性大小作用到之前的特征图所对应通道上[10],对提取的特征使用重标定的方法,并根据通道的重要程度得到权重。Scale操作极大提升了主要特征,使网络模型识别准确率得到了有效的提高。
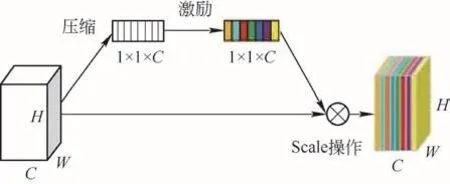
图 1 压缩激励模块
1.3 压缩激励残差神经网络
残差神经网络的出现解决了随神经网络深度加深而导致的网络退化等问题。在传统的卷积神经网络结构上加入带快捷连接线的残差块,由多个这样结构的网络块组成残差神经网络。残差块结构如图2所示。
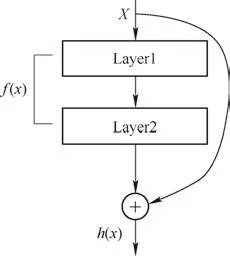
图 2 残差块结构
x作为网络的输入,h(x)为输出,若直接将x添加到网络的输出,则网络建模为f(x)=h(x)-x,称为残差学习。残差神经网络特点是可以让输入信息跳过当前网络层,直接传递到后面的网络层,有效地解决了随着训练网络层数的增加而导致网络效果变差等问题[11]。
由图3可以看出,压缩激励残差神经网络和残差神经网络很相似,但比残差神经网络做得更多。残差神经网络只是增加了一个跳跃链接,而压缩激励残差神经网络在其基础上,在相邻两个网络层之间加入了压缩激励模块,能使各通道之间的信息进行交互,大幅提高了网络的准确率。将压缩激励模块结合到残差网络结构中,能显式地表现出各特征通道之间的关系,并对提取的特征使用重标定的方法,进而根据通道的重要程度得到权重,即通过网络学习自动获取特征通道的重要程度,且根据每个通道重要程度的大小进行抑制或提升,相比引入新的空间维度极大地降低网络复杂度。
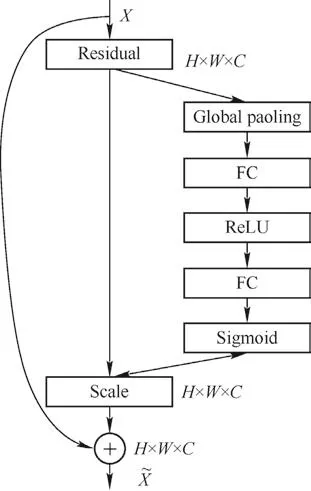
图 3 压缩激励残差神经网络结构
2 轴承损伤诊断方法
2.1 轴承损伤诊断流程
首先,对轴承原始振动信号进行重叠采样,并对截取的数据进行连续小波变换,得到包含轴承损伤特征的二维时频图像样本;其次,将压缩处理后二维时频图像样本输送到压缩激励残差神经网络模型里进行训练和损伤识别;最后,经过训练优化后的模型可用于轴承的损伤识别与分类。轴承损伤诊断流程如图4所示。
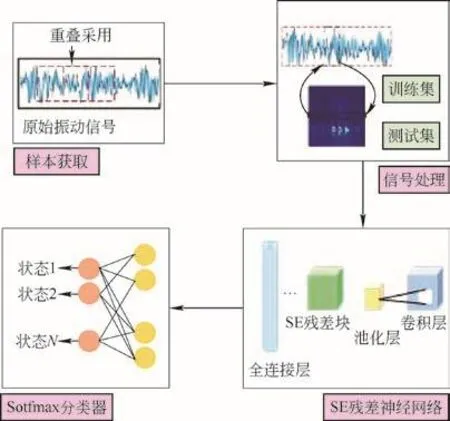
图 4 轴承损伤诊断流程图
2.2 模型参数设置
随着网络模型的深度增加,模型的特征学习能力也得到一定的提升。本文设计的压缩激励残差神经网络模型共38层,在压缩激励模块中添加BN层,并在网络结构中的全连接层用全局池化层替代,不仅减少模型的运算量,还增加模型的泛化能力。表1显示了压缩激励残差网络模型的结构参数。
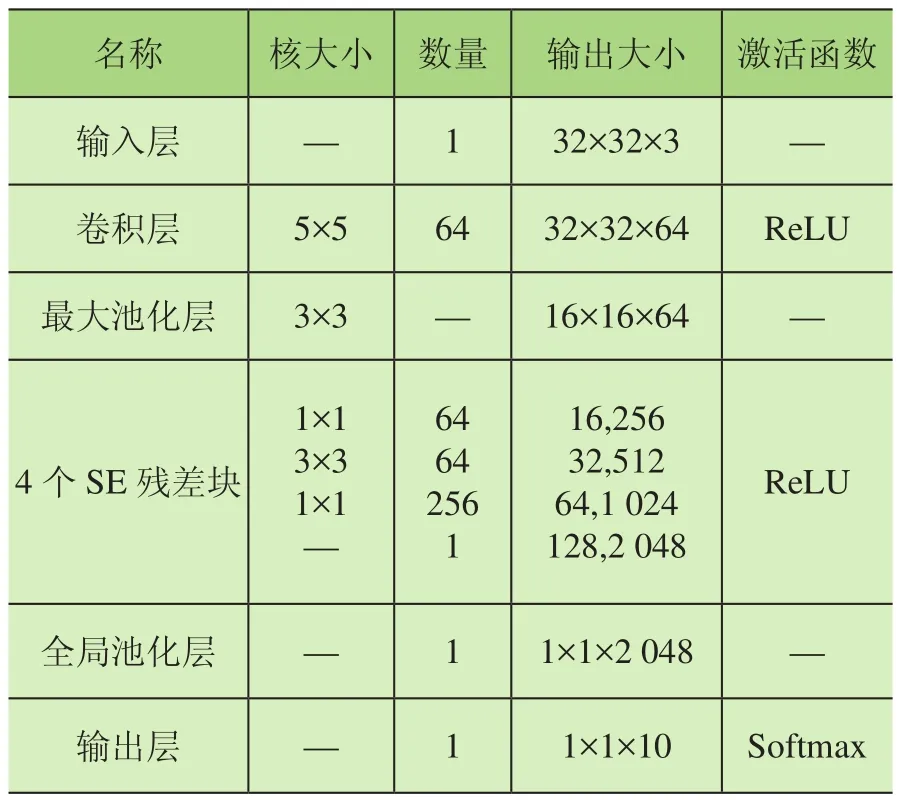
表 1 压缩激励残差神经网络结构参数
压缩激励残差神经网络结构主要包含1个输入层、1个卷积层、1个最大池化层、4个压缩激励残差块,1个全局池化层以及1个输出层。其中每个SE残差块结构中包含2个卷积层、1个全局池化层和2个全连接层。为了防止过拟合和梯度弥散等问题,在SE残差块结构中的卷积层后都引入BN层,不仅可以起到加速训练的效果,还能提高网络模型的泛化能力[12]。
4 实验验证
为验证实验结果,使用Inter Core i5-10400 CPU处理器、Window10系统的计算机,使用Matelab2018a、Python3.7进行编程,并在Tensor flow2.0的框架下进行实验。使用QPZZ-Ⅱ旋转机械振动损伤实验台的实际滚动轴承损伤数据进行验证。实验台如图5所示,其由交流电动机、加载装置、加速度传感器、速度传感器、转轴、测试轴承和VIBXpert振动数据采集器组成。利用振动数据采集器对测试轴承的水平和垂直方向的振动数据进行采样并实时传输到电脑中进行收集。

图 5 QPZZ-Ⅱ旋转机械振动损伤实验台
实验选用的轴承型号为NU205ECML圆柱滚子轴承,内径25 mm,外径52 mm,节圆直径38.5 mm,滚动体直径为7.5 mm,滚动体个数13,接触角0°。交流电动机转速为1 525 r/min,采样频率为16 384 Hz,损伤类型分别为轴承的滚动体损伤、内圈损伤、外圈损伤以及正常状态。通过振动数据采集器分别采集轻载和重载工况下4种损伤类型的轴承振动数据,并将标签设置为1~4,分别表示轴承4种损伤状态。实验数据集的划分是随机抽取总样本数据的2/3作为训练集,以总样本数据的1/3作为测试集,其中B代表滚动体、IR代表内圈、OR代表外圈,N代表正常状况,表2显示了轴承的损伤类型、标签和数据集的划分。
4.2 实验数据处理
本文选择轴承水平方向的振动数据,使用Matlab2018a对轴承原始振动数据进行处理。首先,考虑到数据样本有限,故采用重叠采样的方法增加数据量。其次,将轴承每种损伤类型的数据截成300段,每段截取信号长度为1 024。最后,使用连续小波变换对损伤信号进行时频变换,得到二维时频图像样本,图6为轴承轻载时的4种损伤类型的时频图像样本。其中,在对振动数据进行连续小波变换时,小波基函数的选取非常重要。常用的小波基有Haar小波和Morlet小波等,根据小波分析最大匹配原理,选取类似机械轴承脉冲信号的复Morlet小波的Cmor1-3作为母波,因为轴承振动信号与复Morlet小波的几何形状接近,所提取的特征准确,故尺度序列长度设置为256;其次,将时频图像压缩成大小;最后将压缩后的时频图像样本输入到压缩激励残差神经网络模型进行训练和测试。
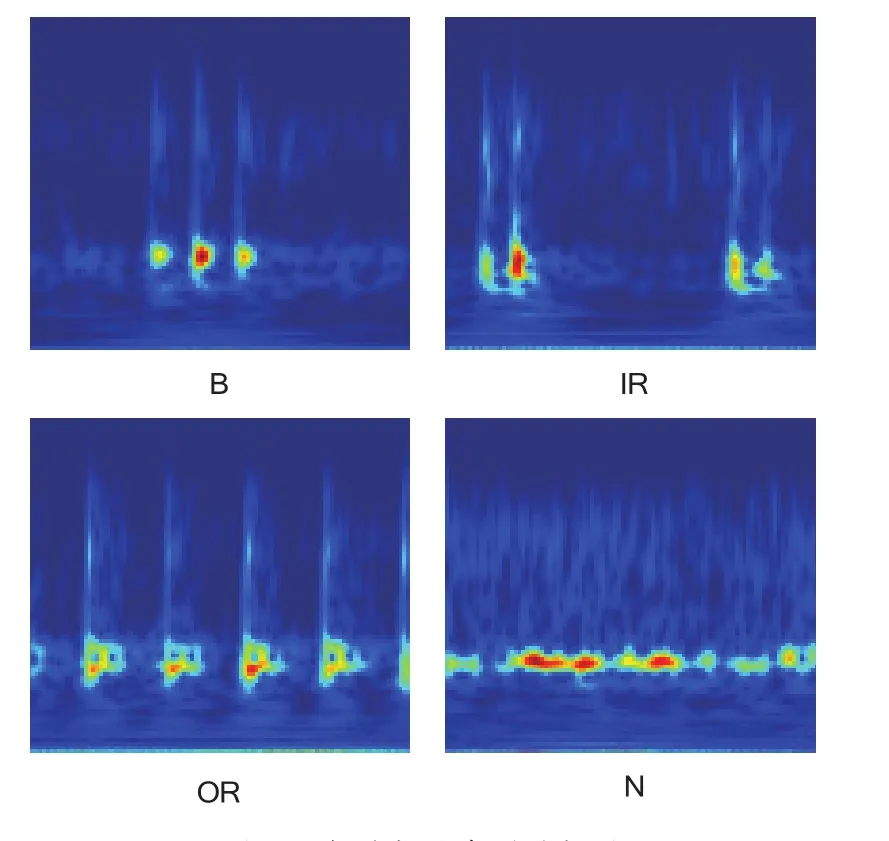
图 6 轴承损伤类型时频图
4.3 实验结果及分析
本文对实验台测试轴承数据分别使用振动灰度图、短时傅里叶变换、连续小波变换3种不同的数据处理方法进行比较,每种方法重复实验5次,以5次结果的均值作为最终结果,实验结果如表3所示。从实验结果中可以看出,3种不同的特征提取方法在压缩激励残差神经网络中,均能使损伤识别的准确率达到97%以上,实验证明这3种损伤特征提取方法的有效性和适用性。在均使用压缩激励残差神经网络前提下,连续小波变化相比于振动灰度图和短时傅里叶数据处理方式,训练时间更短,损伤诊断的准确率更高,故经对照实验结果选取连续小波变换作为轴承损伤诊断的数据处理方式。
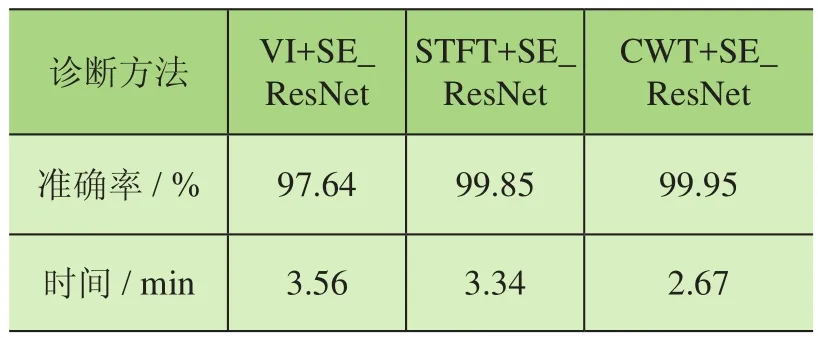
表3 基于压缩激励残差神经网络的诊断结果
为了验证压缩激励残差神经网络模型的优越性能,本文设计了另一组对照实验,将压缩激励残差神经网与卷积神经网络(LetNet),残差神经网络(ResNet),VGG进行对比。根据第1组对照试验结果,实验选用连续小波变换所得二维时频图像样本作为各神经网络的模型输入,经多次调试实验训练迭代次数均设置为10次。4种网络模型对比结果如图7所示。由实验结果可知,压缩激励残差神经网络相比于其他3个神经网络模型拥有更高的准确率。

图 7 神经网络模型性能对比
本文对压缩激励残差神经网络的结果进行分析,图8为压缩激励残差网络的损失曲线和准确率曲线,可知在迭代第4次时损失函数下降到最低且趋于稳定状态,准确率在迭代第4次时达到最高且趋于稳定状态。表明本文所设计的算法收敛速度快,准确率高,在轴承损伤诊断中具有良好的诊断效果。用混淆矩阵来进一步说明该模型,将实验的结果做成混淆矩阵如图9所示,每一行代表真实的分类结果,每一列代表测试的分类结果。由此可知,对角线代表所有类别预测的结果与真实结果的关系,其中,有1个轴承外圈损伤被错分为轴承内圈损伤,其他3种损伤类型的准确率都达到了100%。
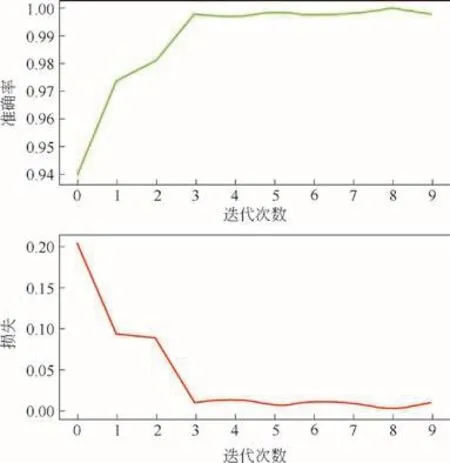
图 8 损失曲线和准确率曲线
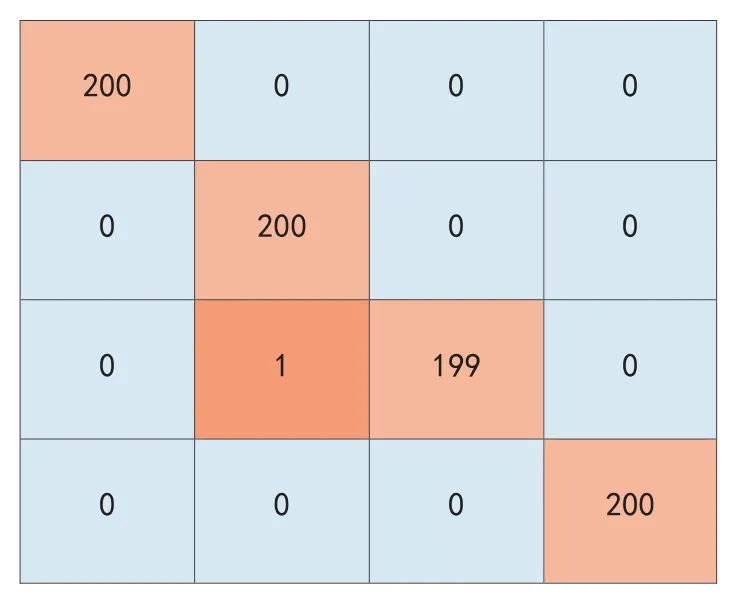
图 9 混淆矩阵
5 结论
本文针对滚动轴承损伤诊断问题,提出了一种基于压缩激励残差神经网络的损伤诊断方法,并运用实际滚动轴承实验台数据集对提出的诊断方法进行实验验证。同时设置对照实验,在选用连续小波变换的时频图样本作为模型输入的基础上,将压缩激励残差神经网络与卷积神经网络、残差神经网络、VGG网络算法的诊断准确率进行对比。实验结果证明了所提出压缩激励残差神经网络算法收敛速度快,对轴承损伤诊断的准确率高达99.95%。今后,将进一步优化损伤诊断模型,提升其损伤诊断的准确率,并将其应用于其他重要零件的损伤诊断中。
