基于前馈型神经网络解线性Fredholm积分-微分方程

许彩虹，邵新平，张 林

(杭州电子科技大学理学院，浙江 杭州 310018)

0 引 言

积分方程、积分-微分方程在解决数学，经济学和最优控制理论等方面应用广泛。这些方程一般无法直接求得精确解，通常采用不同的数值方法进行近似求解。目前，许多先进而有效的数值方法被用于求解积分方程。例如，文献[1]用Taylor展开式求解积分方程，文献[2]引入了Taylor矩阵法求解积分方程，文献[3]提出求解Volterra积分-微分方程的He同伦摄动法，文献[4]对求解线性Fredholm积分方程的同伦摄动法进行了改进，文献[5]应用Legendre多项式求解高阶线性Fredholm积分-微分方程的混合条件，提出了Legendre配置矩阵法。神经网络在求解积分-微分方程领域也取得了一些进展，文献[6]将神经网络模型应用于求解Lyapunov矩阵方程，文献[7]将深度神经网络模型用于求解高维椭圆型偏微分方程。本文提出了一种基于Taylor展开式的神经网络解线性Fredholm积分-微分方程的新方法，采用Taylor展开式代替原系统中的未知函数，构造一个两层的前馈神经网络，经过神经网络学习得到相应的数值解。

1 积分-微分方程

1.1 Fredholm积分-微分方程

线性Fredholm积分-微分方程的基本形式为：

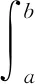
(1)

式中，λ>0，k(s,t)为a≤s,t≤b上任意给定的一个核函数，f(t)为t∈[a,b]上的函数，f(t)和k(s,t)均为已知函数，而F(t)为未知函数。

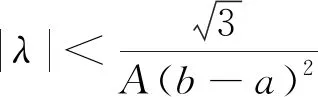
证明先证存在性。对式(1)两边同时在区间[a,t],a≤t≤b上取积分，得到：

(2)

构造皮卡逐步逼近序列{Fn(t)}：

(3)

f(t)在a≤t≤b内连续，则F0(t)有界。令F0(t)≤F，可得:

依次类推，可得：

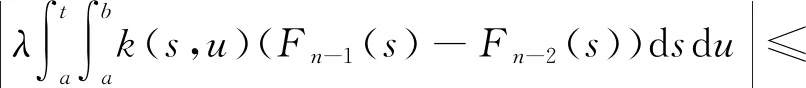
由魏尔斯特拉斯判别法可知，序列{Fn(t)}一致收敛。

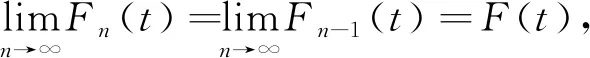
再证唯一性。设G(t)是方程(1)的另一个解，则

(4)

由式(2)—式(4)可得

应用柯西布尼柯夫斯基-施瓦茨不等式，可得：

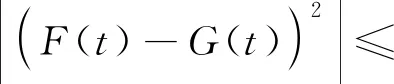
两边同时取定积分，得到：

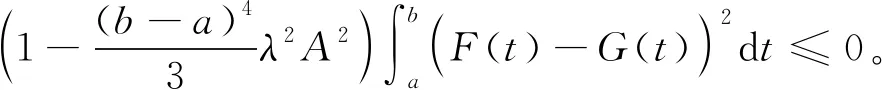
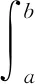
1.2 Fredholm积分-微分方程的线性方程组

第二类Fredholm型积分-微分线性方程组的一般形式如下：

(5)

式中，t,s∈[a,b]，Aji(t),kji(t)为实函数，并且假定Aji(t),kji(s,t)在区间a≤s,t≤b上对于所有的参数都是可微的，F(t)=[F1(t),…,Fn(t)]是待确定的向量解。

1.3 Fredholm积分-微分方程的Taylor展开

为了简单说明Fredholm积分-微分方程的Taylor多项式方法的基本原理，取n=2，即：

(6)

则给定系统解的形式为：

(7)

对式(6)的每个方程进行N-1次关于t的微分，得到：

(8)

(9)

式中，

2 神经网络构造与学习算法

2.1 输入输出关系

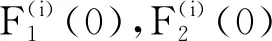
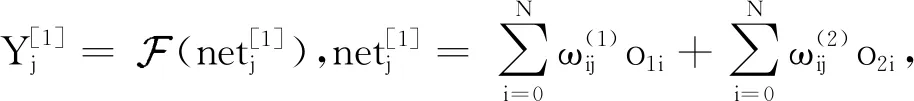
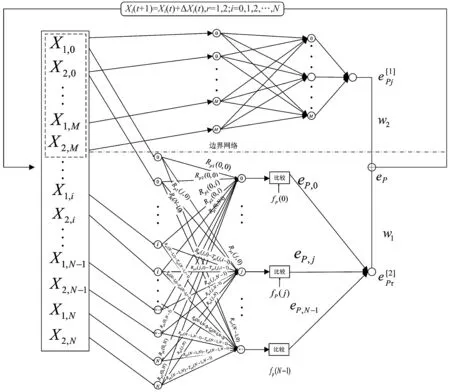
图1 神经网络示意图

2.2 误差函数

矩阵和目标向量的定义如下：

假设Yp=(Yp0,…,YpN)是对应于输入向量X1,X2的输出向量，Fpτ是Xpτ对应边界条件的输出向量，根据输入向量和输出向量定义误差函数，误差函数由内部误差和边界误差构成。

内部误差为：

(10)

边界误差为：

(11)

神经网络的总误差函数为：

(12)

式中，w1，w2表示内部误差与外部误差的权重，取w1=1，w2=1。

2.3 前馈神经网络学习算法

对输入信号Xri(r=1,2;i=0,1，2，…,N)进行随机初始化，初始值记为Xri(0)。

参数Xri的更新公式为：

Xri(n+1)=Xri(n)+ΔXri(n)

(13)

(14)

式中，n为迭代次数，α为动量项常数，η为学习率。

前馈型神经网络(Feedforward Neural Network, FNN)算法的核心是通过式(12)中的成本函数计算出式(14)的导数。推导过程如下：

综上所述，FNN求解Fredholm积分-微分方程的算法流程如下。

(1)令α>0,η>0,Emax>0，随机初始化输入信号Xri。

(a)前向传播：通过输入向量计算输出向量;

(b)反向传播：利用代价函数来调整参数;

(c)通过将当前误差加到误差E中计算累积周期误差。

(4)如果E>Emax，将E设为0，返回步骤3开始一个新的训练周期；如果E≤Emax，终止训练。

3 数值实例分析

对Fredholm积分-微分方程进行数值求解，对近似解画出其误差曲线，并与梯形求积规则(Trapezoidal Quadrature Rule, TQR)数值方法进行比较。

取学习率η=0.01，动量项常数α=0.003，停止条件为E<10-8。求解下述线性Fredholm积分-微分方程组：

(15)

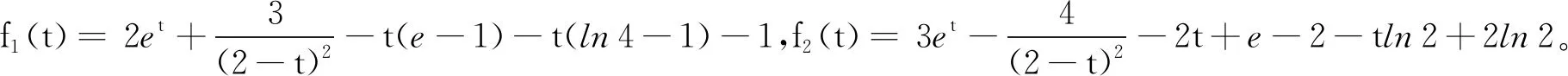
通过数值实例分析得到的近似解与误差分析如表1所示。从表1可得，使用FNN神经网络来近似求解方程组(15)，用四次多项式来逼近方程的解，经过255步，F1(t)和F2(t)的近似解为：

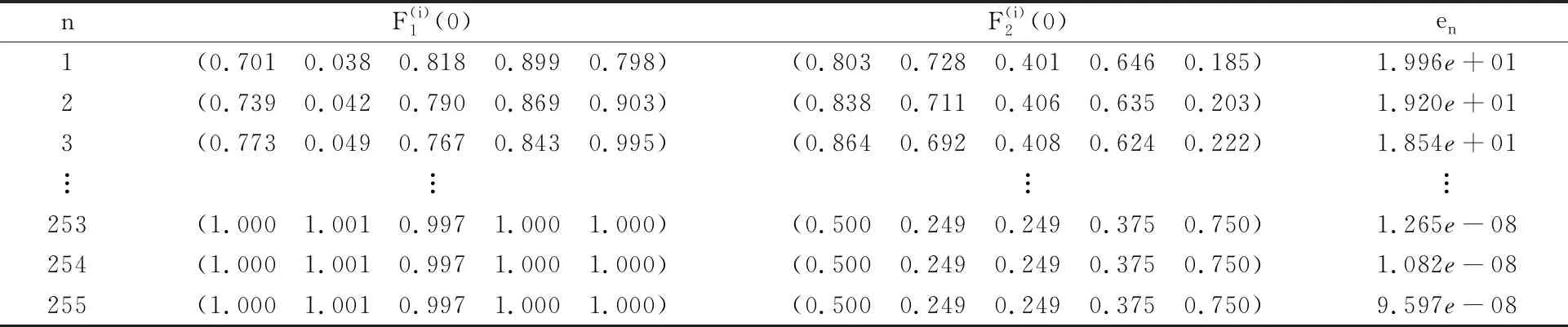
表1 近似解与误差分析表

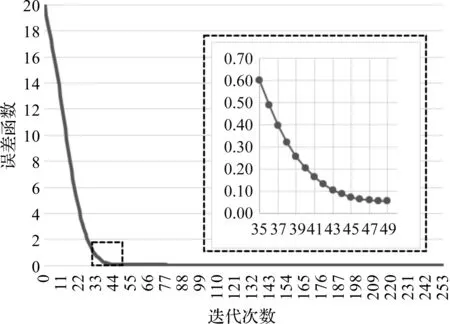
图2 误差函数与迭代次数的关系

误差函数与迭代次数的关系如图2所示。图2中，随着迭代次数的增加，误差函数迅速下降，最后趋于稳定。

近似解的收敛性如图3所示。从图3可以看出，迭代初期波动较大,这是由于随机产生初始值所导致，但随着迭代次数的增加，逐渐稳定并收敛到近似解。数值解与精确解的比较如图4所示。通过图4可知，Taylor展开式的阶数越高，精确度越高。

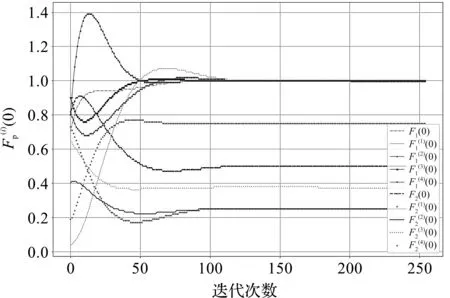
图3 近似解的收敛性

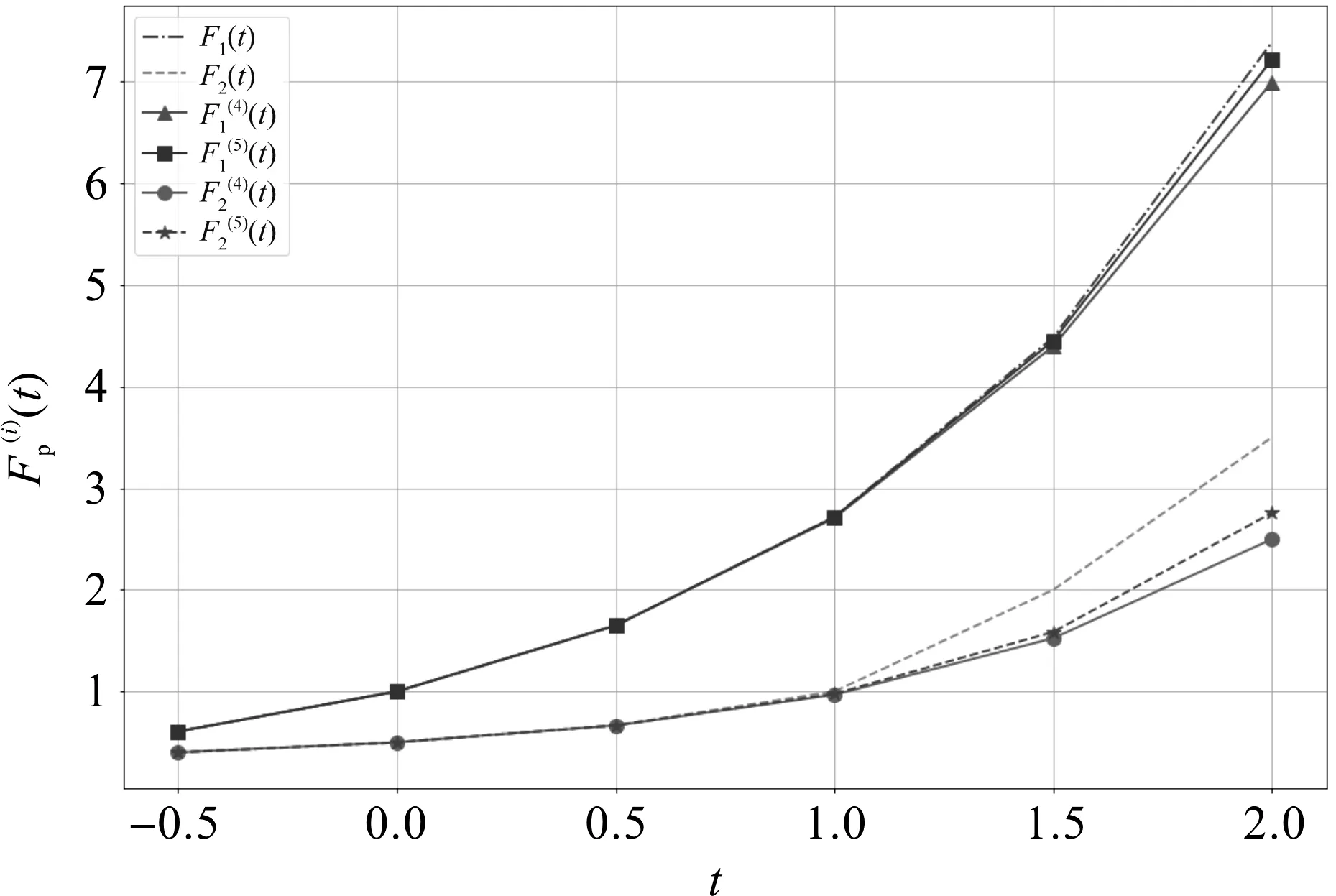
图4 数值解与精确解的比较

运用MATLAB R2014a实现算法求得线性方程组的近似解为：

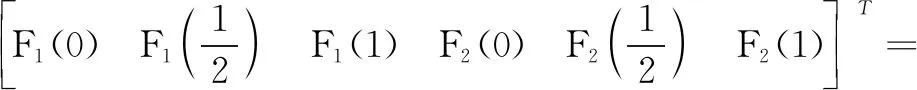
分别采用FNN算法和TQR算法来近似求解Fredholm积分-微分方程组(15)，2种算法得到的近似解与精确解如表2所示。通过表2中的数值对比可见，用FNN算法求得的近似解比TQR所得的近似解更接近精确解。

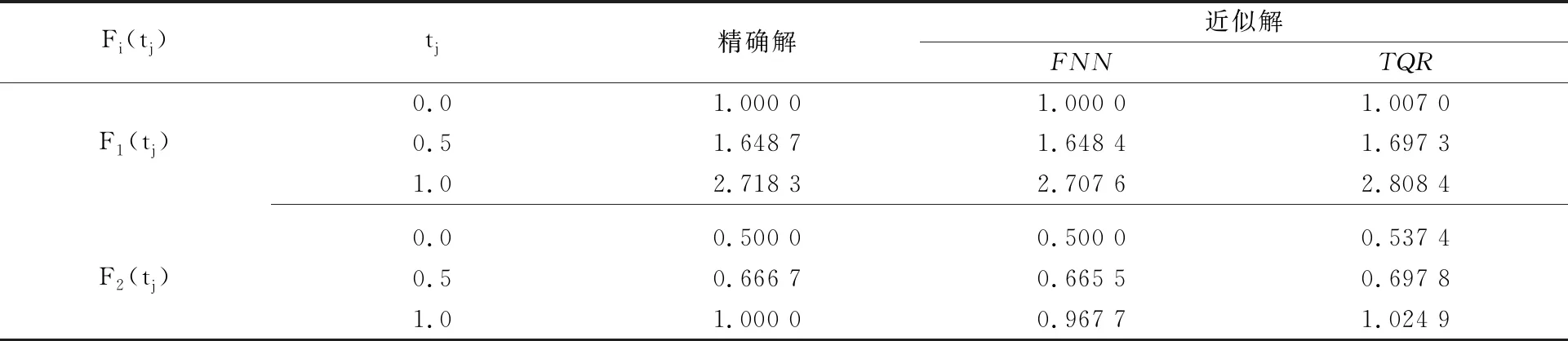
表2 近似解与精确解比较

4 结束语

本文提出一种基于神经网络近似求解线性Fredholm积分-微分方程的新方法，提高了算法的精确度。目前关于线性Fredholm积分-微分方程的相关研究较少，今后，将进一步拓展相关研究，采用其他方法用于求解线性Fredholm积分-微分方程，进一步提高算法的精度。