基于代理优化算法的岸桥轨道夹优化设计

余 镇,樊志华,李志华

(杭州电子科技大学机械工程学院,浙江 杭州 310018)

0 引 言

随着经济全球化逐步深入，港口贸易发展迅猛。岸桥作为装卸集装箱的主要设备，具有结构高、体型大等特点，也易受台风等恶劣天气的影响[1]。轨道夹是固定在岸桥底部的机械组件，为了防止岸桥滑动，轨道夹钳口直接与轨道接触，是轨道夹中受应力最大的零件。代理模型方法是解决复杂产品和系统优化设计问题的最有效途径之一，可以提高机械产品质量，节约成本。常见代理模型包括多项式回归模型、径向基回归模型、Kriging模型等。其中，Kriging模型能在给出预测值的同时给出预测偏差，成为最具代表性的代理模型[2]。张文丰等[3]采用Kriging代理模型方法修正了岸桥整体结构有限元模型，提高了岸桥的性能校核功能。LI等[4]提出一种关于岸桥结构模型验证和可靠性评估的综合框架，为岸桥可靠性评估提供科学依据。刘立成等[5]提出一种合理的湍流模型，提高了岸桥风载荷数值模拟的准确性，更好地模拟了优化岸桥结构在恶劣变化风载荷下的稳定性。设计合理高效的加点策略是代理优化算法的关键。JONES等[6]提出一种基于期望改进(Expected Improvement, EI)准则的有效全局优化(Efficient Global Optimization, EGO)算法，是最常用的加点准则。DONG等[7]使用多起点方法找到了代理模型的局部最优值，并在这些局部最优位置附近搜索全局最优解。HAO等[8]提出一种自适应多保真预期改进准则，以较少的分析调用提供最佳的优化结果。目前，现有的代理优化算法大多数关注无约束优化问题，应用范围受到一定的限制，对可行域边界的开发能力较弱[9]。SCHONLAU等[10]使用可行性概率(Probability of Feasibility, PoF)作为EI权重的约束加点准则，用于增强对可行域的探索。文献[11]结合PoF准则和EI准则进行双目标优化，开发了一类针对黑箱约束问题的并行优化算法。

岸桥轨道夹结构优化研究中，传统的结构优化方法一般采用经验公式进行计算，在定义复杂形状设计变量和防止网状失真方面效率较低，为此，本文基于Kriging代理模型，提出一种自适应约束代理优化算法，通过一个动态更新Kriging方法对轨道夹结构进行优化。

1 Kriging模型与代理优化算法

1.1 Kriging代理模型

Kriging代理模型为：

y(x)=μ(x)+Z(x)

(1)

式中，μ(x)为设计空间的全局模拟，反应总体变化趋势；Z(x)为均值为0、方差为σ2、协方差非零的随机过程，表示全局模拟基础上的局部偏差。

协方差矩阵和高斯函数如下：

(2)

Kriging代理模型未知点处的预测响应值为预测方差可以通过最小二乘法得到，有关Kriging代理模型的具体描述可参考文献[2,12]。

1.2 加点准则

1.2.1EI准则

Kriging代理模型不仅可以得到未知点处的预测响应值，还可以得到未知点处的预测标准差，EI加点准则结合了Kriging代理模型的这2个特点，表达式为：

(3)

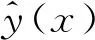
1.2.2 并行加点准则

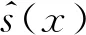
PEI函数表达式如下：

(4)

P函数表达式为：

(5)

式中，n表示加点的个数，本文取n=2；Nd表示设计变量的数目；Tc表示当前迭代步骤的相对时间，是先前迭代和当前迭代所添加样本数目与总预期样本数目之比；e-2.3026Tc表示优化过程中比例因子的衰减。

2 约束代理优化算法

本文提出的自适应代理优化算法结合改进的约束并行期望改进准则(Constrained Parallel Expected Improvement, CPEI)、重要边界采样准则(Importance Boundary Sampling, IBS)和约束函数Kriging模型更新策略。

2.1 约束处理

2.1.1PoF准则及CPEI准则

PoF准则计算样本点落在可行区域的概率，表达式如下：

(6)

由式(6)可知，PoF(·)是一个取值范围在0～1的联合概率密度。

将PoF准则作为EI准则权重的约束应对方法是现有文献中较常见的做法。同理，结合PoF准则，将式(4)中的ymin用最优可行解ymin_fea代替，根据PEI加点准则可以得到约束并行期望改进准则CPEI为：

CPEI(x)=PoF(x)PEI(x)

(7)

2.1.2IBS准则

IBS准则旨在解决黑箱约束函数问题，在距离当前设计点较小的约束区域内选择采样点。IBS值越大，当前采样点与约束函数之间的距离越小。在每个循环中，IBS准则都会选择该区域中IBS值最大的采样点。IBS函数表达式如下：

(8)

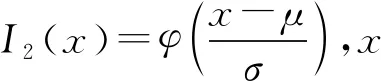
2.2 冗余点的删除

对于样本点的重复问题，可以通过高斯相关函数式(2)来判断。建立Kriging模型后，可获得2个样本点的相关性参数R，R∈[0,1]。R越接近0，2个点距离越大；R越接近1，2个点距离越小；当R=1时，2个点重合。

加入的样本点过度集中，容易造成样本点冗余，计算效率降低，为此，本文引入Euclidean距离E来删除相同样本点。

(9)

式中，xA表示通过加点准则选取的新样本点，xN表示加点前的样本点。若E<0.1，说明新样本点过度集中，删除加入的新样本点，否则可以添加新样本点。

2.3 约束函数Kriging模型更新判断方法

约束函数Kriging模型插值的不确定性可能会得到不可行的最优解，为此，本文引入一种客观的约束函数Kriging模型更新策略[13]。约束函数Kriging模型更新判断条件如下：

(10)

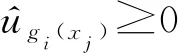
(11)

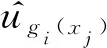
2.4 自适应约束代理优化算法流程

本文提出的自适应代理优化算法流程包括3个阶段。(1)第1阶段确定设计空间。使用拉丁超立方抽样方法得到样本库L，如果初始样本库L中没有满足约束条件的样本点，通过PoF准则添加1个可行样本点。(2)第2阶段通过IBS准则寻找离约束区域边界较近的样本点。受PoF准则的影响，CPEI准则更加倾向于在约束区域的中心区域取点，对约束边界区域的搜索能力较弱，故通过引入IBS准则来增强对约束边界的探索。同时，为了防止CPEI准则和IBS准则加入的样本点过于集中，通过Euclidean距离来判断是否删除新加入的样本点。两种加点准则均使用遗传算法寻优。(3)第3阶段在新增样本点附近，采用信任域法[12]进行取点，调用Kriging代理模型获得新增样本点目标函数、约束函数的预测响应值和预测误差，得到各信任域内满足约束函数Kriging模型更新条件的目标函数最小样本点，并通过仿真得到所需样本点的目标函数、约束函数真实值，加入样本库L，更新Kriging模型，直到满足终止条件，输出最优结果。

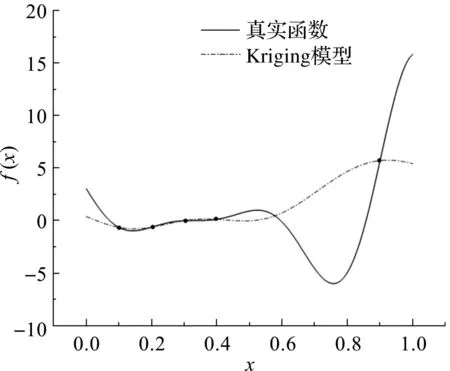
图1 一维函数Kriging曲线

3 算例分析

3.1 PEI加点准则的验证

为了验证PEI加点准则具有取得EI函数多个峰值点的特性，用一维函数进行验证。一维函数如下：

f(x)=(6x-2)2sin(12x-4),x∈[0,1]

(12)

初始采样点x分别取0.1，0.2，0.3，0.4，0.9，得到一维函数Kriging模型曲线如图1所示，P=1和P=2时的PEI函数分布情况如图2所示。

图2 PEI函数值分布曲线

从图2(a)可以看出，当P=1时，PEI函数与EI函数表达式相同，在x=0.14处得到最大峰值；从图2(b)可以看出，当P=2时，在x=0.63处得到最大峰值，并且和EI函数的第2个峰值点十分接近，接近图1中真实函数全局最优点。这是因为当P=2时，所有PEI函数值都被放大，而第2个峰值区域经放大后超过第1个峰值区域。综上分析可知，PEI准则具有寻找EI函数多个峰值近似区域的能力。

3.2 基于约束代理优化算法的函数优化

约束条件下的数学算例函数表达式为：

(13)

式中，x1,x2∈[0,1]。该函数的真实全局最优解为x*=[0.195 4,0.404 4]，对应真实最小值为0.599 8。函数在较大连通可行域内，存在一个全局最优点和多个局部最优解[3]，容易陷入局部最优区域，寻优困难。因此，这类函数需要更多的函数估值，算法的不同，对这类函数的寻优影响较大。

图3 3种优化算法的收敛曲线

通过拉丁超立方抽样得到10个初始样本点，分别使用本文算法、CEI单点加点准则和EI-PoF两目标约束并行加点准则优化算例(13)，一直加点至总样本数为60。每种算法分别重复运行20次，得到平均收敛曲线如图3所示，横坐标为样本点数，纵坐标为绝对误差A，A=|fmin(x)-freal(x)|，fmin(x)为函数最小值,freal(x)为真实最小值。

从图3中可以看出，本文算法得到的曲线收敛最快，到达收敛近似区域所用点数较小，迭代次数最少，且优化结果精度最高。

3种优化算法的函数优化结果如表1所示。

表1 3种优化算法的函数优化结果

从表1可以看出，和CEI及EI-PoF算法相比，本文算法的迭代次数分别减少了68.40%和36.80%；达到收敛所需样本数相差不大；绝对误差分别减少了48.17%和46.03%；计算时间最少，和CEI算法的差别比较明显。由此可见，本文算法的精度和效率最高。因为本文算法并行加点，减少了迭代次数，效率得到提高；加入CPEI准则和IBS准则探索未知点，精度也得到提高，验证了本文算法的可行性和有效性。

4 工程实例

4.1 港口集装箱起重机轨道夹模型

本文主要针对严重风负载条件下的钳口型轨道夹进行结构优化。轨道夹与轨道直接接触，使轨道夹与轨道夹紧或分离。文献[14]确定了对轨道夹钳口有重要影响的关键性结构参数，本文通过Solidworks软件，得到如图4、图5所示的三维模型，将钳口三维模型导入Ansys软件进行仿真分析，并通过静力学分析处理后，得到如图6所示的钳口有限元分析图。

图5中，变量的初始值设置为：结构厚度t1=30.0 mm，t2=30.0 mm，t3=30.0 mm，孔中心和曲率中心之间长度l1=30.0 mm，钳口的重量w=43.5 kg。图6中，初始设计区域产生最大应力σmax=545 MPa。钳口材料为42CrMo，屈服极限不低于823 MPa，根据欧洲起重机设计规范安全系数取为1.5，许用应力σa=549 MPa。

图4 楔形轨道夹三维模型

图5 轨道夹钳口三维模型

图6 钳口应力轮廓图

4.2 轨道夹的钳口结构设计优化

4.2.1 优化模型

选取t1，t2，t3，l1作为设计空间，以钳口受到的最大应力σmax为约束函数，以钳口质量w为目标函数，得到钳口结构优化数学模型：

minw(t1,t2,t3,l1)

(14)

4.2.2 钳口结构优化结果

通过拉丁超立方抽样得到21组样本点，采用Ansys软件进行仿真分析，部分结果如表2所示。

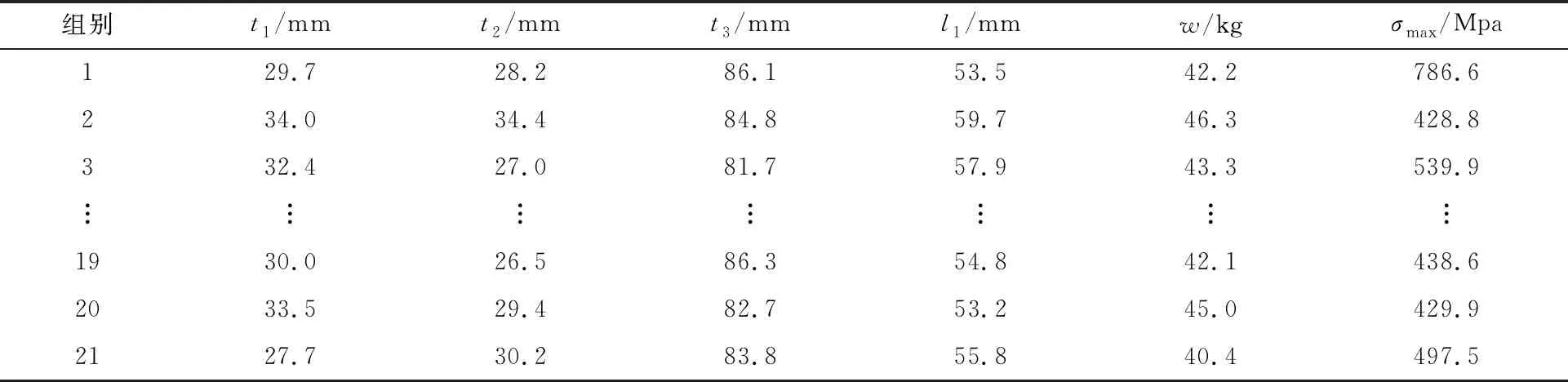
表2 21组轨道夹钳口结构样本数据

利用21组样本建立轨道夹钳口质量和应力的初始Kriging代理模型，分别采用本文算法、CEI算法和EI-PoF算法对Kriging模型不断优化加点，并及时更新Kriging模型，优化加点后获得最优解如表3所示。

表3 优化前后轨道夹钳口参数对比

从表3可以看出，采用本文提出的自适应代理优化算法对岸桥轨道夹钳口进行优化后，质量减少了13.1%，满足强度约束条件；对比CEI算法和EI-PoF算法，本文算法的优化次数最少，质量最轻，故优化效率更高，精度更好。

5 结束语

针对岸桥轨道夹优化过程中存在的问题，本文提出一种自适应约束代理优化算法。基于Kriging模型，结合IBS准则和CPEI准则，增加了对可行域边界的刻画，使得产生的样本点精确收敛于约束优化问题的真实最优解，有效减少了约束函数仿真次数，提高仿真效率；并在满足强度约束条件下，对岸桥轨道夹结构进行轻量化设计，解决了优化效率低的问题。但是，本文算法对复杂约束函数下最优解的搜索能力有所欠缺，后续将针对复杂约束下的函数最优解问题展开进一步研究。