非齐次Markovian跳变模糊系统的H∞控制

宋梦园，付世州，周绍生

(1.杭州电子科技大学理学院，浙江 杭州 310018；2.杭州电子科技大学自动化学院，浙江 杭州 310018)

0 引 言

在模糊控制工程中，区间二型模糊系统[1]解决了一型模糊系统隶属函数不确定问题，简化了计算复杂度，应用于众多工程问题。比如文献[2]采用一种基于区间二型模糊系统的算法解决了脑电图和脑计算机接口中的人工干扰问题。实际应用中，各种环境噪声及系统结构参数变化引起系统状态的突变，Markovian跳变随机奇异系统[3]应运而生。文献[4]研究无限状态下的Markovian跳变系统的稳定性问题，采用MATLAB中的LMI工具箱求得使系统指数稳定的状态反馈控制器的增益矩阵。文献[5]研究带有单维纳过程的奇异Markovian跳变系统的指数稳定性问题，在切换瞬间，使用投影引理，用一个微分方程将切换前与切换后联立起来，再根据Lyapunov第二稳定性理论给出系统在切换瞬间具有指数稳定性的充分条件，解决了切换瞬间状态跳跃不一致的问题。文献[6]研究带有噪声的不确定Markovian跳变奇异系统的鲁棒镇定和H∞控制问题，结合不等式放缩思想与Lyapunov稳定性理论得到系统具有无脉冲解且均方稳定的充分条件，并在此基础上求解状态反馈控制器的参数矩阵。文献[7]考虑Markovian跳变模糊系统在转移概率不确定时的情况，使用投影引理建立系统稳定的充分条件，采用锥补偿线性化算法求得广义耗散滤波器的参数。上述文献中，转移概率矩阵均为固定常数矩阵。但在实际应用中，转移概率难以保持稳定不变，通常是随时间变化的非齐次Markovian跳变系统。为此，本文研究连续时间上的一类非齐次随机奇异Markovian跳变随机奇异区间二型模糊系统的鲁棒H∞控制问题，采用分段齐次[8]的思想来处理转移概率随时间变化的特性，运用不等式放缩方法求解状态反馈控制器的增益矩阵，并给出系统满足H∞性能指标的充分条件。

1 系统描述

用IF-THEN规则描述的不确定随机奇异非齐次Markovian跳变模糊系统如下：

(1)

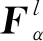
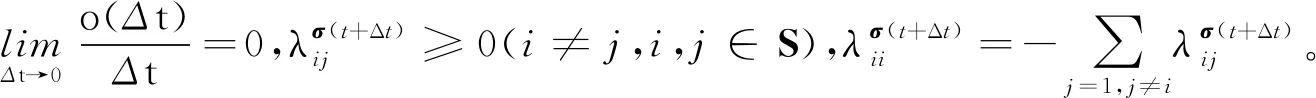
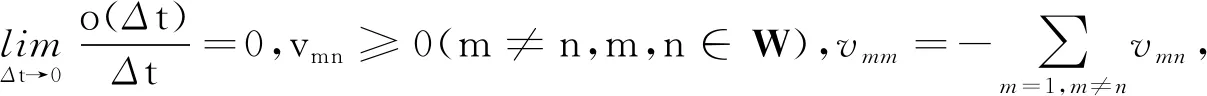
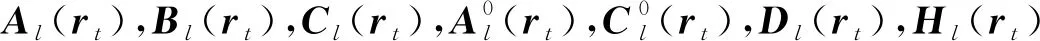
(2)

式中，Mi,N1i,N2i,N3i,N4i,N5i是适维常数矩阵，Fi(t)是未知的矩阵函数，且满足

Fi(t)TFi(t)≤I

(3)

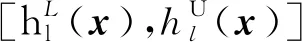
(4)

式中，

(5)

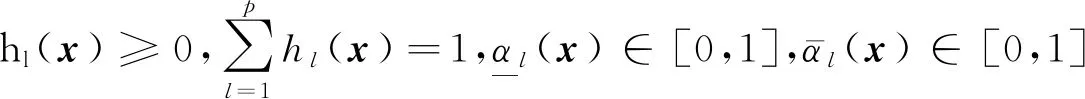
对于系统(4)设计一个前提不匹配的状态控制器，模糊规则如下：

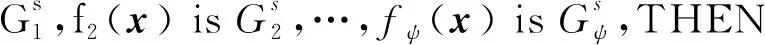
则全局模糊控制器为：

(6)

式中，

(7)

引理1[6]对于ε>0，若A,B,F,D,W是适维实数矩阵，且满足FTF≤I，则以下不等式成立：

(1)AFB+(AFB)T≤εAAT+ε-1BTB；

(2)(D+AFB)TW-1(D+AFB)≤DT(W-εAAT)-1D+ε-1BTB。

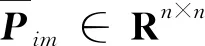
(8)

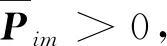
式中，U∈R(n-r)×n,V∈Rn×(n-r)分别是E的左零空间和右零空间的基，对称矩阵Pim∈Rn×n，非奇异矩阵Qim∈R(n-r)×(n-r)满足

(9)

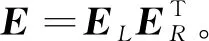
2 主要结果

(10)

(11)

式中，

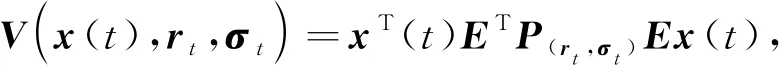
由伊藤公式的定义可得系统(4)的无穷小算子：

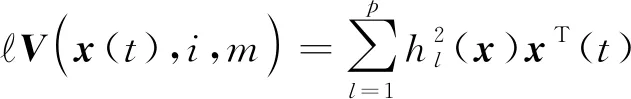
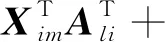
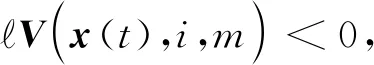
当v(t)≠0时，无穷小算子为：

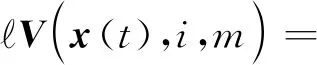
下面讨论系统在零初始状态下的H∞性能。用数学符号JT来表示H∞性能所需的条件，JT运算如下：

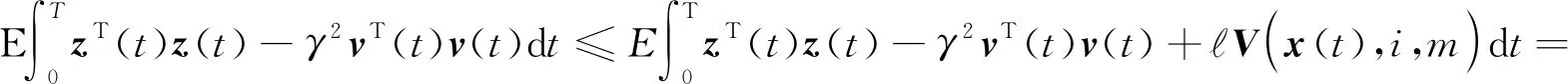
(12)

式中，H1im=(Ali+ΔAli)T(PimE+UQimVT)+(PimE+UQimVT)T(Ali+ΔAli)+

由引理1并结合不等式(11)，可得：

(13)

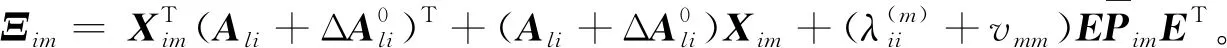
(14)

由Schur补引理可知，不等式(14)等价于式(12)，所以JT<0，说明系统(4)满足H∞性能指标，证毕。

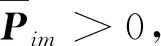
(15)

证明将控制器代入原系统可得闭环系统，可得：

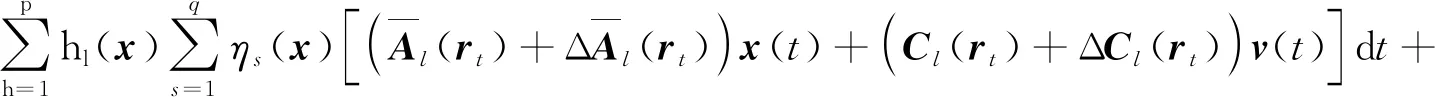
(16)

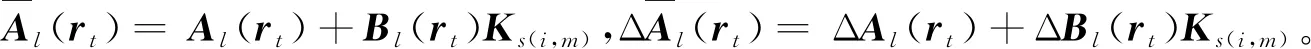
根据定理1可知，

(17)

式中，

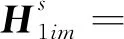
由Schur引理可知，不等式(17)等价于不等式(15)，故闭环系统(16)是随机稳定的。证毕。

3 数值示例

假设非齐次Markovian跳变奇异区间二型闭环系统中，l=2,s=2，其他参数如下：

γ=2.50,H22=-0.20。

其隶属度函数分别为：

根据定理2，采用MATLAB求得可行解为：

K122=[12.874 7 1.132 3],K211=[-10.944 5 4.338 0],K212=[-11.774 1 4.165 4],

K221=[3.098 0 1.536 7],K222=[4.526 2 1.450 8]。

使用MATLAB将所求可行解代入方程进行仿真，得到闭环系统状态响应如图1所示。图中，r(t),σ(t)表示系统模态切换的随机跳变过程。

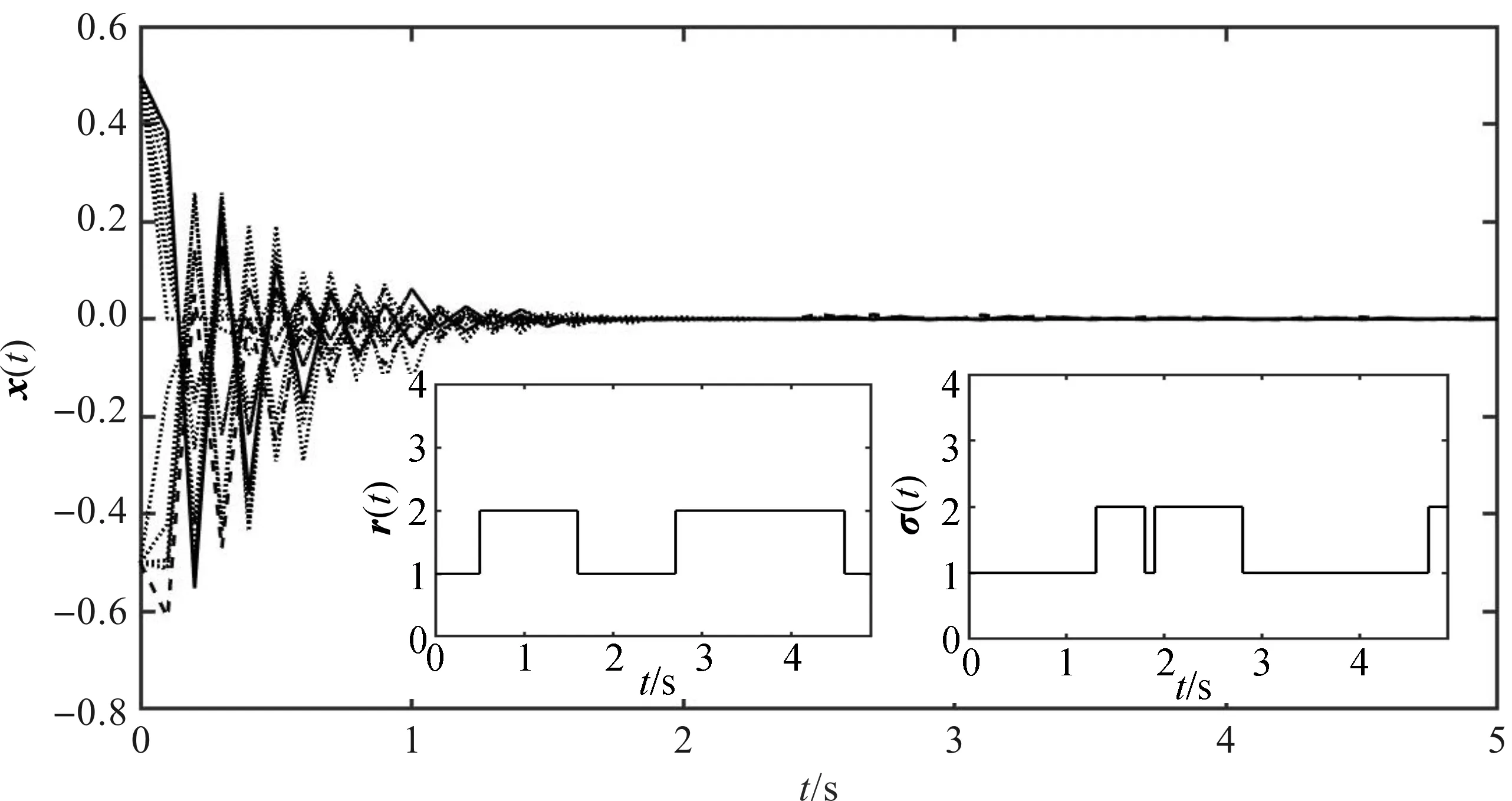
图1 闭环系统的状态响应x(t)

从图1可以看出，在随机跳变过程中，0～1 s时，闭环系统的状态响应是不稳定的；但是在1 s后，具有良好的稳定性。闭环系统的控制输入如图2所示，扰动输出如图3所示。

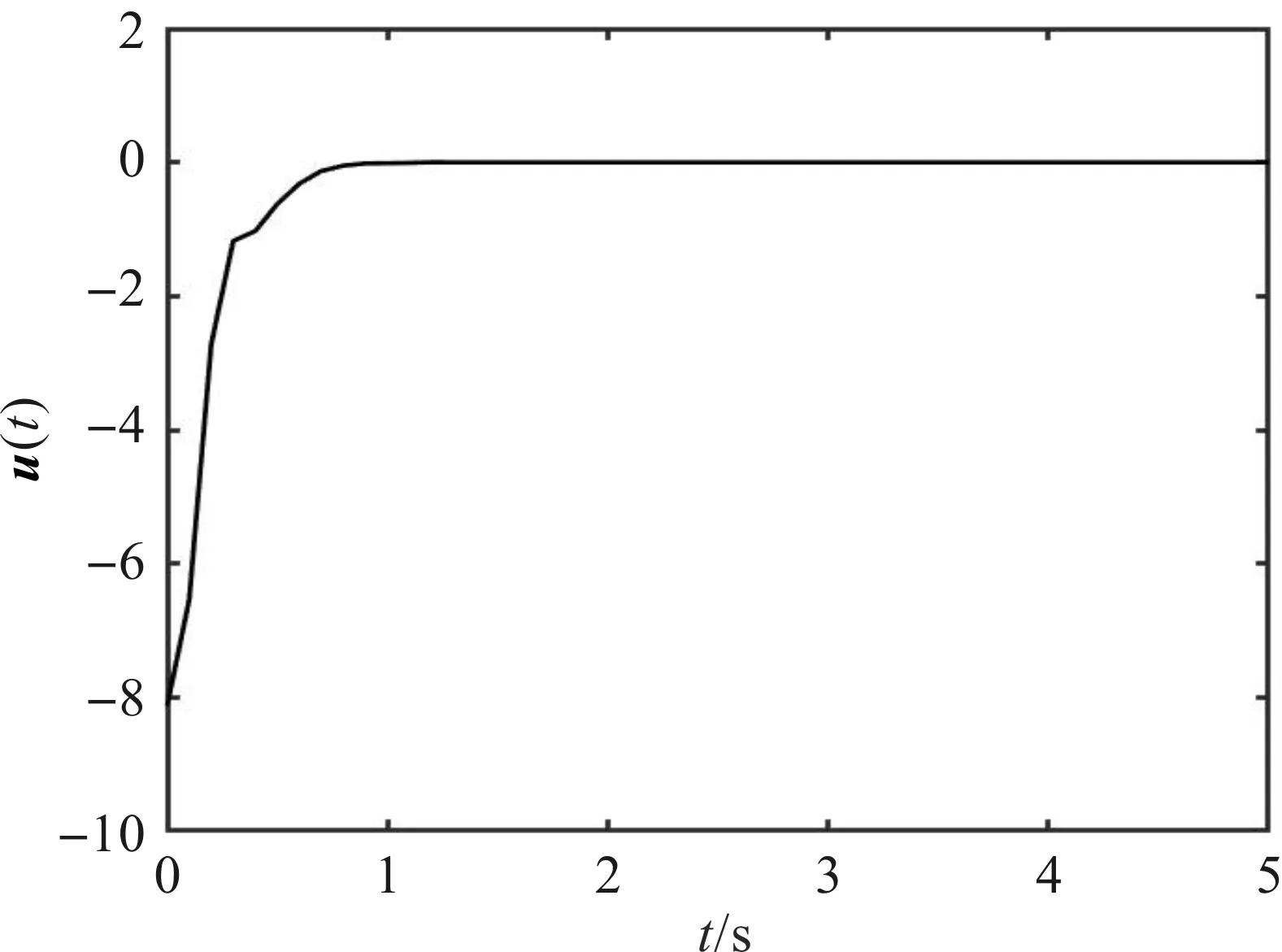
图2 闭环系统的控制输入u(t)

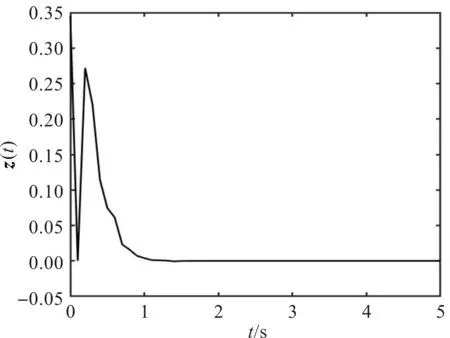
图3 闭环系统的控制输出z(t)

从图2可以看出，0～1 s时，闭环系统的控制输入的变化速度非常快，说明不稳定；1 s之后，控制输入平缓且稳定。从图3可以看出，H∞性能指标γ=2.50时，0～1 s时，闭环系统的控制输出具有较多的突变，极其不稳定；1 s之后，控制输出趋于稳定。

4 结束语

本文研究一类连续时间上的非齐次Markovian跳变随机奇异区间二型模糊系统满足H∞性能指标下的稳定性分析问题。考虑系统结构不确定、带有外部干扰等因素，根据伊藤公式无穷小算子的定义，并结合不等式放缩方法得到系统随机稳定的充分条件，在满足鲁棒性能指标的条件下，设计了满足H∞性能指标的状态反馈控制器。但是，本文未考虑事件触发下的控制器设计问题，后续将针对基于动态事件触发机制下的不确定非齐次Markovian跳变随机奇异区间二型模糊系统展开研究。