基于粗糙集的大学生创新创业团队评价模型的研究
2022-04-06江伟,程奉
江 伟,程 奉
(1.湖北科技学院 计算机科学与技术学院,湖北 咸宁 437100;2.湖北科技学院 外国语学院,湖北 咸宁 437005)
在当前高速发展的时代,我国鼓励大众创业,万众创新[1]。高校对创新、创业的大学生在硬件设备、场地空间、创业指导、资金支持、学分奖励等方面,给予全方位的支持。在政策的推动激励下、媒体的宣传引导下,大学生的创业热情也在持续升温。
创业孵化园是集专业实践实训、就业指导、创业扶持等为一体的创业模式[2]。为更好地规范、引导、推动大学生的创新创业,高校纷纷成立了创业孵化器(园)。大学生要想创业,组建团队并申请入驻孵化器是其成功的必要环节。因此,对申请入驻的团队进行评价,并挑选优秀的团队进行孵化,是高校校园孵化器的重要工作。
当前对大学生创新创业团队评价模型的研究,主要从二个方面展开:一方面是对创新创业团队评价指标的研究。这类研究,主要集中在对创新创业能力的评价指标方面[3-4],例如,创新思维、创新意识、开拓精神、沟通与合作能力、创业能力、企业家素养、学科竞赛能力、科研能力、创业比赛能力等。对创业实践的研究较少,特别是对项目的先进性以及项目开展情况的评价指标,几乎没有。另一方面是对数据的分析与评价模型的研究。这类研究有:基于模糊集理论的FCE法、MFCE法评价模型,基于信息学的熵权法、熵值法评价模型,基于粗糙集理论的评价模型,以及多学科整合的网络层次分析法(ANP)评价模型等[5-8]。
上述文献在构建大学生创新创业团队评价指标体系时,对于团队已开展的项目先进性及其开展情况,还未见有文献将其纳入评价指标体系。另一方面,比较多个文献,仅有文献[8]将Rough集理论运用在大学生创新创业团队评价模型中。因此,基于Rough集理论的评价模型也有较大的研究空间。
本文在二个方面开展研究工作:一方面,完善大学生创新创业团队评价指标体系;另一方面,利用Rough集理论,构建指标客观权重的约简算法,再将各指标的客观权重与考虑经验值的主观权重,按比例结合起来得到一个评价模型,并按此模型计算出文中实例的评价结果。
一、Rough集的相关知识
Rough集由波兰数学家Pawlak于1982年提出,它是一种数据分析理论,它最大的特点是不依赖先验知识,就可以处理不确定、不精确信息,只需数据本身就可以提取出数据之间的内在规则。现在有一些学者将粗糙集理论引入决策科学,利用粗糙集的这一特性,客观地确定各种指标的权重[9]。
1.Rough集的基本概念

定义2[10]令P⊂A,P是属性集A的子集,则ind(P)是属性集P所有属性关系的交集,也称为不可区分关系:
ind(P)={(x,y)∈U×U|∀a∈P,f(x,a)=f(y,a)}
(1)
U/ind(P)(简记为U/P)表示不可区分关系在U上的划分,有U/P={P1,P2,…,Pk}。其中任意元素Pi有:U=U{Pi∈U/P|Pi⊂U}。
特别的对于条件属性集C,有U/ind(C)(简记为U/C)。而U/(C-Ci)表示去掉条件属性Ci后的不可区分关系在U上的划分。
定义3[10]S=(U,R)是一个知识决策系统,令{X1,X2,…,Xm}为一簇集合,对于每一个子集Xi⊂U,设R是U上的等价关系,则有:
R(X)=∪{Y∈U/R|Y⊆X}
(2)
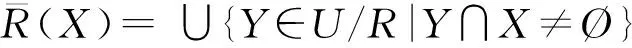
(3)

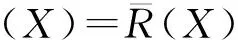
定义4[10]S=(U,C,D,V,f)是一个知识决策系统,令{X1,X2,…,Xm}为一簇集合,Xi⊂U,且U/C={X1,X2,…,Xm},为条件属性集C对论域U的一个划分。U/D={D1,D2,…,Dn}表示决策属性集D对论域U的一个划分,则条件属性集C在论域U关于决策属性D的正域表示为:

(4)
其中CXi=U{Y∈U/C|Y⊆Xi},CXi实质是条件属性集C对U/D={D1,D2,…,Dm}的再划分。
2.基于Rough集的属性指标权重
定义5[10]S=U,C,D,V,f)是一个知识决策系统,如果ind(C)⊆ind)D),则称决策属性D依赖于条件属性C,γC(D)为其依赖程度,有:
κ=γC(D)=|POSC(D)|/|U|
(5)
其中|…|为集合基数运算符号。
σCD(Ci)=γC(D)-γC-Ci(D)
(6)
为条件属性Ci的重要程度。
则条件属性Ci所占权重比例的计算公式为:
(7)
二、大学生创业团队评价指标
本文参照当前大学生创新创业能力的评价指标体系[3-8],结合地方高校对应用型人才培养目标的要求,提出了较为全面地考虑主客观要素的大学生创业团队评价指标体系。在本文的指标体系中,创新性地增加了项目先进性和项目实施二个评价指标。见表1。
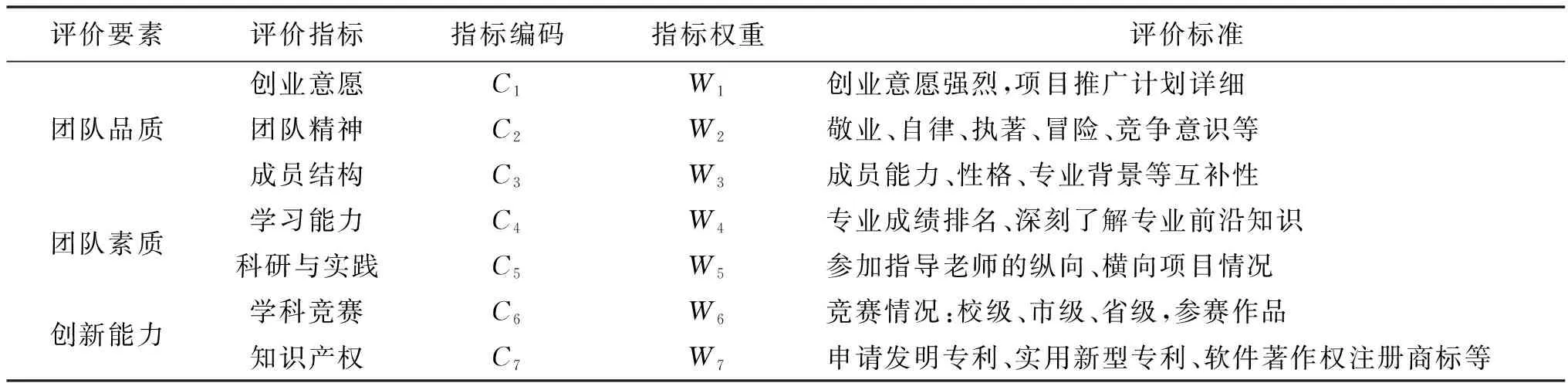
表1 校园孵化器入驻团队评价指标
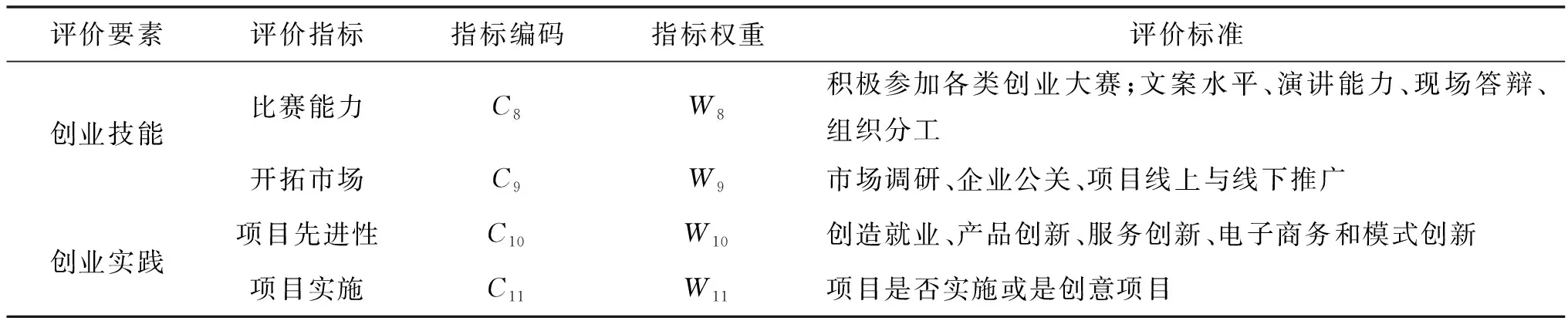
续表1 校园孵化器入驻团队评价指标
三、基于Rough集的大学生创业团队评价模型及实例验证
下面以某高校校园孵化器遴选入驻大学生创业团队为例,依据表1中的指标,给出基于Rough集的大学生创业团队评价模型。表2 中,A1、A2、A3……A18是某高校申请入驻校园孵化器的创业团队编号。
(1)构建论域U和属性集合C
本例中论域U={A1,A2,A3,…,A18}。对于每个Ai构建条件属性集{Ci-1,Ci-2,C1-3,…,Ci-11}:专家参照指标对材料进行评分。同时对数据进行离散化算处理,如(5,90以上;4,80—89; 3,70—79;2,60—69;1,50—59;0,50以下 )。表中科研与实践、学科竞赛、知识产权、比赛能力等指标的评分则是根据团队的实际数据折算后的结果,例如1个省级奖牌等于3个校级奖牌,具体折算方案不在本文中赘述。结合前面的得分,再由审核组,对各个申请入驻团队是否入驻孵化器,给于通过-3、暂缓-2、否决-1的意见,从而构建决策属性集{D1,D2,…,D18}。最后形成一张二维知识表达评价决策表。数据见表2。
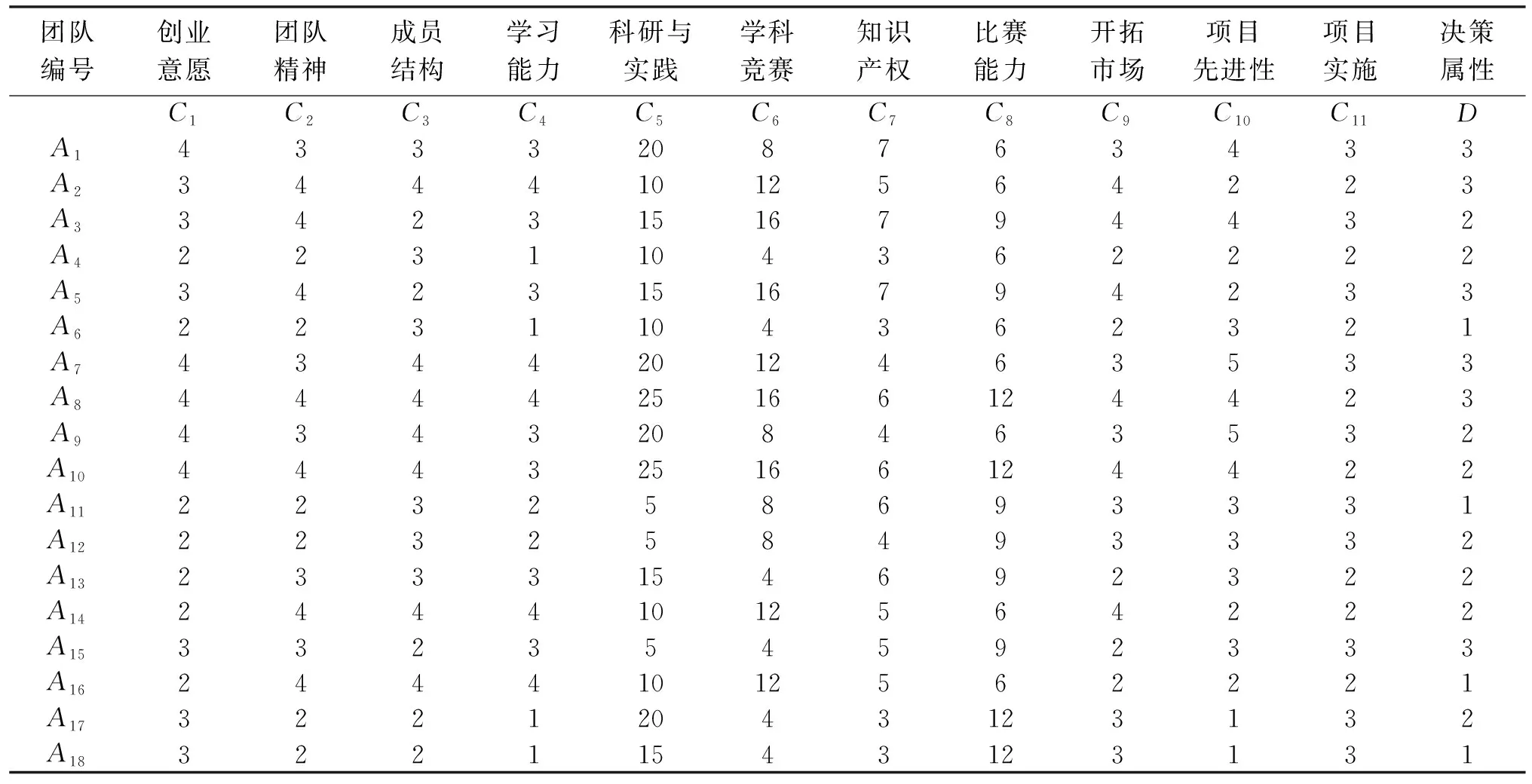
表2 创业团队二维知识表达评价决策表
(2)构建基于条件属性和决策属性的论域等价类。
为了简洁,将U={A1,A2,A3,…,A18}改写成U={1,2,3,…,18}。
U/C1={{1,7,8,9,10},{2,3,5,15,17,18},{4,6,11,12,13,14,16}}
U/C2={2,3,5,8,10,14,16},{1,7,9,13,15},{4,6,11,12,17,18}}
U/C3={{2,7,8,9,10,14,16},{1,4,6,11,12,13,},{3,5,15,17,18}}
U/C4={{2,7,8,9,14,16},{1,3,5,10,13,15},{11.12},{4,6,17,18}}
U/C5={{8,10},{1,7,9,17},{3,5,13,18},{2,4,6,14,16},{11,12,15}}
U/C6={{3,5,8,10},{2,7,14,16},{1,9,11,12},{4,6,13,15,17,18}}
U/C7={{1,3,5},{8,10,11,13},{2,14,15,16 },{7,9,12},{ 4,6,17,18}}
U/C8={{8,10,17,18},{3,5,11,12,13,15},{1,2,4,6,7,9,14,16}}
U/C9={{2,3,5,8,10,14},{1,7,9,11,12,17,18},{4,6,13,15,16}}
U/C10={{7,9},{1,3,8,10},{6,11,12,13,15},{2,4,5,14,16},{17,18}}
U/C11={{1,3,5,7,9,11,12,15,17,18},{2,4,6,8,10,13,14,16}}
U/C={{1},{2},{3},{4},{5},{6},{7},{8},{9},{10},{11},{12},{13},{14},{15},{16},{17},{18}}
U/D={{1,2,5,7,8,15},{3,4,9,10,12,13,14,17},{6,11,16,18}}
(3)计算决策属性集对于条件属性集的依赖程度
POSC(D)={1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18}
(4)构建约简条件属性C-Ci基于论域U的等价划分
U/(C-C1) = {{1},{2,14},{3},{4},{5},{6},{7},{8},{9},{10},{11},{12},{13},{15},{16},{17},{18}}
U/(C-C2) = {{1},{2},{3},{4},{5},{6},{7},{8,},{9},{10},{11},{12},{13},{14},{15},{16},{17},{18}}}
U/(C-C3) = {{1},{2},{3},{4},{5},{6},{7},{8,},{9},{10},{11},{12},{13},{14},{15},{16},{17},{18}}
U/(C-C4) = {{1},{2},{3},{4},{5},{6},{7},{8,10},{9},{11},{12},{13},{14},{15},{16},{17},{18}}
U/(C-C5) = {{1},{2},{3},{4},{5},{6},{7},{8,},{9},{10},{11},{12},{13},{14},{15},{16},{17,18}}
U/(C-C6) = {{1},{2},{3},{4},{5},{6},{7,9},{8,},{10},{11},{12},{13},{14},{15},{16},{17},{18}}
U/(C-C7) = {{1},{2},{3},{4},{5},{6},{7},{8,},{9},{10},{11,12},{13},{14},{15},{16},{17},{18}}
U/(C-C8) = {{1},{2},{3},{4},{5},{6},{7},{8,},{9},{10},{11},{12},{13},{14},{15},{16},{17},{18}}
U/(C-C9) = {{1},{2},{3},{4},{5},{6},{7},{8,},{9},{10},{11},{12},{13},{14,16},{15},{17},{18}}
U/(C-C10) = {{1},{2},{3,5},{4,6},{7},{8,},{9},{10},{11},{12},{13},{14},{15},{16},{17},{18}}
U/(C-C11) = {{1},{2},{3},{4},{5},{6},{7},{8,},{9},{10},{11},{12},{13},{14},{15},{16},{17},{18}}
(5)计算条件属性中Ci的重要程度
1)POSC-C1(D)={1,3,4,5,6,7,8,9,10,11,12,13,15,16,17,18}
POSC-C2(D)={1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18}
POSC-C10(D){1,2,7,8,9,10,11,12,13,14,15,16,17,18}
3)同理可确定其余指标的重要程度:
σCD(C3)=0,σCD(C4)=0.11,σCD(C5)=0.11,σCD(C6)=0.11,σCD(C7)=0.11,σCD(C8)=0,σCD(C9)=0.11,σCD(C11)=0。
由各个σCD(Ci)数据可知,条件属性中Ci的重要程度排序为:
C10>C1=C4=C5=C6=C9>C2=C3=C8=C11=0,并且C2、C3、C8、C11等条件属性对于决策属性D来说是不重要,也是不必要的。
4)计算条件属性Ci的客观权重
根据公式(6)可得C10的权重,ω10=0.25,C1,C4,C5,C6,C7,C9对应的权重ω1,ω4,ω5,ω6,ω7,ω9等为0.125。C2,C3,C8,C11对应的权重ω2,ω3,ω8,ω11为0。
在上述例子中,我们看到,如果评价的对象在某个属性指标上,都取得一样或相近的数据,那么该属性指标对于决策结果的重要程度就会为零或者很小。例如,上例中,C2、C3、C8、C11等属性指标重要程度就为0。这是因为在这18个创业团队中,他们在C2、C3、C8、C11评价指标上取得的成绩是相近的,所以这些指标就会在这次评价过程中,被降低权重,甚至给予0权重。这既是粗糙集属性约简算法的优点,也是它的缺点。优点是:在基于粗糙集的指标权重模型构建完成后,根据每次参评对象所取得的成绩,粗糙集属性约简算法可以动态地自适应调整各个指标的权重。缺点是:粗糙集属性约简算法很容易将一些指标的重要性给忽略,给出明显违反直觉的结论。上例中,指标C8-比赛能力,作为大学生创新创业团队来说是一项重要的技能,赋给权重值不应该为0。这和我们的直觉不相符。因此,有必要对这一问题开展研究。
(6)确定条件属性指标的综合权重
在多属性指标模糊综合评价中,对于指标权重的确定有三类方法:主观赋权法、客观赋权法和主客观组合赋权法。客观赋权法的缺点是忽视了决策者的主观知识与经验等主观偏好信息,有时会出现权重系数不合理的现象[11]。客观赋权法主要包括:熵权法[12]、DEA 法[13]、主成分分析法[14]、离差最大化法[15]、均方差法[16]和基尼系数赋权[17]等。主观赋权法的缺点是受到专家的心理因素和经验知识等的局限,仅仅根据专家的某一次判断而给定权重有时不可靠[18]。主观赋权法主要包括:环比评分法、Fuzzy子集法、二项系数法、专家调查法、属性重要性排序法、判断矩阵法、比较矩阵法和点估计值法等[9]。因此,李刚在文[19]中指出:很多时候不能单纯只考虑指标本身的重要性(主观权重),还应该考虑指标的数据信息(客观权重)。而主客观组合赋权法的出现解决了上述存在的问题[18]。目前主客观组合赋权方法有:客观修正主观、级差最大化、线性加法合成、乘法合成等组合赋权法[19]。
在多数参考文献中,如文[20]、[21],将专家团队的经验知识当作主观权重的首选。这些权重赋权方法实质上还是从管理者视角看问题,存在一定的片面性。黄昱方在文[7]中提出,创业者是创业过程中最为主动、最活跃、最重要的因素,他们往往具有良好的技术背景和创新意识。一名成功的创业者更能深刻了解创业者的所应具备的要素。因此,本文将创业团队的需求和认知经验也纳入指标权重的构建中。表3中各个条件属性指标下的主观权重,分别由专家权重和创业代表权重组成。
综上所述,本文将由Rough集约简算法确定的客观权重与主观权重组合一起,构建一个主客观线性组合的组合赋权评价方法。计算公式如下:
Wi=(Ci)=αλi+βγi+(1-α-β)ωi
(7)
其中,λi为主观权重中的专家权重。γi为主观权重中的创业代表权重,ωi为Rough集的约简算法确定的客观权重;α,β和1-α-β分别为λi,γi和ωi的权重占比,是对主观认知和客观数据认知的深刻程度。α和β越大说明决策者认为评委主观认知深刻,能够给出准确的评价,而1-α-β越大说明决策者认为评委主观认知不足,需要更多依赖于客观数据的分析。各个指标对应的综合权重见表3。
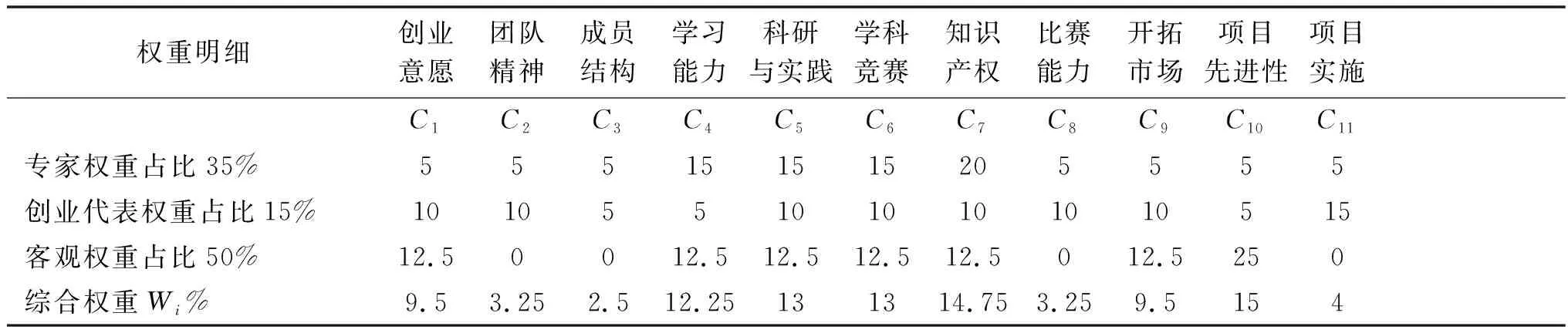
表3 各项指标的综合权重(百分制)
(7)根据综合权重计算最终评价结果
1)对数据进行标准化处理
在多属性指标的决策过程中,由于各个属性指标的评价单位的量纲不一样,会造成错误的评价结果。例如,如果某个指标的数量级较大,虽然其指标的权重很小,也会对结果造成很大的偏差。本文选择极差化方法。[22]公式如下:
(8)
其中, min(xj)为指标k的最小值,max(xj)为指标j的最大值。该方法的特点是:标准化后指标最小值为0,最大值为1,但是对于指标值恒定的情况不适用。
第一步,由表2构建创业团队知识表达二维矩阵:
第二步,利用公式(8)对矩阵A中数据进行标准化。得到矩阵B。B矩阵的具体二维数据见表4。
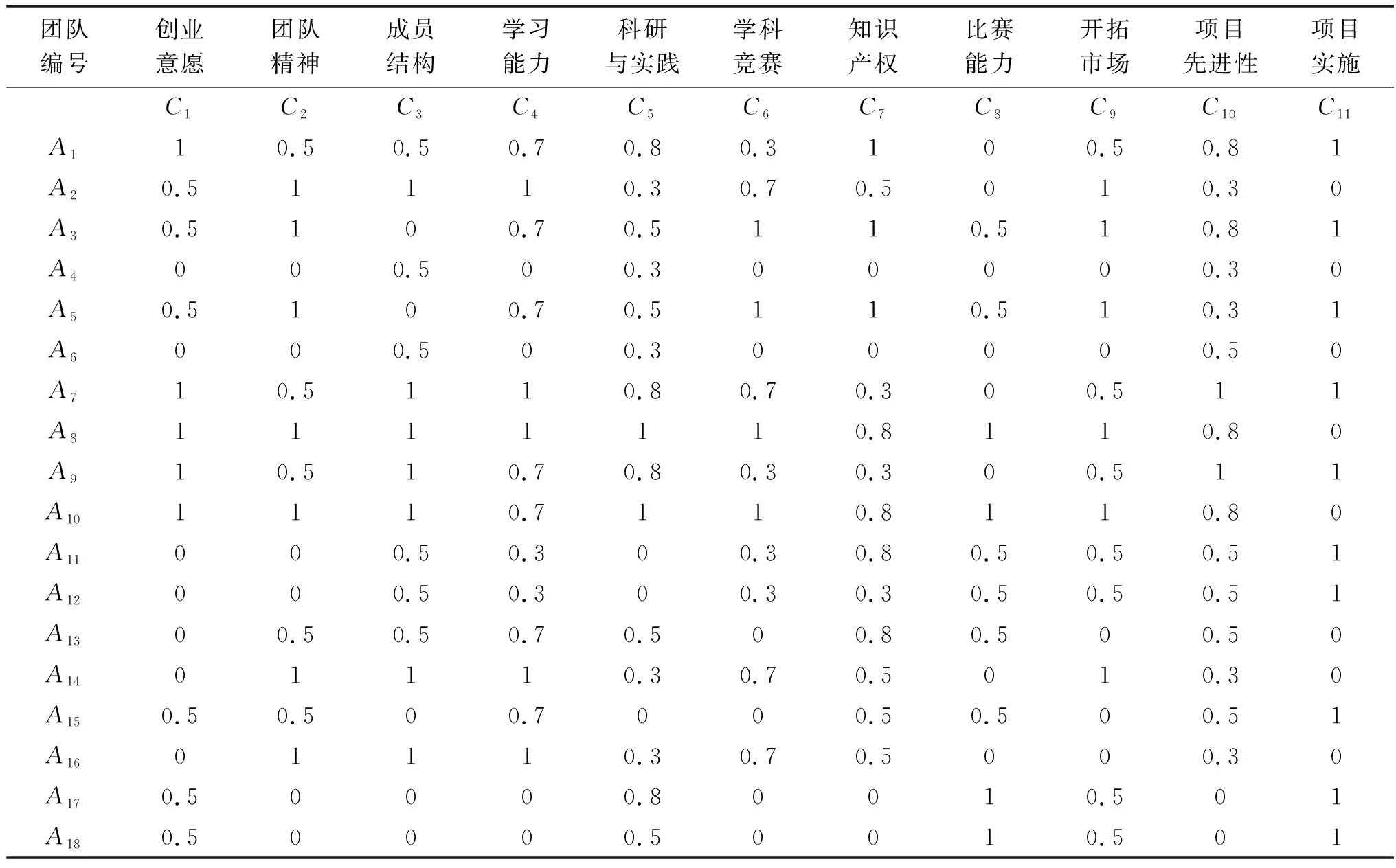
表4 创业团队条件属性二维知识数据标准化表
2)计算评价结果
由表3构建综合权重矩阵:
W=[W1,W2,…,W11]=[0.095,0.0325,…,0.04]
则最终评价结果为:
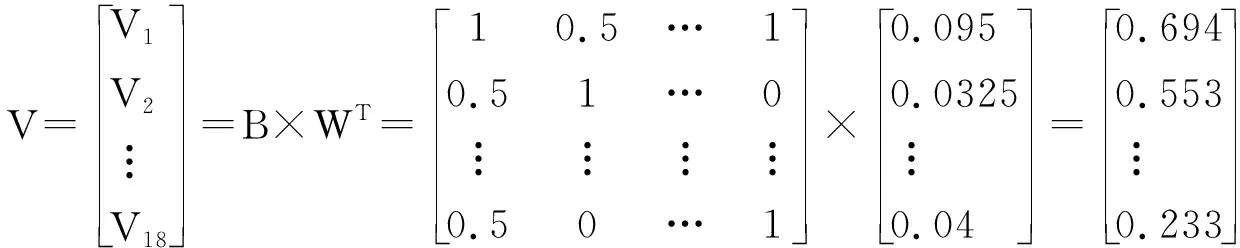

表5 各申报团队评价结果
根据表5,申报团队的排序:A8,A10,A3,A7,A1,A5,A9,A2,A14,A16,A11,A13,A15,A12,A17,A18,A6,A4。
根据上述评价结果,管理层根据排序可以灵活地选择入驻团队、观察团队和否决团队。
四、结论
本文通过集体座谈、问卷调查和文献分析等手段,凝练出校园孵化器遴选大学生创新创业团队的评价指标体系。该指标体系包括团队品质、团队素质、创新能力、创业技能、创业实践等5个要素11个评估点。并给出一套基于Rough集理论约简算法的主客观组合赋权的决策模型。通过实例验证,该模型具有如下特点:
(1) 模型中指标的客观权重是基于Rough集理论的约简算法得出,能够体现数据之间的规律,也是基于数据的约简规则表达,具有非常好的数据科学性。
(2) 对于模型中指标的主观权重,本文首次基于创业团队的视角,充分考虑了被评价对象的需求和认知经验,并与专家经验一起构建主观权重,具有一定创新性。
(3) 在构建指标体系中,首次在创业实践要素中考虑了项目先进性和开展情况。这样,会遴选出兼具社会价值与经济价值、新颖、先进的项目,也将为当前火热的“互联网+” 大学生创新创业大赛提供更多的资源。
