带输入噪声的高斯过程扩展目标跟踪算法

任 磊，郭云飞

(杭州电子科技大学自动化学院，杭州 310018)

0 引 言

随着高分辨传感器技术的飞速发展，扩展目标跟踪(Extended Target Tracking，ETT)技术在边海防监控、海事探测、无人驾驶等军事与民用领域应用日益广泛。与传统点目标跟踪技术相比，ETT框架下的目标回波占据高分辨传感器的多个分辨单元，每帧产生多个随机散射点，利用这些散射点产生的含噪测量，ETT不仅要准确估计目标的运动状态(位置、速度等)，还要估计目标的轮廓状态(大小、形状等)[1]。早期的ETT算法包括序贯蒙特卡洛法、随机矩阵法(Random Matrix, RM)[2]、随机超曲面模型法(Random Hyper-surface Model, RHM)[3]等。2015年，Wahlstrom等[4]提出一种基于高斯过程(Gaussian Process, GP)的ETT算法。ETT算法运用GP强大的学习能力，对理想环境下星凸形状扩展目标的轮廓函数进行在线学习，实现了非椭圆形状扩展目标的递推估计[5]。基于高斯过程的扩展目标跟踪(Gaussian Process Extended Target Tracking，GP-ETT)算法在贝叶斯框架下能准确估计星凸形状目标的轮廓及运动特征，在高分辨传感器探测与监控领域得到广泛应用。进一步地，文献[6-7]提出基于GP的概率数据关联(Probabilistic Data Association, PDA) 技术，解决了杂波环境下星凸形状扩展目标跟踪问题，并推广到多机动扩展目标跟踪。上述GP-ETT技术中，通常忽略了目标局部坐标系中的角度测量估计的不确定性[8]。当测量误差较大或目标运动状态估计误差较大时，破坏了GP的预测方差，影响了ETT的跟踪性能[9]。文献[8,10-11]从不同角度分析了带输入噪声时GP的均值和协方差，并将其用于非线性滤波和地球遥感等领域。文献[12]使用泰勒级数法修正了GP-ETT的模型输出，但未深入分析输入不确定性对GP预测协方差及性能界的影响。为此，本文提出理想环境下带输入噪声的GP-ETT算法，通过推导得到预测协方差及状态估计的后验克拉美罗下界(Posterior Cramér-Rao Lower Bound, PCRLB)[13]。

1 高斯过程

1.1 标准高斯过程

GP是一种非参数的随机过程，本质上是多维高斯分布的扩展。由于GP能够利用训练数据对一个未知函数进行建模和学习，广泛用于信号处理、机器学习等领域[5]。假设待拟合函数如下：

y=f(x)+ε

(1)

式中，x∈Rd为输入量，y∈R1为输出量，f(·)为未知函数，观测噪声ε服从如下高斯分布：

ε～N(0,σ2)

(2)

给定包含n个训练数据对的集合D=[X,y]，其中X=[x1,x2,…,xn]，y=[y1,y2,…,yn]分别为训练输入集与输出集，则未知函数f(·)表示为如下高斯过程：

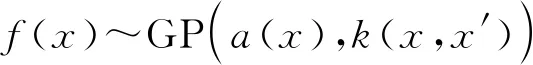
(3)

式中，a(x)和k(x,x′)分别为f(x)的均值函数和协方差核函数，通常，协方差核函数k(x,x′)选择的平方指数(Square Exponential, SE)函数如下：

(4)

式中，σf和l为GP的超参数。在标准高斯过程中，假设测试输入x*为精确已知量。对于测试输入x*，其对应的GP预测值的后验分布为：

(5)

式中，均值μ(x*)及协方差ν(x*)分别为：

(6)

(7)

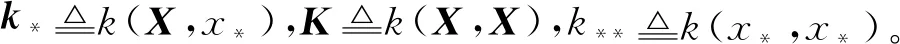
1.2 带输入噪声的高斯过程

在实际应用中，高斯过程的测试输入有时难以准确获取，存在输入不确定性。该不确定性可以用输入噪声进行建模，假设该噪声服从如下高斯分布：

(8)

式中，m(x*)与Σ*分别为测试输入x*的估计均值与方差。式(8)中，含有输入噪声的测试输入x*对应的GP概率分布为：

(9)

大多数情况下，式(9)难以获得解析解，近似求解的思路主要有数值近似法和泰勒级数法(Taylor Series, TS)。数值近似法可采用Sigma采样法(Sigma Sampling, SS)和蒙特卡洛采样法(Monte-Carlo, MC)。本文分别采用Sigma采样法、MC采样法和泰勒级数法近似带噪声的GP的分布，提出3种基于带噪声GP的ETT算法，分别记为GP-TS，GP-SS和GP-MC。

2 基于GP的ETT算法

在传统目标跟踪领域中，通常仅关心目标的运动状态，如位置、速度、航向角等，目标可用一个“点”来描述。当目标距离传感器较近或者传感器分辨率较高时，目标轮廓特征不可忽略，需要描述为“扩展目标”[1]。常用的ETT建模算法包括RM[2]，RHM[3]，GP[4]等。与其它算法相比，GP能够更加准确地估计目标的形状特征。

2.1 GP-ETT的动态模型

(10)

(11)

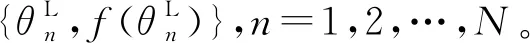
(12)

考虑到GP输入θL的周期性，GP的均值函数及协方差函数建模如下：

(13)

(14)

式中，σf为轮廓径向函数的标准差；σr为均值半径的标准差；l为尺度因子。根据GP性质，式(12)可进一步改写为[4]：

(15)

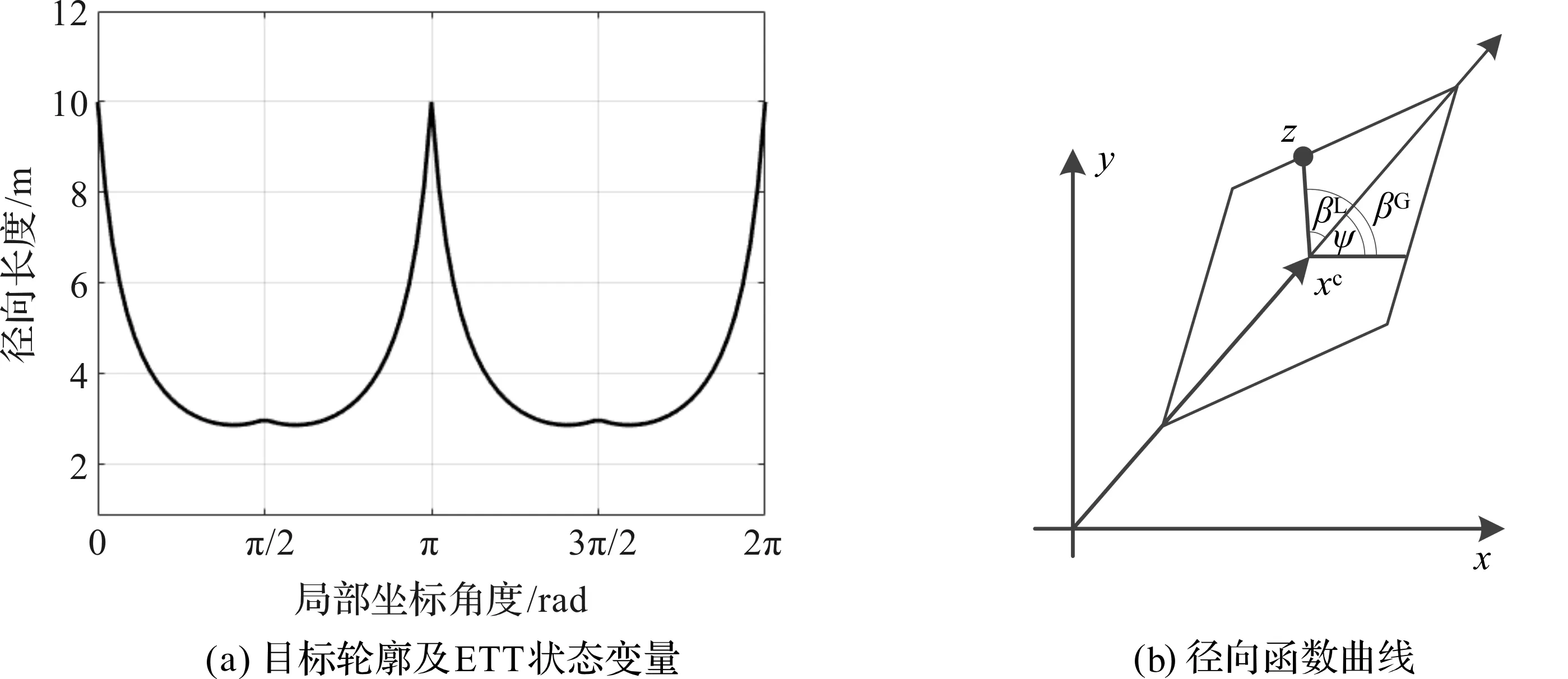
图1 菱形目标的径向函数及其轮廓

GP-ETT的动态模型可写为：

(16)

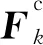
2.2 测量模型

ETT的一个典型特征是一个目标在单帧内包含多个随机散射点，能产生多个测量。这些散射点可能分布在目标轮廓边缘，也可能分布在目标轮廓内部[4]。本文旨在讨论输入噪声对GP-ETT的影响，为了简便计算，假设散射点分布在轮廓边缘。

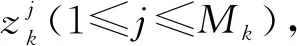
(17)

(18)

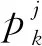
(19)

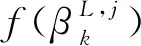
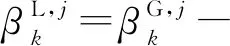
(20)

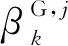
(21)

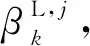
(22)

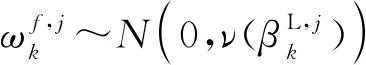
(23)

(24)

3 带输入噪声的GP-ETT算法

3.1 GP的噪声输入方差

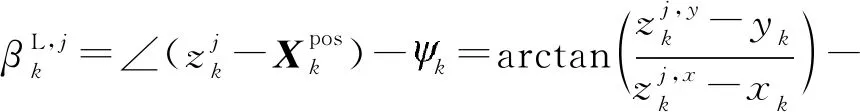
(25)

(26)

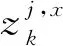
根据式(24)，测量噪声的方差记为Rk。假设测量在各坐标轴拥有相同的不确定度，即令

(27)

(28)

进而得该矩阵的相似对角阵Psim，

(29)

根据随机误差传递公式[14]，GP输入的方差Σβ表示为：

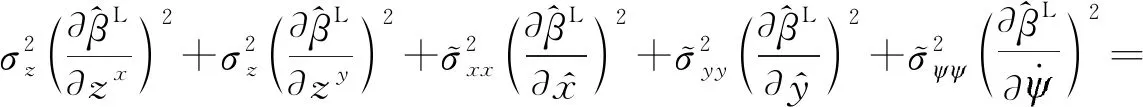
(30)

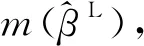
3.2 泰勒级数法

(31)

其相应的均值和协方差为[9]：

(32)

(33)

对标准高斯过程的预测均值函数μ(x*)在x*=m(x*)处进行一阶泰勒展开，可得：

(34)

(35)

同理，对ν(x*)进行一阶泰勒展开，可得：

(36)

忽略其余项，求其均值，可得：

(37)

最后，对μ(x*)进行一阶泰勒展开，可得：

(38)

对其求方差，可得：

(39)

所以，运用泰勒级数法可求得带有噪声输入的高斯过程的预测均值函数和协方差函数，分别为：

(40)

(41)

式中，μ′(m(β))分别为μ(β)关于β的一阶偏导在m(β)处的取值，

(42)

其中，

(43)

将(42)代入式(41)，即可得到GP-ETT中带输入噪声的GP预测均值与预测协方差。

3.3 数值近似法

数值近似法通过采样点对无法获得解析解的积分进行近似求解。常用的数值近似法有Sigma采样法和MC采样法。

则有输入噪声的GP预测均值函数和协方差函数为：

(44)

(45)

(46)

(47)

从式(41)可以看出，增加一个噪声项，增加了GP模型的不确定性，所以，带有噪声的GP模型的协方差大于标准GP模型的协方差。

4 PCRLB

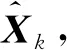
(48)

式中，Jk为Fisher信息矩阵，其递推表达式为：

(49)

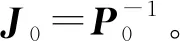
(50)

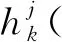
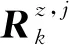
(51)

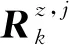
(52)

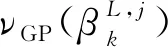
5 仿真实验及分析

通过一个复杂形状的扩展目标进行仿真实验，其目标轮廓及半径函数如图2所示。

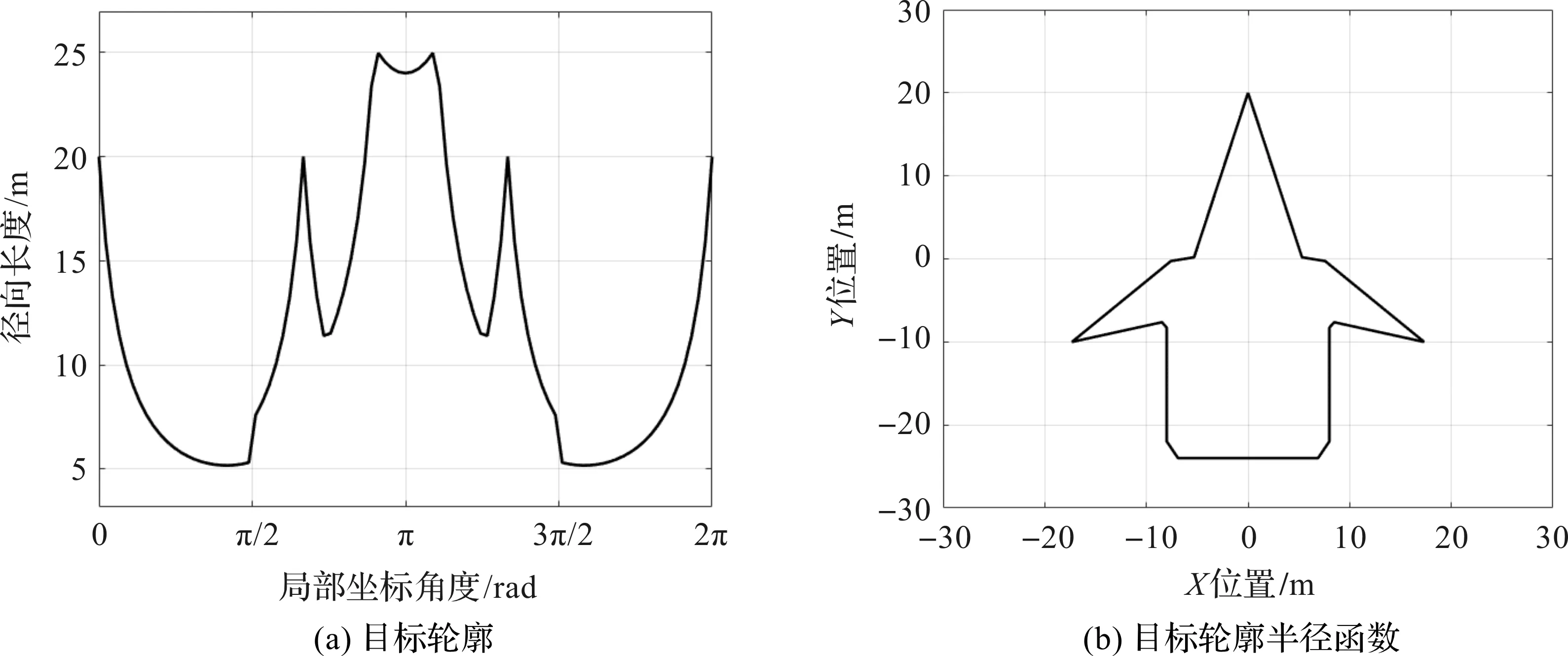
图2 目标轮廓及半径函数

目标作近似匀速直线运动，初始运动状态的均值为X0=[10 m,2 m,10 m,2 m,π/4 rad,0 rad/s]T，协方差为P0=diag{1 m2,0.1 m2/s2,1 m2,0.1 m2/s2,0.1 rad2,0.001 rad2/s2}，目标的轮廓状态初值为半径为1的圆。假设跟踪期间轮廓时不变，轮廓状态转移矩阵为Ff=IN，其中IN表示N维单位矩阵，过程噪声Qf=0。传感器位于坐标原点，测量噪声标准差为σz=1 m，测量时长为100 s。目标散射点的个数服从泊松分布，泊松参数为λt=0.8。高斯过程的超参数为σr=2，σf=2，l=π/18。Monte Carlo仿真次数为100。

使用基于RM和GP的ETT算法进行仿真，跟踪效果如图3所示。

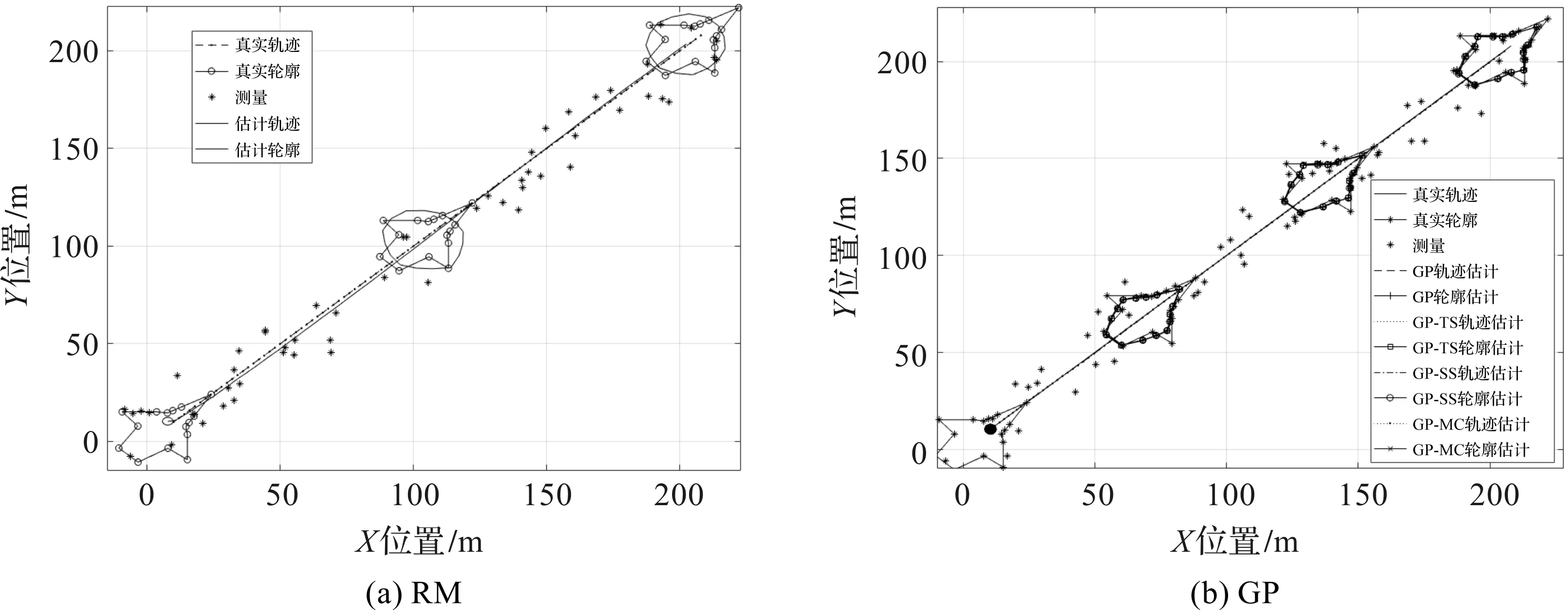
图3 基于RM和GP的ETT算法的跟踪效果

从图3可以看出，在理想环境下，2种算法均能估计目标的运动状态和扩展状态。基于GP模型的ETT算法可以对目标轮廓进行精确估计，而RM模型只能利用椭圆对扩展目标大小进行估计，不能精确估计其形状。

当k=100 s时，分别采用GP, GP-TS, GP-SS, GP-MC算法对目标轮廓进行估计，结果如图4所示，4种算法的轮廓估计误差棒图如图5所示。

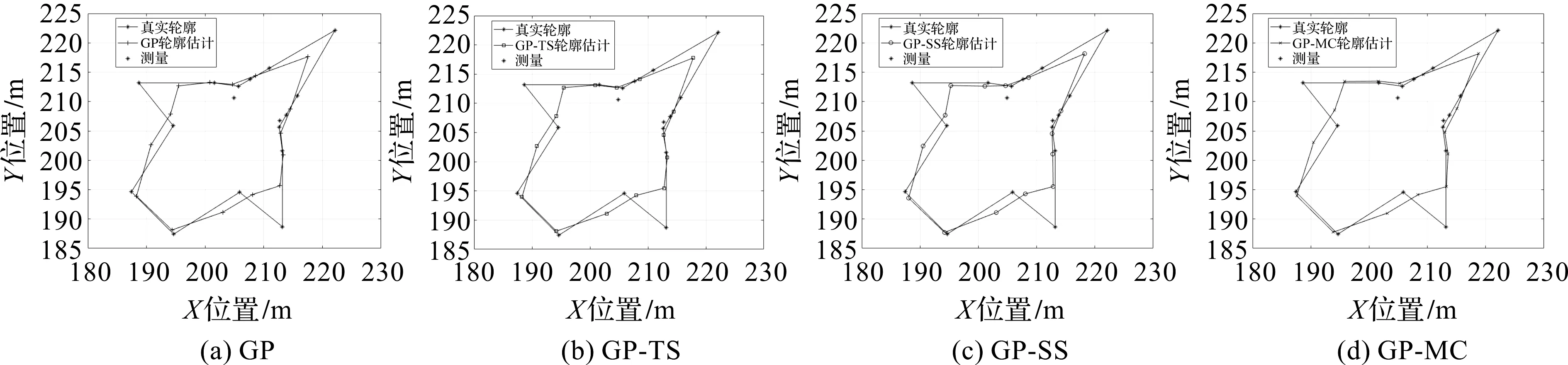
图4 4种GP算法轮廓估计

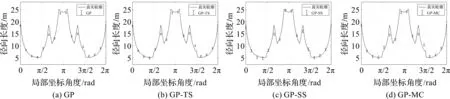
图5 4种算法的轮廓估计误差棒图

从图4可以看出，4种算法都能较好地对目标轮廓进行精确估计。从图5可以看出，本文提出的带输入噪声的3种GP算法的不确定度区间对真值覆盖情况更好，二阶估计更加合理。

选择扩展目标轮廓均方根误差(Root Mean Squared Error, RMSE)、PCRLB与马氏距离(Mahalanobis Distance, MD)等指标来衡量算法的跟踪性能。4种算法的性能指标如表1所示。

表1 4种算法的性能指标

从表1可以看出，4种算法的RMSE比较接近，其中GP-MC最优；带输入噪声的3种GP算法的MD指标更优，得到的PCRLB最保守，并且都获得了最更小的MD。总体看来，相比于标准GP算法，本文提出的带输入噪声的GP算法的估计性能更好。

6 结束语

本文定量分析了输入噪声对GP预测结果的影响，提出3种带输入噪声的GP-ETT算法，并推导理想环境下带输入噪声的GP-ETT的最优理论性能界，得到更加合理的二阶估计和更加保守的PCRLB。本文进行算法模型设计时，假设的环境较为理想，比如无杂波理想环境、目标形状无形变等，但在实际应用环境中，难免会有一些偏差。后续将考虑更多实际因素，进一步优化模型，使其更贴近实际应用。