忆阻Hopfield神经网络的混沌特性研究
2022-04-06王光义
蒋 欣,王光义,周 玮
(杭州电子科技大学现代电路与智能信息研究所,浙江 杭州 310018)
0 引 言
Hopfield神经网络(Hopfield Neural Network, HNN)是一种反馈型神经网络[1],越来越多的证据表明大脑中存在复杂的混沌动力学[2],HNN能较好地模拟大脑中的混沌行为,为理解人类大脑活动和记忆行为提供重要模型。相关研究发现一些复杂的混沌现象[3]。大脑的神经活动可以从混沌状态转为周期状态,混沌状态对应大脑的正常运作状态,周期性状态对应癫痫发作等病理状态[4]。双曲型HNN[5]可简化连接的拓扑结构,出现不同种类吸引子的共存行为[6]。在HNN模型中,将神经元激活梯度作为可调控参数时,可产生共存周期和混沌振荡[7]。三次磁控忆阻器也可实现忆阻HNN,出现准周期、混沌及超混沌现象[8]。Danca等[9]研究简化型三元HNN,通过数值分析和仿真实验发现2个稳定周期吸引子外,还发现隐藏的混沌吸引子和瞬态混沌吸引子。忆阻器具有纳米结构、阻值连续可调和记忆特性[10-13],选择忆阻器作为突触可提高神经网络处理不同问题的灵活性,还可实现神经网络突触的可编程性[14]。随着HNN在科学和工程领域的广泛应用,忆阻器已成为新型神经形态计算的最佳候选器件之一[15]。本文将忆阻器模型引入神经网络,设计一种四元忆阻Hopfield神经网络。
1 四元忆阻Hopfield神经网络数学模型
忆阻器是一个具有记忆性的非线性电阻,其具有纳米结构、低功耗和阻值可调等特性,非常适合模拟神经突触和神经元。忆阻器有荷控(流控)和磁控(压控)两种类型[16],神经元激活函数是单调可微且上下有界的,通常采用双曲正切函数作为神经元的激活函数。本文采用双曲正切型忆阻器来模拟神经元突触,其模型为:
(1)
式中,vm和im分别为忆阻器的输入电压和电流,W(φ)=a-btanh(φ)为磁控忆阻器的忆导,其中,a,b均为正实数,为了便于计算分析,令a=1,b为可调参数。
“突触权重”代表神经元之间的连接强度,本文引入忆阻器来取代第4个神经元的自连接突触权重W44,设计的四元忆阻Hopfield神经网络的拓扑连接如图1所示。
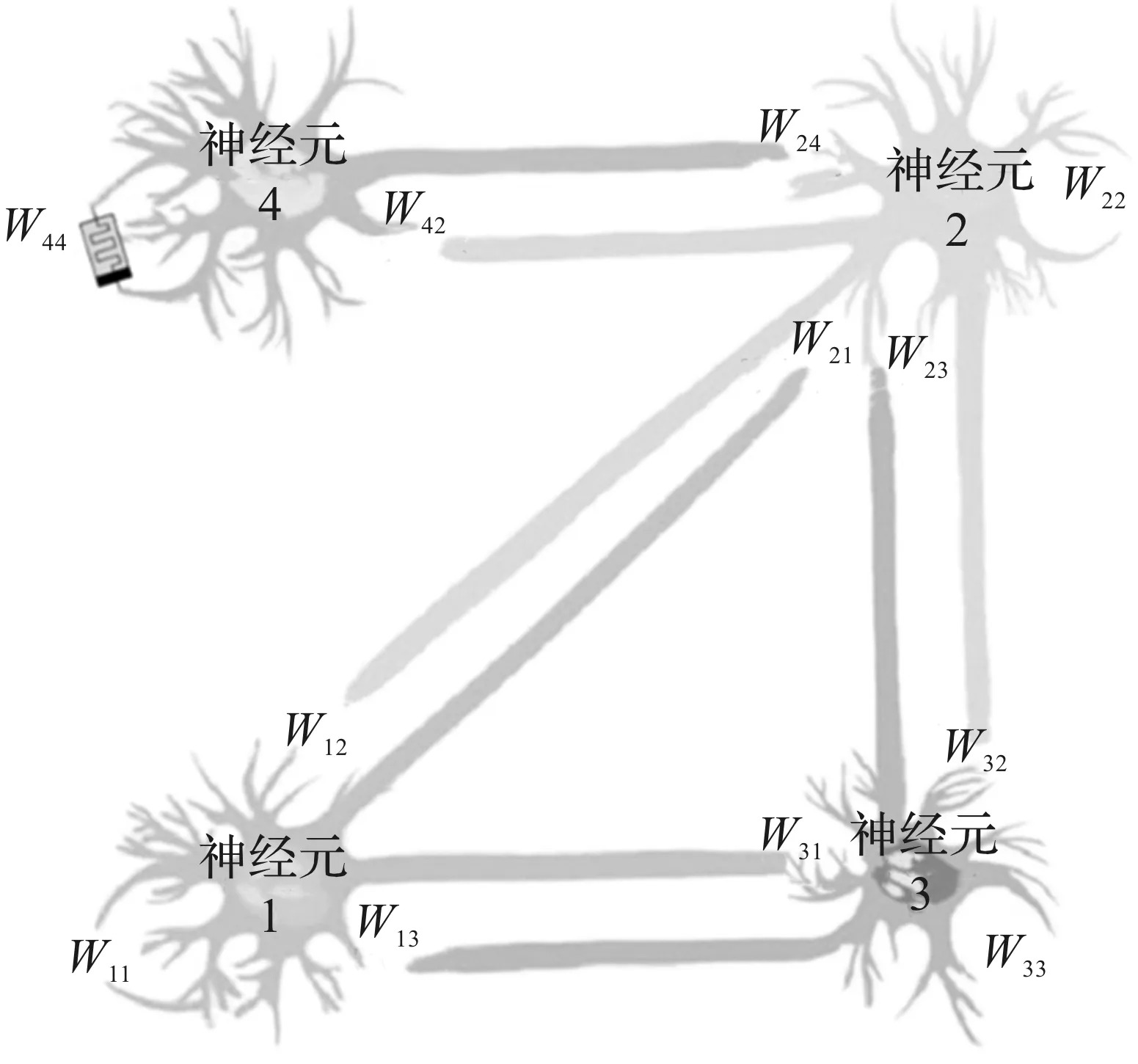
图1 四元忆阻Hopfield神经网络拓扑连接
图1中,W11,W22,W33和W44分别为4个神经元的自连接权重,W12,W21,W13,W31,W23,W32,W24,W42分别为4个神经元的互连接权重。
常用双曲正切函数tanh(xn)(n=1,2,3)作为从第n个神经元电压输入的神经元激活函数,其系数表示2个相邻神经元之间的连接突触权重,Hopfield神经元的电路方程为:
(2)
式中,Ci,Ri和xi为神经元i细胞膜内外的电容、电阻和电压,tanh(xi)为神经元激活函数,Wij为描述神经元i与神经元j之间连接强度的突触权重,W11,W22,W33和W44分别为4个神经元的自连接权重,Ii为偏置电流,通常等于0。
忆阻器的忆导或忆阻随其电流改变的特性与人脑突触极为相似,用忆阻器模拟神经元突触更符合生物学特性。本文通过多次仿真实验,得到如下突触矩阵:
(3)
式中,W24和W42为神经元2和神经元4之间的互连接突触,W′44为系统参数,是一个常数,根据式(3)和图1得到如下忆阻HNN数学模型:
(4)
式中,x,y,z,u,w为神经网络的状态变量,适当的参数使得该神经网络产生混沌现象。选取系统参数W24=3.8,W42=1.0,W′44=-1.5,忆阻器内部参数b=0.3,产生的混沌波形和x-u平面的吸引子相图如图2所示。
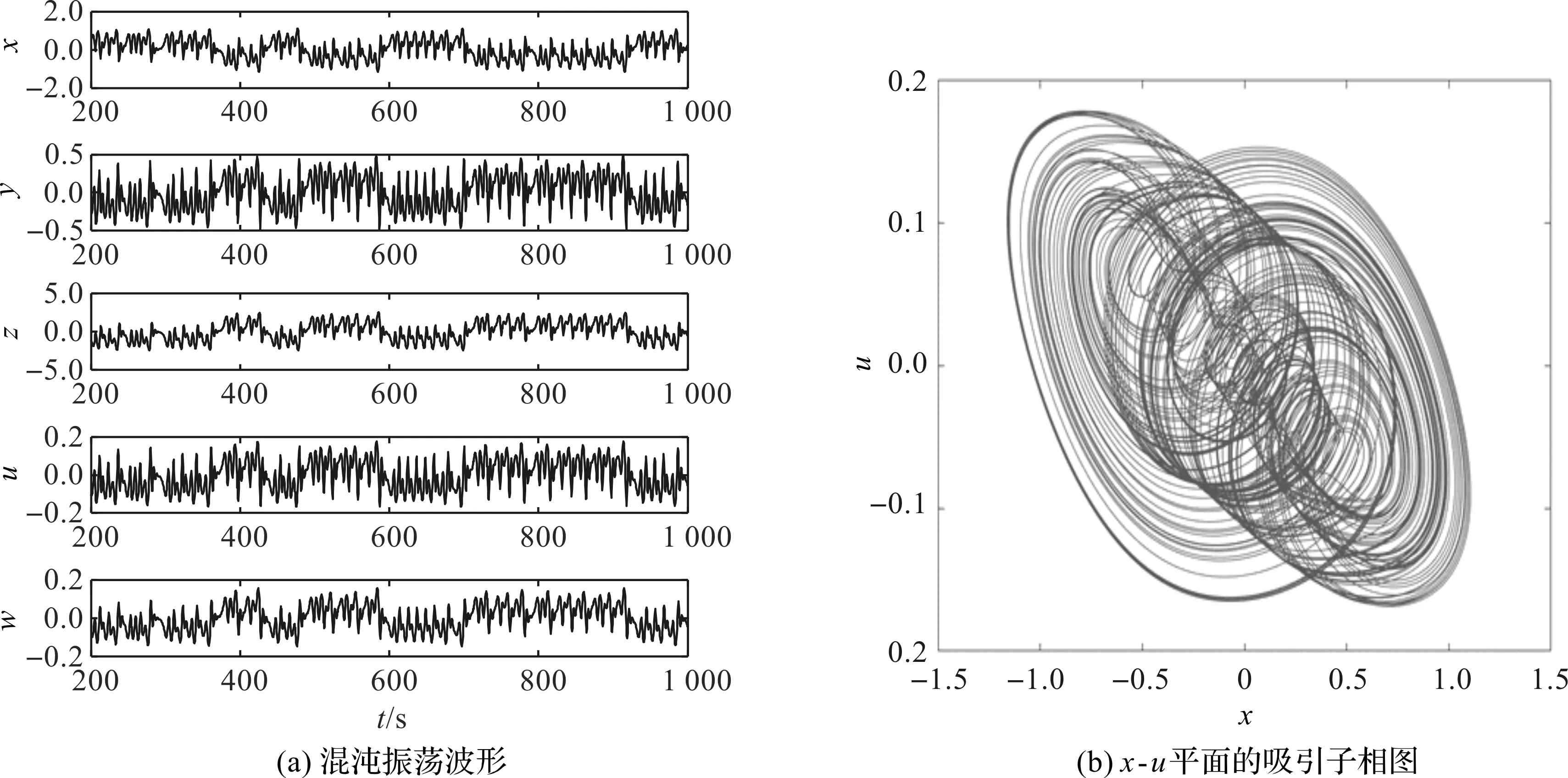
图2 四元忆阻器Hopfield神经网络的混沌特性
从图2可以看出,振荡波形是非周期、伪随机的,神经网络产生了双涡卷混沌吸引子。
2 四元忆阻器Hopfield神经网络的平衡点和稳定性分析
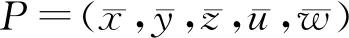
(5)
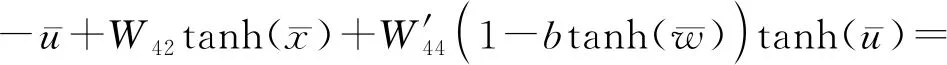
(6)
当忆阻器内部参数b=0.3时,平衡点P0,P1和P2的特征值和稳定性如表1所示,其中i表示复数的虚部单位。

表1 b=0.3时平衡点及其特征值和稳定性
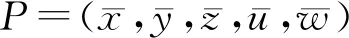
(7)
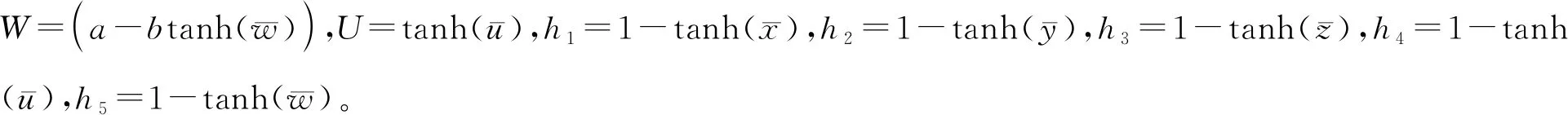
3 关键参数对四元忆阻Hopfield神经网络动力学特性的影响
3.1 忆阻器内部参数b对神经网络动力学的影响
当忆阻器内部参数b在[0,3.0]区间变化时,四元忆阻Hopfield神经网络的分岔图及Lyapunov指数谱如图3所示,为了便于观察,第4条和第5条Lyapunov指数谱未展示,其值恒为更小的负值。
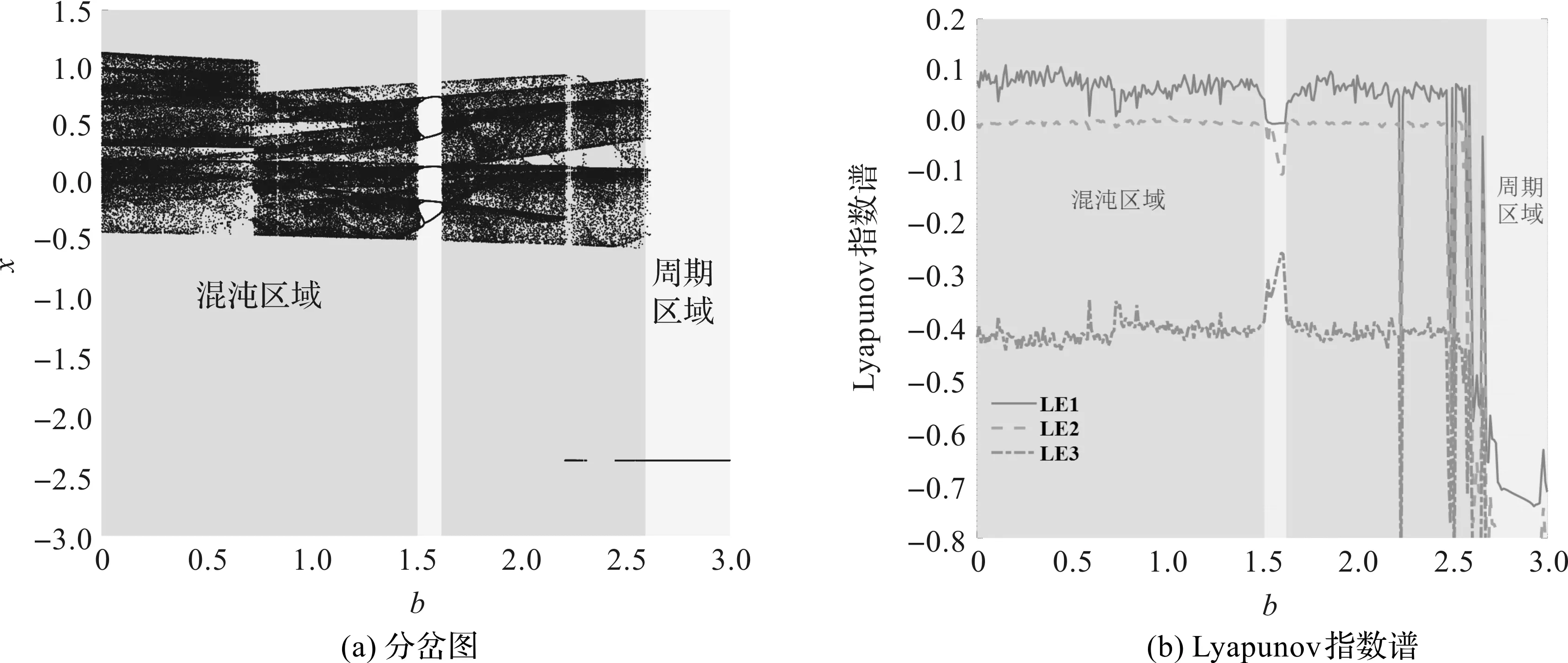
图3 四元忆阻Hopfield神经网络随参数b变化的情况
从图3可以看出,随着忆阻内部参数b的增大,除中间出现的短暂周期窗口外,该神经网络基本处于混沌状态,最终进入稳定状态。
当参数b的取值分别为0.3,0.7,1.6,1.8时,四元忆阻Hopfield神经网络的相图如图4所示。

图4 四元忆阻Hopfield神经网络随参数b变化的相图
从图4可以看出,随着参数b的变化,神经网络产生了2种不同类型的混沌吸引子,即双涡卷和单涡卷混沌吸引子。由图3和图4可知,忆阻参数b的影响较大,随着b的变化,神经网络呈现不同的状态,包括周期吸引子、单涡卷混沌吸引子及双涡卷混沌吸引子。
3.2 串扰参数对神经网络动力学的影响
文献[17]研究表明,神经元突触间存在突触串扰的现象。突触的串扰行为影响神经元之间的连接强度,忆阻参数b的变化控制着神经元4的自连接突触权重,突触串扰引起其他突触权重W24,W42及W′44的变化。本文将W24,W42及W′44定义为神经元的串扰参数,以串扰参数W24为例进行分析。
四元忆阻Hopfield神经网络随串扰参数W24变化的分岔图及指数谱如图5所示。
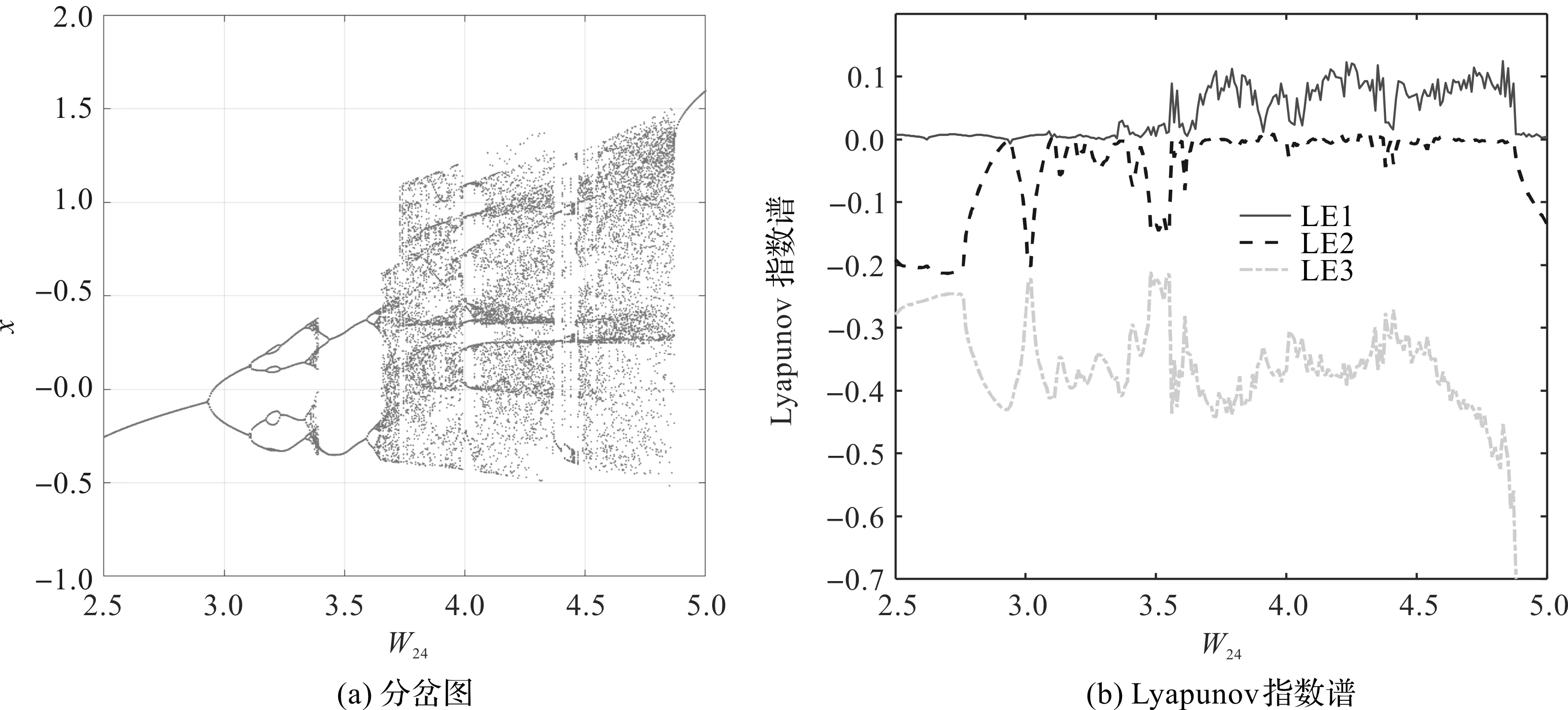
图5 四元忆阻Hopfield神经网络随参数W24变化情况
从图5可以看出,当W24在[2.5,5.0]内变化时,神经网络反复出现倍周期分岔和逆倍周期分岔状态,最后,通过倍周期分岔切换到混沌轨道。W24的取值分别为3.65,3.75,3.80和4.60时,Hopfield神经网络产生了4种不同类型的混沌吸引子相图如图6所示。
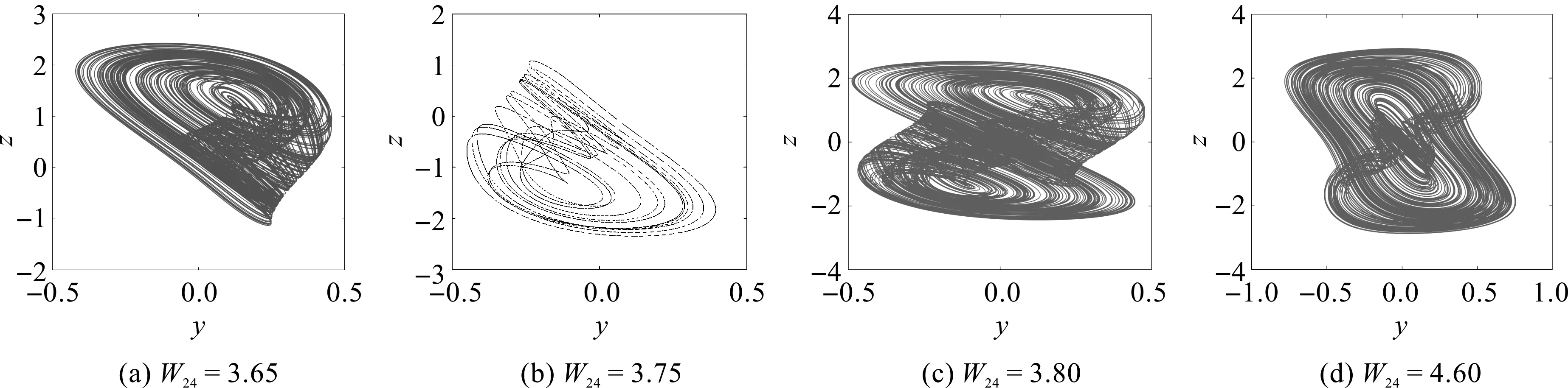
图6 四元忆阻Hopfield神经网络随参数W24变化的相图
从图6可以看出,随着W24的变化,神经网络呈现复杂的混沌状态,包括不同类型的单涡卷混沌吸引子和双涡卷混沌吸引子,说明串扰参数W24对四元忆阻神经网络产生了较大的影响。
4 仿真实验与分析
四元忆阻Hopfield神经网络的主电路如图7(a)所示,参数W′44=-1.5,W42=1.0,b=0.1,取RC的时间常数为1 ms,即R=10 kΩ,C=1 μF,串扰参数W24的值由可变电阻R24控制,电路中其它元件参数分别根据Rij=R/Wij计算。图7(b)为忆阻突触等效电路,其中各元件参数为:R54=R/W54=10.00 kΩ,Ra=R/(a×W′44)=6.67 kΩ,Rb=gR/(b×W′44)=66.67 kΩ。
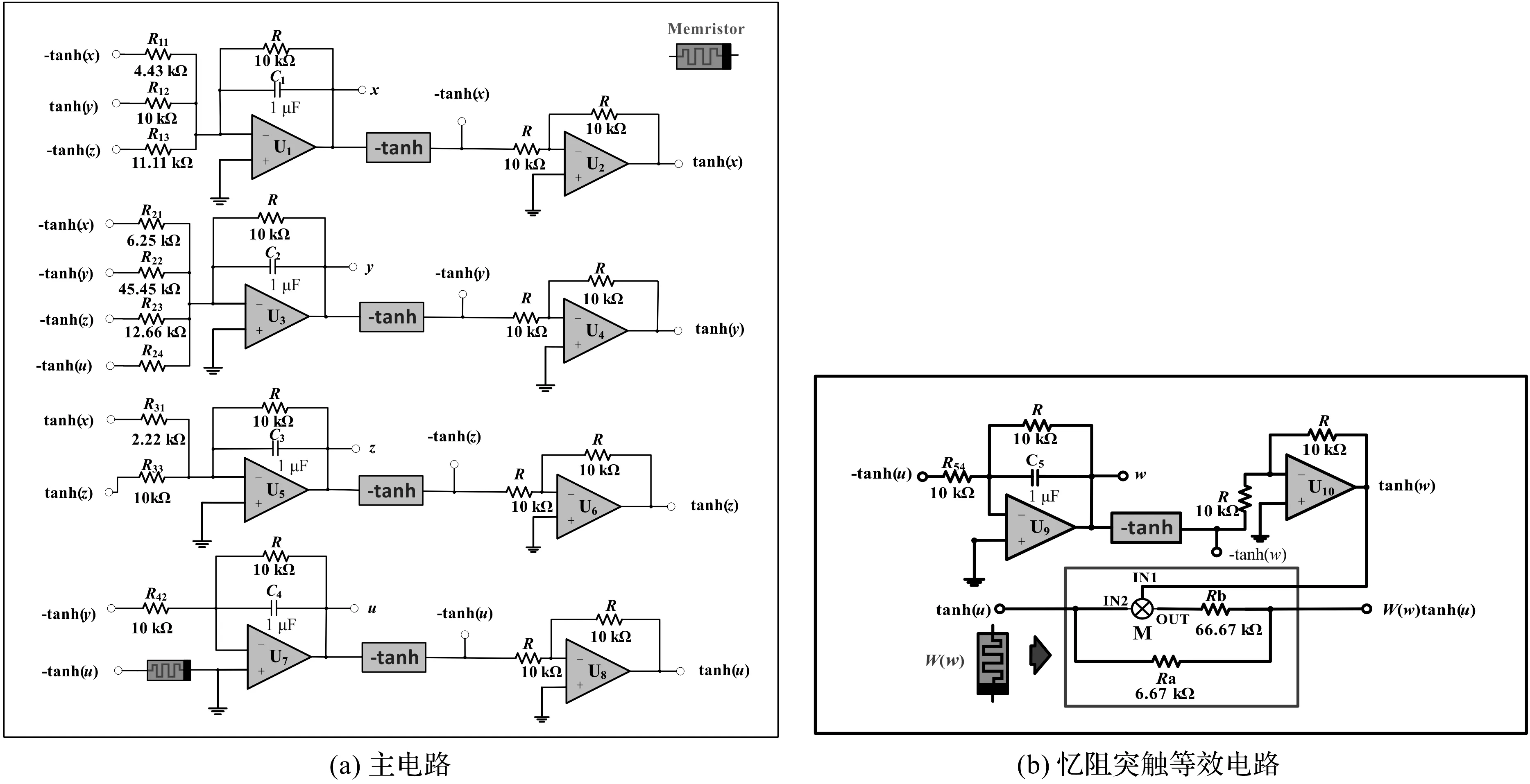
图7 四元忆阻Hopfield神经网络的Pspice电路实现图
固定参数W′44=-1.5,W42=1.0,b=0.1,改变串扰参数W24的值,R24取值分别为2.78 kΩ,2.60 kΩ,2.63 kΩ和2.11 kΩ时,得到Pspice系统仿真电路的相图如图8所示。

图8 四元忆阻Hopfield神经网络随参数W24变化的Pspice仿真相轨图
对比图8与图6可知,电路仿真结果与数值分析结果基本一致,表明本文所设计的四元忆阻Hopfield神经网络具有可实现性。
5 结束语
根据忆阻器阻值的可调特性,本文设计了一种四元忆阻Hopfield神经网络。数学模型分析及Pspice电路仿真实验发现,神经元的串扰行为对神经元的活动产生不可忽略的影响,使神经网络产生一系列复杂动力学行为,表明忆阻Hopfield神经网络在模拟大脑神经活动和记忆行为等方面具有良好的前景。另外,激活函数的选择对Hopfield神经网络性能的影响不容忽视,选择何种更好的激活函数以提高神经网络的性能是下一步研究重点。
