基于B 样条曲线的水稻叶片可视化建模

唐子宗 吴盼盼 杨乐,2* 王映龙,2 张欢欢 施俊林

（1 江西农业大学计算机与信息工程学院 南昌 330045；2 江西省高等学校农业信息技术重点实验室 南昌 330045；第一作者：809894495@qq.com；*通讯作者：jxnzhyangle@163.com）

随着农业信息技术和计算机图形学的发展，目前已经可以在计算机上实现模拟植物生长发育的过程。通过可视化技术，将采集的数据转换成图形信息显示在计算机屏幕上，精确的虚拟作物模型有望为作物群体冠层结构的优化、结构-功能模型以及理想株型设计等方面提供理论支持[1]。虚拟植物已成为目前农业科技领域和图像处理中的研究热点之一。水稻在生长发育过程中会受到温度、土壤养分等因素的影响，是一个极复杂的系统过程。水稻叶片是其进行光合作用、营养物质生产与传输的主要器官，借助计算机技术建立叶片可视化模型，可为水稻的科学栽培和产量提高提供辅助决策。叶片可视化建模这一领域，国内外已做过许多研究，如REFFYE 等[2]采用随机过程方法对植物结构进行仿真；PRUSINKIEWICZ 等[3]通过算法实现了L 系统；KAANDORP[4]采用分形方法对植物的生长与形态进行建模；杨红云等[5]运用Bezier 曲线描述了水稻叶片的边缘信息，并用一元二次方程模拟主叶脉曲线；刘晓东等[6]用基于NURBS 曲面的方法进行水稻叶片的可视化建模；石春林等[7]对水稻形态进行建模及对其虚拟生长进行研究。

目前，对水稻叶片可视化建模的研究及对其建模的方法有很多种，而使用B 样条曲线对水稻叶片可视化建模的研究并不多。在前人研究的基础上，本文改进了水稻叶片可视化建模的方法，降低了水稻叶片数据获取的难度，运用B 样条曲线来描述水稻叶片边缘曲线和主叶脉曲线，结合主叶脉积分数学方法，构建基于B 样条的水稻叶片可视化模型。

1 材料与方法

1.1 试验材料

2019年在江西农业大学农学试验站进行两轮水稻栽培试验[8]，在自然条件下测定水稻叶片在不同生长时期的形态结构参数，将统计分析后的试验数据作为构建叶片模型的数据基础[9]。

1.2 试验方法

每天 9∶00 和 17∶00 用设置好相机参数后的佳能EOS6D Markll 数码相机拍摄水稻叶片图像，每天拍取2 张。选取参照物，保证获取水稻长度时，即获取水稻大致轮廓即可，获取水稻宽度时仅需拍摄水稻最大宽度部分。

2 B 样条曲线及其实现

2.1 B 样条曲线

B 样条曲线（B-spline Curves），是为能描述复杂形状并具有局部性质，改用特殊的基函数即B 样条基函数代替Bernstein 基函数。B 样条基函数是多项式样条空间中具有最小支撑的一组基函数，因此也被称为基本样条（Basis Spline）。B 样条曲线其数学表达式为：

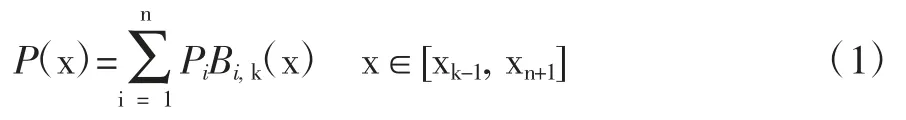
式（1）中，Pi（i= 0，1，… n）是控制多边形的顶点，Bi,k（x）称为 k 阶（k-1 次）B 样条基函数，k 是刻画次数，其中k 可以是2 到n+1 之间的任意整数。

基函数：B 样条基函数是一个称为节点矢量的非递减的参数u 的序列所决定的k 阶分段多项式，这个序列称为节点向量。其递推公式为：

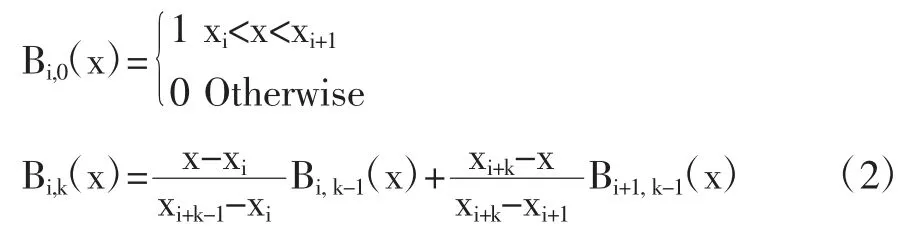
式（2）中，xi是节点值，x=（x0,x1,… xn+k）构成了 k 阶（k-1 次）B 样条函数的节点矢量。B 样条曲线所对应的节点向量区间：x∈[xk-1, xn+1]。

B 样条曲线类型分为4 种，分别是均匀B 样条曲线、准均匀B 样条曲线、分段Bezier 曲线以及非均匀B样条曲线。本文采用了均匀B 样条曲线进行研究，均匀B 样条基函数的节点沿参数轴均匀等距分布，并且均匀B 样条的基函数呈周期性，即所有的基函数有相同形状，每个后续基函数仅是前面基函数在新位置上的重复。

2.2 二次均匀B 样条的实现

n+1个控制点的均匀二次B 样条曲线矩阵表达式为：

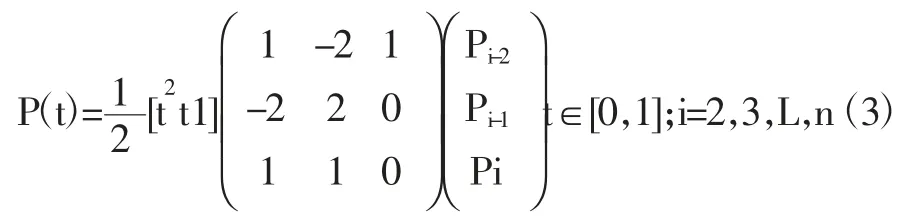
式（3）中，以 4个控制点 P0、P1、P2、P3生成两段二次均匀B 样条曲线为例，由公式3 可求出其一阶导数，控制点 P0、P1、P2确定第 1 段二次均匀 B 样条曲线，P1、P2、P3确定第2 段曲线。第2 段曲线的起点切矢量P1P2沿P1P2边的走向，和第1 段曲线的终点切矢量相等，两段曲线实现自然连接。我们已知控制点的坐标，只需t 取[0,1]上不同的值，就可以绘制出B 样条曲线上各个点，然后将各个点用线段相连，B 样条曲线也就绘制出来了。但为了曲线更加光滑，我们需要尽可能把t 在[0,1]间取更多的值，即间距缩小。二次均匀B 样条在visual studio 2010 中运行结果如图1 所示。

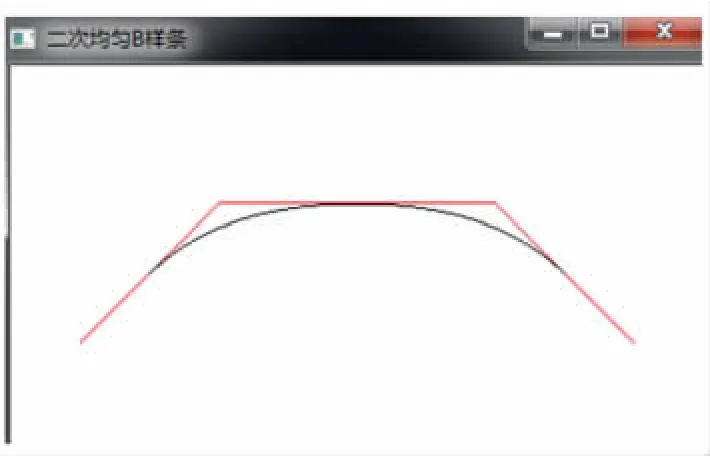
图1 二次均匀B 样条

3 水稻叶片形态计算机仿真

3.1 二维水稻叶片模型的建立及其三角网格化

前期已通过测量得到某一生态环境下水稻叶片叶长为17.5 cm、叶宽0.6 cm 等，如图2 所示。假设水稻叶片的基部位于坐标原点，通过测量最大叶长和最大叶宽得到两者的值，叶脉中心线为坐标纵轴y 方向，它的最大叶宽为叶脉的中心点的反方向，叶片边缘可近似于两段曲线P1P3P2与P1P4P2组成，其中，这4个点的坐标为P1（0，0）、P2（0，17.5）、P3（-0.3，8.75）、P4（0.3，8.75）。绘制一条二次均匀B 样条后，可把这一条曲线视为水稻叶片边缘曲线的一条。再次绘制关于y 轴对称的一条B 样条曲线，即叶片边缘可近似于两条曲线组成。将P1、P3、P23 点代入公式 3，可求出 P1、P3、P23 点组成的二次均匀B 样条的曲线参数方程。同理，将P1、P4、P23点代入公式 3，求出曲线 P1、P4、P2的参数方程。图 3（a）是在VS2010 平台上实现的叶片可视化二维图像。

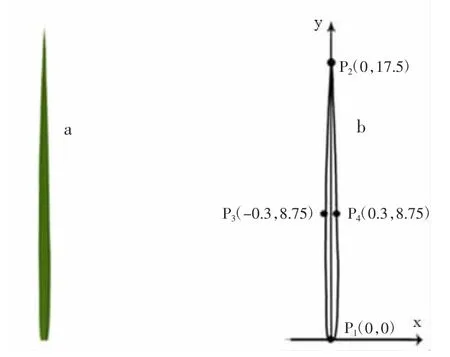
图2 真实水稻叶片（a）及水稻叶片二维模型（b）

图3 水稻叶片可视化模型（a）和三角网格化可视化模型（b）

在绘制B 样条曲线时，两条B 样条曲线上的点的个数是相同的，即i 取相同的值，可代入B 样条曲线方程，得到叶边缘关于y 轴对称点的坐标信息，将左叶片边缘坐标信息存入数组（LXi，LYi），右叶片边缘坐标信息存入数组（RXi，RYi），在平面坐标系中，可近似认为左叶片边缘坐标和右叶片边缘坐标是关于y 轴对称，即两点的中点是在y 轴上，也就是关于主叶脉对称。当取不同的i 值时，可得到曲线上各个点的坐标，最终，将左右叶边缘的点连接起来，将（LXi，LYi）、（RXi，RYi）、（0、RYi+1）3 点连接，则能得到水稻叶片三角网格化模型。在VS2010 平台下，结果如图3（b）所示。

3.2 三维水稻叶片弯曲模型的建立

水稻弯曲真实叶片如图4（a）所示，根据其弯曲图片绘制出概念化模型如图4（b）所示。由于叶片会受到自然环境因素或自身重力的影响发生弯曲。可以采用二次函数来表示叶片主叶脉的伸展方向，该方法较好展示了叶片弯曲效果。但此方法在几何建模过程中，需要获取叶脉与水稻主茎间的夹角来求解该二次函数的系数，而叶片数据测量中获取该夹角的值有一定的困难。这里提出一种基于主叶脉积分的方法进行求解：假设叶片发生弯曲后不会发生折断，叶子P2点的坐标变成P2'（x2,y2）,叶脉长度L=17.5 cm，利用公式4 可求解该二次函数的系数。

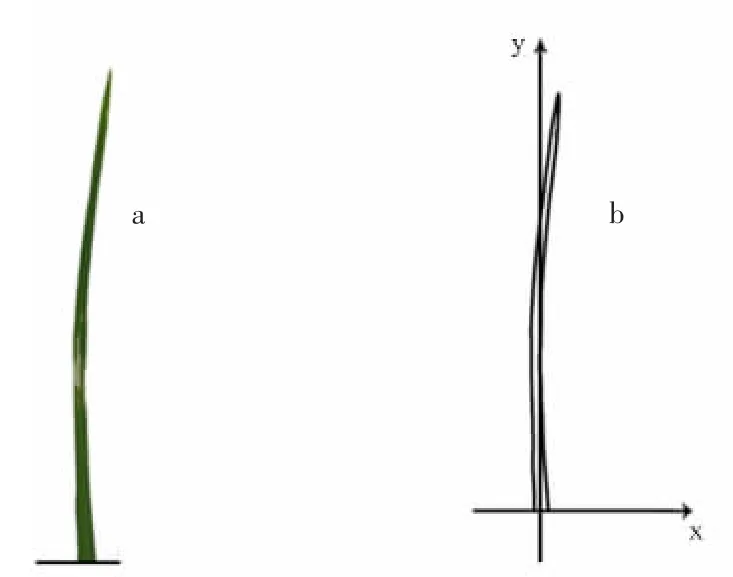
图4 水稻真实叶片（a）及叶片弯曲概念化模型（b）

其系数解的矩阵表达式为：

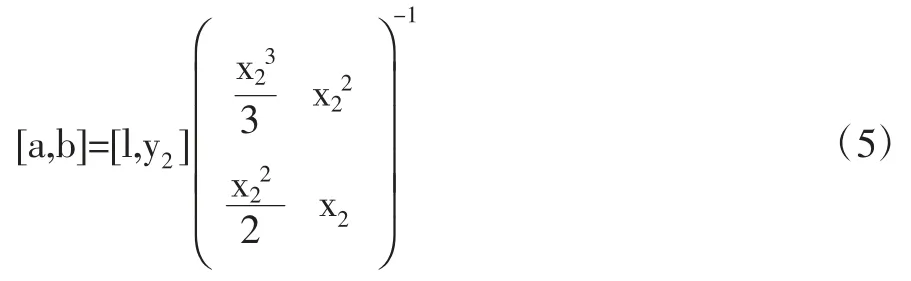
鉴于叶脉弯曲前与弯曲后其插值点到坐标原点的长度保持不变，借助公式6 可求解出叶脉弯曲后插值点的横坐标值。

式（6）中，i∈[1, n]，n 为原始叶脉插值点的个数，为叶脉弯曲前第i个插值点到坐标原点的高度，即该点到叶脉底部的长度，为叶脉底部的第1 点的横坐标值，该值在叶脉弯曲前后不发生改变为求解目标，即叶脉弯曲后第i 点的横坐标值，当全部点的横坐标求解后，再次借助叶脉函数可求解出其纵坐标值。其可视化效果如图5 所示。其中，绘制B 样条曲线的函数代码如下：

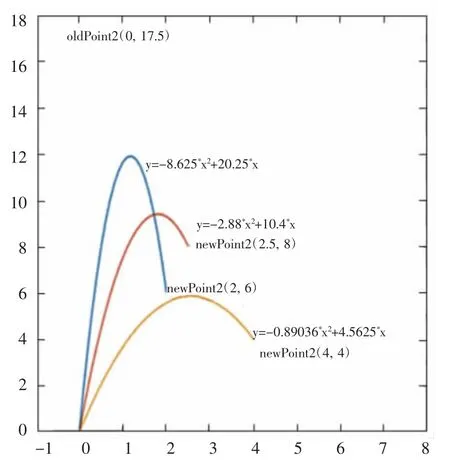
图5 顶点位置展现的叶脉弯曲形态

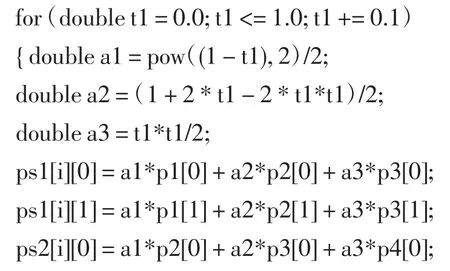
在visual studio 2010 中，只需调整newpoint 叶脉顶点的坐标位置，就能得出不同的弯曲形态。运行该程序，得到的结果如图6 所示。

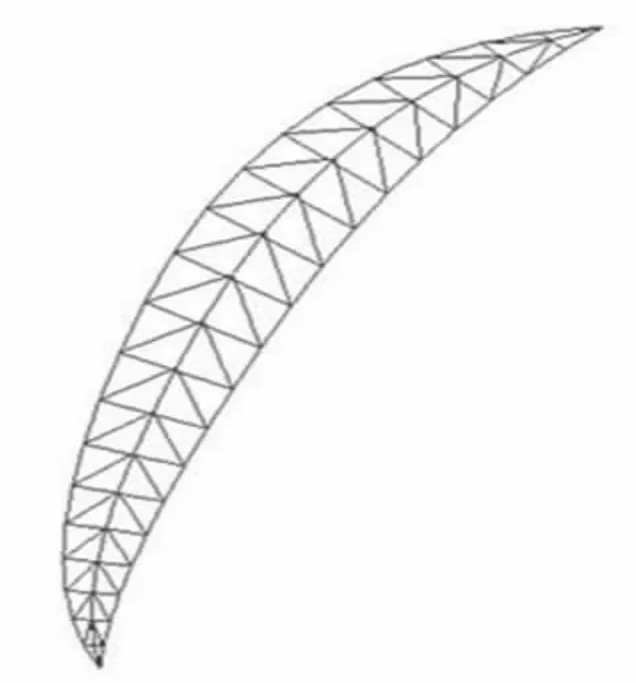
图6 水稻叶片弯曲模型

3.3 试验结果分析

本次试验实现了基于B 样条的水稻叶片可视化建模，在计算机设备上实现了水稻叶片在三维空间上的弯曲。选择3 条B 样条曲线实现对水稻叶片边缘曲线与主叶脉曲线的模拟，并在试验中添加了三角网格化处理，使得叶片更加真实逼真。在水稻弯曲模型的建立中，运用了主叶脉积分的新方法，避免了获取叶脉与水稻主茎间夹角的困难。相较于Bezier 曲线，应用B 样条曲线进行模拟建模更具有优势。例如，Bezier 曲线控制多边形与曲线的逼近程度较差，次数越高，逼近程度就越差；Bezier 曲线不支持局部的修改，调整某一控制点将影响到整条曲线；Bezier 曲线拼接时，满足几何连续条件十分困难。B 样条曲线则在保留Bezier 曲线优点的同时，克服了它的不足。本试验表明，通过调整new－Point 叶脉顶点的坐标位置可以得到不同叶脉弯曲形态，该点坐标值只需通过简单的工具测量获得，而并不需要测量叶脉与水稻主茎间的夹角。

4 结论

本文围绕水稻叶片的可视化建模展开研究，由于水稻叶片的轮廓可用曲线来描述，因此，运用B 样条曲线来可视化叶片边缘，通过二次函数模拟主叶脉弯曲，并提出一种对该函数积分的方法求解弯曲后主叶脉的新坐标值。结果表明，运用B 样条曲线来描述水稻叶片边缘叶脉和主叶脉信息的方法，能够较好反映叶片的特征，使水稻叶片的三维可视化建模仅与叶脉的边缘曲线、主叶脉、最大叶宽、最大叶长等信息相关。

本研究对叶片的可控性不高，随着外部环境因素的改变，如积温、N、P、K 等元素、水分、光照等，这些数据的输入难度也大大增加。除此之外，测量与现实中的水稻叶片也存在误差，而依靠测量的数据进行模拟建模，也会产生一部分计算机误差。在以后的工作中，将进一步对模型进行试验，以提高模型的普适性和实用性。