非视距环境下UWB节点的LS定位算法
2022-04-05吴俊康张烈平匡贞伍神显豪张祖琼
吴俊康,张烈平, 匡贞伍, 神显豪, 张祖琼
(桂林理工大学 a.机械与控制工程学院; b.信息科学与工程学院; c.网络与信息中心, 广西 桂林 51006)
0 引 言
相比于Wi-Fi、 射频识别、 超声波等定位技术, 基于超宽带(ultra wideband, UWB)的定位技术具有厘米级精度、 良好的抗分径能力, 抗干扰能力、 强穿透性等优势。这些优势使得UWB技术在复杂环境中具有高可靠性, 更有利于复杂环境下动态数据的收集和对目标的定位[1-2]。由于复杂环境中存在人、 墙体等障碍物, UWB信号在传播的过程中会产生反射, 因此产生了非视距(non line of sight, NLOS)误差、 多径误差等, 其中NLOS误差是最主要的误差, 对测距、 定位和跟踪的精度、 实时性、 鲁棒性都会产生较大影响[3]。
常用的UWB测距方法有两类, 基于基站节点与待测目标的距离关系和基于基站与待测目标的角度关系[4]。其中, 基于基站节点与待测目标的距离关系的典型方法为基于接收信号到达时间法(time of arrival, TOA)、 基于接收信号到达时间差法(time difference of arrival, TDOA)和基于接收信号强度法(received signal strength indication, RSSI)等[5]; 而基于基站与待测目标的角度关系的典型方法有基于接收信号角度法[6]。由于UWB时间分辨能力强, 并且考虑到环境中多径效应、 NLOS误差等影响以及硬件设备的制作成本, 基于TOA和TDOA的方法广泛用于UWB测距。基于TOA测距算法本质上是对标签到基站距离方程求解, 常见基于TOA测距的定位算法有最小二乘法、 泰勒级数和三边质心定位算法[7]。TS定位算法具有不错的定位精度和鲁棒性, 但需要设置初值, 若初值选择不合适, 可能导致算法不收敛。三边质心定位算法只能用于3个基站节点的定位, 结构比较简单, 无法利用冗余测距信息来提高精度。LS定位算法凭借具有三边质心定位算法类似的定位精度, 不需要设置初值, 并且基站节点越多定位精度越高等特点, 是应用较为广泛的定位算法之一[8]。
本文以NLOS环境下的UWB节点定位为研究背景, 对其中的基于TOA的双边双向测距(double-sided two way ranging, DS-TWR)方法和LS定位算法进行研究, 以期提高UWB定位精度。
1 UWB节点测距方法
1.1 TOA测距方法
图1为二维TOA测距原理图。基于TOA测距方法是在基站节点与标签节点都进行时间同步后, 通过测量标签节点发送UWB信号到达每个基站节点的时间来进行测距的, 即di=cti(ti为标签节点MS到基站节点BSi之间UWB信号传播需要的时间,di为标签节点到基站节点的距离,c表示无线电信号传播速度)。最后以每个基站BSi为圆心,ri为半径画圆, 所有圆的交点为标签位置坐标。
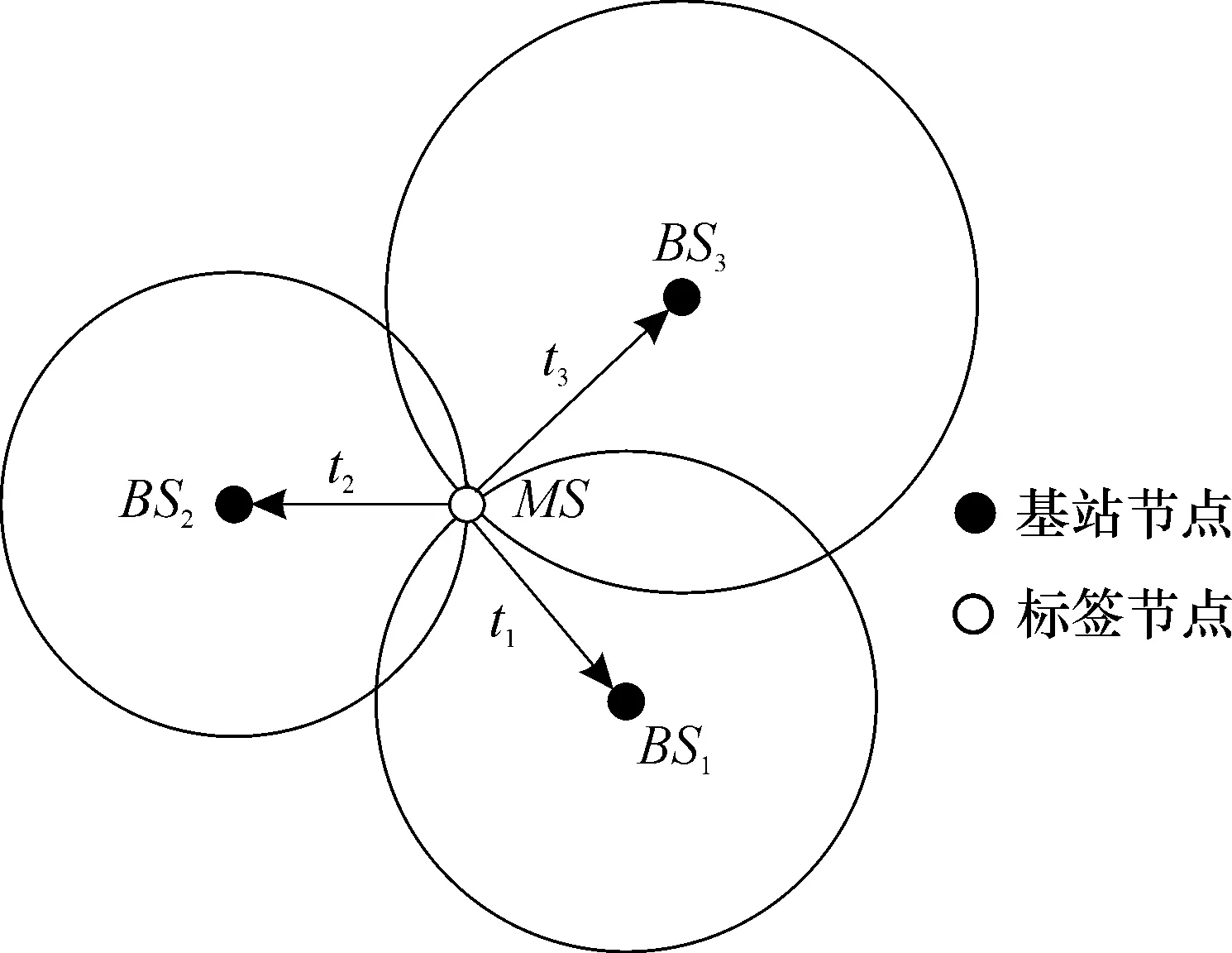
图1 TOA二维测距原理图
在TOA二维定位中, 有3个基站节点, 每个基站节点坐标为BSi(xi,yi), 其中i=1, 2, 3,标签节点的真实坐标位置为MS(x,y)。 定位过程中, 基站节点BS1、BS2、BS3会得到MS发送信号到达时间t1、t2、t3, 则每个基站与标签之间距离di=cti, 于是可得出标签到基站的距离方程, 求解式(1), 便能得出定位标签位置坐标。

(1)
1.2 DS-TWR测距方法
基于TOA的对称双边双向测距算法(symmetrical double-sided two way ranging, SDS-TWR)可以有效解决TOA定位方法需要时间同步和设备时钟漂移等关键技术问题, 使得TOA方法在UWB定位和跟踪研究中受到的关注度最高[9]。SDS-TWR的测距原理图如图2所示。

图2 SDS-TWR测距原理图
SDS-TWR算法测距过程中, 节点A向节点B发送测距信号, 并记录下发送信号时间Ta1; 节点B在接收到测距信号后记录下信号到达时间Tb1并在间隔Treply1后向节点A发送确认UWB信号, 在发送时记录下发送时刻Tb2; 节点A收到节点B发送信号后记录下接受时刻Ta2, 随后节点B反向测距, 在Tb3时刻向节点A发送测距信号; 节点A在Ta3时刻接受到信号并在间隔Treply2后向节点B发送UWB信号, 记录下发送时刻Ta4; 节点B在接收到信号记录下到达时刻Tb4;节点A与节点B经过4次通信后, 可以得出Ttof的值:
(2)
其中,Tround1=Ta2-Ta1;Tround2=Tb4-Tb3;Treply1=Tb2-Tb1;Treply2=Ta4-Ta3。
假设节点A的频率偏差为eA, 节点B的频率偏差为eB, 则信号在空中传播的实际时间Tr为
(3)
则传输时间误差ΔT为
(4)
由于Treply1和Treply2远大于Ttof, 因此eA×Ttof及eB×Ttof可忽略不计, 则
(5)
双边测距算法具有很高的测距精度, 但其测距需要进行4次通信, 测距速度慢、 标签功耗大。针对这些不足, 本文采用DS-TWR算法进行测距[10], 把3次TOA时间求平均后作为最终TOA时间, 从而将SDS-TWR测距需要4次通信降为3次, 以提高测距效率、 减小测距的误差。DS-TWR测距方法的测距原理如图3所示。
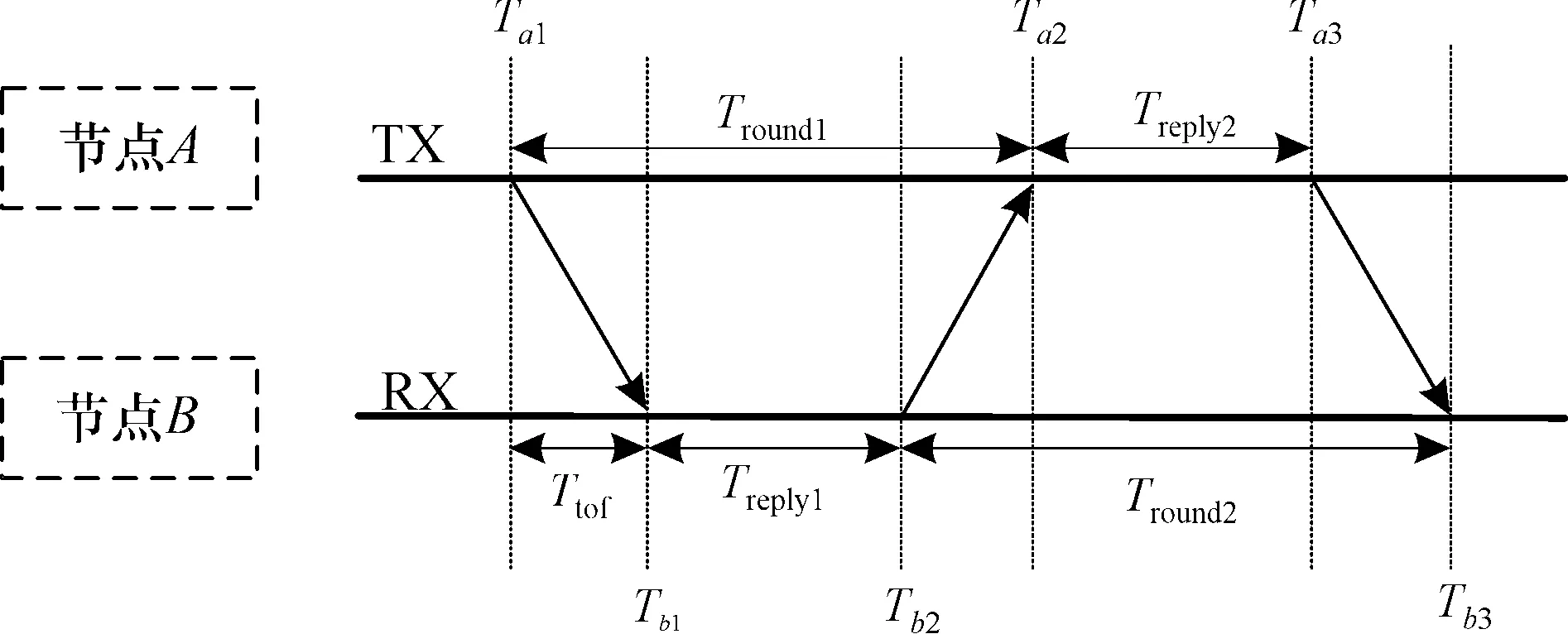
图3 DS-TWR测距原理图
DS-TWR测距过程可以描述为: 节点A向节点B发送测距信号, 并记录下发送信号时间Ta1; 节点B在接收到测距信号记录下信号到达时间Tb1后, 在间隔Treply1后向节点A发送确认UWB信号, 并在发送时记录下发送时刻Tb2; 节点A收到节点B发送信号后, 进行类似节点B的操作, 记录下接收时间Ta2, 延迟时间Treply2后, 再次发送节点B信号, 并记录发送时间Ta3; 节点B再次在接收到信号后记录下信号到达时间Tb3。节点A与B经过3次通信后, 可以得出Ttof的值:
(6)
其中:Tround1=Ta2-Ta1;Tround2=Tb3-Tb2;Treply1=Tb2-Tb1;Treply2=Ta3-Ta2。
由于Tround1=Treply1+2Ttof,Tround2=Treply2+2Ttof, 因此有
=Ttof。
(7)
假设节点A与节点B存在时钟偏差, 并且当前偏离时钟为原来时钟的ka、kb倍, 于是时钟偏移带来误差可表示为
(8)
由于时钟偏移在实际硬件系统是非常小的, 因此ka与kb的值都接近于1, 并且Ttof的实际值通常是纳秒级别的, 因此当基站、 标签数目不多情况下, DS-TWR测距方法不仅可以消除时钟同步带来的测距误差, 还可以抑制时钟漂移带来误差。
2 UWB节点定位的最小二乘法算法
2.1 UWB节点定位过程
UWB节点定位过程如图4所示。在定位区域安放3个已知坐标位置的基站节点, 以及用于人员、 车辆或物品携带的定位标签节点。每一个标签节点都有唯一的ID号, 可通过这个ID号将定位对象联系起来, 使基站节点通过标签节点找到定位对象的位置。在定位过程中, 标签节点不断地与各个基站节点进行通信, 基站节点根据标签节点发射信号到达基站时间、 角度、 信号强度等获得标签与基站节点之间距离信号, 将得到的距离信息代入定位解算算法, 完成标签节点位置估计。一般来说, 基站节点数量越多, 定位精度越高。
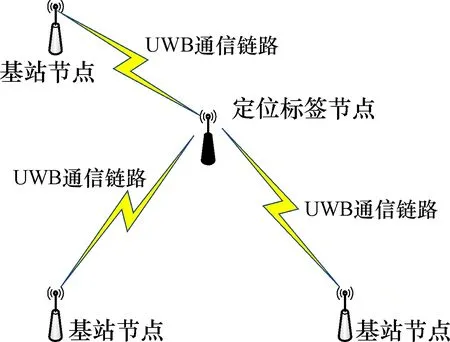
图4 UWB节点定位过程示意图
2.2 最小二乘法定位方法
由于标签到基站距离方程是关于x、y的二次方程, 需要对式(1)等号两边同时平方来消除非线性项:
(9)
用第2、 3个方程依次减去第1个方程, 得到
(10)
为了方便求解, 可将其转换成线性方程组矩阵形式:
ΑX=b,
(11)
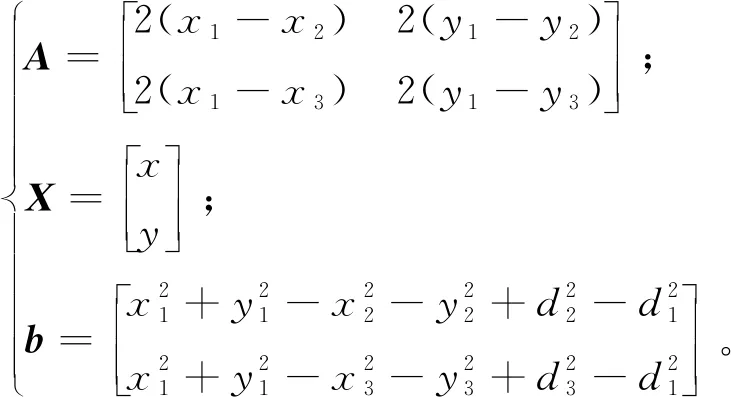
(12)
对式(11)及式(12)用最小二乘法原理, 就可以得到标签的位置估计
X=(ATA)-1ATb。
(13)
2.3 UWB定位性能指标
为了更好地评价定位方法的性能, 需要建立合适的精度指标。 目前常用的指标有均方误差(MSE)、 均方根误差(RMSE)、 累积分布函数(CDF)、 克拉美罗下界(CRLB)等。
1)均方根误差(RMSE)。在二维定位中坐标估计的均方误差表示为
(14)
均方根误差为
(15)

2)累积分布函数(CDF)。累积分布函数是用来统计在一定范围内定位误差出现概率, 通常可表示为
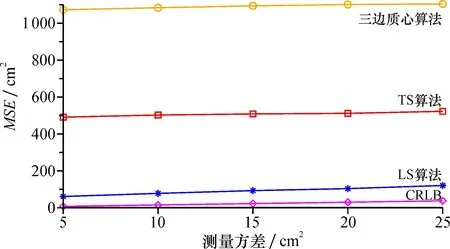
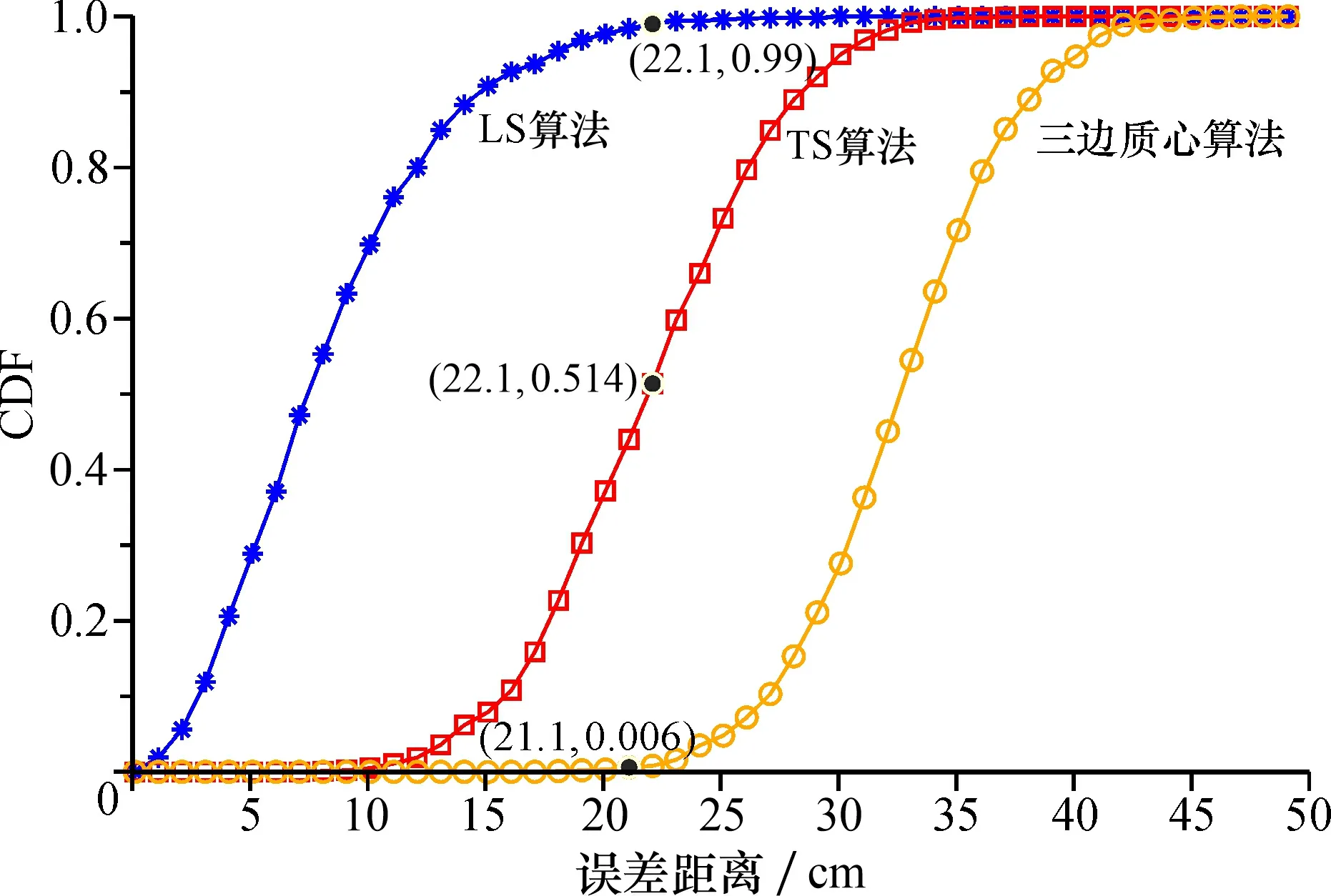
F(x)=P(X (16) 其中:x表示某个定位误差,P(X 3)克拉美罗下界(CRLB)。在参数估计问题中, 采用CRLB为无偏估计量方差的下界, 即方差不可能小于此下界, 在定位研究中通常用MSE与CRLB进行比较。 (17) (18) 其中,I(θ0)是关于θ0的费舍尔信息矩阵(FIM)。 (19) (20) 由式(19)和 (20)可得 (21) (22) (23) (24) 其中,Aij为基站i到基站j的几何状态(图5), 其物理意义为 图5 Aij的几何示意图 (25) 其中:ri,j表示基站i到基站j之间的距离;rij×0为三角形高。由式(24)可知定位精度不仅与测距噪声大小有关还与基站分布有关。 在NLOS环境下, 定位区域定义为200 cm×300 cm, 基站坐标分别为BS1(0,0)、BS2(200,0)、BS3(0,300), 定位标签坐标为MS(100,150)。假设NLOS误差是服从均匀分布, 误差范围为(10,20)cm。采用均方误差、 累积分布函数、 克拉美罗下界3个指标进行评, 评价对象为三边质心算法、 LS算法以及TS算法3种定位算法。图6是NLOS测量误差方差为5、 10、 15、 20、 25时, 3种算法进行1 000次定位后的平均MSE与CRLB比较。图7是测量误差方差为15 cm2时, 3种定位算法的CDF图。 图6 NLOS环境下3种定位算法平均MSE与CRLB对比 图7 NLOS环境下3种定位算法的CDF图 由图6可看出, LS定位算法的MSE与CRLB差值最小, 说明算法的鲁棒性较高。而由图7和表1可以看出LS定位算法在NLOS误差的方差为15 cm2情况下得到CDF相比较其他算法性能表现最好, 小于误差距离22.1 cm的概率达到了0.993; 而同等条件下, TS定位算法概率为0.515, 三边质心定位算法概率仅为0.007。在NLOS定位场景下, LS定位算法定位精度最高, TS定位算法定位精度次之, 三边质心算法定位精度最差, 说明NLOS误差对LS定位算法的定位精度影响较小。 表1 NLOS环境下3种定位算法的CDF 为了实现NLOS环境下UWB节点定位, 本文给出了采用基于TOA的DS-TWR测距算法和LS定位方法相结合的实现方法, 并采用仿真的方法进行了验证。实验结果表明, 相对于其他方法, 本文采用的测距和定位方法在精度上有所提高, 但算法的复杂度较高, 算法的实时性有待进一步提升。下一步工作将针对NLOS误差变化导致UWB节点定位精度下降的问题, 采用模糊推理的方法以缓解NLOS误差, 从而达到减少定位误差的目的, 同时提高算法的实时性。

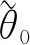


3 实验仿真与结果分析

4 结束语
