桂林地区暴雨天气下两种对流层模型的适用性分析

黄东桂, 刘立龙, 黄良珂, 谢劭峰, 莫智翔

(桂林理工大学 a.测绘地理信息学院; b.广西空间信息与测绘重点实验室, 广西 桂林 541006)

0 引 言

对流层延迟是影响GNSS高精度导航定位的误差源之一[1]。鉴于对流层延迟误差的改正在空间大地测量、 InSAR等应用中的重要性, 国内外学者致力于对流层延迟精细建模的研究, 该模型可分为基于实测气象参数的对流层延迟模型和对流层延迟经验模型。目前传统的基于实测气象参数对流层延迟模型有Saastamoninen、 Hopfield和Black等[2-4], 该类模型在采用实测气象数据时能取得较好的精度, 但在采用标准大气时其精度较差。相比于依赖实测气象参数的对流层延迟模型, 对流层延迟经验模型具有使用简单方便的特点, 如EGNOS模型和UNB系列模型等[5-6], 其中UNB系列模型被应用于美国广域增强系统。上述模型虽能获得相应对流层延迟信息, 但模型稳定性还有待进一步提升。

为进一步满足GNSS用户实时定位导航的ZTD(zenith total delay)改正需求, 诸多学者构建了丰富的区域性和全球性对流层延迟经验模型[7-9]; Böhm等[10]通过对GPT2模型进行改进, 建立了全球区域的GPT2w模型, 该模型目前是最先进的对流层延迟模型之一; 文献[11]基于全球大地测量观测系统(global geodetic observing system, GGOS)资料构建一种基于球谐函数的全球非气象参数GZTD模型, 该模型表现出较好的对流层修正效果; 文献[12]基于ERAInterim再分析资料构建了具有精度稳定等优点的SHAO-H对流层延迟经验模型。

GPT2w和UNB3m作为常用的全球对流层延迟经验模型, 具有使用简便、 适用范围广等优点, 诸多文献研究表明， 两者的模型精度在各区域具有较好的稳定性[13-17], 但在暴雨下模型精度的评估却罕有文献提及, 且相关研究表明暴雨的发生会伴随着ZTD剧烈变化[18], GPT2w模型与UNB3m模型在构建时并未顾及到该类情况, 导致模型存在一定的系统偏差。为此， 本文以GAMIT/GLOBK解算桂林地区CORS基准站的ZTD产品为参考值, 评估桂林地区暴雨天气下对流层延迟模型的适用性, 以期为桂林地区暴雨天气下GNSS的应用提供相应的参考。

1 GPT2w和UNB3m模型和精度评定方法

1.1 GPT2w模型

GPT2w对流层延迟经验模型是由Böhm等基于ERA-Interim再分析资料对GPT2模型进行改进构建的。该模型输入儒略日、 测站经纬度及高程等信息即可得到1°×1°或5°×5°水平格网分辨率的地表气压(P)、 加权平均温度(Tm)、 水气压(es)等气象参数[10]。由于GPT2w模型只提供上述气象参数, 其计算对流层总延迟时需结合Saastamoinen模型计算的天顶静力学延迟(ZHD)和Askne模型[19]计算的天顶湿延迟(ZWD), 方可得到GPT2w模型计算的ZTD。Saastamoinen模型的表达式为

ZHD=2.276 8P/(1-0.002 6 cos 2φ-0.000 28H),

(1)

式中:P为测站地表压强(hPa);φ为纬度(rad);H为测站高程(km)。

Askne天顶湿延迟模型表达式为

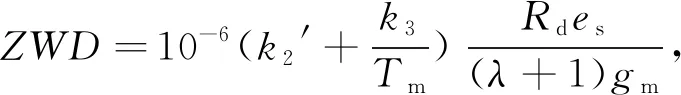
(2)

式中:k2′=16.52 K/mbar;k3=(0.778±0.004)×105K2/mbar;Tm为加权平均温度;Rd为干气体常数;λ为水汽递减因子;gm为重力常数;es为水气压。

GPT2w模型计算ZTD的表达式为

ZTD=ZWD+ZHD。

(3)

1.2 UNB3m模型

UNB3m模型是由加拿大New Brunwick大学将Saastamoinen天顶延迟和Niell投影函数、 气象参数年均值以及振幅表构建的条带模型, 它将美国标准大气资料沿着纬度进行条带化, 得到一个以15°间隔的大气参数表用以估算关键气象参数, 通过输入年积日、 测站纬度、 高程等信息即可得到测站所在位置相应的温度、 压强、 水汽压、 温度梯度(β)、 水汽梯度(即水汽递减因子λ)气象参数, 其中气象参数年均值表和振幅表等信息可参考文献[6]。

UNB3m模型计算ZHD和ZWD的表达式为

(4)

(5)

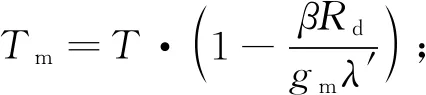
(6)

λ′=λ+1。

(7)

其中，g为地表的重力加速度。结合式(3)得到UNB3m模型计算的ZTD。表1为GPT2w和UNB3对比, 其中dT为温度递减率, 其他参数同前文。

表1 GPT2w模型和UNB3m模型对比

1.3 模型的精度评估方法

模型的评定以ZTD为参考值(真值), 模型计算的ZTD为估计值, 以偏差(BIAS)及均方根误差(RMS)两种精度指标检验模型的精度:

(6)

(7)

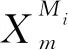
2 GPT2w和UNB3m的适用性分析

2.1 数据来源及处理策略

本文使用GAMIT/GLOBK, 选取桂林地区内的8个CORS站为非固定站, 以BJFS、 CHAN、 SHAO、 LHAZ、 TWTF和URUM为固定站参与联合解算, 得到2017年6—7月的ZTD产品(时间分辨率为1 h)作为参考值用以评估对流层延迟模型在暴雨天气下桂林地区的适用性。图1为桂林地区8个CORS基准站的分布图。

图1 桂林8个CORS基准站点位分布图

2.2 数据源精度评估

为了验证采用GAMIT/GLOBK解算得到的2017年6—7月桂林CORS基准站的ZTD精度, 选取该时间段内IGS站(BJFS、 TWTF)提供的ZTD作为参考值(记为ZTDIGS), 与参与桂林CORS基准站解算的BJFS、 TWTF站得到的ZTD值(记为ZTDCORS)相比较, 把大于3倍中误差的偏差作为粗差予以剔除; 其中IGS站提供的ZTD数据精度为4 mm, 可作为ZTD检验的参考值[17], 检验结果如图2所示。可见, 参与桂林ZTD解算的IGS站观测的ZTD与IGS站提供的ZTD数据具有较好的一致性, BJFS和TWTF站的相关性达到0.98以上, RMS分别为5.3和5.6 mm。因此, 用桂林CORS基准站解算的ZTD产品来评估对流层延迟模型的精度是具有参考价值的。

2.3 模型精度评估

2.3.1 模型偏差和RMS统计 为检验每年6、 7月桂林暴雨季节GPT2w模型和UNB3m模型在桂林地区ZTD的计算精度, 本文选取分布在桂林地区8个CORS基准站2017年6—7月(年积日第152—213天)解算的ZTD数据作为参考值, 对GPT2w模型(由于GPT2w模型具有1°和5°的格网分辨率, 为方便后续描述分别简称为GPT2w-1和GPT2w-5)及UNB3m模型计算的ZTD进行精度检验, 并对8个测站的偏差和RMS进行月统计, 结果见表2。

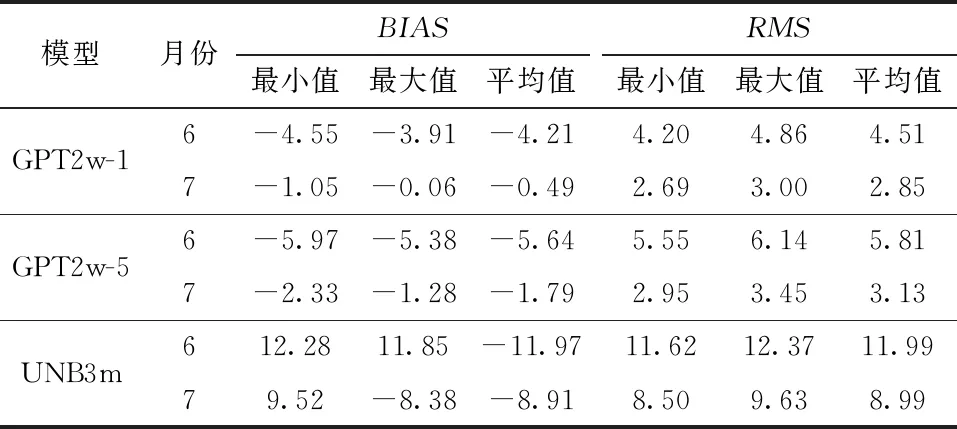
表2 各模型2017年6、 7月的BIAS和RMS统计

各模型在桂林地区整体上呈现出负偏差, GPT2w-1、 GPT2w-5和UNB3m模型最大负偏差均出现在6月, 其值分别为-4.55、 -5.97和12.28 cm, 而GPT2w-1模型最大月均偏差值小于GPT2w-5和UNB3m模型; 各模型的RMS最小值均出现在7月, 其值分别为2.69、 2.95和8.50 cm, UNB3m模型表现出更大的月均RMS, 其最大值可达12.37 cm, 大于GPT2w模型的RMS最大值(4.86～6.14 cm)。综上所述, GPT2w-1模型表现出较好的精度, 各模型在7月的精度要优于6月的精度, 主要是6月份的极端天气较多, 造成模型在该区域出现一定的系统性偏差, 导致模型稳定性相对较差。

2.3.2 对流层延迟模型日偏差与降雨量的时间序列 与桂林CORS站并址的8个气象站实测降雨量数据显示, 在年积日177—185中桂林地区存在暴雨天气(24 h内降雨量超过50 mm的强降雨过程)。 为验证暴雨与对流层延迟模型的影响, 以年积日177—185为例, 得到对流层延迟模型的日偏差与降雨量的时间序列, 结果如图3所示。

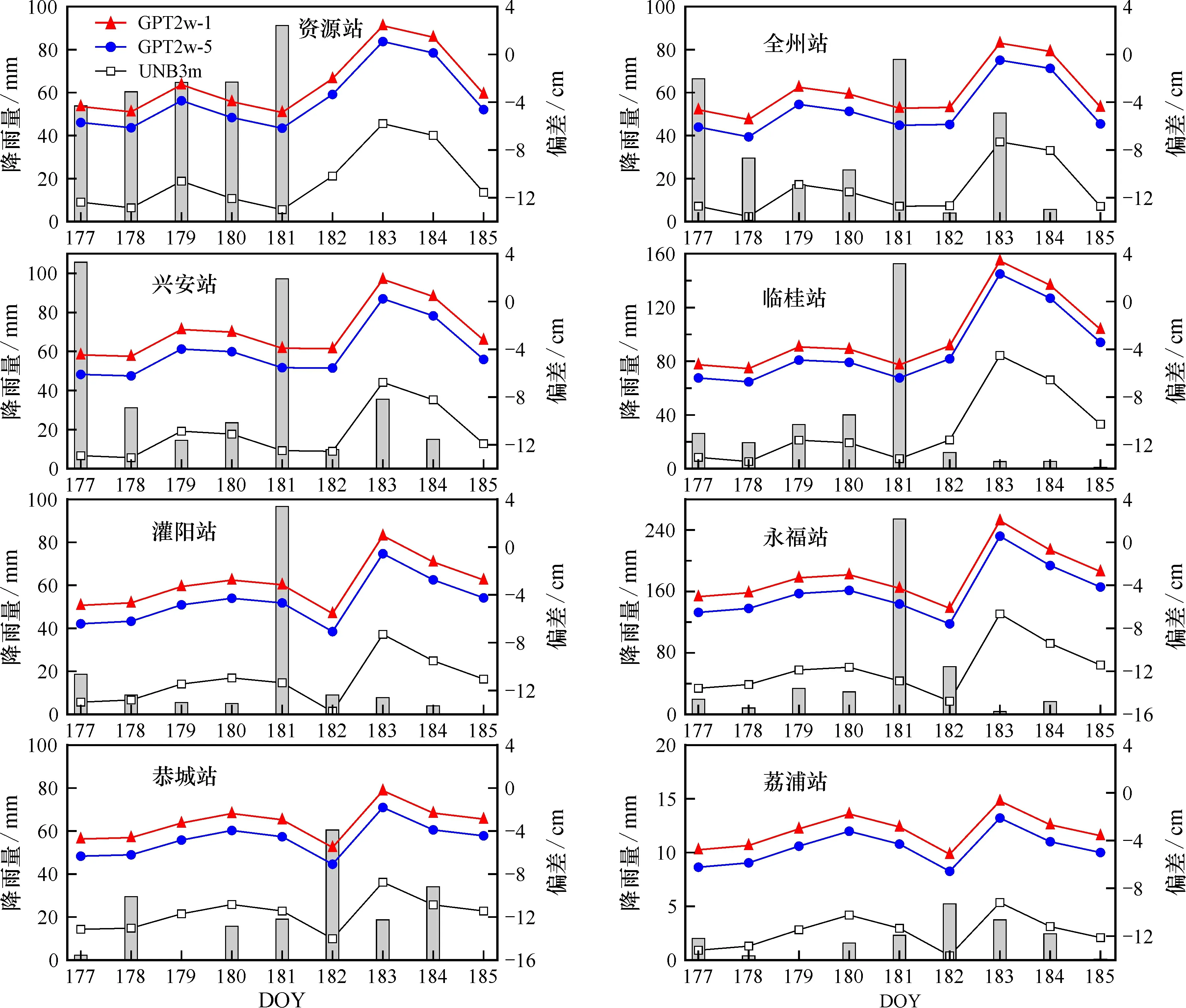
图3 模型日偏差与实际降雨量时序分布比较

可知, 在年积日177—180天, 在降雨量较少的测站中模型日偏差变化较为平缓, 如灌阳站和永福站, 而在降雨量较多的资源站中模型日偏差较于前者表现出更大的波动; 在第181天内存在暴雨天气的测站中, 各模型日偏差值在48 h内呈现较大的波动, 降雨量较多的永福站和临桂站表现较为显著, 其中各模型在临桂站中最大日偏差变化量为8.7 cm, 而降雨量较少的灌阳站为6.5 cm。整体上, GPT2w和UNB3m模型的日偏差变化趋势基本一致, 部分测站的降雨量对模型日偏差存在显著的影响。

2.3.3 暴雨前后24 h精度评估 为分析暴雨前后24 h对流层延迟模型的精度, 选取年积日第181天(暴雨)前后24 h降雨量较少的临桂站为例, 以6 h为时间间隔对对流层延迟模型在临桂站年积日第180、 181和182天的精度进行统计, 得到暴雨前后临桂站模型偏差和RMS时间序列图, 如图4所示。可知, UNB3m模型相比于GPT2w模型表现出较大的偏差和RMS值; 在暴雨前, 各模型偏差和RMS值保持着相对稳定的水平; 在第181天中, 临桂站的偏差呈现缓慢递增的趋势, 在24 h中达到最大偏差, 随后24 h内, 偏差呈现缓慢递减的趋势, 随后在182天的12:00—18:00时中, 偏差具有显著的递减趋势, 同时RMS也具有相同的变化特征， 说明对流层延迟模型在暴雨前后的精度会受到一定程度的影响, 主要原因是对流层延迟模型在建立时未考虑极端天气下(暴雨)会导致模型出现显著的系统性偏差, 对模型的稳定性造成相对的影响。

图4 暴雨前后24 h各模型BIAS和RMS时间序列

2.3.4 不同天气下模型的残差统计 为进一步分析对流层延迟模型在暴雨天气下的适用性, 选取晴朗天气(年积日第201—209天)与存在多日降雨天气(年积日第177—185天)为时间段, 分别对GPT2w-1、 GPT2w-5和UNB3m模型估算的ZTD与桂林CORS基站解算的ZTD产品进行逐小时对比, 统计各模型与CORS基准站的残差(模型值与参考值之差), 结果见图5。

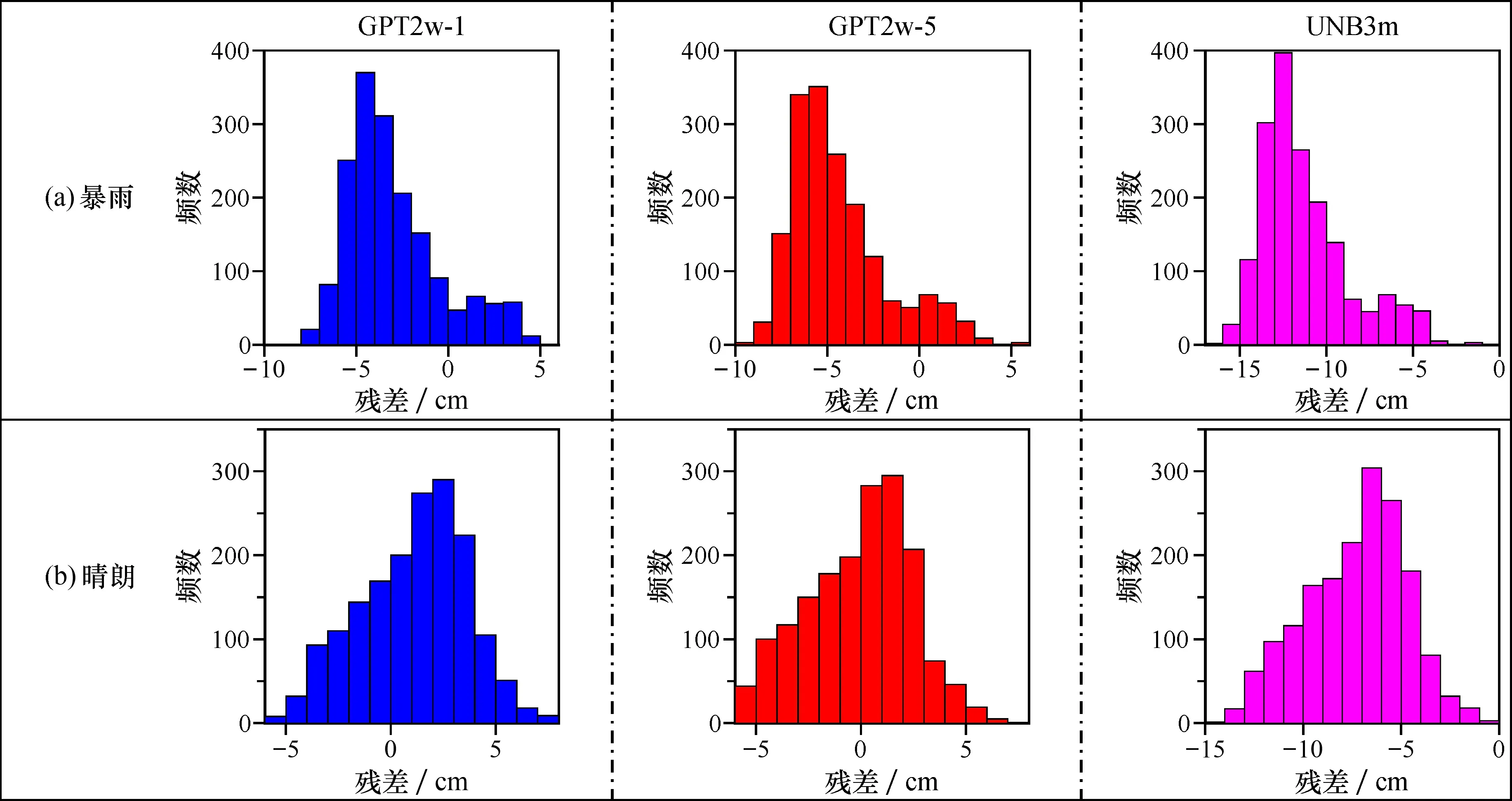
图5 暴雨(a)和晴朗(b)天气下各模型计算ZTD的残差分布直方图

对比可知, 在暴雨情况下GPT2w模型残差整体上表现为负残差, 而UNB3m模型在晴朗和暴雨天气情况下均表现出负残差值, 在暴雨的情况下表现出更大的负残差， 其中GPT2w两种分辨率的模型残差主要集中在5 cm左右; UNB3m模型残差较于GPT2w模型显著, 主要集中在13 cm, 残差较大。GPT2w模型在晴朗天气下的残差主要集中在3 cm左右, 而UNB3m模型主要分布在6 ～ 7 cm, UNB3m模型较于GPT2w模型表现出较大的残差, 进一步表明GPT2w模型的性能优于UNB3m模型, 且各模型在晴朗天气下的残差值要小于暴雨天的残差值。

2.3.5 不同天气下模型的平均偏差和RMS统计分析 为进一步对GPT2w-1、 GPT2w-5和UNB3m模型在暴雨天气下的适用性进行分析, 以上述18 d为时间段, 对8个CORS站对应的偏差和RMS取均值, 得到桂林地区平均偏差和RMS的时间序列, 结果见图6。

在暴雨天气下(图6a)各模型整体上呈现出负偏差, GPT2w-1和GPT2w-5和UNB3m的平均偏差分别为-2.94、 -4.37和11.26 cm, RMS分别为3.77、 4.86和11.37 cm。UNB3m模型相较于GPT2w-1和GPT2w-5表现出更大的负偏差和RMS, 最大值分别为-13.1、 13.12 cm; 而GPT2w-1模型与GPT2w-5模型的偏差和RMS均小于7 cm。 从整体上看, GPT2w模型在暴雨天气下的精度要优于UNB3m模型。在晴朗天气下(图6b)UNB3m模型整体上呈现出了负偏差而GPT2w-1与GPT2w-5模型呈现出较小的负偏差和正偏差; 其中GPT2w-1和GPT2w-5模型的平均RMS分别为2.59和2.34 cm, 而UNB3m模型平均RMS为7.45 cm。

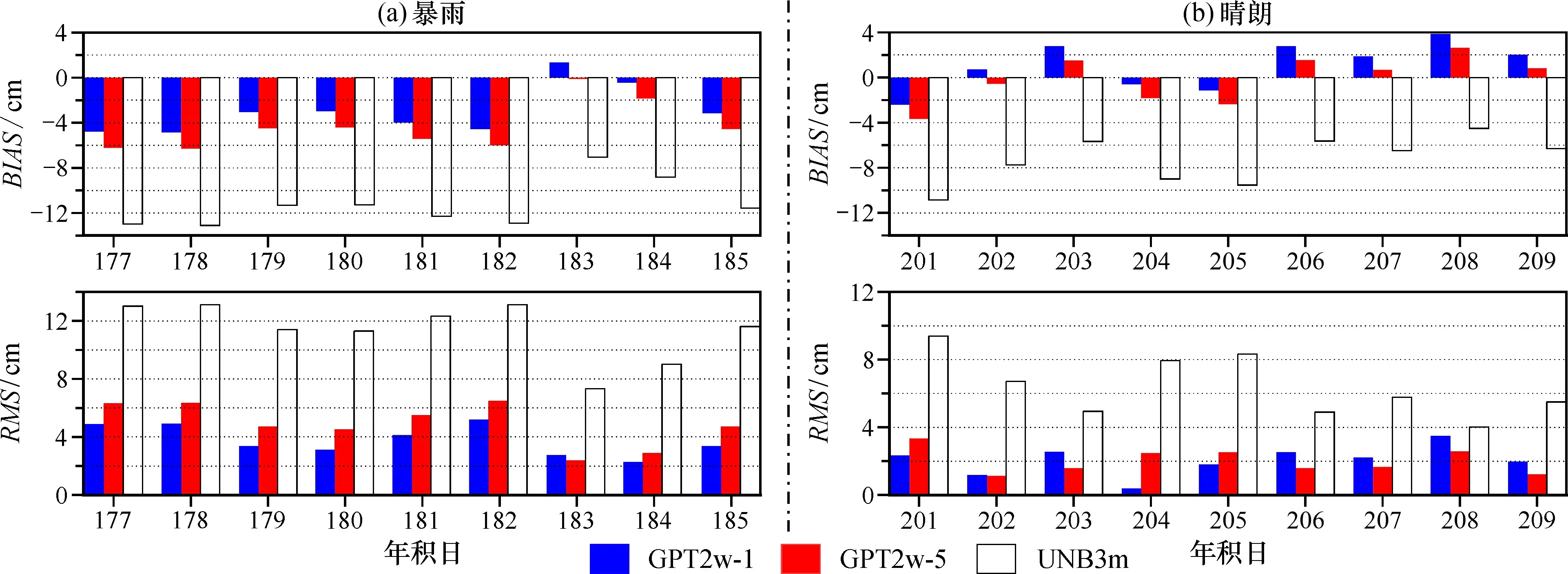
图6 不同天气下各模型BIAS和RMS时间序列

对比发现, 在晴朗天气下各模型的偏差和RMS值均小于暴雨天气, 且偏差和RMS波动较小， 说明在晴朗天气下模型的精度及稳定性要优于暴雨天气下模型的精度。 此外, GPT2w模型在晴朗天气下和暴雨天气下的精度普遍优于UNB3m模型。

3 结束语

本文采用CORS基准站解算的ZTD产品对GPT2w和UNB3m模型在桂林地区暴雨天气下的适用性进行评估, 结果表明:

(1)GPT2w模型在不同天气下的精度及稳定性要优于UNB3m模型, UNB3m模型在暴雨天气下和晴朗天气下都表现出较大的偏差和RMS, 主要原因可能为UNB3m模型为条带模型, 格网分辨率较低且未考虑到经度变化及未顾及湿度梯度等因素。

(2)GPT2w和UNB3m模型在晴朗天气下的精度普遍优于暴雨天气下的精度, 其中暴雨天气下GPT2w模型的偏差和RMS均优于7 cm, 而UNB3m表现出更大的偏差和RMS。

综上所述, 在桂林地区暴雨天气下GPT2w模型相较于UNB3m模型具有较好精度及稳定性, 可满足暴雨天气下导航定位的需求和应用。