泵送混凝土管道冲蚀疲劳失效数值模拟

孙语晨, 张玉波, 李 靖, 南 轩, 袁玉麟

(云南农业大学 a.建筑工程学院; b.云南省高校城乡水安全与节水减排重点实验室, 昆明 650201)

0 引 言

随着我国大型基础建设工程的快速发展和水利设施的大规模建设, 对泵送混凝土这一技术的发展有了极高的要求。由于混凝土的泵送过程是一个多相稠密非牛顿流体流动过程[1], 且混凝土黏度极大且颗粒含量较高, 极易导致管道冲蚀疲劳破损。在高速介质流动中, 冲蚀和空蚀问题相较于腐蚀问题破坏更加迅速, 对设备及管路的安全运行影响更为明显。相关的调查表明: 冲蚀磨损占整个工业磨损的8%, 主要是固体颗粒间的相互作用在管道内形成摩擦和冲蚀磨损, 特别是弯管处的颗粒比直管段高出50倍左右[2]。

混凝土泵送过程中颗粒对金属表面冲蚀作用的影响因素主要包括: 颗粒尺寸、 管壁材质、 管壁的曲率以及环境介质等[3]。颗粒撞击在金属表面形成粗糙磨损层, 随着撞击次数增加, 表面金属层不断被剥离形成新的金属结构面, 由于泵送管道的曲率变化(如直管段进出口壁面、 缩颈管段直冲弧面和弯管曲面的凹陷面)导致颗粒撞击管壁的撞击力不同, 最终使得管道壁面的磨损程度差异也较大, 其对管道壁面的疲劳失效位置与疲劳寿命的影响机制是影响管道设计和维护的主要依据。

目前, 对泵送混凝土冲蚀管道的研究相对较少, 谭援强等[4]通过DEM预测离散粒子的运动学和轨迹以及粒子粒子相互作用, 并且通过Navier-Stokes求解器评估连续流体相的运动规律, 并且采用压力梯度力模型来计算固体-流体相互作用力； 程井等[5]针对泵送大体积混凝土绝热温升高、 早期水化速率快的特点结合绝热温升试验构建了基于水化度的水化温升速率模型(简称水化度模型)采用人工蜂群算法对水化度模型、 双曲线模型、 单指数模型和双指数模型参数进行反演对比分析。Huang等[6]对混凝土在弯管泵送时内部所受的应力分布规律进行了深入分析并提出弯管设计改进方法; 李悦等[7-8]对泵送混凝土在泵管中的流动行为进行了模拟, 并提出了混凝土在泵管中的流速、 压力分布及泵送压力损失变化规律; Liang等[9]研究了管砂颗粒对于管道结构和元件的冲蚀。对于复杂结构经受长时间液固两相流冲蚀工况, 颗粒的撞击形式和介质环境对冲蚀结果的影响最为显著, 主要体现在管道壁面的冲蚀磨损是由非牛顿流体-颗粒、 颗粒与颗粒以及颗粒与壁面撞击等相互作用下造成损伤累积直至局部变形、 失效破坏的过程[10-16]。因此, 混凝土在泵送过程中颗粒和流体的运动演化规律比较复杂, 其对壁面的冲蚀磨损机制也有待进一步深入研究。

针对混凝土泵送过程中颗粒的运动演化规律及其对管道的磨损机制以及管道磨损的寿命预测的相关研究还不够系统和深入, 从而严重限制了泵送混凝土的施工应用。本文采用计算流体力学(CFD)和离散单元法(DEM)相结合的方法来分析混凝土泵送过程的流动情况及其对管壁的冲撞磨损规律, 旨在从数值变化的角度分析混凝土泵送过程中颗粒的流动状态及其对管道的冲蚀磨损演化规律。 另外, 通过借助FEA分析预测管道的疲劳寿命, 从而为泵送混凝土施工中存在管道冲蚀磨损等问题提供理论支持。

1 试验部分

1.1 试验模型

采用龙开口水电站使用的碳钢管道进行试验。 试验段管道为管径150 mm, 总长度2 000 mm, 壁厚10 mm的复合不锈钢管道, 管内的流速根据龙开口水电站隧洞现场试验测试值1.811 m/s进行设计, 试验模型如图1所示。

图1 泵送混凝土管段试验模型

1.2 混凝土配比要求

对于混凝土泵送试验颗粒级配与管道直径按照如下标准设计: 粗骨料最大粒径与输送管径之比, 对整体而言不宜大于1∶3, 当输送高度在50 m以下时, 对卵石应小于1∶2.5; 输送高度在50～100 m时, 应在1∶3～1∶4; 输送高度在100 m以上时, 应在1∶4(表1)。

表1 混凝土材料物性参数及颗粒配比

1.3 管道划分与结果测试

为了分析管道的冲蚀磨损变化规律, 对整个管道进行分割测量(每一段长度约400 mm， 共6段，从进料口开始标记), 用电子秤称测量管道的质量, 研究钢管磨损后沿泵送方向质量损失的变化规律。

1.3.1 每段管道磨损变化规律 钢管米重检测结果通过每米损失的质量进行表示, 钢管磨损失重变化及整个磨损情况如图2所示。米重检测结果表明: 钢管弯管段失重最严重, 失重率从进料端的22.8%逐渐降低到钢管直管段中部的20.46%， 并在弯管中部的位置处增加到23.53%。

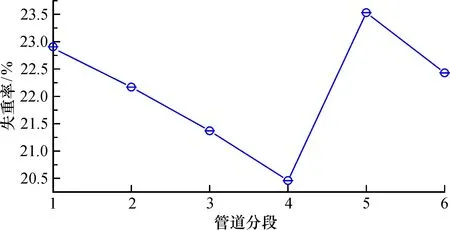
图2 泵送距离与磨损失重变化

1.3.2 钢管复合层厚变化规律 钢管复合层厚变化结果为: 钢管弯管处的焊缝位置(即弯管中部)磨损最严重, 磨损厚度约1.36 mm; 直管段中部的复合层磨损量均匀磨损厚度1.04 mm; 进料端平均磨损1.21 mm。磨损情况如图3所示。

图3 管道中各位置的磨损示意图

综上, 泵送混凝土在泵送过程中颗粒对管壁的碰撞会导致管壁受到不同程度磨损, 磨损后的管道壁面会导致泵送摩擦阻力相应增大, 最终导致泵送管道堵塞, 从而造成施工工期延误进而导致直接的经济损失。由于混凝土泵送过程中颗粒和流体以及管壁间的相互作用机制比较复杂, 因此有必要利用计算流体动力学和离散元法(CFD-DEM)相结合的方法对混凝土泵送过程进行数值模拟, 研究颗粒之间、 颗粒与流体以及颗粒与管壁面的相互作用机制, 同时利用有限元方法(FEM)分析预测管道的疲劳寿命, 为泵送混凝土的设计、 维护以及工程应用提供理论指导。

2 数值模拟

2.1 理论模型

颗粒与流体的相互作用的核心思想是当颗粒团前端颗粒接触壁面时(图4), 开始捕捉与它最近颗粒的位置及运动信息, 同时计算该颗粒的反弹参数(速度及方向)。当前端颗粒i与邻近颗粒j发生反弹碰撞时, 颗粒j方向会发生改变、 动能也会变化, 此时颗粒j碰撞壁面的冲蚀速率与无颗粒碰撞前的差异较大。目前, 在CFD-DEM理论中最常见的控制方程是基于颗粒受力构建的, 且包含了压力梯度力, 在模型中, Ishii形式的动量方程应用较多, 其具体形式为

图4 颗粒之间的作用机理

(1)

可见, 在作用于粒子的力中曳力起主要作用, 因此本文只关注重力和曳力。流体和粒子之间的相互作用则通过广泛使用的Di-Felice阻力模型来描述。

(2)

其中:εf、ρf、uf分别为流体的体积分数、 密度和速度;P为静压力;τf为应力;fdrag表示流体对颗粒的曳力。

(3)

2.2 理论模型修正

对于泵送混凝土, 由于颗粒的体积已经大于或者接近于网格体积, 导致现有的CFD-DEM理论无法得到准确的计算结果, 但混凝土的泵送过程是液体介质携带固体颗粒以一定的角度和速度对材料表面进行冲击磨损的过程, 这种冲速不高的浆冲蚀磨损主要是由固体颗粒造成的[17-20]。

本文只选取长度为1 350 mm的直管和外半径650 mm的弯管(图1)组成计算模型, 因此, 在CFD-DEM耦合过程中颗粒数量有限, 为了满足CFD-DEM耦合过程中体积分数的要求, 文中采用颗粒替换模型, 即用颗粒体积为网格体积1/3的颗粒替换超过网格体积1/3的颗粒。另外, 为了使颗粒在高黏度的混凝土浆体中保持较高的计算准确性, 文中参考了非牛顿流体颗粒的阻力曲线来对曳公式进行修正处理。

2.3 模型建立

按照龙开口水电站隧洞泵送混凝土施工建立管道有限元模型(图5), 直管段长1 350 mm、 弯管处外半径650 mm、 管径150 mm、 壁厚10 mm, 网格数为53 450, CFD的进口边界条件为泵送速度条件进口, 并且保证CFD-DEM耦合数值模拟的网格无关性要求[15-19]。对于未解析CFD-DEM, 首先是要保证网格尺寸大于颗粒尺寸， 上述已经说明了采用颗粒替代的方法进行处理, 在此基础上采用0.75和1.5 cm的网格进行对比测试监测相同位置处的流场参数变化结果, 流速分别为1.53和1.61 m/s, 误差约0.05 m/s, 该误差值能够满足流场收敛性的标准符合文献[15-19]中对网格收敛性的要求。

图5 龙开口隧道泵送混凝土施工管道网格模型

为了进一步研究混凝泵送过程中各部位的冲蚀状况, 在CFD-DEM模型中, 将水和灰看作流体用于CFD计算, 而DEM中粗骨料和细骨料的物性参数则为试验和工程中所使用骨料的材料参数。

2.4 骨料的模型及参数

通常情况下混凝土和宾哈姆流体比较接近, 但目前还没有比较成熟的非牛顿流体曳力模型。因此, 选用高黏度流体来模拟混凝土的流变特性, 即把泵送混凝土看作高黏液体在推力作用下沿着输送管道的流动。在数值模拟过程中, 将混凝土模型简化为粗骨料、 细骨料以及水泥砂浆3部分, 采用不同粒径的的球形颗粒代替不同尺寸的骨料, 骨料粒径分别为5、 15和25 mm。对于颗粒的独立撞击, 冲蚀计算时只用考虑每个颗粒的撞击参数; 而对于颗粒的干扰碰撞, 则需要捕捉受干扰颗粒撞击后的位置和运动参数。因此, 在颗粒与壁面距离较近时, 须根据颗粒直径和运动速度对网格进行适当局部加密。

施工时混凝土温度设置20 ℃、 水泥浆的密度为1 600 kg/m3、 动力黏度为21 Pa·s、 粗细骨料等动力黏度和配比符合要求泵送要求, 颗粒冲蚀数值模拟受颗粒参数、 流体流动参数和壁面材料特性参数共同影响, 其中, 颗粒的密度、 粒径和流体流动压力、 流速直接影响颗粒运动轨迹, 从而改变颗粒撞击壁面时的动能。当颗粒在撞击壁面过程中受到其他颗粒干扰时, 会改变其运动状态, 从而影响冲蚀速率, 因此在DEM中颗粒表面摩擦参数的设置极为重要, 根据文献[14-22]和龙开口隧洞施工中现场测试粗骨料(卵石)和细骨料(中砂)的颗粒表面参数见表2。

表2 不同粗骨料和细骨料混凝土模型的参数值

2.5 模拟结果及分析

2.5.1 颗粒的运动规律及其对管壁的冲击作用 基于EDEM 与FLUENT联合仿真的方法, 在FLUENT中使用双精度稠密颗粒流动模型, 在EDEM中使用离散元模型追踪固体颗粒群的运动过程。为了探究该耦合模型中离散化固体颗粒运动演化规律及其对管道内部管壁的冲击磨损机制, 首先讨论了颗粒在管道内部的运动演化规律, 如图6所示。颗粒的运动速度随管道的曲率变化而变化, 曲率越小颗粒的流速越快; 同一个截面上, 靠近管壁的颗粒速度相对较低, 而在管道中间的颗粒的运动速度相对较大, 这主要是因为管壁阻力限制了颗粒的流动。

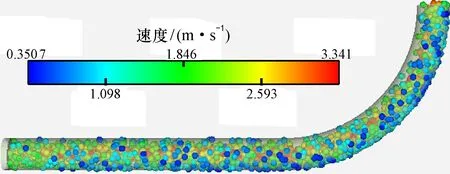
图6 泵送过程中管道内部颗粒运动情况

图7为颗粒在管道内部的流动对管壁的冲击力的模拟结果。可以看到: 混凝土在泵送过程中直管段管壁受到颗粒的冲击作用较小, 尤其是在入口处最小; 而在弯管处的外圈管壁(外凸面)受到颗粒冲击的作用最大, 因此可以得出结论——弯管壁面外圈管壁最容易被颗粒碰撞磨损。

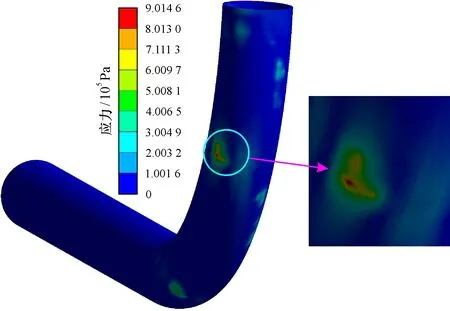
图7 管道内部管壁受力情况

2.5.2 颗粒间及其与管壁的相互作用 为了进一步阐明管道内部颗粒碰撞对管壁磨损的影响规律, 通过分析不同粒径颗粒之间的碰撞以及颗粒与管道壁之间的碰撞分布比例来进行阐述。图8a为不同粒径颗粒间的碰撞及颗粒与壁面的碰撞比例, 对于不同颗粒粒径, 颗粒和管壁的碰撞比例均最大, 颗粒之间的碰撞比例则随粒径减小而减小。这说明颗粒和管壁的相互碰撞是管壁磨损的主要原因, 尤其是大颗粒尺寸和管壁的碰撞。另外, 在浮力和黏性阻力作用下颗粒之间的切向运动导致切向力的出现, 不同颗粒间的相互作用产生的切向力在整个流动过程中的占比如图8b所示: 粒径范围15～30 mm的颗粒与管壁之间的切向作用最为突出, 这说明颗粒粒径越大对管壁的冲蚀磨损作用越明显。图8c为颗粒碰撞导致的能量损失比, 颗粒之间的碰撞会导致能量损失, 且能量损失主要是粒径范围15～30 mm的颗粒与管壁之间的碰撞产生的, 这也说明颗粒粒径越大对管壁碰撞越明显, 对管壁的冲蚀破坏能力也越强, 同时也说明骨料粒径越大越容易堵塞。

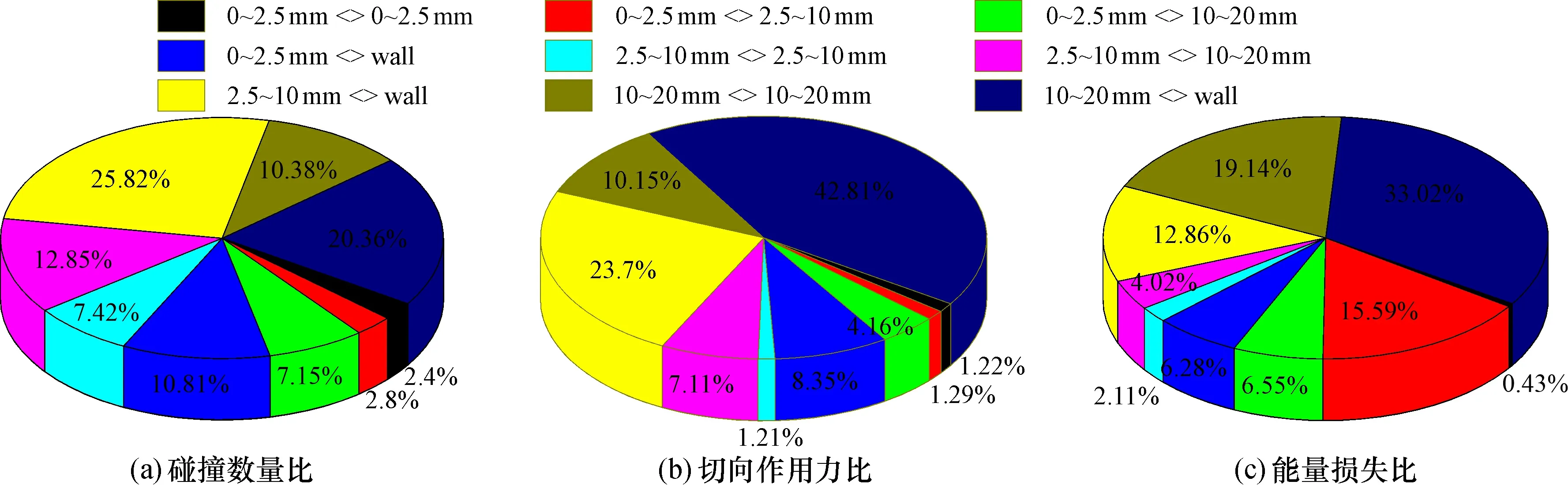
图8 不同粒径颗粒之间及其与管道壁之间的碰撞分布比例

2.5.3 直管段和弯管段比较 通过结合工程实际和模拟结果, 管壁的破损主要发生在弯管处的外凸壁面, 为了揭示其本质规律, 将直管段和弯管段在泵送过程中的碰撞参数进行比较分析。从图9a、 b中可以看到: 混凝土在泵送过程中弯管段的颗粒和管壁的碰撞次数均明显高于直管段, 且弯管段离散固体混凝土颗粒碰撞次数大约是直管段的2倍; 图9c、 d从能量的角度进行了对比分析并发现: 颗粒在直管段的动能明显高于弯管段且弯管段的切向动能损失高于直管段, 这说明弯管段更容易堵塞。

图9 直管段和弯管段颗粒间及其对管壁的碰撞

综上,当颗粒进入管道之后， 颗粒对管壁的碰撞数量逐渐增加,当混凝土充满管道之后就保持稳定状态,并且颗粒在直管段与管壁碰撞数量相对稳定, 而弯管段呈现增加的趋势,同时颗粒在直管段的动能要高于弯管段,颗粒可以快速通过直管段而进入弯管段,由于在直管段停留的时间相对较短,因此在直管段对管道的冲蚀磨损相对较小,在弯管段停留的时间较长增加了颗粒与管壁的作用时间,因此磨损情况要大于直管段,从两个管段的颗粒能量可以清楚地看出， 弯管段的能量损失要远高于直管段。

通过直管段和弯管段内颗粒间的相互作用规律及其对管壁的碰撞机制分析可以发现: 随着时间增加, 混凝土颗粒对管壁的碰撞逐渐增加, 当混凝土充满管道内部达到稳定时, 弯管处的颗粒对管道的碰撞次数开始大于直管处, 直管道的动能要远大于弯管段, 且弯管段的切向动能损失量要比直管段的大, 这是导致管道磨损和疲劳破坏的主要原因。通过混凝土颗粒在管道内直管段和弯管段的动能以及切向能量损失变化规律可以发现: 管道的曲率是影响混凝土泵送过程中堵塞和管道壁面冲蚀磨损的主要原因, 其次是颗粒粒径的大小。

3 疲劳分析与预测

疲劳理论把冲蚀磨损分为变形磨损与切削磨损两部分, 并认为90°冲角下的冲蚀磨损和粒子冲击时靶材的变形有关。在此基础上提出了变形磨损理论, 即材料在反复冲击作用下将产生加工硬化, 提高材料的弹性极限, 当应力超过材料的强度后材料会产生裂纹直至失效。从能量的观点出发, 推导出了总磨损量W和变形磨损量WD和切削磨损量WC之间的关系。

W=WD+WC;

(5)

WD=M(Vsinα-K)2/(2ε);

(6)

(7)

这里,M为冲击磨粒的质量;V为磨粒的速度;α0为冲角;ε为变形磨损系数;Q为切削磨损系数;α0为WC1=WC2时的角度;C、K、K1为常数[20-22]。

疲劳寿命的预测模型主要依据是低周疲劳的曼森(Manson)-柯芬(Coffin)公式

(8)

式中: Δεp为每一循环的平均塑性应变增量;εf为材料断裂时的应变;Nf=(εf/Δεp)2, 为循环次数;Z为材料常数, 这里取0.5。

为了能够有效预测泵送混凝土管道的冲蚀疲劳寿命, 基于断裂力学的低周疲劳原理, 利用DEM-FEA耦合技术及疲劳分析软件NCODE对泵送混凝土管道的冲蚀疲劳寿命进行了模拟研究。选择泵送混凝土充满管道内部并稳定2 s后的流动状态(工况)作为疲劳磨损失效分析及寿命预测的依据, 通过DEM-FEA-NCODE的耦合实现疲劳寿命的预测, 模拟中的材料为龙开口水电实际施工中所使用Q235管道(A283-D), 其疲劳失效云图如图10所示。

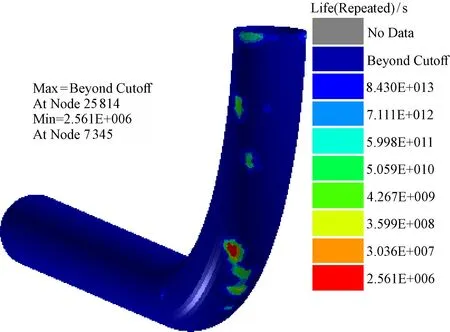
图10 管道在该工况下的磨损疲劳寿命

从泵送混凝土管道受到颗粒冲蚀而产生疲劳失效的疲劳寿命预测结果可见:直管段的寿命远大于弯管段的疲劳寿命;而弯管段则是疲劳失效破坏最易引发磨损失效的部分,且主要发生在颗粒刚从直管段进入弯管的部位,此工况下最严重的位置发生失效的时间是29 d。通过管道失效位置和疲劳寿命的准确预测有利于提前预防、日常维护和更换管道部件,能够减少不必要的事故发生并减小经济损失。

4 结 论

(1)本文使用离散元法和有限元流体动力学DEM-FEA-NCODE模拟了混凝土颗粒对泵送管道内部的冲蚀疲劳过程, 分析了颗粒在管道内部的流动作用机理。 通过研究发现: 粒径15～30 mm的颗粒对管壁的流动冲击和切向力冲蚀作用是导致混凝土管道磨损的最主要因素; 颗粒从直管进入弯管处对外凸管壁的冲蚀磨损最为严重, 结合在整个直管过程中的试验结果(进出口冲蚀相对严重)可以发现， 混凝土在流动过程流场出现较大变化时的位置易产生较大的冲蚀进而引起疲劳失效。

(2)按照龙开口水电站施工的工况, 管内流速1.811 m/s、 内径150 mm的Q235(A283-D)钢管, 对数值模拟与现场施工中的情况进行分析研究可发现: 施工管道寿命为连续施工工况下29 d时间。该模拟结果与龙开口管道冲蚀磨损失效点情况基本一致, 表明离散元与有限元流体动力学以及FEA-NCODE耦合仿真应用在研究泵送混凝土颗粒与管壁相互作用机理方面是可行的。

(3)由于泵送混凝土过程中颗粒对管壁的作用过程在管道内部不易观察, 本文提出 EDEM-FLUENT与DEM-FEA-NCODE耦合仿真运用于泵送混凝土颗粒对管壁作用机理的研究方法, 为泵送混凝土管道寿命预测与失效部位提供理论依据。该方法还能应用于其他流固颗粒耦合作用对管壁冲蚀作业的领域, 由于弯管疲劳失效是主要的导致管道失效的主要原因, 因此对优化改进管道结构进行深入研究。