基于混沌的正余弦果蝇优化算法

张 伟， 张 亚

(安徽理工大学 电气与信息工程学院， 安徽 淮南 232001)

果蝇优化算法(Fruit Fly Optimization Algorithm，FOA)是模拟果蝇寻找食物这一过程的优化算法，和同类算法相比，具有结构简单、参数少等优点，被应用于解决诸多实际问题[1,2]。文献[3]将FOA和支持向量机以及季节指数调整相结合构造模型，用来预测月度旅游流量，为更好的旅游规划和管理提供可靠指导。文献[4]提出一种基于FOA的随机森林预测方法，利用FOA对随机森林的参数进行优化，构造随机森林模型。文献[5]利用FOA对多目标函数寻优以获得电流的最佳参考值，实现对联网逆变器的协调控制，提高非均衡电网中联网逆变器的整体控制性能。文献[6]将FOA与局部搜索相结合寻找复杂物流网络中有容量限制的多车厢车辆的最优路径，提高物流配送的效率，降低运营成本。

由于算法本身特点，在迭代时容易发生早熟现象，在解决高维数学和实际应用问题时难以达到预期效果。因此，诸多研究人员对标准FOA进行改进。文献[7]将该算法的迭代步长值作为设计自适应搜索的指导因素，协调全局和局部搜索。在算法后期，基于正态云提出了云逃逸机制，帮助算法更好地逃离局部最优。文献[8]使用蝙蝠声纳策略搜索全局最优值，将高斯分布和生分布组成的混合分布机制用于搜索全局最优的局部区域。结果表明所采用方法在解决连续和离散优化问题方面的优越性。文献[9]提出将果蝇的搜索空间由二维空间改为三维空间，扩大搜索范围。将固定的步长更改为线性减小的步长，以避免被困在局部最优值中，从而提高寻找食物的精度。然后，以改进的FOA和广义回归神经网络为基础建立模型，进行灾害预测。文献[10]将高斯变异算子引入基本FOA以避免过早收敛，采用混沌局部搜索方法，提高了种群的局部开发能力，然后将其应用于特征选择问题。

上述改进的果蝇算法，解决了一些特定问题，但仍存在收敛速度慢和陷入局部最优的问题。因此，本文提出一种基于混沌的正余弦果蝇优化算法(chaos-based sine-cosine fruit fly optimization algorithm，CSC-FOA)。首先，混沌初始化种群的位置，利用混沌变量的遍历性，使初始的果蝇个体处于最优值附近。其次，引入正余弦搜索策略使果蝇向外或向最优解飞去，以避免陷入局部最优，提高算法收敛速度。

1 改进的果蝇优化算法

果蝇普遍分布于温热带气候中，拥有极佳的嗅觉和视觉。在觅食时，果蝇先通过嗅觉判断食物大致方位，然后用视觉确定食物所在的具体位置[1]。

1.1 混沌初始化种群

作为启发式算法的一种，FOA的性能受种群初值的影响较大。若初始化种群的位置靠近最优值，则有利于算法的收敛速度加快，精度提高。然而FOA随机产生的果蝇种群位置一般并不理想，远离最优值，降低算法后期的寻优速度。混沌是一种常见非线性现象，混沌变量具有随机性、规律性以及遍历性的特点。因此，本文采用logistic映射以改善随机初始种群对FOA性能的影响。k为当前迭代次数，Cxi为混沌变量，其迭代公式如下：

Cx(k+1)i=uCx(k)i(1-Cx(k)i)

(1)

式中，u为控制参数。如果所求问题变量满足xi∈[σi,φi],σi,φi分别表示该变量取值范围的下限与上限，那么该变量可通过式(2)和式(3)混沌变量的逆映射得到。本文通过变量间的映射关系，使果蝇位置均匀地分布于解空间，然后带入目标函数计算，选择其中最优值作为初始种群位置。

Cxi=(xi-σi)/(φi-σi)

(2)

xi=σi+Cxi(φi-σi)

(3)

1.2 正余弦果蝇优化算法

正弦余弦算法[11]是近几年提出的一种优化算法，首先随机产生多个候选解，在探索和开发阶段，通过随机选择正弦或余弦更新位置信息，使它们向最优解振荡或向外飞去。大量研究表明，这种波动搜索方法不仅可以提高收敛速度，而且可以避免候选解落入局部最优值。正弦余弦算法的个体位置更新公式如下：

(4)

(5)

式中：(Xijg，Yijg)表示第g次迭代第i个果蝇在第j维的位置；(X_axisg，Y_axisg)表示当代最优位置；r1表示控制搜索方向，也是当前解迭代所能达到的步长极值，其公式如式(6)所示。r2，r3，r4为3个服从均匀分布的随机数：r2表示向当前最优果蝇靠近或远离的程度；r3描述了果蝇受当前最优果蝇影响程度；r4决定了算法进行正弦搜索还是余弦搜索。

(6)

式中：a为常数，g为迭代数，maxgen为最大迭代数。

在FOA中，果蝇采用随机策略更新位置，然后根据果蝇位置计算味道浓度判定值，以获得候选解。随机策略在平衡全局搜索和局部开发方面发挥着重要作用。而随机策略中果蝇位置的更新受最优果蝇位置以及步长的影响，导致算法容易陷入局部最优，影响收敛速度。针对随机策略的缺点和正弦余弦策略的优点，本文提出使用正弦余弦策略而不是随机生成的方向和距离来提高收敛速度，解决局部最优停滞的问题。

为了使算法更好地兼顾算法全局搜索和局部开发，对正余弦搜索策略加以改进。其中参数r1的变化对搜索策略的性能有重要影响。因此，通过非线性的方式调整r1，先加强全局搜索，然后逐步向局部开发过渡，加快迭代后期的非线性递减以加强局部开发。调整后的表达式如下所示。

(7)

2 实验及结果分析

2.1 实验设计

为了验证CSC-FOA的可行性，以求解函数最小值为目标进行实验。实验选用6个单、多峰函数，其中f1、f5为2个单峰函数，f6为2维函数，其余为多维函数。测试函数的各项参数信息如表1所示。实验参数设置为：种群数sizepop=30，最大的迭代数maxgen=200。

评估算法性能优劣采取的方法：(1)固定迭代次数，评估算法的寻优能力和稳定性，并与粒子群算法以及文献[12]的SHFOA进行比较。各算法参数设置为：PSO的参数c1=c2=1.5，w=0.8；FOA的参数RandomValue∈(-10,10)；SHFOA的参数Wstart=1.5，Wend=0.1；CSC-FOA的参数a=2。(2)评估算法在多峰，高维函数的寻优性能。

表1 测试函数

2.2 实验结果和分析

2.2.1 固定迭代次数，算法的收敛速度和精度

固定算法迭代次数200次，将FOA、PSO、SHFOA和CSCFOA算法分别对函数寻优，所得结果的均值和标准差作为评价算法优劣的指标。为了避免单次实验的偶然性导致对算法性能的错误认识，对每个函数进行20次连续独立实验，实验所得结果的平均值如表2所示。

从表中可以看出，对于多峰函数，CSC-FOA的优化性能优于其他算法。其中，Griewank函数的极小值点无数，而只有x=0时，函数取得最小值，故在算法寻优时很难找到其全局最优。Schaffer函数为2维多峰函数，4种算法寻优结果较佳，且优于对单峰函数的寻优结果。对单峰函数Sphere和Rosenbrock，CSC-FOA的均值和标准差均优于其他算法。其中，Rosenbrock函数的寻优效果不明显，与其他算法处于同一数量级。Rosenbrock函数也称山谷函数，其最小值位于值域变化不大的山谷中，导致CSC-FOA的优势表现不明显。虽然CSC-FOA对不同测试函数的寻优性能各不相同，但对同一个测试函数，无论是单峰还是多峰，CSC-FOA的寻优性能强于FOA、PSO和SHFOA。

表2 算法优化性能比较

续表2

为了更加直观地比较和分析算法对函数的寻优效果，图1～图6为相同迭代次数下各函数的适应度曲线(为便于观察，除Rosenbrock函数，其余函数适应度取以10为底的对数)。从多峰函数的进化曲线中可以看出，与FOA、PSO、SHFOA相比，CSC-FOA无论是速度还是精度均有明显提升。尤其是Griewank函数、Rastrigin函数和Schaffer函数，效果更为明显且寻优结果接近最优值。对于单峰函数，CSC-FOA也能快速收敛，尤其是Rosenbrock函数虽寻优结果欠佳，但相比其他3种算法，收敛速度有明显提升。总体而言，CSC-FOA算法具有更好的优化性能。

图1 Sphere函数适应度进化曲线 图2 Griewank函数适应度进化曲线

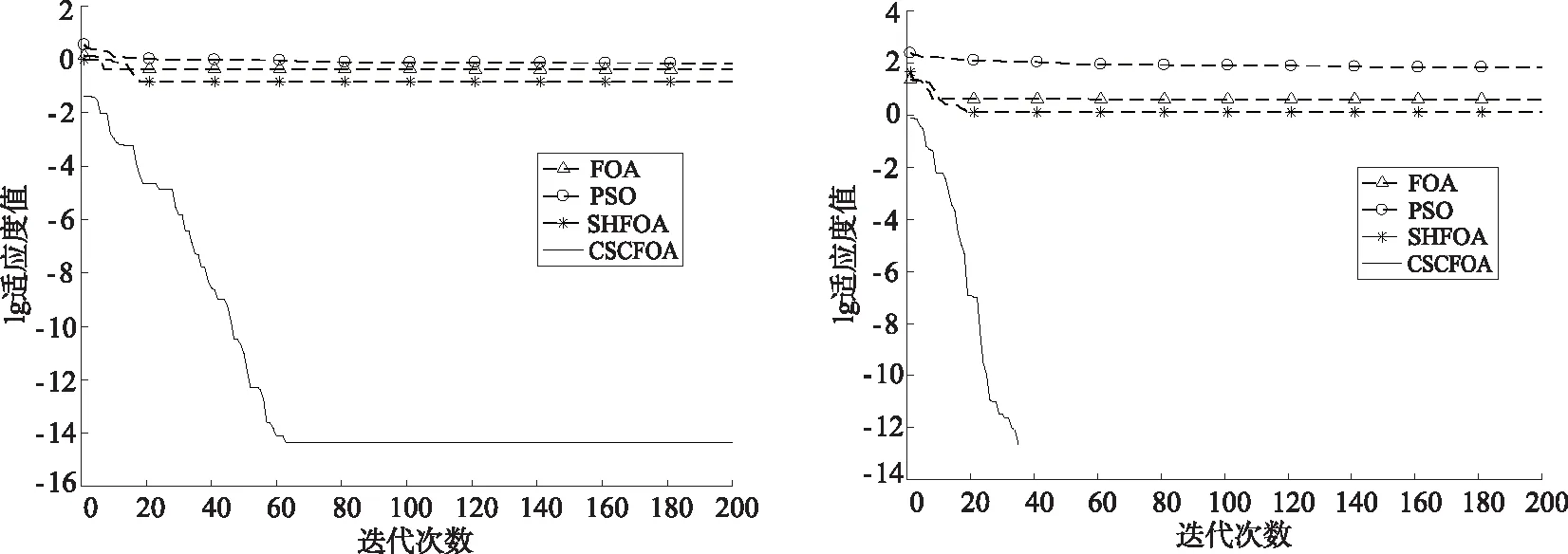
图3 Ackley函数适应度进化曲线 图4 Rastrigin函数适应度进化曲线

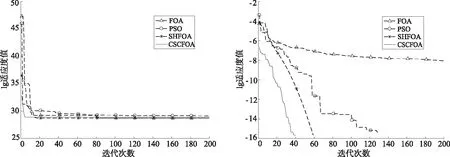
图5 Rosenbrock函数适应度进化曲线 图6 Schaffer函数适应度进化曲线

2.2.2 算法在多峰、高维函数的性能测试

为了验证CSC-FOA算法对高维、多峰函数的寻优依旧具有优势，在3个多峰函数的维度依次递增情况下，对CSC-FOA算法和FOA算法优化结果进行比较。种群大小为sizepop=30，最大迭代数为maxgen=200，算法参数保持不变，连续运行20次。函数的维度从30维递增至120维。测试结果如表3所示。

表3 算法在不同维度的性能比较

从表中可以看出，随着测试函数维度的增加，算法的寻优性能都有所下降，但CSCFOA的下降幅度较低，保持在同一数量级。对于同一函数，CSCFOA在高维度的寻优结果远低于FOA低维度的结果。通过结果对比，我们可以发现CSCFOA在多峰、高维函数的寻优上依旧保持较快的收敛速度和较高的收敛精度，进一步说明了本文采用改进策略的可行性。

3 结 语

在保持果蝇优化算法良好性能的基础上，提出了基于混沌的正余弦果蝇优化算法。将混沌变量的遍历性特点应用于初始化果蝇种群位置，降低随机初始化对果蝇算法性能的影响。采用正余弦搜索策略更新果蝇位置而不是随机搜索策略，提高算法寻优速度和逃离局部最优。通过对6个函数的寻优实验，结果表明，本文提出的CSC-FOA有效地提升了寻优精度和收敛速度，验证本文改进的算法在实际问题中的可行性是下一步研究的重点。