时间敏感网络中基于网络演算的队列分析与优化
2022-04-05尹淑文汪硕黄韬
尹淑文 汪硕 黄韬






摘要:時间敏感网络(TSN)中循环队列转发(CQF)机制保留了时间感知整形中门控调度的转发可控特性,同时又降低了门控列表配置的复杂度,但是缓存队列的长度作为一个关键参数直接影响着网络的调度性能,并且在实现时受到硬件资源的约束。为了寻找到合适的 CQF 队列长度值以实现网络系统设计的性能和成本的优化,提出了一个基于网络演算的 CQF 性能分析方法。通过曲线模型的构建和计算,分析流量传输时延和积压的性能上界值,从而选择出合适的队列长度值。通过不同场景的实验,得到了不同流特性参数对队列长度选择的影响。
关键词:时间敏感网络;循环队列转发;网络演算;性能分析;队列长度分析
Abstract: Cyclic queue forwarding (CQF) in time-sensitive networking (TSN) remains the forwarding controllability based on gated scheduling in time-aware shaper and reduces the complexity of the configuration of gate control lists . However, as a key parameter, the length of CQF queues directly affects the performance of network scheduling and is constrained by hardware resources in implementation . In order to find the appropriate value of CQF queue length to realize the performance and cost optimization of network system design , a performance analy⁃ sis method of CQF-based networks based on network calculus is proposed . Through the construction of curve model and calculation, the upper bounds of delay and backlog of data traffic transmission are analyzed . Then the appropriate length of CQF queues can be selected ac⁃ cording to these analysis results . Experiments are conducted in different scenarios, and the influence of different flow characteristic param⁃eters on the selection of queue length is obtained .
Keywords: time-sensitive networking; cyclic queue forwarding; network calculus; performance analysis; queue length analysis
由于越来越多的应用,如工业控制、自动驾驶、实时交互、远程医疗等,对网络端到端传输提出有界低时延的需求,以时间敏感网络(TSN)作为标准的、开放的链路层确定性技术受到了广泛关注[1]。
TSN 引入了调度整形机制为时间敏感流量在路径上传输提供确定的传输时隙。其中,基于时钟同步的时间感知整形(TAS)机制[2]通过控制出端口队列上的门开关状态来实现对流量的精确转发控制,是 TSN 中广泛使用的整形机制。然而,这一机制需要通过复杂的计算为每一个出端口的每一个队列分配一个门控列表。为了简化配置问题, TSN 工作组在标准中提出了循环队列转发(CQF) [3],即一个队列接收数据,一个队列转发缓存数据,两队列采用周期性交替的方式进行传输。
目前, CQF 的相关研究目标是实现基于该机制的端到端传输。例如,通过一系列约束条件规划出每条流从终端设备发包的时间,以实现无冲突的有界低时延传输。其中,队列长度仅作为资源约束中一个固定数值参与调度时间规划的计算[4-5]。然而,端口队列长度也对基于 CQF 机制的网络传输性能产生重要的影响,并与实现难度和成本相关。分析队列长度的选择是基于 CQF 机制进行交换机设计的重要内容,但当前仍缺乏这类研究。
网络演算作为一种网络性能分析的理论工具,根据流的特性刻画到达曲线以构造数据流量模型,同时根据网络节点转发服务能力刻画服务曲线以构造节点服务模型,提供了一个从理论上进行网络性能分析的工具[6]。因此,网络演算在 TSN 领域也得到了关注和应用,如为音视频桥接(AVB)流传输建模提供性能分析和传输保障[7-8];构造基于传输窗口的模型,并实现 TAS 机制性能分析和门控列表配置验证等[9]。上述这些研究通常集中在整形机制的时延边界分析方面,很少关注流量积压边界的问题。
针对 TSN 中的 CQF 机制,本文提出了一种基于网络演算的队列分析优化方法。该方法首先建立了一个基于 CQF 的网络系统的性能分析模型,再利用该模型对节点内积压和流量端到端时延进行分析并选择出合适的队列长度值。这一方法能够在理论上整体分析流量在节点上的流量积压边界,不受单条流调度规划的限制,避免了多次约束求解所造成的时间和资源浪费。
1研究背景与动机
1.1 CQF机制
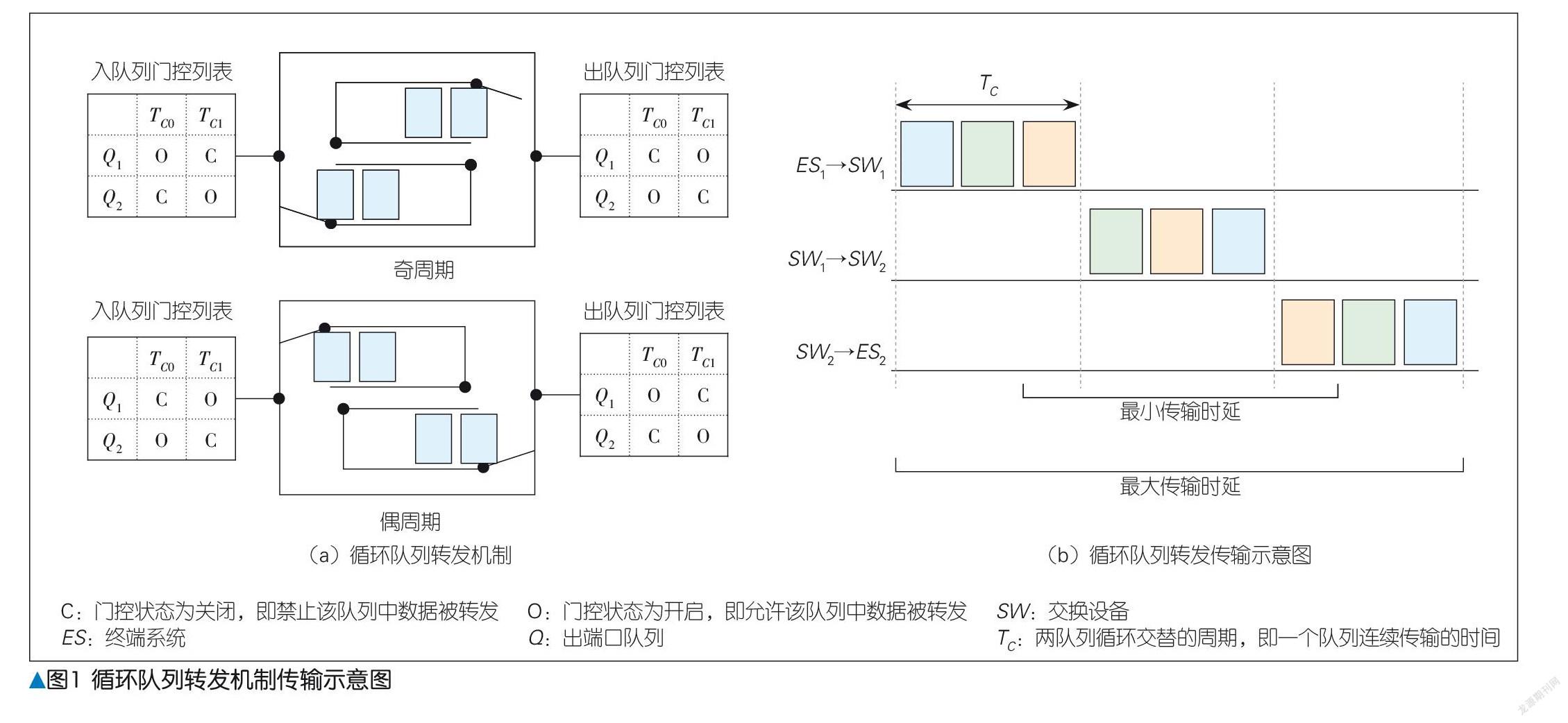
CQF 机制沿用 TAS 机制的门控方法,当门开启时,队列中的数据被允许转发到下一节点;当门关闭时,进入到队列的数据将被缓存在队列中以等待传输。然而, CQF 利用静态门控,并采用两个队列周期交替去取代 TAS 中一个门控队列的功能,如图1 (a)所示。在 CQF 的奇数循环中,缓存到奇队列中的数据被转发到下一节点,到达该交换机端口的数据则进入到偶队列中;在 CQF 的偶数循环中,情况则与之相反,即奇队列进行缓存,偶队列进行转发。
数据帧在路径节点上的转发传输过程如图1 (b)所示。假设 CQF 的循环周期,即两队列交替的时间间隔为 TC,流端到端传输路径的总跳数为 H,则传输的最小时延Dmin =H -1× TC,传输最大时延为Dmax =H +1× TC。
1.2网络演算理论基础
网络演算以最小加代数为理论工具[10]。其中,最小加代数中的卷积运算如公式(1)所示,最小加反卷积如公式(2)所示[6]:
到达曲线通常描述的是到达节点流累积量的上界,为广义增函数。假设累积到达流Rt的到达曲线为α t,则它们的关系如公式(3)所示:
服务曲线通常用来描述节点累计服务量的下界,也是一个广义增函数。假设流量被节点服务后离开的累积量为 R*t,节点的服务曲线为βt,则其关系如公式(4)所示:
根据上述所定义的模型,我们可以得到流在该节点的排队时延和該队列的流量积压边界,并进行性能分析。对于一个无损的先入先出系统,在 t时刻输入数据的时延上界如式(5)所示,输入数据在该节点的流量积压如式(6)所示。
由于到达曲线和服务曲线表示最差情况下的节点传输状
态,因此流在节点的传输时延上边界为两条曲线的最大水平距离,即 Hα, β,如公式(7)所示。流量积压上边界为两曲线最大垂直距离,即Vα, β,如公式(8)所示:
对于需要控制数据输出的设备或机制,网络演算定义了整形器的概念。整形器具有一条整形曲线σ t。整形器的输出需要遵守该整形曲线,以曲线所定义的输出量为上界。其中,能够将输入数据存放在缓存中,并在满足整形曲线时尽快把数据转发的整形器被称为贪婪整形器。
1.3队列长度的影响
在进行交换机设计或对拓扑抽象建模时,队列长度都是一个重要的设计参数。在进行流量调度规划时,假设基于 TAS 机制的网络模型的端口队列长度足够使用,不会出现丢包的情况[11],流在调度约束中不会受到队列资源的限制。然而,在 CQF 网络中,队列长度与传输时隙的大小有直接关系。一个传输时隙需要保证 CQF 队列中的所有数据包一跳转发。因此,流传输需要受到队列资源的约束。
实验表明, CQF 队列长度的减小能够使其所能容纳的包数量减少,在合理范围内算法的可调度流数量也会随之减小[5]。当 CQF 队列长度过小时,虽然流量传输的单跳排队时延很小,但是交换机端口内没有足够的空间去缓存更多到达流。如果网络系统中存在发包周期不同的流,就需要对流的发包时间范围进行严格限制,以避免在传输中出现内存溢出导致丢包的现象。这将限制终端设备的发包数量和种类,从而限制网络系统可调度流的数量。
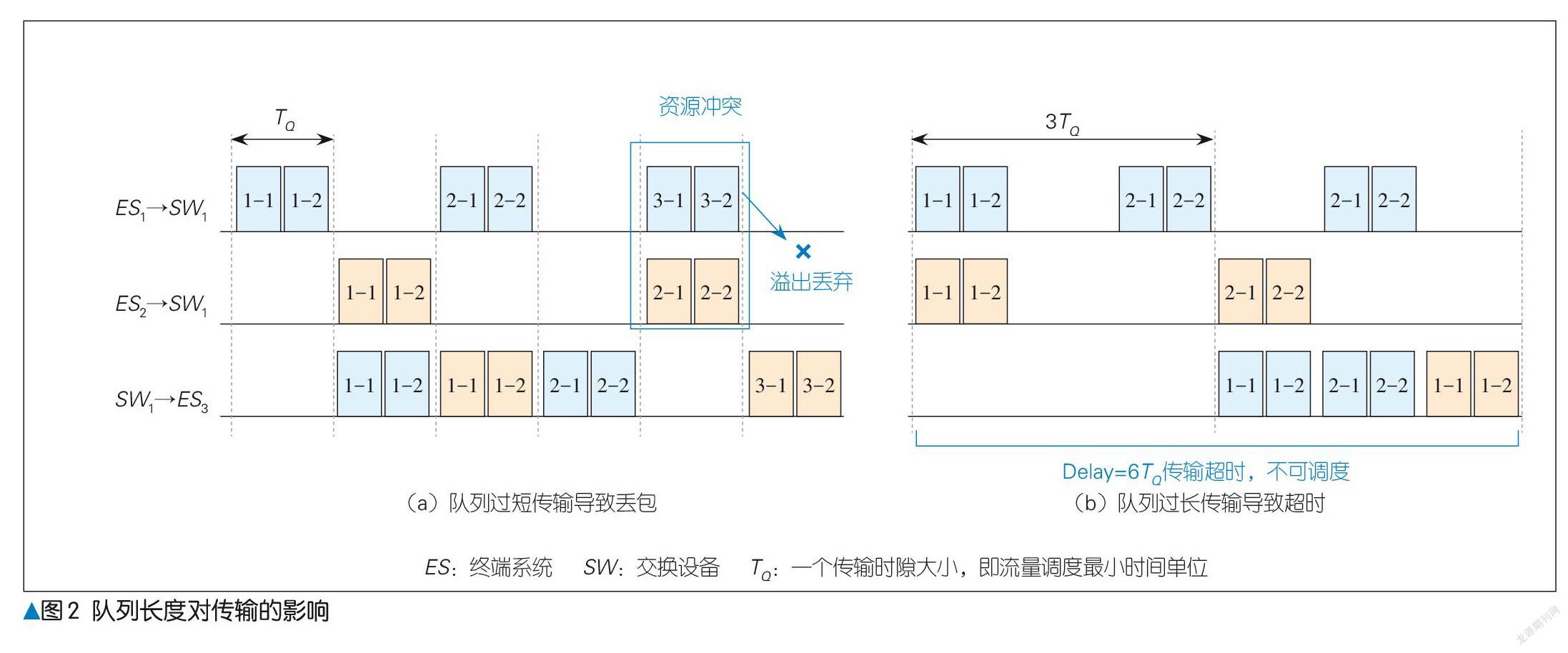
以图2 为例,把3 个终端设备连接到1 台交换机上组成一个简单拓扑。当流f1从 ES1发送到 ES3时,周期为2TQ,并且一次发两个包;当流f2从 ES2发送到 ES3时,周期为3TQ。 f1和f2可容忍的最大时延都为5TQ 。两条流在传输时都将经过交换机 SW1连接 ES3的端口,在调度规划时需要避免队列溢出丢包的情况。当 CQF 两个队列功能切换的交替周期 TC 为 TQ 时,队列长度可容纳两个最大传输单元大小的包。然而,由于流f1和f2的发包周期互为质数,在调度的超周期(两周期的最小公倍数)内系统无法实现无溢出的调度规划,
如图2 (a)所示。因此,数据包一定会因为队列资源不足而溢出,进而造成丢包。
当 CQF 队列过长时,流传输的单条排队时延会同样变得过大。这就使流的端到端传输时延过长,从而可能导致流的不可调度,造成网络系统的可调度性能变差。同样以图2 为例,网络和流特性参数同上,在图2 (b)中 CQF 两队列交替周期 TC 为3TQ 。根据该机制包传输时延计算,其时延最大可达到6TQ 。可以看出,该时延边界超出了流可容忍时延的范围。
此外,由于底层硬件资源有限,内存越大其实现的难度和成本也就越高。因此,队列长度在满足传输需求的同时应尽可能地小,以减少所需资源。
队列长度作为流量调度时的一个资源约束条件的同时,也对流量调度结果有着重要的影响。基于 CQF 机制的调度算法设计的重点在于对流发包时间的规划。将时间敏感流量映射到基于 TSN 的底层硬件资源上时,队列长度被赋予一个固定值来调度并进行约束[4]。目前,有关队列长度对调度影响的研究[5]还比较少,对于队列长度如何进行选择的研究更是缺乏。因此,我们需要一种能够根据场景进行队列分析优化的方法。
2模型与分析
2.1模型概述
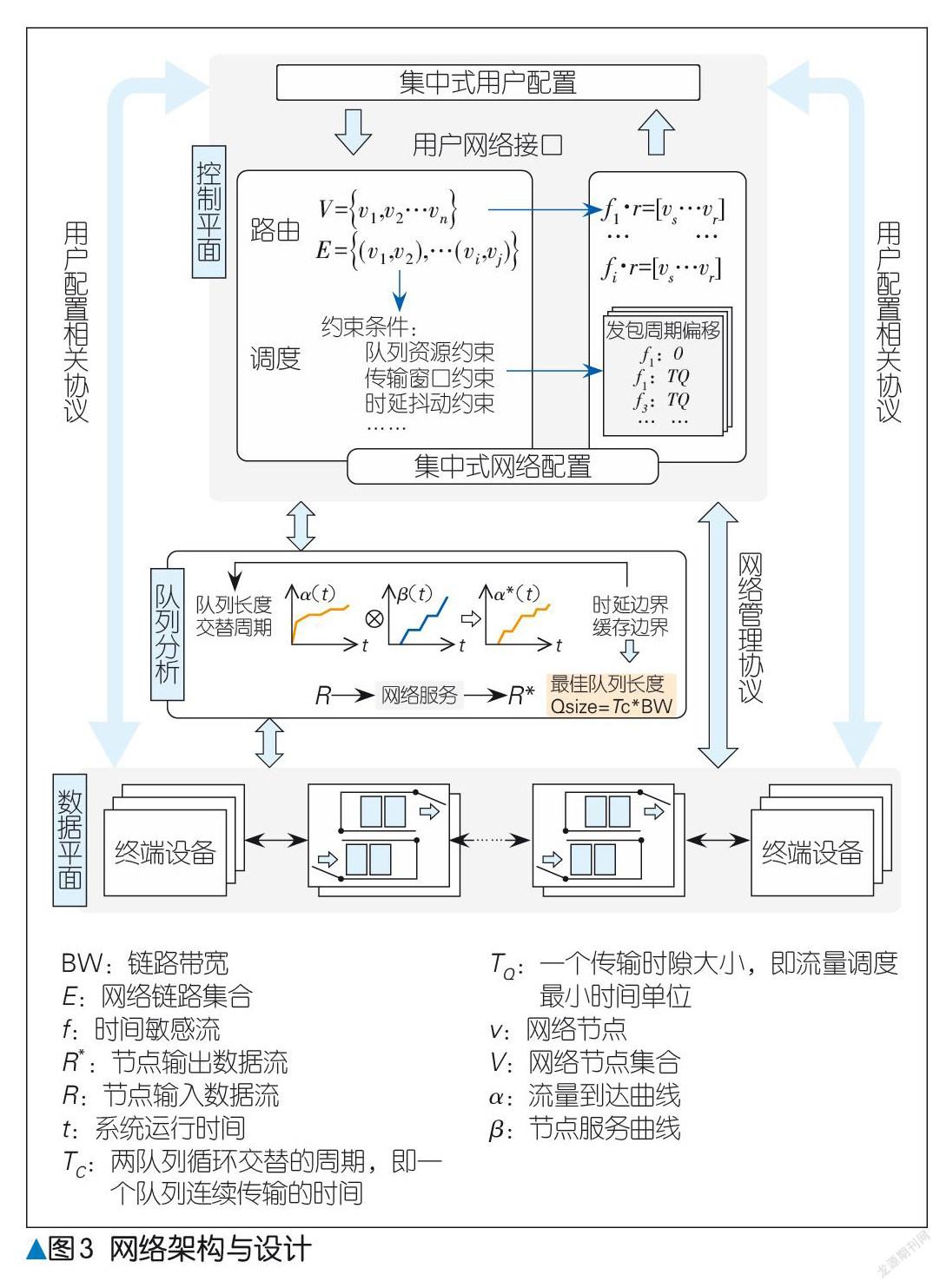
根据 IEEE 802.1 Qcc(电气与电子工程师协会标准)所提出的集中式控制架构,基于 CQF 的 TSN 网络架构可以分为数据面和控制面两个部分,如图3 所示。数据面的拓扑、设备和流特性抽象为一个全局的资源视图,并作为控制面的输入数据。控制面采用设计的调度算法,根据输入进行调度计算,并下发给数据面设备。随后,数据面设备根据收到的配置信息来控制数据包的发送。
在从数据面信息抽象时,设备的队列长度将作为一个既定的信息参数图输入至控制面。在控制面中,调度器利用一个确定的队列长度值来进行资源约束。本文所提出的分析方法应用在整个网络架构之外,如图3 所示。在理论层面,该方法利用 TSN 网络抽象模型中数据面的全局资源信息和控制面路由结果,分析出最佳队列长度参数,并将该参数反馈至数据面,调节网络模型的队列长度,为可编程交换机参数设置[12]或者 TSN 交换机设计和型号选择提供参考。
该方法不仅能根据当前场景的终端设备和流量特性构造出数据流量模型,还可根据交换机信息构造队列服务模型,基于网络演算理论计算流量端到端传输性能参数,并反馈调节队列参数,最终可得到最佳队列长度值。
2.2队列服务模型
CQF 机制利用两个相同的队列进行乒乓交替传输。从节点传输上来看,该端口节点始终为线速转发。然而,在数据传输方面,数据帧先进入端口的一个队列等待,再以线速传输转发。在对端口节点进行服务模型分析时,从单独 CQF 队列出发,我们把 CQF 服务模型分为奇队列和偶队列两个部分。其中,奇队列在奇数交替周期转发,偶队列在偶数周期进行转发。
根据网络演算理论, CQF 服务队列可建模为贪婪整形器[6]。在整形曲线σ t满足次加性并且初始时值为0 的情况下,缓冲区初始状态为空且足够大的贪婪整形器的输入输出特性满足公式(9),即节点为流提供了一条等于σ 的服务曲线。
为了获得更细粒度的 CQF 队列服务模型,整形曲线的构造可根据时分多址(TDMA)总线协议的经典服务模型[13] 来完成,进而分阶段描述出转发服务和缓存等待两个过程。在转发服务阶段,整形曲线以交换机传输速率为斜率递增;在缓存等待阶段,整形曲线累积服务量不随时间的增加而变化。根据两队列工作机制,奇队列在一个调度超周期初始时刻即开始进行转发,其整形曲线表达如公式(10)所示。偶队列等同于在奇队列前再加入一个恒定突发延迟函数δT。该函数的值在 t ≤0 时为0,其他情况为∞ 。偶队列整形曲线表达满足公式(11)。其中, TQ 为队列转发的交替周期, C为端口转发速率。
2.3数据流量模型
在构造数据流量模型时,模型仅对流特性已知,对流量发包时间的调度未知。因此,流量到达曲线的构造以经典的漏桶模型为基础,相关定义为α (t)= b + rt 。对于终端设备输出数据量曲线,参数恒定速率 r和瞬时突发 b可以根据流的发包周期f.period、数据包大小f.size和一次发包数量f.num求出。一台终端设备累积输出数据量上界的曲线参数 r和 b 的计算公式如(12)和(13)所示:
基于上述漏桶曲线,根据 CQF 机制工作模式得到终端设备在奇偶周期流量发送曲线。下一节点的偶队列的到达曲线,即终端设备在奇周期的累积输出数据量α oddt如公式(14)所示;奇队列的到达曲线,即终端设备在偶周期的累积发送数据量α even t为α oddt延迟一个交替周期 T后的结果,如公式(15)所示。
2.4性能与参数分析
流从发送端输出后将根据传输路径经过多个串联的网络节点,然后到达接收端。根据串联等效定理[10],这些串联的节点为一条流所提供的服务量可以使用一个服务模型来代替。假设这些串联节点提供的服务曲线依次为 β1 t, β2t, …,βn (t),则该串联等效模型服务曲线为β (t)= β1 ⊗β2… ⊗βn (t)。
当时间敏感流在基于 CQF 的网络系统中传输时,缓存在奇队列中的数据将转发至偶队列中,同时偶队列中的数据将转发至奇队列中。根据 CQF 传输时延边界公式、串联等效定理和贪婪整形器输入输出特性,奇数周期从发送端输出的到达曲线为 α odd(t)的数据流 Rodd(t)。在经过路径节点 v0,v 1, …,vn的服务后,接收端所接收到的输出数据流 Ro(*)ddt满足公式(16)。同理,偶数周期发送流的输出 R e(*)vent满足公式(17)。
根据传输时延公式, CQF 的网络系统中到达曲线为α t数据流的端到端传输时延边界,如公式(18)所示:
根据剩余服务定理[10],当多条流同时到达同一网络节点并竞争使用该节点提供的服务时,假设这些流的到达曲线分别为α 1,α2, …,α n,节点提供给所有流的总服务曲线为β (t),则节点提供给到达曲线α n 的数据流的服务曲线为βn (t)= max(0, β- α1 -α 2… -α n -1)。
在 CQF 机制下,流量到达队列先缓存后进行转发。相对于流到达, CQF 队列对流服务有一个周期的延迟。节点的剩余服务为 β n (t)= max(0, β- α1 ⊗δ T - α2 ⊗δ T …- α n -1 ⊗δ T )。在进行性能分析时,系统按照最大可容忍时延从小到大的顺序对流进行逐一端到端传输分析,并沿路由更新交换机端口剩余服务曲线,以用于下一条到达流量服务分析。端口剩余服务曲线不足以服务的流则滞留在该端口队列中。根据流量积压公式,端口队列中流量积压量如公式(19)所示:
Backlog (t)= R (t)- R*(t)≤ [ αi (t)- α i⊗ βi (t)] 。(19)
如图3 中队列分析部分所示,在利用上述分析模型进行队列参数的选择时,首先将队列长度的初始状态设置为一个最大传输单元,再构建该系统的流量和服務模型,以便得到流量端到端传输时延和各个端口的流量积压值。
当队列过小时,队列长度不足以容纳端口流量积压量,数据包将被丢弃。此时,系统会根据当前队列长度和流量积压参数将队列长度调大,队列长度增量值如公式(20)所示。其中,Backlogmax为超周期内所有队列流量积压量的最大值,AdjustNum参数控制节幅度随着调节次数的增加而减
小,队列长度调节单位为最大传输单元1 500 B。
∆Qsize = max1, /AdjustNum×1500。(20)
当队列过大时,传输时延不满足可容忍最大时延约束条件。此时系统会根据当前时延和流的可容忍最大时延差值将队列长度调小,直至传输时延和队列缓存都满足相关条件,相关计算如公式(21)所示。其中,Delayi为流fi 性能分析得到的传输时延,delayi为流fi 最大可容忍传输时延, Hopi为流fi 跳数。
∆Qsize = max 1, max ( ) / AdjustNum×1500。(21)
随后,系统会返回该理想的队列长度值并将其作为最佳队列长度参数,或者达到最大调节次数后退出。如果选择失败,则说明当前场景无法选择出理想的队列长度值。
3实验与结果
3.1实验设置
3.1.1 网络拓扑
本文实验所采用的拓扑为常用于工业控制网络的线性拓扑和环形拓扑,如图4 所示。线性拓扑的流量数据在交换机节点中可以双向传输,环形拓扑的流量数据在交换机节点之间只能沿着一个方向进行传输。
由于队列分析方法的应用不受网络规模限制,实验时线性和环形拓扑中的交换机数量固定为10个,网络带宽都设置为1 Gbit/s 。 CQF 队列长度初始值被设置为一个最大传输单元1 500 B,系统以1 500 B 的幅度进行调节,以保证数据传输的完整性。实验在 Intel(R) Core(TM) i7-6700 RAM 16GB 的 Windows 设备上,基于 Python 开发的分析系统进行测试。
3.1.2 流量特性
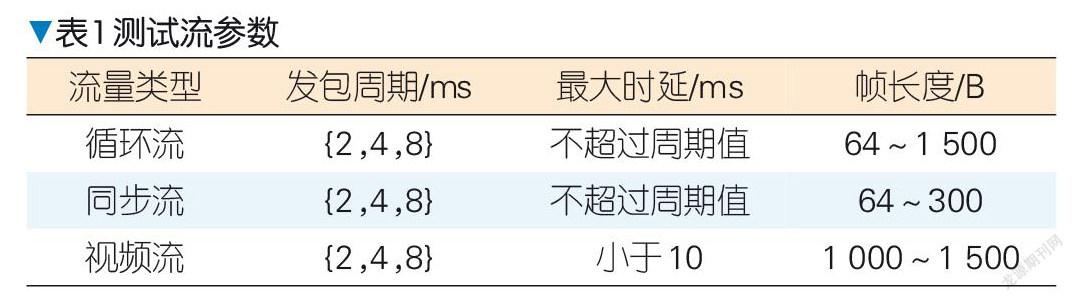
由于没有可以直接应用于实验测试的标准 TSN 流量集,本实验参考国际电工委员会(IEC) /IEEE 60802标准[14]中描述的工业自动化网络流量特性进行参数设置,从不连接同一交换机的终端设备中随机选取一组作为流的发送和接收设备,并采用最短路径计算出相应的传输路径。流的发包周期以毫秒为单位,并且该发包周期从集合{2, 4, 8} ms中选取。流的最大可容忍时延一般为时延系数集合中随机选取的一个系数与其发包周期的乘积,流的一个数据帧长度范围为64~1 500 B。
在该实验中,时间敏感流量类型主要分为循环流、同步流和视频流3 种[15],相关参数如表1 所示。循环流主要用于设备之间的周期性通信,它的可容忍最大时延与发包周期相关,一般不超过其周期值。同步流主要用于控制器或设备之间的同步交互,它的最大时延通常在一个周期以内,数据帧通常很小。视频流是终端直接传输的视频数据流,面向用户的视频流的性能相对较低,其特征是延迟小于10 ms,以保障用户体验。视频流的帧长度一般为1 000~1 500 B 。根据码率可以近似得到等价发包周期。
3.2实验结果
实验分别分析了流特性中的发包周期、最大可容忍时间和网络拓扑类型对队列分析结果的影响,并对具有明显差异的同步流和视频流进行队列分析,将其作为队列分析场景应用示例。
3.2.1 发包周期
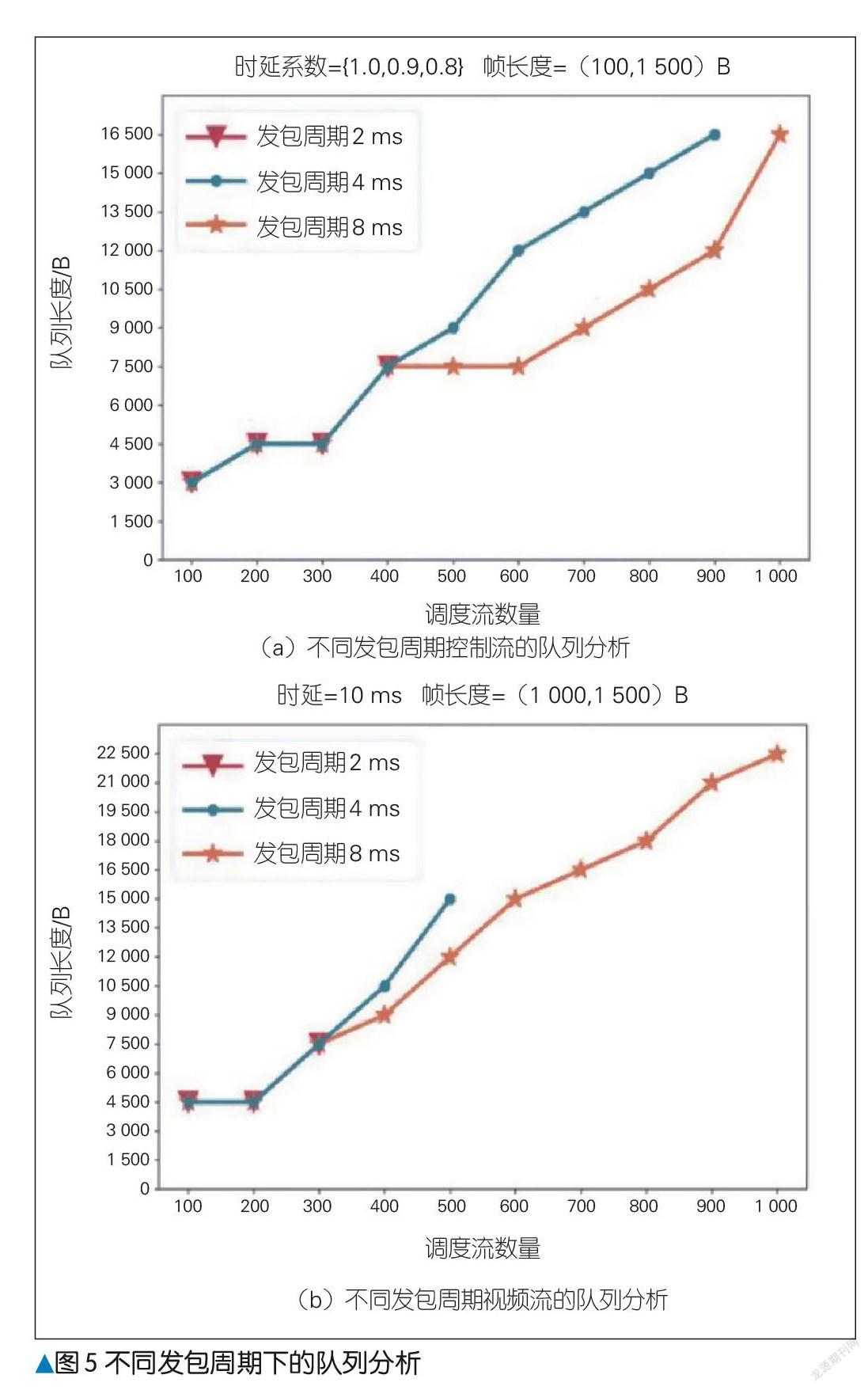
在不同发包周期下进行队列分析的实验中,测试采用线性拓扑并分别采用具有固定时延系数的循环流和固定时延的视频流,测试结果分别如图5 (a)和图5 (b)所示。随着发包间隔的增大,流从终端设备注入的时间有更大的选择范围,流量更加不易聚集,因此可调度的流数量随之增加。随着调度流数量的增加,发包周期大的流所需要的队列长度逐渐小于发包周期小的流量。
3.2.2 最大时延
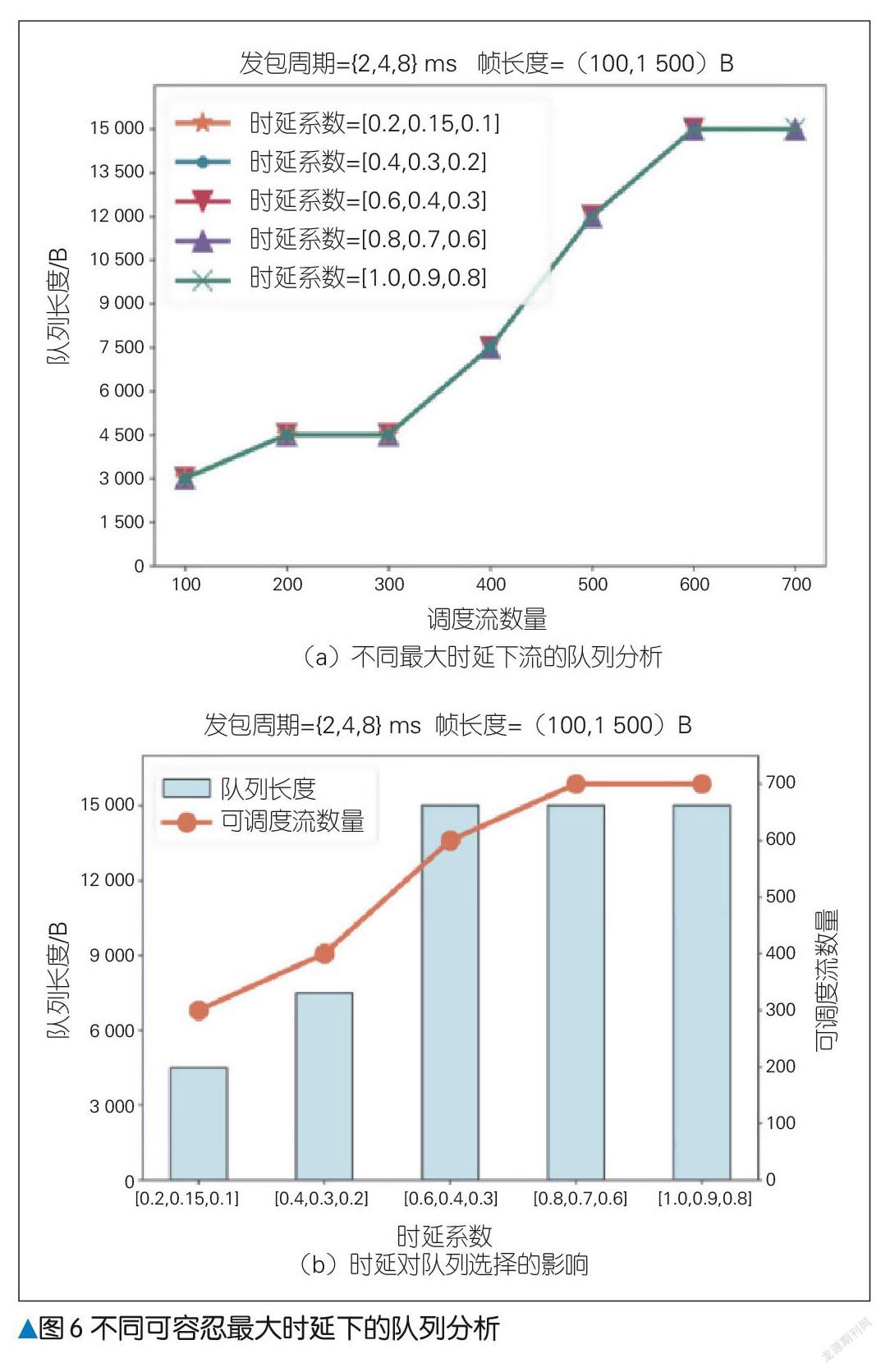
在不同可容忍最大时延下进行队列分析的实验中,测试采用线性拓扑和具有不同时延系数的循环流。该循环流单条流的周期从周期集合为{2, 4, 8} ms中进行选取,帧长度从100~1 500 B 中选取。实验采用5 组时延系数进行分析,实验结果如图6 所示。从图6 (a)中不同组队列长度曲线重合可知,在可调度流数量范围内,流的可容忍最大时延并不影响队列长度的选择;然而,流可容忍最大时延会影响队列选择范围和与之对应的流的最大可调度数量,即随着可容忍最大时延的增大,可选择队列长度会增大,可调度流数量也会增多,如图6 (b)所示。
3.2.3 拓扑类型与应用
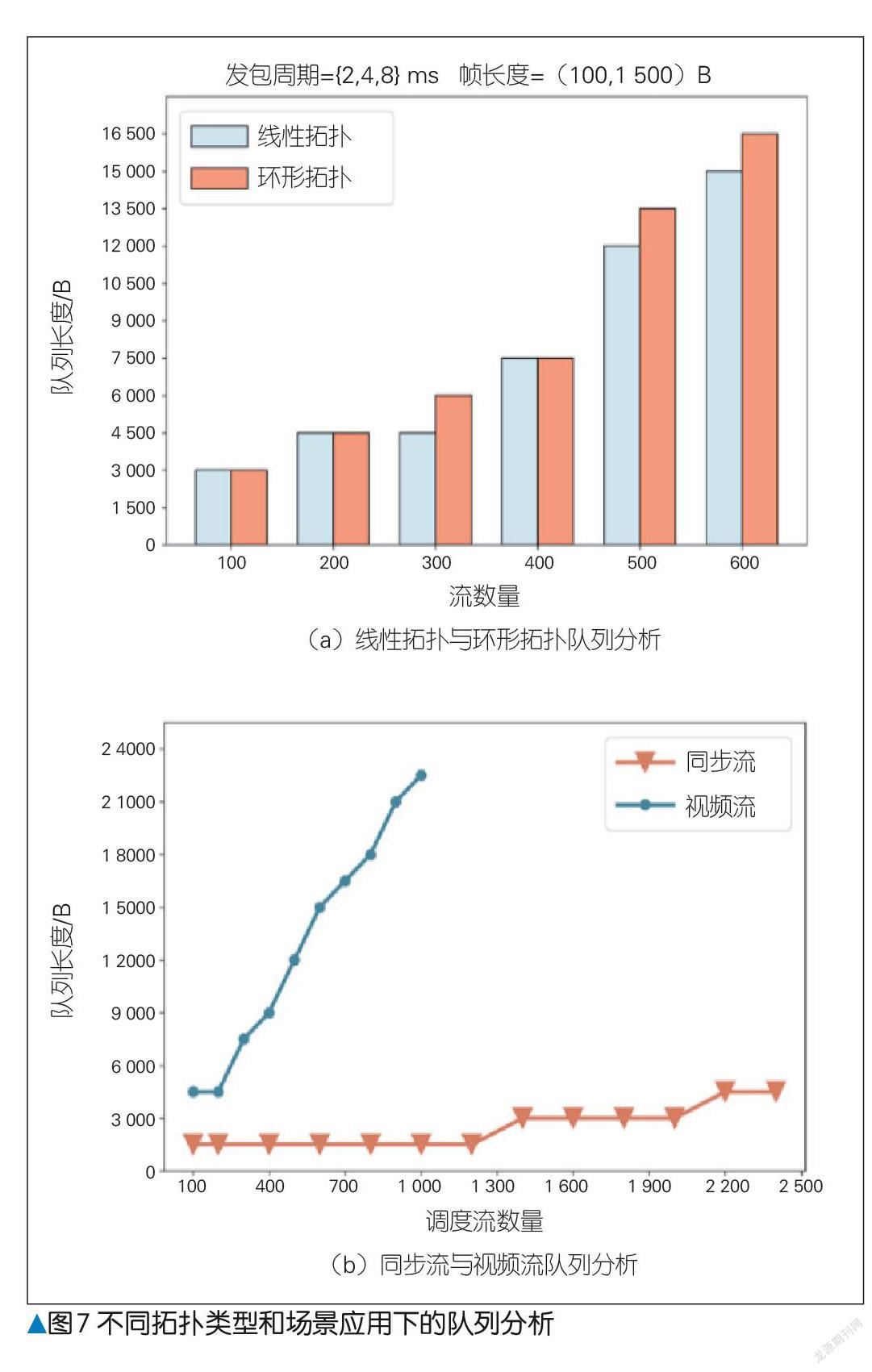
在不同网络拓扑类型下进行队列分析的实验中,我们分别采用线性拓扑和环形拓扑传输循环流,如图7 (a)所示。由于环形拓扑中所有交换机之间只能够进行单向传输,相对于线性拓扑,环形拓扑队列缓存需求更大。这说明在相同队列资源的条件下,线性拓扑可映射的流数量比环形拓扑更多[4]。
7 (b)展示了同步流和视频流的队列分析应用场景。对时延要求高、轻负载的同步流更适合短队列,可实现快速转发;对时延要求低、数据量大的视频流更适合长队列,可避免丢包。由此可见,不同类型流量和应用场景对队列长度的要求具有一定的差别,有必要根据网络流量的特性进行分析。
4结束语
随着实时性和交互性网络应用的发展,端到端有界低时延的确定性传输需求给当前网络提出了挑战,同时也为网络革新带来了机遇。TSN 作为链路层上的确定性技术正趋于完善。在本文中,我们针对 TSN 循环队列转发机制的应用进行分析研究,提出了一种队列分析优化方法,并对基于该方法的网络进行性能分析和转发队列长度选择,以优化不同场景下流的可調度性和队列资源成本,为交换机参数设置或选择提出了理论层面的建议。
参考文献
[1]黄韬, 汪硕, 黄玉栋, 等. 确定性网络研究综述[J].通信学报, 2019, 40(6):160-176. DOI:10.11959/j.issn.1000-436x.2019119
[2] IEEE. IEEE standard for local and metropolitan area networks – bridges and bridged networks - amendment 25: enhancements for scheduled traffic : IEEE [S].2015
[3] IEEE. IEEE Standard for local and metropolitan area networks – bridges and bridged networks –amendment 29: cyclic queuing and forwarding : IEEE [S].2017
[4] YAN J L, QUAN W, JIANG X Y, et al. Injection time planning : making CQF practical in time-sensitive networking [C]//IEEE INFOCOM 2020 - IEEE Conference on Computer Communications . IEEE, 2020: 616-625. DOI:10.1109/INFOCOM41043.2020.9155434
[5] QUAN W, YAN J L, JIANG X Y, et al. On-line traffic scheduling optimization in IEEE 802.1Qch based time-sensitive networks [C]//2020 IEEE 22nd International Conference on High Performance Computing and Communications; IEEE 18th International Conference on Smart City; IEEE 6th International Conference on Data Science and Systems . IEEE, 2020:369-376. DOI:10.1109/HPCC-SmartCity-DSS50907.2020.00045
[6] BOUDEC J, THIRAN P. Network calculus: a theory of deterministic queuing systems for the Internet [M]. Berlin: Springer-Verlag, 2001
[7] DE AZUA J A R, BOYER M. Complete modelling of AVB in network calculus framework [C]//Proceedings of RTNS '14: Proceedings of the 22nd International Conference on Real-Time Networks and Systems . ACM,2014:55-64. DOI:10.1145/2659787.2659810
[8] ZHAO L X, POP P, ZHENG Z, et al. Latency analysis of multiple classes of AVB traffic in TSN with standard credit behavior using network calculus [J]. IEEE transactions on industrial electronics, 2021, 68(10): 10291-10302.DOI:10.1109/TIE.2020.3021638
[9] ZHAO L X, POP P, GONG Z J, et al. Improving latency analysis for flexible window-based GCL scheduling in TSN networks by integration of consecutive nodes offsets [J]. IEEE Internet of Things journal, 2021, 8(7):5574-5584. DOI:10.1109/JIOT.2020.3031932
[10]李煥忠. 基于随机网络演算的性能分析技术研究[D].长沙: 国防科学技术大学, 2011
[11] CRACIUNAS SS, OLIVER R S, CHMELÍK M, et al. Scheduling real-time communication in IEEE 802.1Qbv time sensitive networks [C]//RTNS’16: Proceedings of the 24th International Conference on Real-Time Networks and Systems. ACM, 2016:183-192. DOI:10.1145/2997465.2997470
[12] YAN J L, QUAN W, YANG X R, et al. TSN-builder: enabling rapid customization of resource-efficient switches for time-sensitive networking [C]//2020 57th ACM/IEEE Design Automation Conference . IEEE, 2020:1-6. DOI:10.1109/DAC18072.2020.9218753
[13] WANDELER E, THIELE L. Optimal TDMA time slot and cycle length allocation for hard real-time systems [C]//Asia and South Pacific Conference on Design Automation, 2006. IEEE, 2006: 479-484. DOI:10.1109/ASPDAC.2006.1594731
[14] IEC, IEEE. Time-sensitive networking profile for industrial automation : IEC/ IEEE 60802[S].2018.
[15] Industrial Internet Consortium . Time sensitive networks ; for flexible manufacturing testbed characterization and mapping of converged traffic types [R].2019
作者简介
尹淑文,北京邮电大学在读硕士研究生;主要研究方向为确定性网络、时间敏感网络等。
汪硕,北京邮电大学讲师;主要研究方向为确定性网络、数据中心网络、软件定义网络、网络流量调度等;获 “青年人才托举工程”项目资助;发表论文20余篇,申请发明专利10余项。
黄韬,北京邮电大学教授、江苏省未来网络创新研究院副院长、紫金山实验室未来网络中心主任;主要研究方向为路由与交换、软件定义网络、内容分发网络等;先后主持科技部、工信部等重大项目10余项;获中国通信学会技术发明奖一等奖(排名第1) 1次;发表论文65篇,申请专利64项,牵头完成行业标准6 项,提交國际标准提案 25个,出版英文专著1 部、中文专著10部。
