室内温度调控问题探究
2022-04-03姚竞豪穆成昱高宇涵
姚竞豪,穆成昱,高宇涵,孙 维
(沈阳航空航天大学,沈阳 110135)
供暖系统解决了居民的采暖问题,但有时流量过小,没能使室温达到人体的舒适温度,有时流量过大使室内燥热难耐,多余的热量导致资源浪费。针对这些问题,以一间50 m2的房间为例,对其室内温度调控进行了分析并提出以下问题:
问题1:当室外温度为0℃、进水口流量为0.5 m3/h时,求房间的空间温度分布。
问题2:当室外温度为0℃、进水口流量在0.1~1变化时,求房间的动态温度分布。
1 问题分析
问题1:假设室外温度恒定,且暖气进水温度/流量都恒定,暖气内部水速恒定,房间温度分布将趋于稳定,不再随时间发生变化。采用稳态传热法进行研究,建立了房间温度分布模型,讨论房间南北方向上的温度分布。利用导热微分方程讨论房间中任意单位空间的温度传导情况,根据第二类边界条件及能量守恒定律中单位时间水的散热等于单位时间窗户、玻璃及冷风渗透散热之和,据此对微分方程进行求解,得到温度关于空间的一维分布函数。
问题2:不同流量时房间温度的动态分布。在问题1的基础上引入了一个新的维度-流量。建立了房间温度随空间与暖气流量的二维模型T(x,V),以此模型来研究不同流量下房间温度的动态分布。
2 模型假设
对房间的空间布局与设计进行了假设。房间大小为50 m2,房间高为2.8 m。房间南北为外墙,与室外接触,长为5 m,每面墙上有一扇窗户,规格为2 m×1.5 m;东西为内墙,不与室外接触,长为10 m。房间采用暖气片供热方式,共两扇,南北墙窗户正下方各一扇,每扇暖气片长2 m,高1 m。假设房间进水口每小时流量介于0.1~1 m3。建设入水口进水温度为40℃;假设水和暖气片之间不发生对流换热;假设窗户为钢窗厚度为3 cm;假设墙为一砖实心墙,厚度为24 cm;假设不发生辐射传热;假设题目所给房间和隔壁房间不发生传热。
对问题1追加假设:假设室外温度恒定为零度;假设水流速固定,为0.5 m3/h;假设暖气中水温在房间内处处相同,等于进水温度;假设外墙温度和窗户外侧温度等于外界温度;假设暖气外壁温度与相邻的空气温度相同;假设暖气回水温度为紧贴暖气侧的空气温度。
3 模型的建立与求解
3.1 温度分布模型的建立
3.1.1 基于对称分布的模型简化
由模型假设,暖气水温在房间内处处相等,且房间南北两侧传热过程同时进行,因此温度呈对称分布。以房间北侧作为研究对象,建立温度分布模型。
3.1.2 稳态导热微分方程
题设中外界温度和暖气流量及暖气入水温度恒定,因此将达到一个稳态。定义了一个微元控制体积,确认相关的能量传输过程,并引入能量传输速率方程所得,结果是一个微分方程,在边界条件给定的情况下,其解是给出介质的温度分布。

图1 体积元能量守恒演示图Fig.1 Energy conservation demonstration diagram of volume element
利用CAD绘制体积元能量守恒演示图,蓝色代表x,y,z方向热量输入,黄色代表x,y,z方向热量输出,红色为体积元中的内热元,本题没有内热元,选取x方向进行讨论。
根据能量守恒定律,温度达到平衡时,暖气产热等于房间散热和使房间内空气温度升高的热量之和。基于此确立的一维稳态传热微分方程模型如下:
T″(x)=0
3.1.3 边界条件的设立
仅用该模型求解T(0),实际暖气水温仍然为进水温度(40℃)。
A.暖气片理想散热模型。
假想暖气片为以隔热面与墙壁紧密接触,房间不再直接与墙壁进行换热,而是通过暖气片与墙壁进行间接散热。由于暖气管道内壁和水密切接触,为了简化模型,假设暖气管道内壁的温度等于入水温度。随着t(时间)的增加,房间的温度分布趋于恒定,并且在热传导中,温度分布处处连续,不会发生突变,所以将水散失热量后趋于稳定的温度视为房间T(x=0)的实际温度,即T(0)=Tw。
B.能量守恒模型。
由能量守恒定律可知:
Q产=Q散
其中,
Q产=Qw=cm(Two-Tw)
Tw0为入水温度,Tw为水散失后的温度。
Q散=Qm+Qc
其中,Qm是房间通过墙壁和窗户散失的热量,Qc是通过冷风渗透散失的热量。
C.热流密度。
在没有内热源和物性为常数的一维传热情况下,热扩散和电荷扩散之间存在着类比关系,如导电与电阻之间的关系一样,导热与热阻也存在同样的关系,热阻可以定义为驱动,是相应的传输比率,且同样存在串并联的关系。
查找了玻璃与墙壁的导热系数k1与k3,分别计算了墙壁与玻璃的热阻:
R1=h1/(S1*k1)
R3=h3/(S3*k3)
其中,h为厚度,S为面积。
由于墙与窗户为并联体系,所以平均热阻为:
Rm=(R1×R3)/(R1+R3)
墙与窗户平均热流密度为:
qm=(Tw-Tout)/(Rm*Sm)
Sm=S1+S3
总面积=墙壁面积+窗户面积。
基于查找资料,得到暖气片材质的k2(暖气片材质导热系数)。
q2=((Tw0-Tw)*k2)/h2
D.热量计算。
根据比热容计算水的产热:
Qw=cm(Tw0-Tw)
m=ρV
根据平均热流密度qm计算墙与玻璃散热:
Qm=qmSt
考虑冷风渗透[1],查阅文献[2]得知钢窗的冷风渗透量,计算了其散热:
Qc=0.278Vaρa(Tw-Tout)
E.方程求解。
将Qw,Qm,Qc代入方程解出:
Tw= 34.564℃
所以,
T(0)=Tw=34.564℃
3.1.4 一阶初值条件的求解
将暖气片假想成一张位于x=0处的隔热面,但实际并非将暖气片进行拉伸,假设原来暖气片分解为了无穷多点,让这些点均匀分布在x=0(墙壁面上),这些点面积之和不变,仍为原来暖气片面积,计算其热流密度,作为暖气片假想面的平均热流密度,根据第二类边界条件进行了求解。
根据暖气片的热流密度,由第二类边界条件列出一阶初值条件:
T″(0)=-k(Two-T(0))
3.1.5 温度场的描绘
根据微分方程及其初值条件,利用MATLAB对方程进行了求解,温度分布方程如下:
T=34.56-1.174x
绘制了房间温度和到北侧暖气距离的函数图像,如图2。

图2 0℃时房间温度变化图Fig.2 Room temperature change at 0℃
由图2可以看出,随着x的增大,房间温度单调递减,图形为线性,即单位距离下降的温度恒定,房间温度随离暖气的距离增加而线性减少。由于房间温度对称分布,在x=5到x=10,房间温度线性增加。
3.2 基于空间和入水流量的温度动态分布模型
3.2.1 房间温度动态温度模型的建立
在问题1中,基于流量为0.5 m3/h,建立了温度的空间分布模型。在问题2中,将流量作为变量,对模型进行重建。
3.2.2 能量守恒模型重建
Qw=cwVw(Tw0-Tw)
Qm=qmSmt
Qc=0.278Vaρa(Tw-Tout)
于是有:
Qw=Qm+Qc
解得:
Tw=(1.68×108V)/(4.2×106V+3.303×105)
3.2.3 温度分布模型重建
T″(x) =0
q2=((Tw0-Tw)k2)/h2
T(0)=Tw
将Tw代入微分方程组:
T(x,V)=x((3.629×107V)/(4.2×106V+3.303×105)-8.64)+(1.68×108V)/(4.2×106V+3.303×105)
利用MATLAB绘制图像如图3:
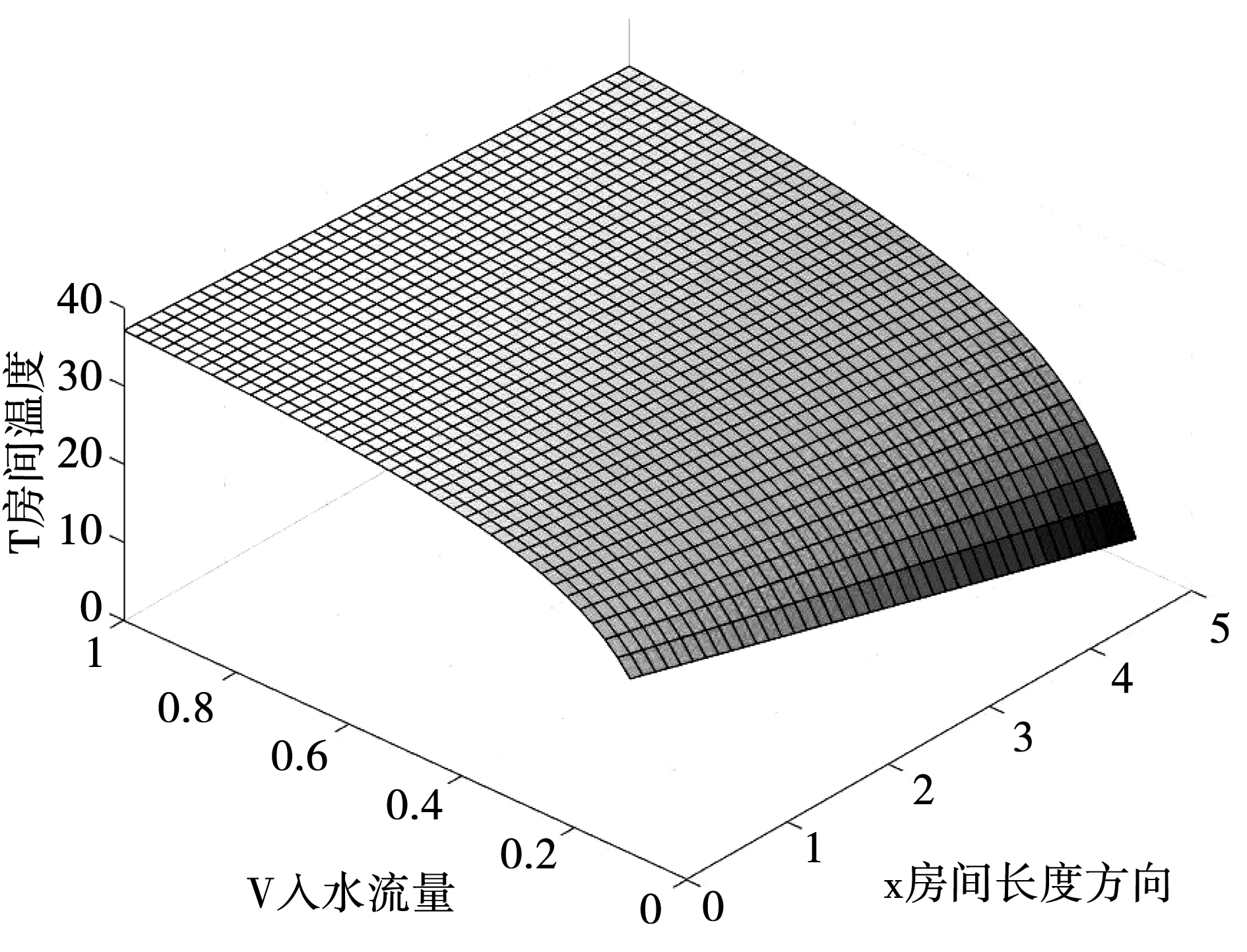
图3 室外温度0℃时房间温度随流量V,距离x变化图Fig.3 Change of room temperature on flow V and distance x at 0℃ outdoor
由图3可以看出,随着x的增大或V的减少,房间温度均呈单调递减,但它们对温度的影响程度不同,V越小,房间温度随x的下降速度越快(斜率越大)。由温度的对称分布可知,x=5到x=10处温度变化情况相同[3]。
4 模型评价
利用外围护结构散热、能量守恒和暖气产热的能量守恒及第二类边界条件和一维稳态导热微分方程描绘室内温度场的变化,考虑了流量对室内温度的影响,保证了模型的严谨性和准确性。本模型可以求解单个典型房间的温度场变化,适用范围广,可操作性强,精确度高。
