信息技术助力开展高中数学探究活动的教学实践探究

刘瑞红

【摘要】在信息技术与教育快速融合的时代背景下，有效开展高中数学探究活动迎来了新的发展契机。本文以“函数y=Asin（ωx+φ）的图象”为例，从信息技术助力开展数学探究活动的自主学习、合作学习和延伸学习三个方面，阐述了运用信息技术开展高中数学探究活动，促进发展学生数学核心素养的实践研究。

【关键词】信息技术;数学探究活动;数学核心素养

随着科学技术的飞速发展，信息技术助力教育创新迎来新的春天。作为教育工作者，我们需要积极探索信息技术赋能数学教育教学的创新做法，致力于努力发展学生的数学核心素养。下面在信息技术助力开展数学探究活动方面进行了实践探索，通过课前自主学习、课上合作学习和课后延伸学习，引导学生借助信息技术主动参与探究学习，实现线上线下、课内课外学习的融合，促进数学核心素养的发展。

一、信息技术助力开展数学探究活动的自主学习

1.创设情境  自主建模

“函数y=Asin（ωx+φ）的图象”是三角函数的一个重要内容，通过研究筒车的运动规律，学生经历y=Asin（ωx+φ）的建模过程。如果课堂上，仅仅依靠文字描述和教师讲解，不仅错失了学生进行数学探究活动的大好机会，数学抽象和数学建模的能力得不到充分发展，而且弱化了中华古代文明的育人作用。

本节课，教师可以设计问题串创设情境，引导学生类比前面建立函数模型的经验，上网搜索筒车运动和原理讲解的视频，开展自主探究性学习活动。通过观察归纳和总结发现其中的规律，体会三角函数是描述周期现象的重要数学模型，提升学生的数学建模能力，发展学生的数学抽象、直观想象、逻辑推理等核心素养。

问题1：筒车是我国古代发明的一种灌溉工具，因其经济又环保，至今还在农业生产中使用。明朝科学家徐光启在《农政全书》中用图画描绘了桶车的工作原理。请你搜索筒车运动和讲解运动原理的视频资料，研究盛水桶在运动中有何规律？可以抽象出哪些数学对象？你能想到用什么知识来刻画他们之间的关系？

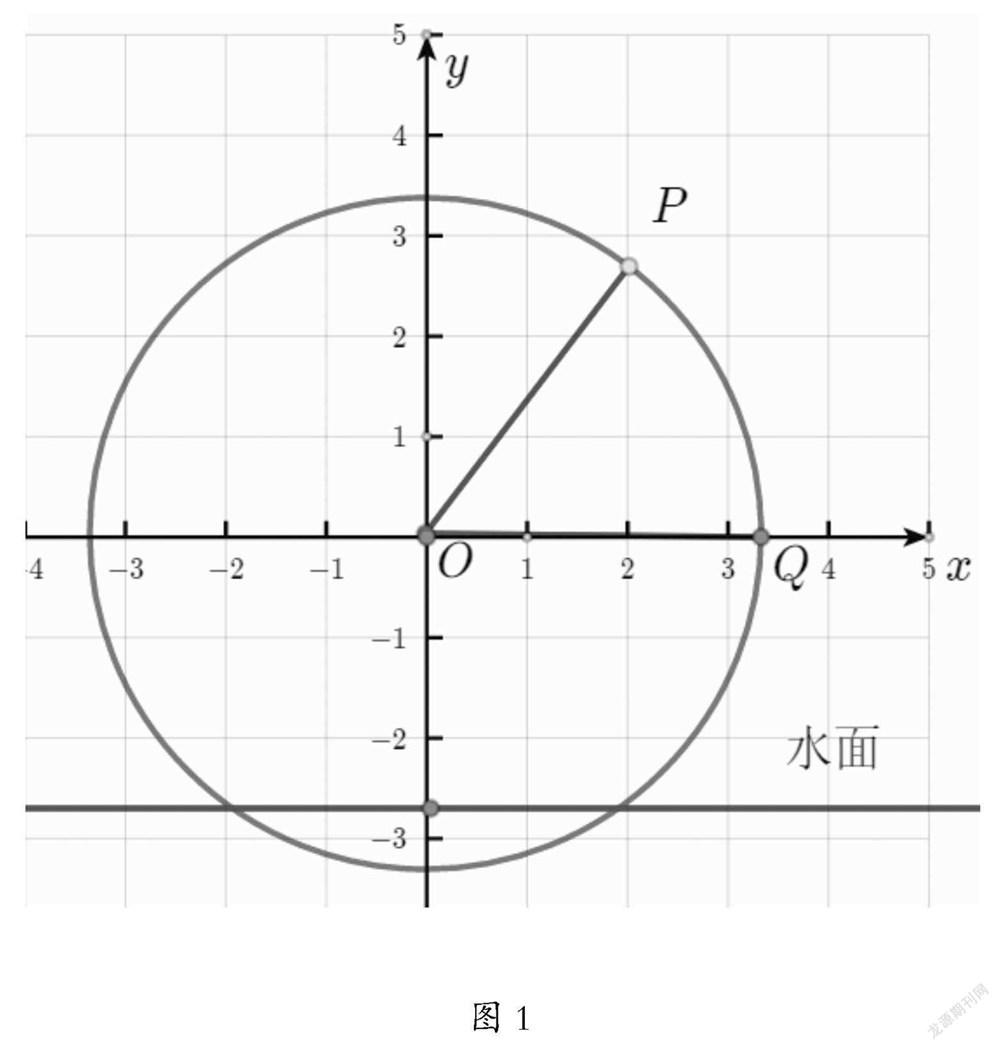
问题2：借助信息技术用几何形式动态呈现点P的运动状态（见图1）。如果已知筒车半径为r，盛水桶的初始位置Q1，对应的初始角φ及转动的角速度ω，还有筒车转轮的中心O到水面的距离h，你能刻画点P的坐标吗？

问题3：你能用函数模型刻画水桶距离水面的相对高度H与时间t的关系吗？请和同学们分享你的探究成果。

通过创设情境，拓宽学习资源，让学生经历建立筒车模型y=Asin（ωx+φ）的过程，引导学生用数学的眼光观察世界，从生活中抽象出数学模型，学会用数学的语言描述世界。同时分享探究成果给学生以成就感，老师还可以根据学生完成的情况，开展个性化、有针对性的指导，在课堂上对三角函数模型的建立进行适当的关键补充，提升教学效率。

2.搭设台阶  自主探究

在理解参数φ、ω、A在圆周运动中的实际意义后，可以在电脑室或者借助学习平板等教学设备，引导学生探究φ、ω、A对y=sin（x+φ）、y=sin（ωx+φ）（ω>0）、y=Asin（ωx+φ）（A>0）的图象影响，在探索、观察、归纳的过程中，发展数学核心素养。课上，教师提供两个学习资料，一个是网络画板呈现的可以控制系数变化的函数y=Asin（ωx+φ）（A>0，ω>0）的图象，一个是五点法作函数图象关键点的Excel列表。借助网絡画板直观演示对比，直观感知，结合关键点列表，证实结论。

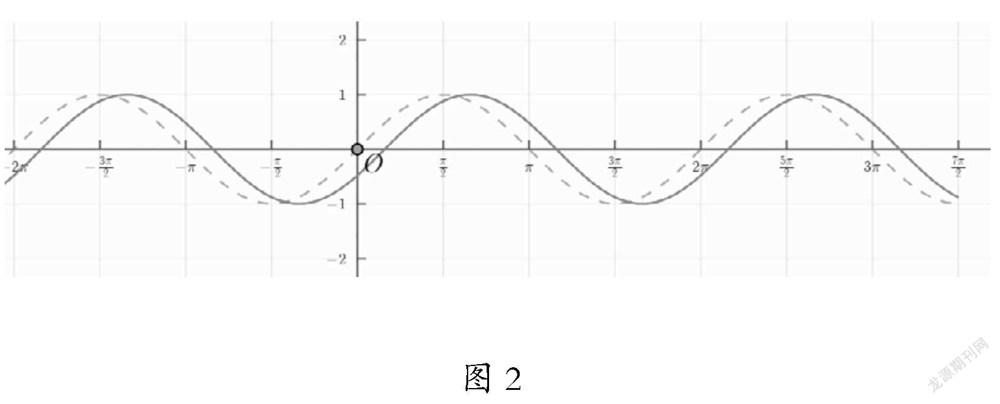
课堂预设：前面，我们已经借助单位圆得到过正弦曲线，用同样的方法，我们也可以借助网络画板作出y=sin（x+φ）的图象。（见图2）

问题4：观察φ分别取       ，    ，   时，图象发生怎样的变化？动态演示图象变化，你能否发现φ对函数y=sin（x+φ）图象有怎样的影响？

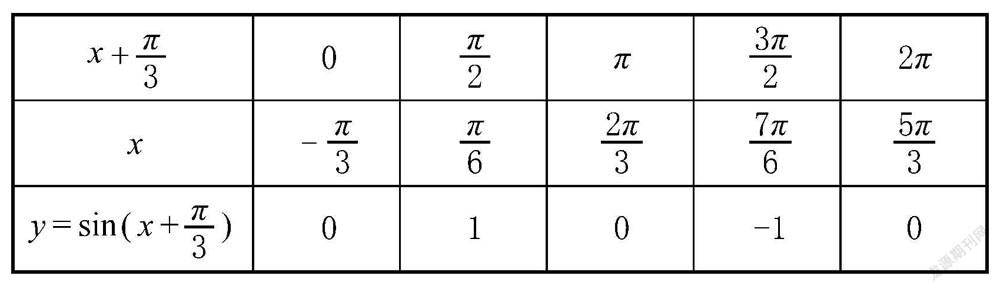
问题5：请观察下面Excel表，由“五点法”可知，函数y= sin（x+     ），x∈[0，2π]的五个关键点与函数y=sinx，x∈[0，2π]图象上的五个关键点有什么关系？请总结改变参数φ，函数y=sin（x+φ）图象可由y=sinx的图象如何变换得到？

问题6：将函数y=3cos（x+      ） 的图象向左平移

个单位所得函数图象的表达式是什么？

借助信息技术，将抽象的、动态的变化过程直观呈现给学生，加深学生对y=Asin（ωx+φ）的图象变换规律的认识，渗透数形结合思想、从特殊到一般，从具体到抽象的思维方法，发展直观想象和逻辑推理等数学核心素养。

二、信息技术助力开展数学探究活动的合作学习

在教学过程中，以学生为主体，充分借助信息技术组织数学探究活动，同时，信息技术平台促进合作学习。ω对函数y=sin（ωx+φ）（ω>0）图象的影响，既是本节课的学习重点，也是难点，由学生类比研究参数φ的方法合作探究完成。学生通过给同学分享讲授，加深他们对知识的理解和自我建构，既促进了学生在数学探究过程中自主意识的发展，又培养了他们的合作精神。

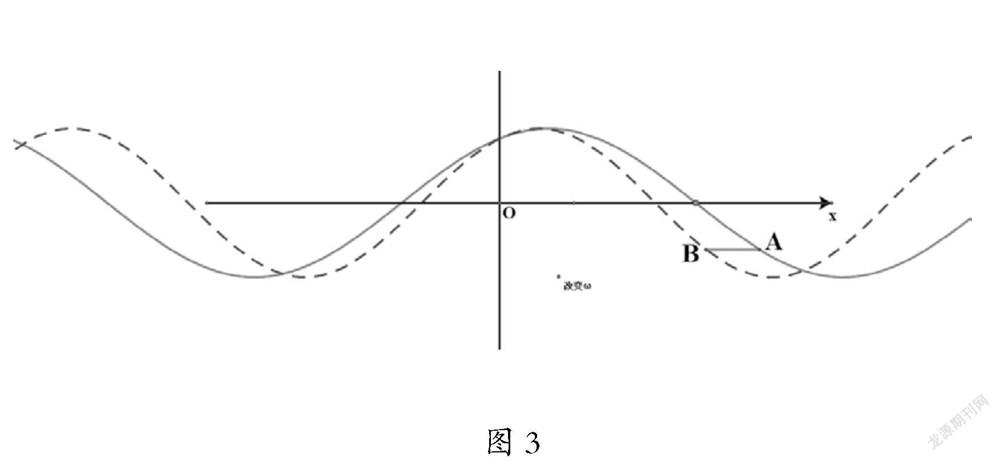
课堂预设：改变参数ω（ω>0）的值，用网络画板画出函数y=sin（2x+     ）的图象，观察分析函数数y=sin（2x+      ）与y=sin（x+      ）图象的关系。（见图3）

问题7：观察分析参数ω（ω>0）变化后，图象与y=sin（x+      ）的图象有何变换关系？你能结合ω的含义是点在圆周上运动的角速度，来分析理解发生的变化吗？

问题8：为得到y=sin（     x -     ），x∈R的图象，只需将函数 y=sin（x -     ），x∈R的图象上所有点的坐标如何变换？根据以上的实验，在ω>0且ω≠1的情况下，参数ω（ω>0）变化后，对图象的影响可分为几类？你能总结出y=sin（ωx+φ）（ω>0）可以由y=sin（ωx+φ） 的图象如何变换得到吗？

教师引导学生开展小组合作，确定研究思路，合作探究，讨论交流，借助信息技术，直观感知图象的伸缩变换，再数形结合分析坐标内在联系，加深学生理解，突破本节课的重难点，发展学生核心素养。

数学知识的抽象性往往给学习带来障碍，借助信息技术可以形象直观、动态地展现函数图象的变化联系，帮助学生提升数学抽象思维能力以及逻辑推理能力，促进学生更好地理解和掌握数学知识。

三、信息技术助力开展数学探究活动的延伸学习

信息技术助力数学教学，实现了师生之间在课前、课中和课后的持续性学习沟通，增加了課堂的深度和广度，使学习可以不断延伸。教师积极搭建平台，提供学习资源和技术支持，更好地使信息技术助力学生成长，尤其是运用信息技术的能力使学生能更好地不断自我发展。

延伸学习作业：调整变换顺序，由y=cosx的图象变换得到y=     cos（2x-      ） 的图象的变换方法是否变化？写出三种不同顺序的变换过程和方法，再用网络画板按照变换方法作出图象进行检验，说说你的发现。

通过课后延伸学习，学生借助网络画板开展数学探究活动，为下一节课继续学习y=Asin（ωx+φ）的图象变换打下基础，用网络画板作图验证，发现当ω≠1，即x的系数不为1时，平移量是         ，为突破易错点进行铺垫。

信息技术助力开展高中数学探究活动，以发展学生数学核心素养为目标，尊重学生为主体，使教学形式更多元，学习资源更丰富，学习过程更有趣。信息技术在帮助学生开展数学探究活动中的自主学习、合作学习和延伸学习方面有积极的促进作用，将抽象的数学知识以生动形象的方式呈现给学生，也将使用信息技术开展学习变成学生的一种能力，激发学生的学习兴趣，提升学生的成就感。只有让学生能够学有所获，才会喜欢学习数学，才能不断地发展自身的数学思维能力以及数学核心素养。

参考文献：

[1]刘邦奇，孙曙辉.智慧课堂[M].北京：北京师范大学出版社，2016.

[2]赵国宏.应用信息技术助力高中数学课堂教学之我见[J].数学学习与研究，2020.

[3]李久省，张程艳.发挥信息技术优势 助力高中数学学习[J].北京教育（普教版），2020.