钢-UHPC 轻型组合桥面受模拟行车扰动后抗裂性能研究

2022-04-02邵旭东莫然曹君辉陈玉宝

湖南大学学报（自然科学版） 2022年3期

邵旭东，莫然，曹君辉，陈玉宝

（1.湖南大学土木工程学院，湖南长沙 410082；2.湖南大学风工程与桥梁工程湖南省重点实验室，湖南长沙 410082）

正交异性钢桥面板具有自重轻、强度高、施工便捷等优点，但其应用同时也面临桥面铺装破损和钢桥面疲劳开裂两大难题.为此，作者所在团队提出了钢-超高性能混凝土（Ultra-High Performance Concrete，UHPC）轻型组合桥面结构（下文称钢-UHPC轻型组合桥面结构）［1］.大量理论、试验研究表明，钢-UHPC 轻型组合桥面结构具有优异的抗裂性能和疲劳性能［1-6］.

钢-UHPC 轻型组合桥面结构不仅可以应用于新建桥梁中，也可应用于在役桥梁的桥面修复工程.对于一些交通任务繁重的在役公路桥梁，完全封闭桥面进行修复工作将严重阻滞交通的正常运转.因此，往往需采取部分桥面开放交通、部分桥面封闭施工的方案以减小修复工作的负面影响［7］.然而，当新浇筑的UHPC 层尚未完全成型时，桥面行车产生的桥面往复弯拉变形和振动（下文将此作用称为行车扰动）有可能导致UHPC 开裂，对本结构的抗裂性能产生不利影响，但目前针对这一问题的研究甚少.

对于新浇普通混凝土材料和结构受行车扰动后的力学性能，国内外学者已进行了一些研究［8-11］.李雷等［8］研究了铁路桥梁上列车振动对混凝土力学性能的影响，发现在初凝后1 h起振及持续振动的混凝土试块受振动后损伤最为严重，且混凝土如在不同时间点均受振动，其内部损伤会积累.张悦然等［9］的研究表明，混凝土在凝结硬化中期受振动时强度损失最严重.Shraddhakar［10］通过模型试验，研究了混凝土桥梁桥面修复工程中行车振动的影响，发现只要使用较低坍落度的高品质混凝土，车辆扰动对混凝土抗压强度、混凝土与钢筋间的黏结性能无不利影响.Furr 等［11］进行了实桥试验，结论为在跨径100 英尺以下的梁桥桥面加宽工程中，新浇筑的混凝土接缝不会受到附近交通扰动的不利影响.

当前，学界对UHPC 受扰动后性能的研究仍较少.徐亚林等［12］通过电磁振动实验台在不同阶段对新浇筑的UHPC 施加了2 Hz-3 mm、4 Hz-1 mm、4 Hz-3 mm 三种参数的振动，研究了车桥耦合振动对UHPC 钢桥面铺装工程中UHPC 材料抗压强度的影响.研究结论为，车桥耦合振动作用下UHPC 的抗压强度均有不同程度提高，但在初凝—终凝期间受振时抗压强度提高程度最小，相比对照组无明显增长；此外，较低的振动幅度、较高的振动频率对UHPC抗压强度更有利.

由于试验方法、混凝土材料和针对的结构类型不尽相同，不同学者对混凝土受扰动后力学性能的研究结论存在一定差异甚至矛盾.另外，当前尚缺乏针对钢-UHPC 轻型组合桥面结构施工中受行车扰动产生往复弯拉变形后抗裂性能的研究.因此，本文将施工过程中桥面行车引起的UHPC 层顶面最大拉应变定义为“扰动幅度”，以重庆鱼嘴长江大桥为背景，开展了理论和试验研究，重点探究不同扰动幅度下UHPC 层的开裂情况和结构受扰动后的抗裂性能，为实际施工中的桥面交通方案制订提供指导.

1 工程概况

鱼嘴长江大桥（下文简称鱼嘴大桥）为西部开发省际公路通道重庆绕城公路东段跨越长江的一座特大型桥梁.如图1 所示，大桥为主跨616 m 的单跨双铰简支钢箱梁悬索桥，加劲梁梁高3.0 m，全宽36.8 m，双向6车道设计，采用正交异性桥面板，标准段顶板厚14 mm，顶板加劲肋为8 mm 厚的U 形闭口肋.设计采用14 mm 钢桥面板+45 mm UHPC 层+7 mm 薄层聚合物罩面（Thin Polymer Overlay，TPO）层的钢-UHPC轻型组合桥面结构.

图1 鱼嘴大桥结构布置图Fig.1 Layouts of Yuzui Bridge

为避免交通全封闭带来的不利影响，桥面施工采用半幅桥面浇筑、半幅桥面通车方案，如图2 所示.以下将封闭施工的桥面简称为“施工幅”，将开放交通的桥面简称为“通车幅”.

图2 半幅桥面开放交通的施工方案Fig.2 Construction scheme of half the deck open to traffic

2 有限元计算

2.1 Midas全桥有限元模型

2.1.1 模型概况

首先通过Midas建立全桥杆系有限元模型，分析第一体系下桥面行车对施工幅UHPC 层的最大纵向扰动幅度εuz-d.

大桥的主塔、加劲梁采用梁单元模拟，主缆和吊杆均采用只受拉桁架单元.考虑到刚浇筑时UHPC层弹性模量很低［13］，层内钢筋也尚未能参与受力，因此模型中的加劲梁采用纯钢梁截面进行计算，未模拟UHPC层.模型使用的材料特性见表1.

表1 Midas模型使用材料属性Tab.1 Material properties in Midas finite element model

计算仅关注车道荷载导致的UHPC 变形，在桥面中心线一侧施加3 车道（通车幅桥面最大通行车道数）的公路-Ⅰ级荷载，从而模拟半幅桥面施工、半幅桥面通车的工况.由于UHPC 在施工中受到的扰动属于短暂荷载状况，因此在计算扰动幅度时应按施工阶段的应力验算进行.根据我国《公路桥涵通用设计规范》（JTG D60—2015），汽车作用采用标准值，作用分项系数为1.0.计算中考虑了汽车冲击系数、横向折减系数和纵向折减系数［14］，偏载系数取1.15［15］.

2.1.2 计算结果

全桥UHPC 层顶面纵向拉应变包络图如图3 所示.由图3 可知，在离加劲梁梁端约16%主跨长度处，UHPC层受到的纵向扰动幅度最大.

图3 UHPC层顶面纵向拉应变包络图Fig.3 Longitudinal tensile strain envelope diagram of UHPC layer’s top surface

计算得到的全桥钢桥面板最大纵向拉应变εsz-d为112 με.如图4 所示，由于模型中的加劲梁截面无UHPC 层，UHPC 所受最大纵向扰动幅度εuz-d由εsz-d按平截面假定计算得到.εuz-d的计算结果为117 με.

图4 UHPC层最大扰动幅度计算值εuz-d计算方法Fig.4 Calculation method of the maximum disturbance amplitude of the UHPC layer εuz-d

需要说明的是，在计算实桥的最大扰动幅度时，忽略UHPC 层刚度后，截面整体刚度更低，钢梁顶板受力更大、拉应变更高；同时，UHPC顶面和钢梁顶板到截面中性轴的距离之比也更大.因此，计算得到的最大扰动幅度偏于安全.

2.2 ANSYS局部有限元模型

2.2.1 模型概况

依照作者团队以前相关研究的建模方法［5-6］，通过ANSYS 建立加劲梁的局部有限元模型，从而分析局部车辆荷载的作用.模型总长48 m（取4个标准梁段长度），总宽34.8 m（加劲梁全宽）.加劲梁采用SHELL63 壳单元模拟，施工幅桥面的UHPC 层采用SOLID185 实体单元模拟.仅进行线弹性计算且不考虑UHPC的刚度.

车辆荷载选用标准车辆模型［14］.在横向，通车幅桥面的行车道内侧需布置施工设备，因此车辆靠行车道外侧行驶，共布置3 辆并排行驶的标准车，车辆间距按规范取值［14］.在纵向，于模型中段共设置7 个纵向位置，车辆每次向前行驶4 m.局部模型的冲击系数取为0.4［16］.

对于模型起止端截面上的节点，约束其纵向平动自由度、横向平动自由度以及绕竖轴与横轴的转动自由度，模拟相邻梁段对这两个截面的约束作用；在有吊杆的横隔板处，按吊杆的实际设计位置，约束横隔板对应位置节点的竖向平动自由度以模拟吊杆的约束作用.

2.2.2 计算结果

局部计算表明，车辆荷载的局部效应显著，因此前后车对扰动幅度的计算结果影响近似为零，在局部计算中不考虑前后车的叠加作用是合理的.

图5以纵向拉应变为例，给出了施工幅UHPC 层顶面在出现最大拉应变时的应变分布情况.

计算结果表明，当通车幅开放3 车道交通时，车辆荷载对UHPC 的最大纵向扰动幅度为27 με，最大横向扰动幅度为60 με.由于受到较强的竖向局部支撑，UHPC 在有吊杆的横隔板截面处受到的纵、横向扰动幅度更大.由图5 可知，最大纵向拉应变位于有吊杆的横隔板上方.

图5 UHPC层顶面出现最大拉应变时的纵向应变分布Fig.5 Longitudinal strain distribution of the UHPC layer’s top surface when the maximum tensile strain occurs

2.3 计算结果叠加

如表2 所示，将全桥模型与局部模型的计算结果进行线性叠加.由表2 可知，在开放3 车道交通的条件下，全桥施工幅UHPC 层受到的最大纵向扰动幅度为144 με，最大横向扰动幅度为60 με.

表2 全桥模型与局部模型计算结果叠加Tab.2 Superposition of analysis results of the full-bridge model and the local model

虽然局部模型中车辆荷载的横向扰动幅度大于纵向扰动幅度，但综合全桥模型和局部模型的计算结果后认为，桥面行车对施工幅UHPC 的扰动作用仍以纵向扰动为主.因此下文的扰动试验以纵向扰动作为依据进行设计.

3 试验方案

3.1 试验内容和步骤

试验分为模拟行车扰动试验（简称扰动试验）和静力试验两个阶段：在扰动试验中，通过疲劳机作动器对试件施加周期变化的荷载，以此模拟实际工程中结构受到的行车扰动；在静力试验中，对试件进行四点负弯矩静力加载直至破坏，然后将扰动试验的结果与对照试件的静力试验结果进行对比.具体试验方案将在3.3～3.4节中详细介绍.

UHPC 在高温蒸汽养护前需完成终凝且具有一定的强度，根据以往的本结构相关研究和工程实践，在浇筑UHPC 之后需自然养护2 d，然后在90～100 ℃的环境下高温蒸汽养护48 h［1-6］.因此本试验也采取了这一养护制度.主要试验步骤为：1）制作钢梁，焊接栓钉并铺设钢筋网，搭设UHPC 层模板；2）浇筑UHPC，进行自然养护，养护期间进行扰动试验；3）扰动结束后，对试件进行蒸汽养护；4）进行静力试验.

3.2 试件设计

根据本桥拟采用的桥面结构方案，制作了6 个带单个U肋的钢-UHPC轻型组合桥面结构模型试件（以下简称“试件”），每3个为一组，共分为2组.在每组试件中，2 个试件在UHPC 凝结期间接受扰动，称为“扰动试件”；另1 个试件不受扰动，称为“对照试件”.

试件的具体尺寸和构造如图6 所示，其中纯弯段长度为450 mm.钢梁材料为Q345 桥梁用钢.所采用的UHPC 是湖南大学研究团队研发的钢桥面专用材料，其钢纤维体积掺量为3.5%.纵、横向钢筋间距均为37.5 mm.在钢梁顶板焊接φ13 mm × 35 mm 的短栓钉，间距150 mm×150 mm.

图6 试件尺寸和构造（单位：mm）Fig.6 Dimensions and details of specimens（unit：mm）

3.3 扰动试验的试验参数

3.3.1 扰动幅度

根据上文的计算结果，设置第1 组试验的纯弯段扰动幅度εu=160 με，与表2 中的εuz-d基本相当；第2 组试验的纯弯段扰动幅度εu=240 με，较第1 组提高50%.

由于无法直接在未完全凝结的UHPC 表面粘贴应变片，因此将应变片布置在钢梁纯弯段顶板两侧翼缘的下表面（如图7（a）所示），试验中通过调整翼缘下表面最大拉应变εs来控制扰动幅度εu.假设试件变形符合平截面假定且UHPC 层刚度为零，则通过计算可知，第1 组试验和第2 组试验的εs分别应控制为82 με和123 με，如表3所示.另外，为了使振幅尽量大，同时保持加载装置的稳定，根据以往经验，钢梁翼缘下表面最小拉应变控制为最大拉应变εs的20%左右.

图7 扰动试验应变片布置和加载方式（单位：mm）Fig.7 Strain gauges layout and loading scheme of disturbance tests（unit：mm）

此外，对表3有几点需要说明：

1）在扰动试验中，随着UHPC 的弹性模量逐渐形成，截面刚度提高，相同荷载下试件的变形将减小；由于试验中UHPC 的模量在持续变化、难以实时掌握截面的刚度，因此在试验过程中偏保守地适时提高荷载，控制εs基本保持为定值；当εs不变时，随着截面中性轴上移，εu将提高，因此表3 中的εu为变化的值.

2）表3 中εu的上限值是基于扰动结束时UHPC已完全形成弹性模量，钢筋充分参与受力的假设计算得到的（UHPC 弹性模量为43.4 GPa，见表4）；实际上，UHPC 层在扰动结束但还未开始蒸汽养护时，其刚度仍未完全形成，因此计算得到的上限值偏大.

3）考虑到扰动试验中裂缝的形成是损伤逐渐累积的结果，本文偏谨慎地以各组的预设扰动幅度（即表3 中εu的下限值）作为扰动幅度的评判标准，εu的上限值仅用于辅助体现试验中扰动幅度有所上升的特点，说明本试验方案是偏安全的.

表3 顶板下表面最大拉应变和UHPC扰动幅度Tab.3 Maximum tensile strains of the top plate’s lower surface and disturbance amplitudes of UHPC

规定扰动试件的命名方式为“RD-本组扰动幅度-编号”，而对照试件命名方式为“DZ-本组组号”.因此第1组试件命名为：RD-160-1、RD-160-2和DZ-1；第2组试件命名为：RD-240-1、RD-240-2和DZ-2.

3.3.2 扰动频率和时长

根据文献［12］报道的研究方案和实际试验条件，本文选择2 Hz 作为扰动加载频率.相关研究表明，扰动对初凝前的混凝土无不利影响，而对初凝到终凝状态之间混凝土的影响较显著［7，9，12］，考虑到加载前安装、调试设备的需要，扰动起始时间选择在UHPC初凝之后.持续扰动24 h后对UHPC进行高温蒸汽养护.UHPC初凝时间按标准方法测试［17］.

3.4 试验装置

在扰动试验中，由于UHPC 尚未完全凝结，因而按图7（b）所示方式进行加载.通过疲劳机作动器给分配梁施加向下的、频率为2 Hz的正弦波压力，分配梁再将荷载传递到试件的两个悬臂端，使试件受负弯矩作用，UHPC 层受拉.钢梁顶板翼缘底面拉应变的实测波形如图7（c）所示，实际加载装置如图8所示.

图8 实际扰动试验加载装置Fig.8 Actual loading devices in disturbance tests

在静力试验中，使用MTS（Mechanical Testing and Simulation System）进行四点负弯矩加载，加载装置和位移表设置如图9（a）所示.百分表D1～D3 用于测量挠度.在UHPC层纵向起止端的两侧各布置2个千分表，表架的基座固定于钢梁翼缘板底面，千分表的测头与固定在UHPC 层侧面的角钢接触，从而测量UHPC 层与钢梁顶板间的相对滑移.在纯弯段UHPC 顶面选取4 个截面，每个截面沿横向布置5 个应变片，共布置20个应变片，如图9（b）所示.

图9 静力试验的试验装置和应变片布置（单位：mm）Fig.9 Test devices and strain gauges layouts of static tests（unit：mm）

4 试验结果

4.1 UHPC材料基本性能

在浇筑每组UHPC 模型试件的同时制作用于UHPC 材料性能试验的小试件，包括3 个100 m ×100 m×100 mm的立方体抗压强度试件，3个100 m×100 m×400 mm的棱柱体抗折强度试件和3个100 m×100 m × 300 mm 的棱柱体弹性模量试件.这些小试件与模型试件在相同条件下进行养护.蒸汽养护结束后，按标准方法［18］测试并计算得到UHPC 的基本力学性能指标，如表4所示.

表4 UHPC基本力学性能试验结果Tab.4 Results of UHPC mechanical tests

4.2 试件有限元模型计算

为了对试件的受力状态有更清晰的了解，同时验证试验结果的合理性，使用有限元软件ANSYS 建立了试件的有限元模型进行模拟分析，如图10所示.

图10 试件有限元模型Fig.10 Finite element model of specimens

钢梁和UHPC 层均采用SOLID185 实体单元进行模拟；纵向钢筋用LINK180 杆单元模拟；由于横向钢筋不参与试件的纵向受力，因此未模拟横向钢筋.假定UHPC 层与钢梁始终作为整体结构共同受力，对UHPC层下表面与钢梁顶板上表面作共节点处理.

在针对扰动试验的有限元模型中，所有材料均为线弹性材料.钢的泊松比为0.3，弹性模量为206 GPa.UHPC 的泊松比为0.2，弹性模量为10-6GPa，相当于不考虑UHPC 层对结构刚度的影响.该模型不模拟纵向钢筋.对该模型进行谐响应分析和静力分析，以考虑扰动荷载的动力放大作用.

在针对静力试验的有限元模型中，UHPC材料性能采用表4 所示的实测值，并根据文献［19］将UHPC的受拉本构简化为双折线模型.钢板和钢筋的本构也取为双折线模型，屈服强度分别为389 MPa（厂家提供）和400 MPa（抗拉强度标准值［20］）.本模型仅进行静力分析.

模型的加载方式和约束与实际一致.有限元计算结果将在下文与试验结果共同呈现.

4.3 扰动试验结果及分析

在扰动过程中、扰动完成和蒸汽养护结束后持续观察UHPC 表面是否有裂缝产生.在扰动完成和蒸汽养护结束后，还需先对试件表面进行适当打磨以去除表面浮浆并保证UHPC 表面的清洁平整，从而更好地观测裂缝.对于观测到的裂缝，用记号笔沿裂缝路径作好标记以便后续试验的进一步研究.两组试件的扰动裂缝或裂缝痕迹如图11所示.

图11 扰动裂缝和裂缝痕迹Fig.11 Cracks caused by disturbance

第1 组试件在扰动过程中均未发现裂缝.扰动结束后，在RD-160-2 横隔板附近UHPC 顶面发现2条细长的纹路，但尚不能确定是否为裂缝；在蒸汽养护结束后，RD-160-1和DZ-1仍未观测到裂缝，但前述的RD-160-2 上的两条纹路形成了张开的细小裂缝（记1 号和2 号裂缝），同时在纯弯段中部观测到3条新形成的细裂缝（记3～5 号裂缝），如图11（a）所示.对于1、2 号裂缝，由于在蒸养前已观测到其纹路，因此这两条裂缝有可能是扰动导致的；对3～5 号裂缝，由于在蒸养前未发现其痕迹，因此推测这几条裂缝形成的原因为：在蒸养开始时升温梯度未控制好、温度提升较快，导致UHPC 层内外温差过大进而开裂.

在第2 组试件的扰动试验中，扰动开始约6～7 h后，两个扰动试件的UHPC 层顶面均出现了明显的横向裂缝.裂缝位于试件两个横隔板附近，在横向从钢梁顶板和横隔板连接处向两边延伸.但是，UHPC在浇筑后会在其表面形成一层较薄的浮浆层，浮浆层的强度较低，容易开裂.所以在扰动结束后，打磨UHPC 表面除去浮浆层，重新检查开裂情况.打磨后的扰动试件纯弯段UHPC 层顶面如图11（b）（c）所示，经过打磨，在UHPC 层顶面上述裂缝路径位置仍有凹痕，但尚未形成张开的裂缝.因此可以判断这些扰动裂缝深度较浅，仅位于UHPC 表面的浮浆层内，但UHPC内部结构仍可能受到了损伤.

由图12 和表5 的有限元计算结果可知，在纯弯段中部区域，UHPC顶面所受扰动幅度与本组试验设定的扰动幅度较为接近；而在横隔板附近，由于钢梁顶板受到横隔板的支撑作用，在弯剪耦合作用下，UHPC 顶面在钢梁顶板与横隔板连接处的纵向拉应变较高、UHPC 受到的扰动幅度更大.这也解释了为什么UHPC在此处更易受损或开裂.

图12 UHPC顶面纵向拉应变分布Fig.12 Longitudinal strain distribution on the top surface of the UHPC layer

表5 扰动实验扰动幅度的有限元计算结果Tab.5 Finite element analysis results of disturbance amplitudes in disturbance tests

此外，注意到，第2 组扰动试件纯弯段中部的扰动幅度与第1 组试件横隔板附近的扰动幅度基本相当，但第2 组扰动试件纯弯段中部皆未观测到扰动裂缝或裂缝凹痕，这与两组试验UHPC 的材料性能存在一定差异有关.

4.4 静力试验结果及分析

4.4.1 荷载-跨中挠度曲线

在进行第一个试件RD-160-1的静力试验时，由于设计的横隔板厚度较薄，荷载达到750 kN 时横隔板失稳，导致试验终止.剩下的5 个试件加强了横隔板，其极限承载力显著提高.试件的荷载-跨中挠度曲线如图13 所示，试件跨中挠度由图9（a）中的百分表D1～D3 的测量结果计算得到，图13 中“计算-1”“计算-2”分别为两组试件的有限元模型计算得到的曲线.

图13 表明，各试件跨中挠度随荷载变化的规律基本一致，大致可以分为3个阶段：线性段、刚度折减段和下降段.在接近极限荷载时（1 590～1 610 kN），U 肋下部突然发生屈曲，如图14 所示，U 肋屈曲后，试件跨中挠度迅速增加，荷载-跨中挠度曲线趋于水平但仍略有上升，随后进入下降段.

图13 荷载-跨中挠度曲线Fig.13 Load-midspan deflection curves

图14 U肋屈曲Fig.14 Buckling of U-rib

同时，由图13 可知，扰动试件与对照试件的荷载-跨中挠度曲线差异较小.在0～1 000 kN时，荷载-跨中挠度曲线近似为直线，扰动试件与对照试件的跨中挠度较接近且曲线斜率基本一致；大约在900～1 000 kN时，U肋底面钢板开始屈服，试件的荷载-跨中挠度曲线开始呈现较明显的非线性，此时结构内部受力复杂，各试件的荷载-跨中挠度曲线呈现出一定的差异性，但在相同荷载水平下试件刚度的大小和变化趋势仍十分相似.此外，有限元计算结果与实测结果总体吻合较好，但极限荷载偏低，且在荷载为1 000～1 400 kN区段计算结果偏小.

4.4.2 荷载-UHPC顶面平均应变曲线

试件纯弯段UHPC 顶面平均应变与荷载的关系如图15所示.

图15 荷载-UHPC顶面平均应变曲线Fig.15 Load-average strain of UHPC top surface curve

由于UHPC 中纤维分布的随机性以及养护中环境温度和湿度等外在条件的影响，UHPC 性能存在一定波动，因此测量得到的荷载-UHPC 顶面平均应变曲线可能呈现较明显的离散性.但总体而言，扰动试件与对照试件的曲线变化趋势基本一致，扰动对UHPC顶面应变增长规律的影响不显著，说明行车扰动对UHPC层的整体受力特性无显著影响.

另外，有限元计算结果与实测结果总体吻合较好，但由于难以模拟钢梁屈曲、试件承载力下降等复杂非线性现象，因此有限元计算曲线未出现下降段.

4.4.3 荷载-界面滑移曲线

行车扰动可能会造成UHPC 层与钢桥面板的连接性能受损，因此试验还关注了UHPC 层与钢梁顶板间的界面滑移.为体现试件滑移大小的平均水平，将图9（a）中的4 个千分表测量的滑移数据取平均值作为此试件整体的滑移量，绘制出两组试件界面滑移量随荷载变化的曲线，如图16所示.

图16 荷载-界面滑移曲线Fig.16 Load-interface slip curves

由图16 可知，两组试验的试验结果存在较大的离散性，主要原因在于：1）UHPC 与钢板间的自然黏结作用较为复杂，受影响因素多，给试验结果引入较大不确定性；2）所有试件在极限荷载下的滑移量均不超过0.08 mm，远低于规范规定的正常使用极限状态验算滑移限值0.2 mm［20］，由于滑移绝对值小，测量精度要求高，因此也容易产生较大的相对误差.但总体来看，各曲线的发展趋势较为稳定，扰动试件与对照试件界面滑移曲线未展现出明显差异.

相关研究表明，相对滑移将使组合结构刚度减小，挠度增加［22］.结合图13、图15 和图16 以及4.4.1～4.4.3节的分析可知，对于每组试件，虽然试件的滑移量存在一定差别，但各试件在荷载作用下的变形响应特性十分相近，试件间的刚度差异较小且刚度的相对大小与滑移量关联性很低，说明静力试验中UHPC 层与钢梁顶板间的滑移未对试件的整体刚度产生显著影响.

一方面，在第2 组预设幅度为240 με 扰动作用下，扰动对UHPC 层和钢桥面板间连接性能的影响仍不显著；另一方面，本结构UHPC 层和钢桥面板的连接十分紧密，静力试验中两者始终有效协同受力.因此可以推断，扰动幅度不大于240 με时，行车扰动对本结构的UHPC 层与钢桥面板连接性能的影响很小，不足以对本结构的整体刚度造成实际损害.

4.4.4 裂缝分析

各试件的荷载-最大裂缝宽度关系如图17 所示，纯弯段UHPC 层顶面裂缝的开展特点如图18 所示.在静力试验中，UHPC 层经历了无可见裂缝、产生可见裂缝、主裂缝扩展3 个阶段.加载初期，结构近似处于线弹性阶段，此时UHPC 无可见裂缝.在200～300 kN 时，横隔板附近的UHPC 层顶面因为应力水平更高而率先产生宽度为0.01～0.02 mm 的横向裂缝.随后，各试件的最大裂缝宽度大致随荷载增加而线性增长，此时裂缝发展速度很慢.在荷载达到800～1200 kN 后，构件整体刚度明显减小、变形显著增大，裂缝宽度的发展速度大幅提高，这一现象主要由U肋钢板屈服引起.

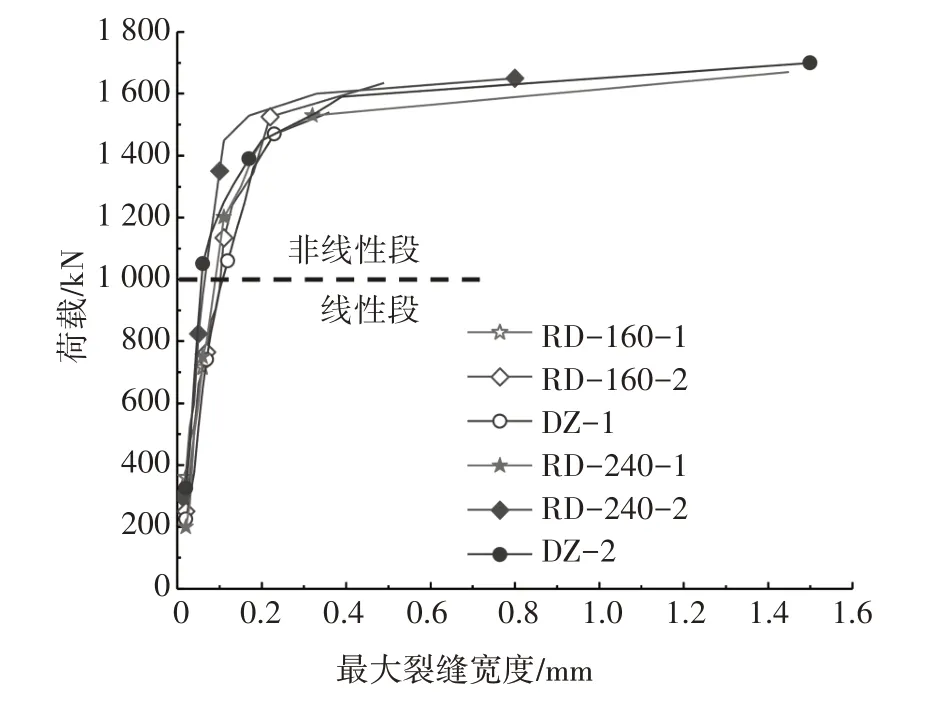
图17 荷载-最大裂缝宽度曲线Fig.17 Load-maximum crack width curves

如图18（a）所示，各试件纯弯段UHPC 层顶面的初裂缝和主裂缝均位于虚线框所示的横隔板位置附近.在静力试验中，两组扰动试件纯弯段中部UHPC 的裂缝开展特点与对照试件基本相同，但横隔板附近的裂缝普遍形成更早、扩展更快.对于扰动试件RD-160-2、RD-240-1 和RD-240-2，横隔板附近的主裂缝基本都沿着之前的标记路径展开，如图18（b）所示.

图18 静力试验中裂缝开展特点Fig.18 Cracking characteristics in static tests

4.4.5 名义开裂应力对比

文献［23］表明，宽度在0.05 mm及以下的裂缝对UHPC 的耐久性无不利影响.因此，将UHPC 表面最大裂缝宽度为0.05 mm 时的应力定义为名义开裂应力，对应的荷载定义为名义开裂荷载.

如4.3 节所述，横隔板上方的UHPC 应力显著高于纯弯段中部的应力；在静力试验中，横隔板上方的UHPC 最先开裂且裂缝宽度最先达到0.05 mm.因此将每个试验得到的开裂荷载输入有限元模型中，按线弹性计算，然后提取横隔板正上方UHPC 顶面所有节点的纵向拉应力值取平均作为本试件的UHPC名义开裂应力值.各试件的名义开裂荷载和名义开裂应力如表6所示，由于两组试件的UHPC 材料性能存在一定差异，因此第2 组试件的名义开裂应力均高于第1组试件.

表6 名义开裂荷载与名义开裂应力Tab.6 Nominal cracking loads and nominal cracking stresses

由表6 可知，在第1 组试件中，两个扰动试件的名义开裂应力仅略低于对照试件，扰动试件名义开裂应力的平均降幅为6.3%.第2 组扰动试件的名义开裂应力相比本组对照试件的平均降幅为18.8%，降幅大于第1 组.两组扰动试件名义开裂应力下降的原因均在于横隔板附近UHPC 层受到的扰动幅度显著高于本组扰动试验设定的扰动幅度，导致此处结构受到损伤或开裂，因此在静力试验中该位置的裂缝扩展速度相对较快.

此外，注意到第2 组两个扰动试件的名义开裂应力的降幅相差较大，推测其主要原因为：在浇筑第2 组试件时，由于试验条件限制，RD-240-1 和RD-240-2 只能分两次浇筑，先后施加扰动，最后一起进行高温蒸汽养护；由于在扰动试验中环境的温度、湿度等不完全一致，两个扰动试件在接受扰动时UHPC水化程度存在差别，扰动造成的材料损伤不同，因而在静力试验中的名义开裂应力相差较大.但是，RD-240-1和RD-240-2在扰动过程中UHPC浮浆层均开裂，且其名义开裂应力相对本组对照试件的降幅均高于第1 组的相应降幅，说明由于本组的扰动幅度更大，扰动试件UHPC层受到的损伤更为显著.

综合以上试验现象及表5和表6的计算结果，可以偏谨慎地判断：当行车扰动幅度不高于160 με时，结构的抗裂性能基本不会受到影响；当扰动幅度超过160 με 后，UHPC 层将受损甚至开裂，导致结构的抗裂性能下降.因此，实际施工中UHPC 所受行车扰动幅度的限值建议取为160 με.由于本文以UHPC层顶面的最大拉应变作为衡量扰动幅度的指标，考虑到UHPC 受到的纵、横向弯拉扰动的受力模式基本一致，因此该限值对横向扰动幅度的验算同样适用.