自适应巡航控制系统的设计及硬件在环仿真
2022-04-02李世豪
黄 鹏,何 通,李世豪
(长安大学 汽车学院,陕西 西安 710064)
目前自适应巡航控制系统着重单一稳态跟随工况的研究,然而现实中交通环境是多样和随机的,及时恰当的模式切换策略对于自适应巡航控制(Adaptive Cruise Control, ACC)系统有着关键意义。文献[1]为尽可能消除模式切换时加速度跳变现象,采用加速度加权平均算法来减少车辆在模式切换过程中的抖振,但该方法无法彻底消除这一现象。文献[2]提出一种在定速巡航模式下虚拟前车的方法,与常规模式切换策略相比系统响应更加平稳。本文上位控制器的设计采用线性二次型调节器(linear quadratic regulator, LQR),并在虚拟前车方法的基础上设计了模式切换策略。
硬件在环仿真测试可以在实车测试前对控制器进行功能验证,对于开发周期的缩短和成本的降低均有重要意义。文献[3]对设计的自适应巡航控制器在Matlab/Simulink中建立系统模型进行仿真。文献[4]对设计的 ACC 系统在 Carsim 和Simulink中进行典型工况联合仿真试验。文献[3]和文献[4]对ACC系统的测试均在纯仿真阶段。文献[5]对设计的考虑车间反应距离的 ACC系统进行了实车试验。目前对于ACC系统硬件在环仿真研究较少,本文首先基于 Simulink和 PreScan对ACC系统进行联合仿真,验证算法的可行性,然后生成代码并下载到电子控制单元(Electronic Control Unit, ECU),最后搭建基于dSPACE的硬件在环仿真平台,对设计的ACC控制器功能进行充分验证。
1 自适应巡航控制系统总体设计
本文采用上、下位控制器模式设计了ACC控制系统,图 1为自适应巡航控制系统总体结构。上位控制器负责接收自车车速和传感器检测到的车间相对距离与相对速度Δ,首先确定出期望车距、期望车间距误差Δ,然后通过状态切换策略决定进入速度控制模式或距离控制模式,最后LQR控制器根据Δ和Δ计算出期望加速度;下位控制器首先根据上位控制器得出的通过切换策略决定进入驱动或制动模式,进而由逆纵向动力学模型计算得到期望节气门开度和制动压力,最后将和传入车辆动力学模型,实现对车速和车距的自适应控制。

图1 自适应巡航控制系统总体结构
2 上位控制器的设计
2.1 安全车距的计算
安全车距决定了ACC系统的跟车距离,安全车距过小容易造成危险工况,安全车距过大容易被旁车道车辆换道插入,意味着跟车效率下降。因此,合理的安全车距能较好地适应多变的交通环境,保证安全性与跟车效率的平衡。
文献[6]提出了可变安全车距模型
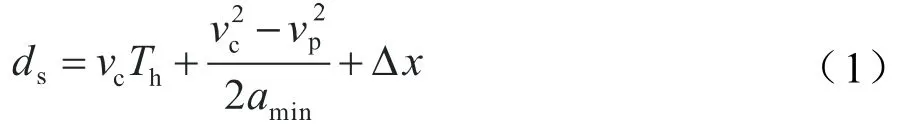
式中,为安全车距;为自车车速;为前车车速;为驾驶员和车辆的反应时间;为最小制动减速度;Δ为停车时两车安全车距。
具体到车辆,、、Δ均为定值,此处取 0.8 s,取 5.5 m/s,Δ取 3 m。行驶中防止前车因碰撞或其他因素导致车速突变为0,为保证自车安全性,取为0 m/s,化简式(1)得到

文献[5]通过车间反应距离判断自车对目标车辆作出反应的时机

式中,表示车间反应时距。

式中,为定速巡航车速;=2.5 s为设定的安全时距,式(3)可化简为

在速度控制模式下,当目标车辆在车间反应距离之外时(>),不受前车影响继续保持驾驶员设定的巡航车速行驶,当车距减小到车间反应距离之内时(≤),进入距离控制模式。
2.2 LQR控制器的设计
最优控制是在给定约束条件下,寻求使得系统性能指标达到极大(或极小)的反馈控制,ACC系统的设计是一个典型的最优控制问题。可以用状态空间方程来描述自车与前车之间的运动关系

式中,表示状态量;表示自车加速度是系统控制量;为目标车辆加速度;表示系统扰动量。由于rank[]=2满秩,因此通过控制系统可控准则判断上述系统具有完全可控性。
为了同时减少理想车距误差 Δ和相对车速Δ,引入线性二次优化性能指标函数

式中,为状态量权重系数;为控制量权重系数。

以性能指标函数最小为目标,最优控制为

式中,为状态反馈系数矩阵,=diag[,]。选择适当的权重系数,经比较不同值的控制效果最终选取1,6,18,计算得到0.235 7,0.542。为避免期望加速度过大超出正常范围或引起乘员不适,用饱和限制函数将限制在[0.4,0.3]的范围内。
2.3 状态切换策略
在真实行车环境中,在各种状态之间准确、平稳切换对汽车安全性和乘坐舒适性具有重要意义。上位控制器控制模式切换流程如图2所示。

图2 上位控制器模式切换策略
(1)首先判断是否检测到目标车辆,检测到目标车辆时==1;
(2)当没有检测到目标车辆(==0)或者前车在控制距离之外(>)或者前车车速大于设定的定速巡航车速(>)时,切换到速度控制模式,此时设置一虚拟车辆以设定巡航车速始终行驶在安全距离位置,即=,Δ=0,Δ=-;
(3)当检测到目标车辆(==1)且位于控制距离之内(≤)并且前车车速小于设定巡航车速(≤)时,切换回距离控制模式,此时上位控制器使用传感器实际检测到的前车信息,即目标车辆车速=+Δ,期望车距误差Δ=;
(4)经过状态切换层的决策,将速度差Δ和期望车间距误差Δ传入LQR控制器计算得到期望加速度。
3 逆纵向动力学模型
逆纵向动力学模型由驱动模块和制动模块组成,实际制动时应首先充分利用发动机和传动系统的倒拖、道路阻力和空气阻力,当减速度不满足制动需求时采用制动系统的制动力。在dSPACE车辆仿真模型(Automotive Simulation models,ASM)里进行带挡滑行试验,图 3为测出的对应不同车速下的滑行减速度。为避免自适应巡航系统在曲线附近位置频繁驱动、制动切换,破坏乘坐舒适性,设置厚度为(+)的缓冲层,缓冲层厚度过小不能解决频繁驱动、制动转换的问题,缓冲层厚度过大会引起系统响应滞后,进而发生控制超调。经过多次驱动、制动跟随试验,确定出为 0.05 m/s,为 0.1 m/s。

图3 带挡滑行减速度
上位控制器将解算得到的期望加速度输入下位控制器,在对应车速下,当≥+时进入驱动模式,当≤+时进入制动模式,当<<+时保持上一状态不变。
3.1 驱动控制
进入驱动模式后,通过上位控制器计算得出的期望加速度求解所需发动机扭矩,对应扭矩和发动机转速在逆发动机map图里确定节气门开度。
汽车行驶方程式为

式中,为地面制动力,由于驱动时无制动器制动力,因此地面制动力=0;为驱动力;为发动机扭矩;为变速器传动比;为主减速器传动比;为传动系机械效率;为液力变矩器涡轮转速;为发动机转速;(/)为液力变矩器转矩特性函数;为车轮滚动半径;为滚动阻力;为滚动阻力系数;为汽车质量;为坡道阻力;为道路坡度;为重力加速度;为空气阻力;为车辆迎风面积;为空气阻力系数;为空气密度;为汽车车速(m/s);为加速阻力;为旋转质量换算系数;为期望加速度。
联立式(12)—(17)得到

图4为根据dSPACE车辆动力学模型ASM中发动机脉谱图得到的发动机逆脉谱图。对应发动机转速和转矩,可以采用二维查表法确定相应的节气门开度:


图4 发动机逆动力学模型
3.2 制动控制
进入制动模式后,通过上位控制器计算得出的期望加速度求解所需制动力,然后由制动系统逆模型得到期望制动压力(单位bar),进而控制制动系统动作。
制动和驱动是分开动作的,此时节气门开度为0,驱动力为0,联立式(12)—(17)得到

当制动力不超出地面附着力时,可以认为制动力和制动压力近似呈线性关系,表示为

式中,为一系数,由式(20)(21)(22)得到

经过仿真试验,确定系数=220.34。
4 硬件在环测试
试验选用dSPACE公司的SCALEXIO实时仿真模拟器,dSPACE自带高自由度车辆动力学模型ASM。本文选取自适应巡航控制器ECU主控芯片型号为英飞凌SAK-TC234LP-32F200F AB。
图5为硬件在环仿真测试平台结构,采用PreScan搭建ACC典型测试场景,联合Simulink、dSPACE进行ECU硬件在环仿真测试。

图5 硬件在环仿真测试平台结构
在PreScan中创建测试工况,分别设计了目标车辆跟随、目标车辆切出、旁车低速切入三个试验。
4.1 目标车辆跟随试验
自车选用ASM中MidSizeCar,试验选取平直道路,设置自车初始位置(质心位置)在原点处,初始车速为 20 m/s,定速巡航车速设置为30 m/s。前车初始位置(质心位置)在50 m处,初始车速为25 m/s,匀速行驶900 m后以-1 m/s的减速度减速至 15 m/s,然后匀速行驶至仿真结束。试验1结果如图6—图8所示。
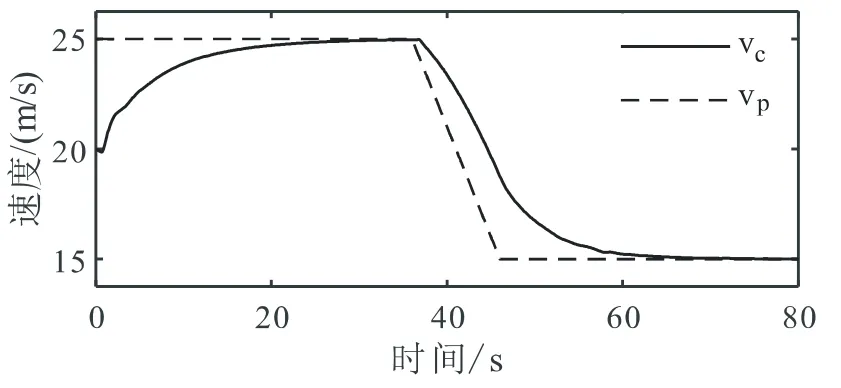
图6 试验1车速变化曲线

图7 试验1相对距离曲线

图8 试验1加速度变化曲线
图6可见,试验一开始自车识别出目标车辆,进入距离控制模式,自车车速逐渐从20 m/s提高到25 m/s。当前车突然以-1 m/s的加速度制动到15 m/s时,自车也能及时制动,速度跟随到15 m/s。
图7可见,加速跟随前车阶段,相对距离(自车最前端到前车尾部)逐渐从45.5 m稳定到80 m;前车减速后,将距离控制在35 m。
图8可见,在试验1工况下自车实际加速度变化趋势与理想加速度变化趋势基本相同,表明下位控制器具有较准确的执行能力。
4.2 目标车辆切出试验
自车初始位置在原点处,初始车速为15 m/s,定速巡航车速设置为30 m/s。前车初始位置在50 m处,初始车速为25 m/s,匀速行驶至600 m处,换道切出。试验2结果如图9—图11所示。

图9 试验2车速变化曲线

图10 试验2相对距离曲线

图11 试验2加速度变化曲线
由图 9可知,自车一开始锁定目标车辆,进入距离控制模式跟随前车,车速由15 m/s逐渐提高至25 m/s。前车行驶至600 m处换道切出,此时自车雷达检测不到目标车辆,模式切换至速度控制,车速逐渐提高到设定的巡航车速30 m/s。
由图10可知,加速跟随前车阶段,相对距离逐渐从45.5 m提高至80 m,前车变道切出后相对距离跳变为0,此时进入速度控制模式。
图11为加速度变化曲线。在试验2工况下自车实际加速度变化与理想加速度变化趋势基本相同。
4.3 旁车低速切入试验
设置自车初始位置在原点处,初始车速为20 m/s,定速巡航车速设置为30m/s。前车 1初始位置在80 m处,初始车速为28 m/s,前车1保持匀速行驶,在530 m处,前车2以15 m/s的车速紧急切入自车和前车1之间。试验 3结果如图12—图14所示。
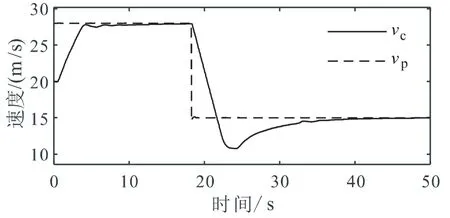
图12 试验3车速变化曲线

图13 试验3相对距离曲线

图14 试验3加速度变化曲线
由图12可知,自车一开始进入距离控制模式,车速跟随前车1至28 m/s,在530 m处,前车2紧急切入自车和前车1之间,自车将前车 2锁定为新的目标车辆,进入距离控制模式,减速跟随前车2至11 m/s后加速跟随,最终自车车速稳定在 15 m/s。
由图13可知,加速跟随阶段,相对距离从75.5 m逐渐稳定至95 m,前车2切入自车车道后相对距离跳变为32 m,采取制动后由于前车2车速小于自车车速,相对距离进一步缩小,自车减速至小于目标车辆车速后,相对距离逐渐增大,最终稳定在35 m。
由图14可知,在试验3工况下自车实际加速度变化趋势与理想加速度变化趋势基本相同。
5 结论
硬件在环仿真测试结果表明,当目标车辆速度变化、前车切出、旁车道车辆低速切入时,设计的基于最优控制的ACC系统可以适应多变的交通场景,及时做出正确的决策,在距离控制模式下可以保证安全跟车距离的同时稳定跟随前车,在速度控制模式下可以平稳地跟随设定巡航车速行驶。
