克拉玛依大风数值预报中的重力波拖曳方案应用研究

张涵斌 史永强 崔丽娜 杨程志

摘要 新疆克拉玛依地区位于背风坡，长期受翻山气流形成的局地大风影响。该地区日常大风预报业务主要依托克拉玛依气象局的精细化数值预报系统，为进一步完善该系统的预报效果，本文开展了重力波拖曳参数化方案应用试验，对比分析了三组试验方案：不开启重力波拖曳、只开启外层区域重力波拖曳以及两重嵌套设置下均开启重力波拖曳的结果。试验结果表明：在克拉玛依大风预报个例中，对于山区地形背风坡处的克拉玛依站，不启动重力波拖曳会导致风速偏大和起风时间较早;开启外层重力波拖曳方案可以延迟克拉玛依站起风时间，两重区域均开启可以进一步延迟该站的起风时间，使起风时间更接近实况;对于非山区地形背风坡处的站点，在内层开启重力波拖曳会导致一定的负效果;对内层区域的统计检验结果表明不开启重力波拖曳，会使地形复杂区域风场预报存在一定的正偏差，在外层开启重力波拖曳会使正偏差有一定改善，而两重嵌套均开启重力波拖曳方案会导致非地形陡峭区域的负偏差增加。综合全区域内大风预报检验结果表明，只在外层开启重力波拖曳会获得最小的误差和较好的预报效果。

关键词重力波拖曳;数值模式;参数化方案;大风预报;克拉玛依

随着现代高分辨数值预报技术的发展，模式中开始越来越多地考虑地形作用（王宇和黄思训，2018），该作用主要通过次网格参数化方案来实现，主要有“包络地形”方案（Wallace et al.，1983;Tibaldi，1986）以及“重力波拖曳”方案（Gravity Wave Drag，GWD;Phillips，1984;Palmer et al.，1986）。对于“重力波拖曳”参数化方案，其理论是当气流经过地形陡峭区时可能激发出地形重力波，从而产生水平动量耗散，数值模式中需要通过次网格参数化方案来描述这种地形引起的动量耗散过程，以使风场的模拟更加准确（McFarlane，1987;Baines and Manins，1989;Miller et al.，1989;程胡华，2017）。

Palmer et al.（1986）首次提出了欧洲中期预报中心全球模式的重力波拖曳方案，该方案主要描述了地形陡峭处的重力波激发机制，随后许多学者对重力波拖曳方案在模式中的应用进行了研究。Baines and Palmer（1990）利用非流线形动力学理论对重力波拖曳方案进行了进一步完善;Boer et al.（1984）首次实现了将重力波拖曳参数化引入到大尺度模式中;Kim and Arakawa（1995）对重力波拖曳方案进一步发展（KA95方案），并引入到WRF中尺度模式中，该方案主要描述了因地形方差引起的大气高层和低层重力波破碎将波能传播到下层并引起拖曳力增强的过程;Lott and Miller（1997）对原KA95方案进行了进一步改进，在重力波破碎模型的基础上引入了阻塞拖曳作用，并进行了一系列数值试验，结果表明新方案的预报技巧优于原方案。此后许多研究也表明，模式通过引入重力波拖曳方案可以更好地描述大尺度山脉对对流层动量收支的影响，从而改进预报效果（Kim and Doyle，2005;Hong et al.，2008;Sandu et al.，2013;Choi and Hong，2015）。

国内也开展了许多地形重力波拖曳参数化相关的研究，并阐述了重力波参数化方案的作用。周天军和钱永甫（1996）指出模式地形对于预报质量十分关键，需要在数值预报中考虑地形效应;钱永甫（2000）、刘华强和钱永甫（2001）在气候模式中针对重力波拖曳开展了试验，研究结果表明区域气候模拟中考虑地形重力波拖曳可以有效改善模拟结果;徐国强等（2010）通过全球天气模式研究了一次降水个例，指出引入地形重力波拖曳过程可以有效改善大气风场，对降水预报的落区有所改善。综合而言，国内针对重力波拖曳方案在中尺度数值模式中的研究较少，尚有待进一步开展。

新疆克拉玛依地区地处准噶尔盆地西北边，西有加依尔山，中部、东部为平坦戈壁，受特殊地理位置影响，大风盛行（辛渝等，2015），其中中部及南部主要受背风坡的强下坡风影响，春季大风较多，最大瞬时风速可达42.2 m/s。许多学者针对大地形影响下得气流过山及伴随的强下坡风进行了研究，指出由于背风波破碎而出现的湍流混合使得来自底层的重力内波在波破碎区产生反射进而导致下坡风暴的形成（Klemp and Lilly，1975;Lilly，1978;Clark and Peltier，1984;Saito，1993）;孫东霞等（2008）指出克拉玛依的背风坡地形是导致该地区强大风盛行的关键因素;卢冰等（2014）利用高分辨率WRF模式，重点阐述了克拉玛依地区背风坡风暴产生的机理，对冬季稳定层结及冷空气背景下重力波破碎导致的背风坡大风进行了细致分析，结果表明重力波效应是克拉玛依地区大风预报的关键。

目前克拉玛依市气象局业务运行数值天气预报系统，为克拉玛依地区大风天气的预报提供有效的业务支撑，但目前对克拉玛依地区大风模拟的强度和发生时间有待改进，本研究基于克拉玛依业务数值预报系统，探索了重力波拖曳方案在克拉玛依大风预报的应用效果。本研究不仅对克拉玛依当地大风预报的发展具有重要意义，也可为业务数值预报系统中大风预报改进提供新方法新思路，具有良好的应用前景。

1 资料和方法

1.1 克拉玛依精细化区域数值预报系统简介

克拉玛依市气象局发展的精细化区域数值预报系统基于美国环境预测中心（NCEP）和美国国家大气研究中心（NCAR）共同开发的非静力中尺度模式WRF V4.2版构建，模式区域设置为两重嵌套，其中外层D01水平分辨率15 km，模拟区域范围为中亚及新疆地区，共238×179个格点，垂直方向57层，覆盖新疆及中亚部分区域，两层区域单向嵌套无反馈;内层D02水平分辨率3 km，共295×200个格点，主要覆盖新疆北部区域（图1）。该系统每天从00时、12时（世界时，下同）起报两次，时间步长90 s，预报时效36 h，输出间隔1 h。系统采用NCEP全球预报场GFS资料（水平分辨率0.5°×0.5°，间隔6 h）作为初值驱动场和侧边界条件，物理过程参数化方案选取为：微物理过程采用Thompson方案（Thompson et al.，2004），边界层采用YSU方案（Hong et al.，2006），短波辐射和长波辐射采用RRTMG方案（Bae et al.，2016），D01积云方案采用New Tiedtke方案（Zhang et al.，2011），D02积云方案关闭。

1.2 重力波拖曳方案介绍

WRF次网格地形重力波拖曳参数化方案中，包含重力波破碎和阻塞拖曳两种作用（Kim and Doyle，2005），即在“gwd_opt=1”设置下，可开启两种参数化方案。

1.2.1 重力波破碎

WRF模式中的KA95方案不仅考虑了高层波破碎对重力波拖曳的影响，也考虑了因低层波破碎对下游重力波拖曳的影响：翻越地形陡峭区域的气流在参考层会产生相应的应力τ0，并激发垂直传播的重力波，重力波在不稳定环境中波破碎，此时拖曳力会受到一定损失，剩余的拖曳应力τ将在波破碎后继续扩散，使得下游也存在一定的拖曳应力。依据Kim and Arakawa（1995），参考层上的GWD为

其中：ρ为密度;N是Brunt-Vaisala频率;U是水平风速;Δx为模式的水平尺度;下标0代表是参考层，也就是重力波产生层;E为参考层上拖曳力的增强因子，用来增加受到低层波破碎或是抑制作用导致的拖曳力，主要受地形的非对称以及临界Froude数所影响;m代表网格内山的数量，G是渐进函数用来断定气流阻塞与否，因为经过修正，所以以m′、G′表示（钟水新等，2014）。

当重力波不满足饱和假设时，波能在上传过程中不损失，即上下层的GWD不变（τi=τi+1），据此获得上层波振幅（Palmer et al.，1986），并基于计算的上层波振幅求取局地修正后的Richardson数Ri。依据Lindzen（1981）的饱和假设，当满足Ri<Ric（饱和临界点的Richardson数）时，重力波在该层产生波破碎，部分能量损失使得τ减小，直至恢复到饱和临界点。当未达饱和条件时，重力波在该层不破碎，该层τ维持不变。

临界振幅hd的计算通过将Ri代入下式获得：

求得临界振幅后，计算该层剩余GWD：

获得GWD的垂直方向上所有层次（往上直到τi=0或模式层顶）的分布后，代入式（4）、（5）完成地形重力波拖曳对风场倾向的计算（钟水新等，2014）。

1.2.2 阻塞拖曳

拖曳参数化中的阻塞拖曳（Blocked-Layer Drag，BLD）是对KA95方案进行进一步扩展，公式基本上遵循Lott and Miller（1997）以及Scinocca and McFarlane（2000）的参数化研究，基于尺度分析获得，即如下拖曳形式：

其中：Δ2x为网格面积;Cd为一阶体积阻力系数;Δ⊥x是垂直于风向的网格长度;L⊥x是垂直于风向的次网格地形的宽度，近似为临界地形高度测得的地形宽度;hB为阻塞层高度，定义为：

地形的各向异性通过hB考虑，hB的计算包括Froude数Fr0，Frc（≈0.8）为临界Froude数，当Fr0>Frc时，该式应用到最低模式面以及地面层，并往上呈线性递减。

图2给出了克拉玛依数值模式D02范围内的地形分布以及WRF4.2中重力波拖曳参数化方案引起的地形拖曳应力作用，由图2a可以看出加依尔山-天山一带为地形陡峭区，其中克拉玛依位于加依尔山和准噶尔盆地交界处（46°N一线），由图2b可以看出次网格地形方差较大区域即为山区陡峭地形处，而地形重力波参数化方案引起的拖曳应力与地形大值区对应较好。

1.3 试验方案设计

为了验证重力波拖曳方案在克拉玛依精细化模式系统中的应用效果，基于重力波拖曳参数化方案开展了大风预报试验，重点针对重力波拖曳参数化方案在3 km区域内的表现进行分析。系统模式分辨率及范围设置均与1.1中介绍的一致。

设计了三种试验方案，方案一在D01和D02区域内关闭了GWD参数化方案，其余设置与1.1中介绍的方案一致，称为GWD00方案;方案二在D01区域开启GWD参数化方案，D02区域关闭GWD方案，称为GWD10方案，方案三在D01和D02范围内均开启重力波拖曳，称为GWD11方案，如表1所示。开展了2021年2月1个月的连续试验，其中以2月24日—25日发生在克拉玛依的大风天气过程为重点研究个例。

2 试验结果分析

2.1 大风个例分析

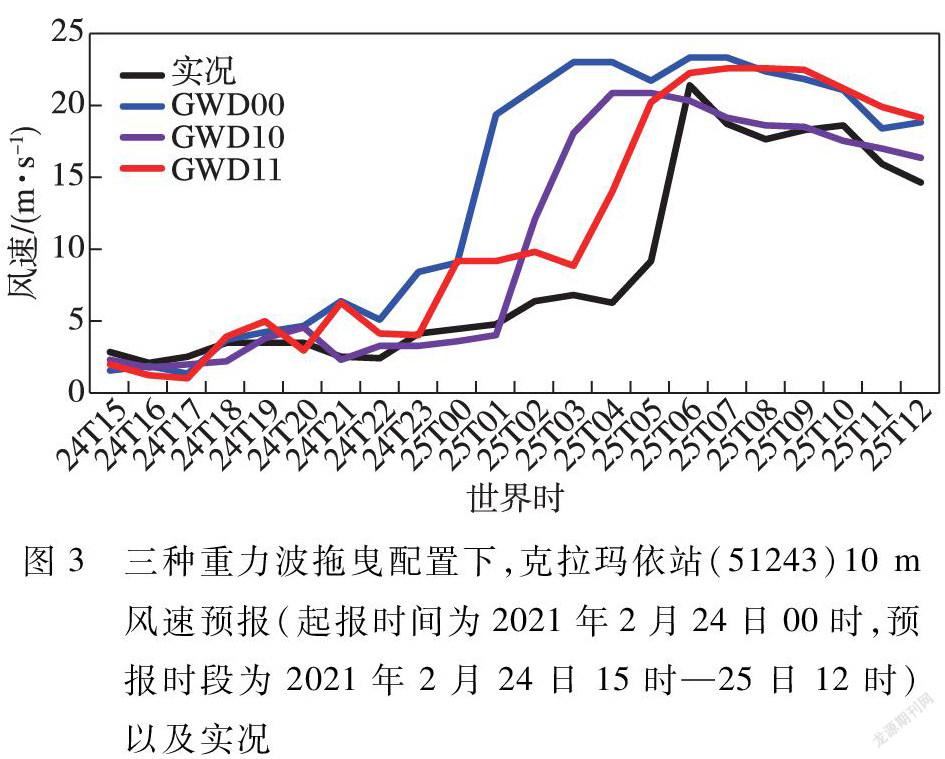
2021年2月24日，受極涡分裂短波东移影响，克拉玛依城区发生了一次大风天气，25日06时，在冷空气南下影响下，克拉玛依城区起风，逐小时最大风速可达21.3 m/s，已达到大风级别（近地面层平均风速17.2～20.7 m/s）。图3给出了三种重力波拖曳方案配置下，克拉玛依站（51243）10 m风速预报和实况，预报时段为2021年2月24日15—25日12时。可以看出对于实况，25日04时之前风速仅为5 m/s，25日06时整点风速增加到21.3 m/s;对于GWD00方案，其起风时间明显过早，25日01时已达20 m/s左右，起风时间相对于实况提前了5 h，此后数小时基本上处于20 m/s以上，个别时间可达24 m/s，在实况起风时刻06时之后的风速大小也明显强于实况;对于GWD10，大风起风时间相对于实况依然偏早，在03时其风速也达18 m/s，比实况提前3 h左右，但在06时之后与实况风速十分接近;对于GWD11设置，由于D02加入了重力波拖曳，起风时间相对于GWD10进一步延后，风速增加到20 m/s的时间为25日05时，但06时之后风速相对于实况也偏高。06时之后，不管是实况还是三种方案预报，均呈现明显减小的趋势。综合以上结果，D01增加GWD可以有效改善背风坡山脚处克拉玛依站的起风时间和大风持续时段的风速预报，而D02增加GWD可以进一步改善大风的起风时间。

图4给出了三种方案不同预报时效（19～30 h）对克拉玛依市区风速预报的分布，可以看出模式预报的大风不断越过加依尔山背风坡侵入克拉玛依城区，但是三种方案风速大值区进入的时间明显不同，GWD00方案在21～24 h预报时效的风速大值即位于加依尔山下坡处，侵入克拉玛依西部的克拉玛依主城区，在27～30 h时段风速也明显较强，在27～30 h时段可以发现在克拉玛依西北部存在明显的大值中心，量级可达24 m/s以上;GWD10方案在21～24 h风速大值区也影响到了克拉玛依城区，在27～30 h时段风速也明显较强，风速大值中心可达24 m/s以上，只是大值范围略小于GWD00方案;GWD11方案相对于前两种方案，风速明显减弱，27 h预报时效之前，风速大值区基本没有影响到克拉玛依城区，且量级较小，直到28 h之后，克拉玛依城区预报才可达到18 m/s以上，说明两重嵌套均开启重力波拖曳，可以显著降低风速预报，从而影响大风进入克拉玛依城区的时间和量级。

卢冰等（2014）对克拉玛依强下坡风形成机制的分析中指出，克拉玛依上游地区中高层到低层存在强西风气流并在低层伴有冷平流的情况下，随着风速不断增大，气流能够翻越加依尔山在背风坡形成重力波，重力波能够往上传播影响到高空气流并形成波破碎，破碎区湍流运动可导致上层能量向下传播。为进一步研究本次大风个例中重力波拖曳方案对克拉玛依翻山气流大风降温的影响，给出了27 h预报时效的2021年2月25日03时GWD00和GWD10方案大风进入城区时刻沿加依尔山至克拉玛依市区一线46°N的风向和位温预报垂直剖面，如图5所示。从三个方案的剖面可以看出，首先对于高空风场GWD00方案（图5a）加依尔山上空6 km处基本处于较强的西风气流之中，垂直风切变较小，说明重力波传播基本已经结束;对于GWD10方案（图5b），受外层重力波拖曳方案引起的风场变化影响，地形背风坡上空存在较明显的垂直运动，5 km以上存在上升气流;GWD11方案（图5c）在5 km以上垂直运动更为剧烈，具有明顯的垂直向上分量。5 km以下，所有方案中翻山气流均向山麓推进，其中GWD00气流翻山后在近地面以西风分量为主，冷空气快速进入，如284 K等位温线明显向山脚延伸;GWD10受重力波破碎导致能量向下传播影响，在5 km高度以下具有明显的下沉气流特征，山脚下克拉玛依站风速水平分量有所减弱，而垂直分量有所增加，冷空气也明显向山脚下延申;而GWD11方案翻山气流水平风速明显小于GWD00和GWD10，风的垂直分量更为显著。以上分析说明当模式内外层均未加入重力波拖曳作用，背风坡上空的次网格湍流垂直扩散未考虑，背风坡处的水平风速偏强;外层加入重力波拖曳后，重力波垂直湍流扩散显著，削弱水平风速项，导致下坡风的延迟和减弱;在内层区域开启重力波拖曳的方案，进一步延缓了翻山气流的水平风速，并延迟了冷平流带来的局地降温。

利用克拉玛依附近14个区域自动站实况资料对克拉玛依市及其周边的站点预报进行检验，计算27 h预报时效（对应时刻为25日03时）的区域内各站点上的预报偏差分布以及区域平均的平均误差（Mean Error，ME，或称之为偏差）以及平均绝对误差 （Absolute Mean Error，AME），如图6所示。对于GWD00（图6a），加依尔山山脚下的克拉玛依站具有明显的风速正偏差，可达10 m/s以上，其他站的预报偏差有正有负，范围内总体的ME为2.19 m/s，AME为3.45 m/s，表现出明显的正偏差;对于GWD10方案（图6b），可以看出克拉玛依站风速正偏差依然为10 m/s以上范围，而总体上的偏差有一定减少，ME达到1.57 m/s;GWD11方案，克拉玛依站预报效果进一步改善，正偏差降到2～5 m/s范围内，总体偏差特征ME为-0.43 m/s，负偏差站点有所增多。

总体上看GWD10整体上改善了GWD00的正偏差，但对克拉玛依站的起风时间预报依然过早;而GWD11方案进一步改善了克拉玛依站及其附近站点的正偏差，但带来了一定的负偏差。

2.2 检验结果

对批量试验时段内的预报结果进行评分统计，进一步定性和定量分析不同重力波拖曳设置下的模式预报效果。

首先，定性分析重力波拖曳方案对预报效果的影响，本节的实况分析场采用检验时刻对应的WRF初始分析场（由GFS初始场驱动并同化了相应的探空和地面站观测资料）。图7给出了批量试验时段内统计平均的24 h预报时效的D02区域内纬向U风场预报与预报时刻对应的分析场之差沿85°E剖面，该剖面位置为加依尔山背风坡。

从图7a可知GWD00方案的U风预报在加依尔山背风坡相对于分析场具有明显的正偏差，这种正偏差从高空200 hPa一直延续到地面背风坡上，说明无GWD作用下，山区地形上空纬向风速具有显著偏大特征;在D01方案中开启GWD，即GWD10方案，其对D02纬向风速也有显著影响，如200 hPa左右正偏差得到了显著削弱，甚至出现了一定的负偏差，对于350 hPa以下，46°～47.4°N范围内，部分区域偏差已经降低到-2～2 m/s;当D02开启GWD方案后，即GWD11，可以看出，对于高空风正偏差区域范围进一步缩小，而负偏差特征进一步增大，需要注意的是，GWD11设置下对于背风坡近地面处的风速偏差确实有明显改善，如750 hPa高度的山坡区域风速正偏差仅为2 m/s左右，显著小于GWD00及GWD10方案，而对于无地形区域的近地面及高空风场，GWD11相对于前两种方案显著增加了风速负偏差，这也说明开启D02的重力波拖曳作用对全场预报效果具有较大的不一致性。

为了检验三种方案统计预报效果，计算了三种方案试验时段内D02区域不同要素统计平均的均方根误差（RMSE）以及偏差（BIAS），包括2 m高度气温（T2m）、10 m高度纬向风（U10m）以及10 m高度径向风（V10m），实况采用D02区域内所有地面自动站，间隔6 h。图8给出了三种方案36 h预报时效内D02区域地面要素预报的RMSE和BIAS的演变特征，可以看出，对于RMSE，不管是温度预报还是风场预报，GWD10在各个预报时效均能够获得最低的RMSE，而GWD11方案对不同要素预报的RMSE均较大，GWD00方案居中，如对于U风场的24 h预报，GWD00误差为3.25 m/s，GWD10为2.86 m/s，GWD11为3.35 m/s。从BIAS可以看出，对于风场预报（图8b和图8c），GWD00表现出一定的正偏差，尤其是12～30 h预报时效较为明显，如18 h预报时效的BIAS为0.23 m/s;GWD10相对于GWD00风场预报的正偏差有一定减小，18 h预报时效的BIAS为-0.16 m/s;而GWD11方案相对于GWD10方案的风场有了明显的负偏差，18 h预报时效的BIAS为-0.47 m/s，这也与上文中的定性分析结论相一致。以上分析说明整体上GWD10设置下的预报效果较好，而GWD11设置下会对风场存在“过度矫正”问题，引起偏差增大。

图9给出了试验时段内探空观测检验的12、24、36 h三个预报时效平均的RMSE垂直分布，其他非整点时次由于探空资料较少，因此不计入统计。首先可以看出对于U风预报（图9a），三种方案各个层次误差量级不同，其中在400 hPa误差最大，GWD00方案误差达到6.6 m/s，而GWD10和GWD11方案误差为5.5 m/s左右，显著小于GWD00方案，对于模式低层，GWD10的误差相对也较小，如850 hPa误差为1.63 m/s，小于GWD00的2.17 m/s和GWD11的1.87 m/s，对于另外两个要素，两种重力波方案相对于不加入重力波方案也显示出一定的优势，综合而言GWD10在不同等压面均可获得更好的要素预报，尤其是对于边界层而言，GWD10的预报可以获得更好的热动力状况，从而有效改善克拉玛依城区翻山下坡风的预报。

综上所述，在外层区域D01开启重力波拖曳，内层区域D02关闭重力波拖曳，可以获得较好的综合效果。虽然对于克拉玛依单站预报，D02也开启重力波拖曳有可能会获得较好的效果，但是会影响其他非地形陡峭区域的风场预报。而D01和D02均不开启重力波拖曳，会使风场存在固有的系统性正偏差，因此从日常需求来看，在D01开启重力波拖曳是比较合理的设置。

3 结论和讨论

基于克拉玛依数值系统开展了冬季大风预报试验，对比了不同重力波拖曳方案设置即两重嵌套均关闭重力波拖曳（GWD00）、仅开启D01重力波拖曳（GWD10）和两重嵌套均关闭重力波拖曳（GWD11）三组方案对克拉玛依大风预报的效果，重点分析了2月25日大风预报个例，并通过地面要素检验指标对三种方案的预报效果进行综合评估，得出以下结论：

1）对于克拉玛依冬季稳定层结下的一次大风个例，三种方案的起风时间各不相同，其中GWD00方案起风过早，大风延续时间最长，大风量级相比实况有正偏差;GWD10方案起风时间有所延迟，且大风量级与实况最接近;GWD11方案起风时间最接近实况。说明本次个例，重力波拖曳可以有效减弱地形陡峭区域大风预报正偏差。

2）对克拉玛依周边单站预报进行分析，表明虽然山区背风坡的克拉玛依站在两重嵌套中引入重力波拖曳可以有效减小近地面风场误差，但是对其他区域站点预报则带来一定的负效果，说明两重嵌套均开启重力波拖曳并不能全面改善预报区域内的效果。

3）进行了批量试验检验，定性分析表明：未开启重力波拖曳的情况下会在山区地形处存在明显正偏差，在外层区域开启重力波拖曳则会在平流层至地面均有效减少风场预报正偏差，而内外层均开启重力波拖曳，虽然会有效减小背风坡近地面风速正偏差，但会在非山地区域增加负偏差;通过统计检验发现相对于未開启重力波拖曳的设置，在外层开启重力波拖曳可以有效降低不同预报时效地面要素均方根误差，但是进一步开启内层区域的重力波拖曳，会导致均方根误差有所增加，主要是由于开启外层重力波拖曳增加了一定的负偏差。

以上结论表明WRF中重力波拖曳方案，由于包含重力波破碎和阻塞拖曳的模型均针对大尺度山脉对对流层动量收支的影响，因此在外层粗分辨率区域开启重力波拖曳，内层关闭重力波拖曳时，区域整体预报具有较好的效果，但对于克拉玛依这种处于山区背风坡位置的站点，开启内层重力波拖曳可获得更好的预报效果（而其他站点预报效果会变差）。如果既提高背风坡站点预报，又保持其他非地形区域预报技巧，则需要引入针对高分辨率地形网格的重力波拖曳效应，充分描述稳定边界层内的缺失拖曳作用。Steeneveld et al.（2008）提出相对较浅的稳定边界层内的拖曳作用可以通过小尺度地形来获取，并形成了稳定边界层重力波拖曳方案GWDSBL，该方案已初步耦合到WRF V4.3中（Tsiringakis et al.，2017）。此种针对稳定边界层的重力波拖曳方案在克拉玛依高分辨率数值预报系统中的表现如何，未来需要进一步开展试验。

参考文献（References）

Bae S Y，Hong S Y，Lim K S S，2016.Coupling WRF double-moment 6-class microphysics schemes to RRTMG radiation scheme in weather research forecasting model[J].Adv Meteorol，2016：1-11.doi：10.1155/2016/5070154.

Baines P G，Manins P C，1989.The principles of laboratory modeling of stratified atmospheric flows over complex terrain[J].J Appl Meteor，28（11）：1213-1225.doi：10.1175/1520-0450（1989）028<1213：tpolmo>2.0.co;2.

Baines P G，Palmer，T N，1990.Rationale for a new physically based parametrization of sub-grid scale orographic effects[J].Ecmwf Tech.doi：10.21957/h4h36b3u.

Boer G J，McFarlane N A，Laprise R，et al.，1984.The Canadian Climate Centre spectral atmospheric general circulation model[J].Atmosphere-Ocean，22（4）：397-429.doi：10.1080/07055900.1984.9649208.

程胡华，2017.不同扰动场对大气重力波参数结果影响的初步探讨[J].大气科学学报，40（3）：401-411. Cheng H H，2017.A preliminary investigation on the atmospheric gravity wave parameters obtained from different disturbance fields[J].Trans Atmos Sci，40（3）：401-411.doi：10.13878/j.cnki.dqkxxb.20160504002.（in Chinese）.

Clark T L，Peltier W R，1984.Critical level reflection and the resonant growth of nonlinear mountain waves[J].J Atmos Sci，41（21）：3122-3134.doi：10.1175/1520-0469（1984）041<3122：clratr>2.0.co;2.

Choi H J，Hong S Y，2015.An updated subgrid orographic parameterization for global atmospheric forecast models[J].J Geophys Res：Atmos，120（24）：12445-12457.doi：10.1002/2015JD024230.

Hong S Y，Noh Y，Dudhia J，2006.A new vertical diffusion package with an explicit treatment of entrainment processes[J].Mon Wea Rev，134（9）：2318-2341.doi：10.1175/mwr3199.1.

Hong S Y，Choi J，Chang E C，et al.，2008.Lower-tropospheric enhancement of gravity wave drag in a global spectral atmospheric forecast model[J].Wea Forecasting，23（3）：523-531.doi：10.1175/2007waf2007030.1.

Kim Y J，Arakawa A，1995.Improvement of orographic gravity wave parameterization using a mesoscale gravity wave model[J].J Atmos Sci，52（11）：1875-1902.doi：10.1175/1520-0469（1995）052<1875：ioogwp>2.0.co;2.

Kim Y J，Doyle J D，2005.Extension of an orographic-drag parametrization scheme to incorporate orographic anisotropy and flow blocking[J].Quart J Roy Meteor Soc，131（609）：1893-1921.doi：10.1256/qj.04.160.

Klemp J B，Lilly D R，1975.The dynamics of wave-induced downslope winds[J].J Atmos Sci，32（2）：320-339.doi：10.1175/1520-0469（1975）032<0320：tdowid>2.0.co;2.

Lott F，Miller M J，1997.A new subgrid-scale orographic drag parametrization：Its formulation and testing[J].Quart J Roy Meteor Soc，123（537）：101-127.doi：10.1002/qj.49712353704.

Lilly D K，1978.A severe downslope windstorm and aircraft turbulence event induced by a mountain wave[J].J Atmos Sci，35（1）：59-77.doi：10.1175/1520-0469（1978）035<0059：asdwaa>2.0.co;2.

Lindzen R S，1981.Turbulence and stress owing to gravity wave and tidal breakdown[J].J Geophys Res：Oceans，86（C10）：9707-9714.doi：10.1029/JC086iC10p09707.

劉华强，钱永甫，2001.包络地形和重力波拖曳对区域气候模拟效果的影响[J].大气科学，25（2）：209-220. Liu H Q，Qian Y F，2001.Effects of envelope orography and gravity wave drag parameterization on regional climate simulations[J].Chin J Atmos Sci，25（2）：209-220.（in Chinese）.

卢冰，史永强，王光辉，等，2014.新疆克拉玛依强下坡风暴的机理研究[J].气象学报，72（6）：1218-1230. Lu B，Shi Y Q，Wang G H，et al.，2014.Numerical study of severe downslope winds at Kelamayi，Xinjiang[J].Acta Meteorol Sin，72（6）：1218-1230.（in Chinese）.

Miller M J，Palmer T N，Swinbank R，1989.Parametrization and influence of subgridscale orography in general circulation and numerical weather prediction models[J].Meteor Atmos Phys，40（1/2/3）：84-109.doi：10.1007/BF01027469.

McFarlane N A，1987.The effect of orographically excited gravity wave drag on the general circulation of the lower stratosphere and troposphere[J].J Atmos Sci，44（14）：1775-1800.doi：10.1175/1520-0469（1987）044<1775：teooeg>2.0.co;2.

Palmer T N，Shutts G J，Swinbank R，1986.Alleviation of a systematic westerly bias in general circulation and numerical weather prediction models through an orographic gravity wave drag parametrization[J].Quart J Roy Meteor Soc，112（474）：1001-1039.doi：10.1002/qj.49711247406.

Phillips D S，1984.Analytical surface pressure and drag for linear hydrostatic flow over three-dimensional elliptical mountains[J].J Atmos Sci，41（6）：1073-1084.doi：10.1175/1520-0469（1984）041<1073：aspadf>2.0.co;2.

钱永甫，2000.包络地形和重力波拖曳对气候模拟效果的影响[J].应用气象学报，11（1）：13-20. Qian Y F，2000.Effects of envelope orography and gravity wave drag on performance of climate modeling[J].J Appl Meteor Sci，11（1）：13-20.doi：10.3969/j.issn.1001-7313.2000.01.002.（in Chinese）.

Saito K，1993.A numerical study of the local downslope wind “yamaji-kaze” in Japan[J].Journal Meteorological Society Japan，71（2）：247-272.doi：10.2151/jmsj1965.71.2_247.

Sandu I，Beljaars A，Bechtold P，et al.，2013.Why is it so difficult to represent stably stratified conditions in numerical weather prediction （NWP） models？[J].J Adv Modeling Earth Syst，5（2）：117-133.doi：10.1002/jame.20013.

Scinocca J F，McFarlane N A，2000.The parametrization of drag induced by stratified flow over anisotropic orography[J].Quart J Roy Meteor Soc，126（568）：2353-2393.doi：10.1002/qj.49712656802.

Steeneveld G J，Holtslag A A M，Nappo C J，et al.，2008.Exploring the possible role of small-scale terrain drag on stable boundary layers over land[J].J Appl Meteorol Climatol，47（10）：2518-2530.doi：10.1175/2008jamc1816.1.

Tsiringakis A，Steeneveld G J，Holtslag A A M，2017.Small-scale orographic gravity wave drag in stable boundary layers and its impact on synoptic systems and near-surface meteorology[J].Quart J Roy Meteor Soc，143（704）：1504-1516.doi：10.1002/qj.3021.

孫东霞，谢小红，郭晓静，2008.克拉玛依特强大风的气候特征及天气分析与预报[J].沙漠与绿洲气象，2（4）：18-21. Sun D X，Xie X H，Guo X J，2008.The climatic characteristics of the extreme strong wind in Kelamayi and its weather analysis and forecast[J].Desert Oasis Meteorol，2（4）：18-21.doi：10.3969/j.issn.1002-0799.2008.04.003.（in Chinese）.

Tibaldi S，1986.Envelope orography and maintenance of the quasi-stationary circulation in the ECMWF global models[J].Adv Geophys，29：339-374.doi：10.1016/S0065-2687（08）60045-X.

Thompson G，Rasmussen R M，Manning K，2004.Explicit forecasts of winter precipitation using an improved bulk microphysics scheme.part Ⅰ：description and sensitivity analysis[J].Mon Wea Rev，132（2）：519-542.doi：10.1175/1520-0493（2004）132<0519：efowpu>2.0.co;2.

Wallace J M，Tibaldi S，Simmons A J，1983.Reduction of systematic forecast errors in the ECMWF model through the introduction of an envelope orography[J].Quart J Roy Meteor Soc，109（462）：683-717.doi：10.1002/qj.49710946202.

王宇，黄思训，2018.几种特殊地形对气流运动影响的解析研究[J].大气科学学报，41（6）：743-752. Wang Y，Huang S X，2018.Analytical study of the influence of several special topographies on airflow movement[J].Trans Atmos Sci，41（6）：743-752.doi：10.13878/j.cnki.dqkxxb.20180114001.（in Chinese）.

辛渝，周颖真，宋丽莉，等，2015.新疆风区下垫面动力学粗糙度估测值与模式定义值的对比[J].大气科学学报，38（6）：811-818. Xin Y，Zhou Y Z，Song L L，et al.，2015.Aerodynamic roughness comparison between the estimated based on masts and the defined in model over Xinjiang wind areas[J].Trans Atmos Sci，38（6）：811-818.doi：10.13878/j.cnki.dqkxxb.20141125002.（in Chinese）.

徐國强，杨学胜，黄丽萍，等，2010.GRAPES中地形重力波拖曳物理过程的引进和应用试验[J].气象学报，68（5）：631-639. Xu G Q，Yang X S，Huang L P，et al.，2010.Introducing and application testing of the orographic gravity wave drag parameterization physics in the GRAPES[J].Acta Meteorol Sin，68（5）：631-639.（in Chinese）.

Zhang C X，Wang Y Q，Hamilton K，2011.Improved representation of boundary layer clouds over the southeast Pacific in ARW-WRF using a modified tiedtke cumulus parameterization scheme[J].Mon Wea Rev，139（11）：3489-3513.doi：10.1175/mwr-d-10-05091.1.

钟水新，陈子通，戴光丰，等，2014.地形重力波拖曳参数化对热带气旋强度和路径预报影响的研究[J].大气科学，38（2）：273-284. Zhong S X，Chen Z T，Dai G F，et al.，2014.Impacts of orographic gravity wave drag parameterization on typhoon intensity and path forecasting[J].Chin J Atmos Sci，38（2）：273-284.doi：10.3878/j.issn.1006-9895.2013.13131.（in Chinese）.

周天军，钱永甫，1996.地形效应影响数值预报结果的试验研究[J].大气科学，20（4）：452-462. Zhou T J，Qian Y F，1996.An experimental study on the effects of topography on numerical prediction[J].Sci Atmos Sin，20（4）：452-462.（in Chinese）.

（责任编辑：袁东敏）