长江水道事故风险预测模型优化
2022-04-02丁振国张树奎胡甚平
丁振国 张树奎 胡甚平





摘要:针对支持向量机(support vector machine, SVM)模型在水上交通风险预测中由于其变量较多而导致的计算过程复杂、实用性不强的问题,运用随机森林模型对变量进行重要度排序,利用筛选后的变量构建新的SVM模型。将新模型的分类正确率和可转移性测试结果与原模型的进行比较。结果表明:新模型比原模型的分类正确率提高4.12个百分点;在可转移性测试中新模型分类正确率仍处于较高水平,而且误报率降低2.40个百分点。研究表明新模型计算相对简单,预测效果更优,而且具有普适性特征。
关键词:
长江水道; 风险预测; 随机森林; 支持向量机; 机器学习
中图分类号: U697
文献标志码: A
Optimization of accident risk prediction model for Yangtze River waterway
DING Zhenguo1, ZHANG Shukui1, HU Shenping2
(1. Navigation College, Jiangsu Maritime Institute, Nanjing 211170, China;
2. Merchant Marine College, Shanghai Maritime University, Shanghai 201306, China)
Abstract:
In view of the complicated calculation process and low practicability due to a large number of variables of the support vector machine (SVM) model in the prediction of water traffic risk, the random forest model is used to rank the importance of variables, and the filtered variables are used to construct a new SVM model. The classification accuracy and the transferability test result of the new model are compared with those of the original model. The results show that: the classification accuracy of the new model is 4.12 percentage points higher than that of the original model; in the transferability test, the classification accuracy of the new model is still at a high level, the false alarm rate is reduced by 2.40 percentage points. The research shows that the new model is of relatively simple calculation, better prediction effect, and universal applicability features.
Key words:
Yangtze River waterway; risk prediction; random forest; support vector machine; machine learning
0 引 言
长江下游水道,船舶往来密集,交通流量大,船舶交通事故频发。据中华人民共和国江苏海事局2019年发展报告统计,长江江苏段2016年、2017年、2018年分别发生水上交通事故28起、18起、19起。交通事故造成了大量人员伤亡和财产损失,甚至是严重的环境污染。随着绿色、健康发展理念的贯彻实施,水上交通安全问题受到越来越多的关注,这给相关管理部门提出了更高的要求。
水上交通安全管理的前提是掌握交通事故发生的机理,从而采取有针对性的措施。目前关于水上交通事故预测的研究成果较多,研究方法主要有灰色关联分析法[1]、贝叶斯网络[2]、反向传播(back propagation,BP)神经网络[3]、组合预测方法等[4]。这些方法都能够较好地预测船舶安全状况,但也各有缺点:对于非光滑的历史事故数据序列,灰色关联分析法预测精度较低,且需要人为选取适当的模型参数值[5];贝叶斯网络在模型结构学习时需要大量样本数据才能发挥其优势,当样本数据较少时其预测误差较大[6];BP神经网络需要通过不断调整相关参数来确定最优隐含层节点数、学习速率和最大误差值,计算负担较重[7];组合预测方法虽然可以克服单一模型的不足,但是由于各模型建立的条件不同,在组合预测时各条件易相互制约,导致某一模型优势得不到发挥,影响预测效果[8]。近年来,支持向量机(support vector machine, SVM)被引入水上交通研究领域,取得了较好的效果,但是采用该方法预测时需要选取的交通安全影响因素多,计算过程較为复杂,实用性不强[9]。随机森林(random forest,RF)模型可以从众多影响因素中筛选出重要因素,从而降低后续的计算复杂度[10]。
本文以长江下游水道为研究对象,首先运用RF模型对影响船舶航行安全的因素进行筛选,然后运用筛选后的变量构建新的SVM模型,最后利用长江下游历史数据验证新模型的有效性和普遍适用性,并与原模型预测结果进行比较。
1 问题提出
船舶通航安全影响因素众多,在系统综合评价时,选择的影响因素并非越多越好,但也不是越少越好。因素过多则存在重复性,且计算过程复杂;因素过少则缺乏足够的代表性,会产生片面性。因此,科学合理地筛选船舶通航安全影响因素非常重要[11]。
船舶通航安全风险预测模型的优劣直接影响到预测结果的准确性,进而影响管理者决策的正确性。对预测模型效果进行评价,能够反映出所建模型的优劣。
1.1 通航安全影响因素选取
根据已有研究成果,结合长江下游水道特点[12],选取13个影响船舶通航安全的主要因素,分别为:航道长度、航道弯曲率、航道深度、主航道宽度、能见度、大风、交通流密度、船舶速度差、最小会遇时间、船舶纵向加速度、船舶横向加速度、“船舶纵向加速度+最小会遇时间”及“船舶横向加速度+最小会遇时间”。
1.2 水上交通风险预测方法的评价指标
研究表明,分类正确率Aca、漏报率Rfn和误报率Rfp这3个指标能够较好地评价预测模型的优劣[13]。本文利用这3个指标对模型的预测效果进行评价。针对该二分类问题,令实际的交通事故被预测为正确的数量和被预测为错误的数量分别为YT和YF,实际的非交通事故被预测为错误的数量和被预测为正确的数量分别为NF和NT。因此,Aca、Rfn和Rfp分别计算如下:
2 水上交通风险预测模型
2.1 RF模型
RF模型是由多棵分类回归树(classification and regression tree, CART)构成的组合分类模型,在识别变量重要性方面效果较好,是常用的统计算法之一。RF模型的基本原理为:利用自助法重采样技术从初始样本集G={(uq,vq),q=1,2,…,n}中任意抽取s个样本组成一个训练样本集Gs,利用Gs构建一棵CART,CART从全部变量T中任意选择t个变量(t≤T)分割节点;重复上述步骤s次,建立一个由s棵树构成的RF模型。将测试数据输入该模型中进行分类投票,并计算结果。
因为采用的是有放回采样,所以会存在样本被重复采样的问题,当然也会存在样本未被采样的问题。未被采样的数据称为袋外(out-of-bag, OOB)数据,未被采样的数据集记为GOOB。利用由s棵树构成的RF模型对GOOB进行分类,并统计分类正确次数;然后改变自变量uq的值,再利用uq和RF模型对GOOB进行分类,并统计分类正确次数;最后利用两次分类正确次数,计算uq改变后分类正确率的下降值,得到uq的重要程度。
2.2 SVM模型
SVM模型是一种用于解决分类问题的非参数方法,广泛应用于水上交通领域,对于预测交通流量、交通事故等具有优势[14]。SVM的建模思想为:给定一个二分类的特定数据集,若该数据集具有N个变量,则N个变量构成一个N维空间X=(x1,x2,…,xN),即在N维空间内存在一个N-1维超平面,其中有一个最优解可以有效区分二分类数据。建模过程如下:步骤1 给定一个特定训练数据集,X为其输入空间,xi为一输入向量,yi为对应的输出,Y={yi}={-1,1}。当yi=-1时,xi为负例;当yi=1时,xi为正例。
步骤2 构建分离超平面方程,用来确定输入向量是负例还是正例:
3 算例应用
3.1 数据准备
以长江江苏段水域为研究对象,研究数据来自船舶交通服务(vessel traffic service,VTS)中心。长江下游是我国最重要的黄金水道,船舶流量大,交通事故频发,可采集到的样本较为丰富。水道交通状态分为可能发生事故和不会发生事故两类,因此信息采集包括发生事故时的水道状态信息和未发生事故时的水道状态信息。非事故样本数据采集需要在不同的水道状态下随机选择。信息采集主要通过以下方法完成:事故样本数据和非事故样本数据由VTS中心提供,其中非事故样本数据包括交通险情、一般以下等级事故及交通正常等,船舶交通密度、船舶航速等数据主要来自岸基雷达、闭路电视(closed-circuit television,CCTV)、船舶检测器、船舶自动识别系统(automatic identification system,AIS)等设备。
信息采集水道为尹公洲水道,采集时间为2010年4月至2020年3月,采集样本共1 145个,其中事故样本116个,非事故样本1 029个,每个样本均具有详细的变量数据。
將116个事故样本和1 029个非事故样本分别按照约4∶1的比例随机划分成训练集和测试集。由于样本数量越充足训练效果越好[15],所以将事故样本集中训练集的数据重复输入9次,使得事故样本的数据量与非事故样本的数据量之比接近1∶1,以保证达到相同的训练效果。
3.2 模型应用
3.2.1 模型参数确定
利用模型预测前,需要确定参数C、η、p的值。根据历史经验数据,3个参数的取值范围分别为C∈[0.01,10],η∈[0.01,10],p∈[1,3],具体数值需对不同参数组合下的模型预测结果进行比较并结合十重交叉验证法最终确定。利用确定的参数值构建SVM分类器。本文最终确定C、η、p的值为分别为0.5、1、1。
3.2.2 RF模型计算
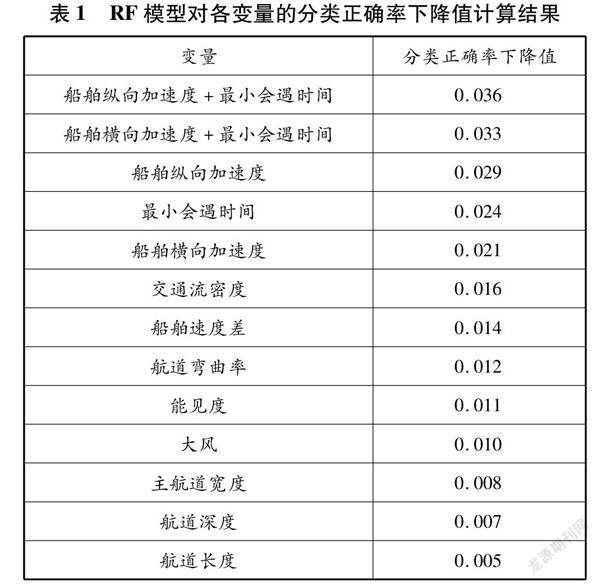
通过计算机编程,利用MATLAB实现RF模型的计算。将13个主要变量输入已经编写好的程序中,RF模型对各变量的分类正确率下降值计算结果见表1。
从表1可知,分类正确率的下降值大于0.020的有5个变量,小于0.020的有8个变量。为证明重要变量的作用,考虑预测正确率的要求,选取下降值大于0.020的5个变量作为SVM模型的输入变量,以检验SVM模型的预测效果。
对训练集和测试集中样本的5个重要变量的数据进行统计,结果见表2。
分析表2可知:与非事故样本相比,除最小会遇时间外,其他4个重要变量对船舶交通事故的发生影响较大,表现为无论是在训练集还是在测试集中,事故样本的这4个变量的均值和标准差均比非事故样本的小。而对于最小会遇时间变量,除了在训练集中事故样本的均值比非事故样本的大以外,在训练集中事故样本的标准差比非事故样本的小,在测试集中事故样本的均值和标准差均比非事故样本的小,说明最小会遇时间也对船舶交通事故的发生影响较大。统计结果从侧面验证了RF模型的科学性。
3.3 模型验证
3.3.1 模型对比
采用训练集中5个重要变量的有关数据训练SVM模型,再将测试集中的相关数据输入被训练后的SVM模型中,統计输出结果。
为验证经过变量筛选后SVM模型的效果,将变量筛选前后SVM模型的分类结果进行比较,见表3。
由表3可知,在数据相同的条件下,经RF筛选变量后所构建的SVM模型的分类效果更优,表现为:分类正确率Aca有所提高,达到88.64%,比筛选前的84.52%提高4.12个百分点;漏报率Rfn和误报率Rfp基本差不多。通过比较可以得出结论,经RF筛选变量后所构建的SVM模型不仅计算相对简单(变量由原来的13个减少到5个,所需处理的数据大幅减少),而且预测效果更优。
3.3.2 模型的可转移性测试
可转移性是验证模型是否具有普遍适用性的重要方法[16]。本文利用经过尹公洲水道交通事故数据验证过的两个SVM模型对福姜沙水道进行普遍适用性测试并比较。尹公洲水道和福姜沙水道均为长江下游内河水道,性质相似,具备可转移性测试的基本条件。福姜沙水道2010年4月至2020年3月共发生事故86起。采集这86个事故样本数据和该时间段内的793个非事故样本数据,对变量筛选前后的SVM模型的可转移性进行测试,结果见表4。
由表4可知,变量筛选后的SVM模型的可转移性测试结果比变量筛选前的好,表现为:变量筛选后的SVM模型的分类正确率Aca比变量筛选前的高,变量筛选后的SVM模型的漏报率Rfn和误报率Rfp均比变量筛选前的低。
综合比较表3与表4,可知:变量筛选前后的SVM模型对福姜沙水道的分类正确率虽然比对尹公洲水道的低,但仍超过80%,处于较高水平;不管是对尹公洲水道还是对福姜沙水道,变量筛选后的SVM模型分类正确率均比变量筛选前的高;变量筛选前后的SVM模型对尹公洲水道与福姜沙水道的漏报率差不多,均为9%左右;变量筛选后的SVM模型对福姜沙水道的误报率为10.12%,较对尹公洲水道的误报率12.52%低了2.40个百分点。因此,变量筛选后的SVM模型在预测特定水域交通风险方面效果较优,而且具有较好的普遍适用性。
4 结束语
运用随机森林模型对影响长江水道船舶航行安全的因素进行重要度排序,选出5个重要变量构建了新的支持向量机模型,基于历史事故数据对新模型进行验证,结果表明新模型预测效果更优。对验证后的模型进行可转移性测试分析表明,所建新模型具有较好的普遍适用性。需要说明的是,本文模型是基于长江下游水道实际情况建立的,验证数据也来自长江下游历史数据,该模型是否适用于其他航行水道还需要进一步验证。
参考文献:
[1]徐东星, 尹勇, 张秀凤, 等. 长江干线水上交通事故的灰色分析与预测[J]. 中国航海, 2019, 42(2): 59-65.
[2]张笛, 粱峥, 范存龙, 等. 基于贝叶斯网络的船舶自沉事故后果预测[J]. 中国航海, 2018, 41(1): 53-59.
[3]范中洲, 赵羿, 周宁, 等. 基于灰色BP神经网络组合模型的水上交通事故数预测[J]. 安全与环境学报, 2020, 20(3): 857-861. DOI: 10.13637/j.issn.1009-6094.2019.0597.
[4]王当利, 吕雪, 王雪佳, 等. 基于IOWA算子的水上交通事故组合预测模型[J]. 上海海事大学学报, 2018, 39(3): 34-40. DOI: 10.13340/j.jsmu.2018.03.006.
[5]徐东星, 尹勇, 张秀凤, 等. 基于改进三参数灰色模型的海上交通事故预测[J]. 中国航海, 2020, 43(1): 12-17.
[6]张逸飞, 付玉慧. 基于ARIMA-BP神经网络的船舶交通事故预测[J]. 上海海事大学学报, 2020, 41(3): 47-52. DOI: 10.13340/j.jsmu.2020.03.009.
[7]AHMED M M, ABDEL-ATY M A. The viability of using automatic vehicle identification data for real-time crash prediction[J]. IEEE Transportation on Intelligent Transportation System, 2012, 13(2): 459-465. DOI: 10.1109/TITS.2011.2171052.
[8]方诚, 胡甚平, 方泉根. 港口船舶引航风险预测[J]. 中国航海, 2008, 31(4): 388-391.
[9]PEREZ M A, SUDWEEKS J D, SEARS E, et al. Performance of basic kinematic thresholds in the identification of crash and near-crash events within naturalistic driving data[J]. Accident Analysis & Prevention, 2017, 103: 10-19. DOI: 10.1016/j.aap.2017.03.005.
[10]游锦明, 方守恩, 张兰芳, 等. 高速公路实时事故风险研判模型及可移植性[J]. 同济大学学报(自然科学版), 2019, 47(3): 346-352. DOI: 10.11908/j.issn.0253-374x.2019.03.007.
[11]卢艳民. 港口巷道水域交通安全风险评价研究[D]. 大连: 大连海事大学, 2019.
[12]王国波, 陈风云. 长江水上交通安全风险因素分析[J]. 港口科技, 2018(11): 38-42.
[13]ZOU Y J, HUA X D, ZHANG Y R, et al. Hybrid short-term freeway speed prediction methods based on periodic analysis[J]. Canadian Journal of Civil Engineering, 2015, 42(8): 570. DOI: 10.1139/cjce-2014-0447.
[14]苗旭, 王忠宇, 鄒亚杰, 等. 改进的固定交通检测器缺失数据综合修复方法[J]. 同济大学学报(自然科学版), 2019, 47(10): 1477-1484. DOI: 10.11908/j.issn.0253-374x.2019.10.013.
[15]CHAN K Y, DILLON T S, CHANG E. An intelligent particle swarm optimization for short-term traffic flow forecasting using on-road sensor system[J]. IEEE Transaction on Industrial Electronics, 2013, 60(10): 4714-4725. DOI: 10.1109/TIE.2012.2213556.
[16]SUN Jie, SUN Jian. Real-time crash prediction on urban expressways identification of key variables and a hybrid support vector machine model[J]. IET Intelligent Transport System, 2016, 10(5): 331-337. DOI: 10.1049/iet-its.2014.0288.
(编辑 贾裙平)
收稿日期: 2021-05-19
修回日期: 2021-09-27
基金项目: 江苏省教育厅基金(2017JSJG010);江苏高校“青蓝工程”(2019)
作者简介:
丁振国(1979—),男,黑龙江伊春人,副教授,硕士,研究方向为水上交通安全,(E-mail)jmidzg@126.com;
张树奎(1973—),男,安徽阜阳人,教授,博士,研究方向为港口、海岸与近海工程,(E-mail)zhangshkfy@163.com;
胡甚平(1974—),男,湖北通城人,教授,博士,研究方向为载运工具运用工程与安全工程,(E-mail)sphu@shmtu.edu.cn
