三角形边等差的解法及命题意图探究
2022-04-01刘小树
刘小树
(安徽省固镇县第一中学 233700)
1 试题呈现

2 试题解析
解法1(基本不等式法)
①

②
又由余弦定理及不等式,得
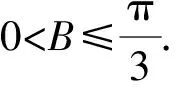

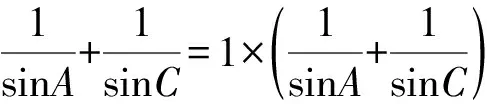
解法2 (配角三角公式变换法)
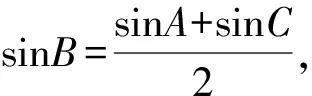
2sinB=sinA+sinC.




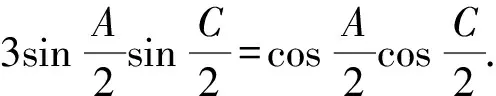

③
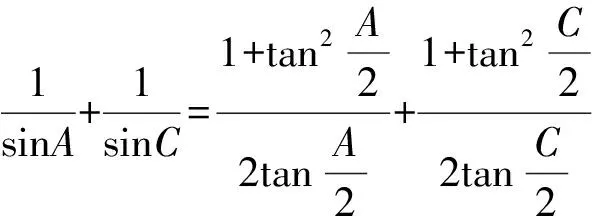

解法3 (建系构造椭圆法)
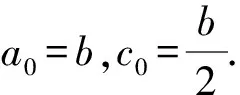
图1

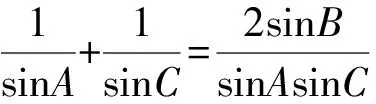
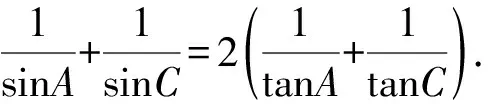
④
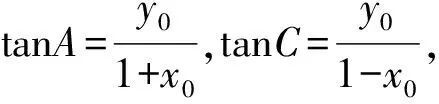
于是④化为
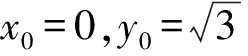
即当△ABC为等边三角形时取到最小值.
解法4(Jensen不等式法)
因为f(x)=sinx,x∈(0,π),f″(x)=-sinx<0,所以f(x)为上凸函数.
又2sinB=sinA+sinC,
所以3sinB=sinA+sinB+sinC
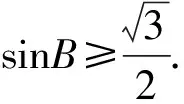
又因为2sinB=sinA+sinC,2b=a+c,
即a,b,c成等差数列.故b不是最大边.
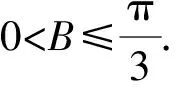
由基本不等式,得
sin2B≥sinA·sinC,当且仅当A=C取等号.
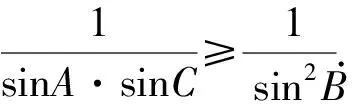



3 试题命题意图分析
试题用了4种方法解题,从解法1到解法4,解题要求难度逐渐加大,但是从考后调查发现,以上四种解法中,解法1,2仅少部分同学使用,解法3更是罕有人用,竞赛党同学容易想到解法4.试题难度系数0.22,区分度0.45,全市得分率为22.01%,最好的学校得分率也仅为40%,足见得分很低.大多数同学使用的方法让命题者欣慰又大跌眼镜:直接根据对称性取正三角形得到答案.这不得不让人思考,为什么会出现这种事与愿违的结果呢?可以从两个方面分析:一方面:大多数同学做16题常使用极限法、特殊图形或特殊值法,加上考试时间紧,压轴小题难度大,学生不敢在这里耗费时间,不得不取特殊图形法,而且验算后发现符合要求,就铤而走险解题.另一方面如果答案被学生轻而易举猜到,说明命题没有体现隐形性,要从命题角度考虑了.本题条件容易让考生联想到特殊图象法.
如果设置为
⑤
或cosA+2cosB+cosC=2,
⑥
或5cosA+5cosC-4cosAcosC=4.
⑦
相对来讲更能达到压轴和考查的目标.这是因为以上三种情形不易被考生猜到特殊图形,即使猜也没有理由.实际上这三种情形是等价的,最终都可以化为2b=a+c,这样既能达到考查要求,又不会被学生钻了空子,从而导致命题的尴尬境地.对于以上重新设置的条件为什么可以达到压轴目的呢,下面将转化过程具体证明,大家就一目了然了.
三种形式等价证明如下:

⟺a(1+cosC)+c(1+cosA)=3b
⟺a+c+acosC+ccosA=a+c+b=3b
⟺2b=a+c;
⑥cosA+2cosB+cosC=2
⟺cosA+cosC=2-2cosB
⟺2sinB=sinA+sinC
⟺2b=a+c;
⑦5cosA+5cosC-4cosAcosC=4

同⑥可化为2b=a+c或b=2(a+c)(舍).
不难发现, ⑤⑥⑦考查知识方法更全面、丰富、多元性、隐形性,可以多层次考查学生.另外大家还发现①至⑦都是等价命题.
高中数学命题原则一般是条件间要满足相容性,不得与公理定理概念相矛盾;力求语言描述准确无歧义;解题方法多元性,多种知识、思想相互沟通,对考生有启发性;试题素材要新颖、丰富、典型、隐形性,防止猜题.
命题是一项重要的工作,教师命题必须紧扣教学大纲和高考核心素养要求,合理命题,既要考查学生对基础知识,思想方法的掌握情况,又要让学生从问题中训练思维,提升能力,得到启发,使学生在解题中领悟命题意图,达到融会贯通,举一反三.命题要反复斟酌,力求做到没有失误,才能命出解法自然,形式完美的经典试题.
