平面向量数量积几何意义的应用

陈喜杨

(福建省莆田第六中学 351111)

高考中对平面向量数量积最值题目的考查常用其几何意义，这种题型涉及的条件通常是一个向量已知、另一个向量运动变化，考查学生的直观想象、逻辑推理、数学运算等核心素养，以及学生运用运动变化的思想分析问题、解决问题的能力.向量具有代数和几何的双重身份，不但有数的特征，而且有形的特点，是把代数与几何很好地连接起来的纽带，是数形结合的天然桥梁，向量中的很多问题常常借助于图形的几何性质，可以给抽象的运算以直观的解释，显得简捷方便.通过向量数量积解决问题使学生深入理解数学各知识之间的渗透，体会数学知识的抽象性、概括性和应用性，从而提高学生解题的正确率.

1 从几何角度理解平面向量数量积的定义

平面向量数量积的公式：a·b=|a|·|b|cosθ，其中θ=，|b|cosθ叫做向量b在向量a方向上的投影，因此投影是一个数量，不是向量.当θ=0°时投影为|b|，当θ为锐角时投影为正，当θ=90°时投影为0，当θ为钝角时投影为负，当θ=180°时投影为-|b|.故平面向量数量积a·b的几何意义是：向量a的长度|a|与向量b在向量a方向上的投影|b|cosθ的乘积.

平面向量数量积是向量的核心内容，属高考常考内容.利用平面向量数量积可以解决长度问题、夹角问题、垂直问题以及平行问题等.

2 平面向量数量积的应用

2.1基底与数量积的综合应用

当长度已知、向量夹角已知时，首先考虑用向量的三角形法则和平行四边形法则，选择两个长度已知、夹角已知的向量为基底来表示要求的向量，再结合平面向量数量积的几何意义求解.

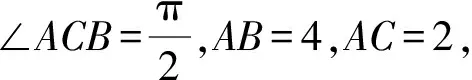
图1 图2

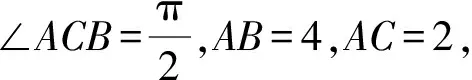
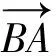
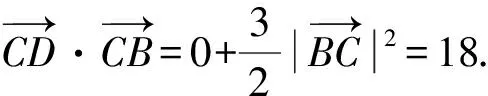
2.2 平面几何知识与数量积的几何意义的融合

几何与代数是高中数学课程的主要内容之一，在向量数量积几何意义的应用中，整合了数学中的代数运算和几何图形，引导学生通过数形结合，提升直观想象、数学运算及逻辑推理的核心素养.

图3

因为O为△ABC的外心,所以△ABC为直角三角形且∠BAC=90°.

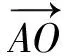
评注此题出现了三角形外心的条件，要能根据外心的条件直接联想到一些学过的平面几何的知识，并学以致用、联想推理从而达到解决问题的目的.题目中的已知条件反映了图形的几何性质,通过图形使得几何条件及各数量之间的关系得以直观地呈现出来.

2.3 平面向量的应用与转化思想

向量数量积常用的方法之一是转化，转化思想是指在解题时根据题目中的已知条件，结合定义、图象、性质或者公式把问题转化成我们能解决的数学问题，从而达到解题的目的.这个过程通常是把未知转化为已知、抽象转化为具体、复杂转化为简单，使我们能够用已学过的知识来解决遇到的问题.

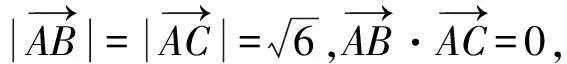
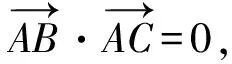
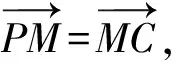
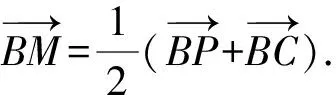
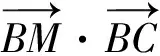
图4

此题使用了数量积的几何意义，应用转化思想把抽象的数学问题通过直观想象作出图象，使问题具体化、可视化，考查学生在处理数学问题时的迁移和应用.对比两种解法，由于本题是填空题，小题小做，故将数量积的几何意义联系数形结合进行求解，计算量较小，用到的知识点较少，更方便得出结果，而且也更容易判断出取最大值时点P的位置.

2.4 数量积几何意义在求数量积取值范围的应用

解析分别过点F，C作FM⊥AB，CN⊥AB交直线AB于点M，N，则点F，C在直线AB上的投影分别为点M，N.

如图5，根据正六边形图形的性质，得∠FAB=∠CBA=120°,故AM=BN=1.

图5

向量是高中很多知识点之间的一个连接点，是联系各个知识点的桥梁，是高中数学中重要的内容之一，发挥着举足轻重的作用.复杂背景下求向量数量积的最大值、最小值,关键是挖掘隐含条件来达到已知与未知的转化，化数为形，从而解决问题.