例析圆锥曲线解答题中的双向量系数问题

李 宁

(海南省海南中学 571158)

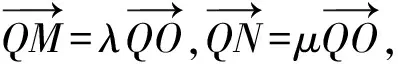
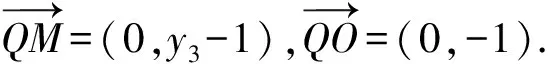
于是y3-1=-λ，即λ=1-y3.

同理，μ=1-y4.

由于P,A,M三点共线，有

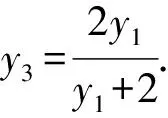
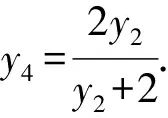
直线l斜率不为0，设其方程为x=m(y-1)，与y2=4x联立，得

y2-4my+4m=0.

从而y1+y2=4m，y1y2=4m.

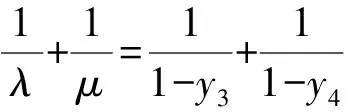
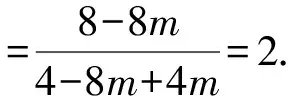
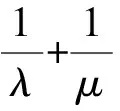
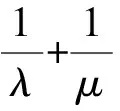
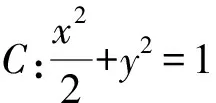
解析由题知F(1,0)，设A(x1,y1),B(x2,y2)，M(0,y0)，则

从而x1=λ(1-x1)，y1-y0=-λy1.

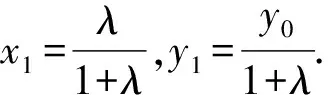
因为点A在椭圆C上，则

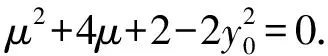
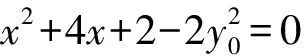
评注例2和例1类似，可以用相应点的横坐标或纵坐标来表示λ+μ，再利用韦达定理整体消元. 这里注意到例2的特殊性，A,B两点地位相同，利用点A在椭圆C上构建λ有关的二次方程，同理得到跟μ有关的二次方程，利用韦达定理直接得到λ+μ的值.

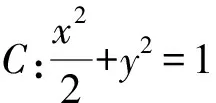
解析由题知F1(-1,0),F2(1,0)，设A(x1,y1),M(x2,y2),N(x3,y3)，则

故-1-x1=λ(x2+1)，-y1=λy2.

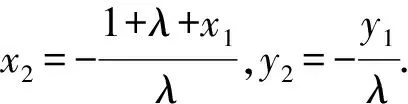
因为点M在椭圆C上，从而

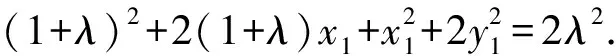
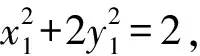
2(1+λ)x1=λ2-2λ-3=(λ-3)(λ+1).

由于λ>0，从而2x1=λ-3.

即λ=2x1+3.

同理μ=-2x1+3.

故λ+μ=6为定值.

评注从构图上来看，点A确定了以后，整个图形就能确定下来. 通过设点法，充分利用点在椭圆上消去二次项，得到参数之间的关系. 其实，也可以通过焦半径的计算来实现转化.

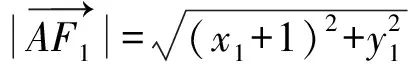
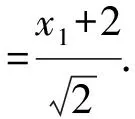
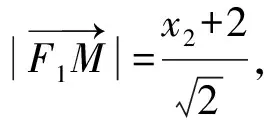
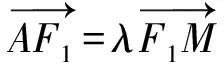
从而λ=2x1+3.

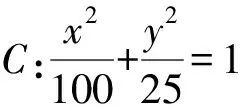
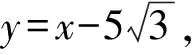
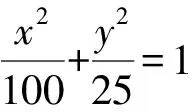
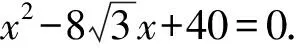
设A(x1,y1),B(x2,y2)，则

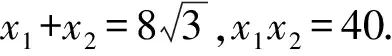
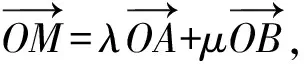
x0=λx1+μx2，y0=λy1+μy2.

由于M在椭圆上，从而

(λx1+μx2)2+4(λy1+μy2)2=100.

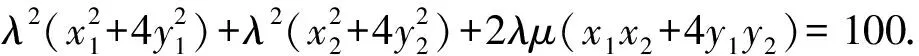
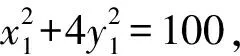
x1x2+4y1y2

=20,

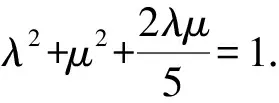
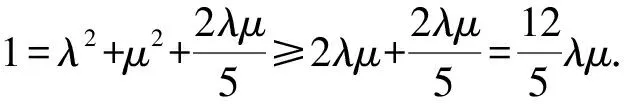
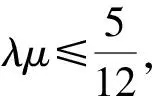
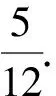
评注这里充分利用M,A,B三点在椭圆上来处理二次项，由直线方程和椭圆方程联立,通过韦达定理处理交叉项x1x2+4y1y2.

小结这类问题往往涉及到圆锥曲线上两个或更多动点，可以由题目给的向量条件沟通相应点的横坐标和纵坐标的关系，接下来就是消元. 可以分析整个图形的构图，考查是由动直线还是动点主导，从而考虑采取设线法还是设点法. 设线法，用韦达定理整体消元；设点法，利用点在圆锥曲线上来消元.

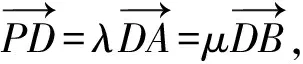
答案:λ+μ=-1.

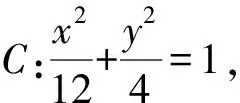
答案:(2,0).