例谈用换元法解题
2022-04-01刘大鹏
刘大鹏
(辽宁省黑山县第一高级中学 121400)
1 根式换元
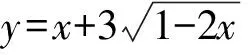
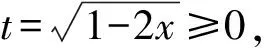

所以值域为(-∞,5].

2 增量换元
例2(自编题)设x≥0,y≥0,3x+y≤6,x+3y≤6,求u=2x+3y的最大值.
解析设t=6-(3x+y),s=6-(x+3y),
则t≥0,s≥0.
将x,y视为主元,解方程组得


评注用增量换元法解决线性规划问题新颖、简易,不需要繁琐的作图过程.
3 均值换元



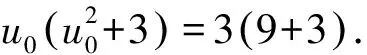

所以f(x0)=64,g(x0)=8,f(x0)g(x0)=512.
4 整体换元
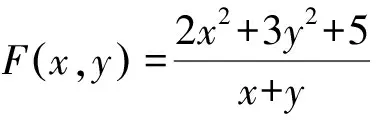
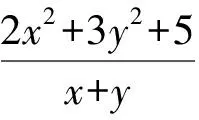
所以2x2-tx+3y2-ty+5=0.

5 倒数换元



x,y,z>0,xyz(x+y+z)≥1.
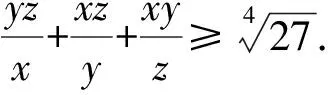


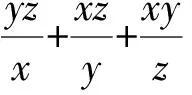
6 分母换元

证明令a+b=x,b+c=y,c+a=z,

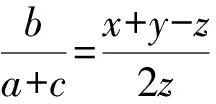



7 差量换元


不妨设0 令t=x2-x1>0, 所以x2=x1et,x1(et-1)=t. 令M(t)=e2t-2tet-1, 则M′(t)=2e2t-2et-2tet=2et[et-(t+1)]≥0. 所以M(t)>M(0)=0. 所以K′(t)>0. 解法1 令x=m+n,y=m-n, 代入已知,得3m2+13n2=5. (4S-5)k2-5Sk+4S-5=0. 当4S-5=0时,y=0或x=0; 当4S-5≠0时, Δ=25S2-4(4S-5)2=(13S-10)(10-3S)≥0, 比值换元还常用于解决极值点偏移问题. 令M(t)=t3-t2+t-1-(t2+t)lnt, 则M′(t)=3t2-2t+1-(2t+1)lnt-t-1 =3t(t-1)-(2t+1)lnt ≥3t(t-1)-(2t+1)(t-1) =(t-1)2>0, M(t)>M(1)=0, 所以K′(t)>0. 方法小结对条件式(x-a)2+(y-b)2=R2,可设x=a+Rcosθ,y=b+Rsinθ; 文[5]解答有误,本文加以修正. 所以tanθn+6=tan(θn+5π)=tanθn. 所以an+6=an,2009=6×334+5. 评注本例可用不动点法先求数列通项公式,再求a2009. 左=cos2α+cos2β+cos2γ =-sin2γ+sinγ+2


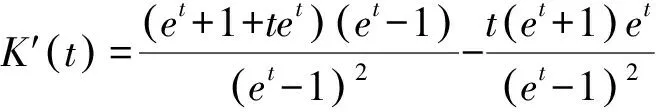
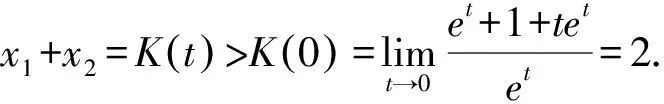
8 和差换元

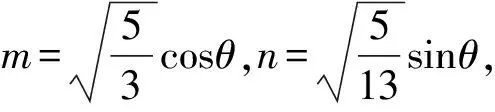
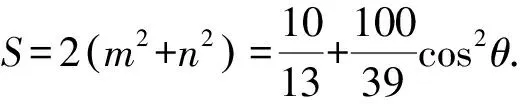

9 比值换元



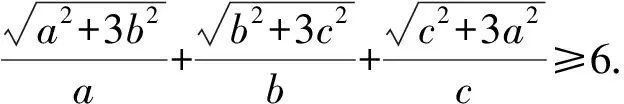


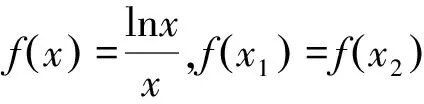


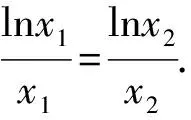


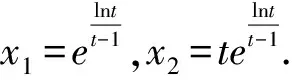



10 三角换元法