例谈多元最值问题的九种策略
2022-04-01白亚军
白亚军
(甘肃省永昌县第一高级中学 737200)
多元最值问题,指的是含有两个或两个以上变元的式子的最值求法问题,因为含有多个变元,所以学生害怕学习这一类问题,而这一类问题可以考查学生的综合能力,所以学生在平时的学习中,不要一味追求某一种解法,要学会从不同解法中汲取不同的思想方法,提高自身的数学核心素养.
1 利用不等式的性质


点评不等式的基本性质在高中数学中的应用是非常广泛的,一定要牢记不等式的基本性质.
2 利用绝对值不等式
例2求函数f(x)=|x2-a|在区间[-1,1]上的最大值M(a)的最小值.
解析注意到f(-1)=f(1),且2M(a)≥f(0)+f(1)=|a|+|1-a|≥|a+1-a|=1,

点评本题主要根据绝对值不等式|a|+|b|≥|a±b|求最值,根据不同情况选取.
3 利用均值不等式
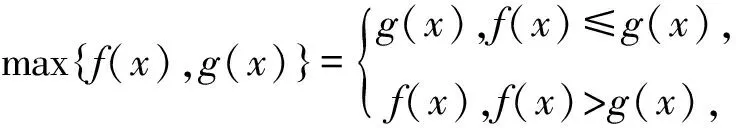
A.max{n(n),n(n+1)}>1
B.max{n(n),n(n+1)}<1
解析因为n(x)=x2+px+q的图象经过两点(α,0),(β,0),故n(x)=x2+px+q=(x-α)(x-β).
所以n(n)=(n-α)(n-β)=(α-n)(β-n),n(n+1)=(n+1-α)(n+1-β).

点评通过已知条件转化构造和为定值,再利用基本不等式使问题自然获解.
4 利用柯西不等式

解析设

点评柯西不等式往往不能直接使用,需要对数学式子的形式进行变化,拼凑出与一般形式的柯西不等式相似的结构,才能应用.
5 分类讨论





点评对于多元函数最值问题,有时需将题目条件中包含的全体对象分成若干类,再分类讨论.
6 待定系数法

点评当运用不等式性质较难达到目标时,有时可引入参数作为待定系数,再根据题意解决问题.
7 构造函数
例6 设a,b,c∈R,f(x)=x3+ax2+bx+c(-1≤x≤1),求min{max|f(x)|}.

设x=cosθ,θ∈[-π,π],则



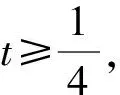
点评根据题设或所具有的特征构造出满足条件或结论的函数,借助于函数性质解决问题.
8 利用韦达定理
例7若a,b,c>0且a+b+c=12,ab+bc+ca=45,求min{max{a,b,c}}.

点评一定条件下求某些代数式的最大值、最小值,如果将其与一元二次方程中的根与系数关系及根的判别式联系起来,将会给我们提供一种十分巧妙的解题思路.
9 数形结合
例8设f(x)=min{2x,16-x,x2-8x+16}(x≥0),其中min{a,b,c}表示a,b,c三个数中的最小值,则f(x)的最大值为( ).
A.6 B.7 C.8 D.9

图1
解析画出y=2x,y=16-x,y=x2-8x+16的图象,观察图1可知,当x≤2时,f(x)=2x;当2
点评数形结合就是根据数学问题的条件和结论之间的内在联系,分析其代数意义,又揭示其几何直观,使数量关系的精确刻画与图形巧妙地结合.
通过以上多元最值问题的剖析,最基本的处理策略就是减元,研究一元函数的思想方法是研究多元函数的基础,在任何情况下,学生都要扎实抓好基础知识、基本技能、基本思想方法的落实,在教学中做到“点点”落实,否则“欲速则不达”.
