基于磁场变换器的双向加载式管件电磁翻边成形效果研究

邱立，田茜，吴伟业，王成林,3

基于磁场变换器的双向加载式管件电磁翻边成形效果研究

邱立1a,1b，田茜1a,2，吴伟业1a，王成林1a,3

（1. 三峡大学 a. 电气与新能源学院；b. 梯级水电站运行与控制湖北省重点实验室，湖北 宜昌 443002；2. 国网湖南省电力有限公司长沙供电分公司，长沙 410015；3. 国网重庆市电力公司物资分公司，重庆 401121）

针对传统管件电磁翻边时，仅采用径向电磁力加载，翻边效果不够理想的问题，提出基于磁场变换器的双向加载式管件电磁翻边技术。使用COMSOL软件构造二维轴对称分析模型，分析线圈参数的改变对径向、轴向电磁力和管件翻边效果的影响。在此基础上，进一步在电磁力、变形速率、管件变形轮廓3个方面将新型加载方式与传统管件电磁翻边技术进行对比。在传统管件电磁翻边中，管件翻边角度只能达到45°，而径、轴向电磁力的双向加载方式使最大翻边角度增加至90°。这一新型加载方式能够实现预期效果，促进管件电磁翻边在工业领域的发展。

管件电磁翻边；磁场变换器；双向加载；翻边角度；驱动线圈

电磁翻边是铝合金材料翻边的有效方法之一，与传统冲压翻边相比，它的优点有成形速度快、成形极限高、回弹小等[1-3]。许多学者针对管件电磁翻边进行了一定研究。Li等[4]提出了利用分段线圈产生的梯度电磁力来满足异形变径管变形力场要求的新型梯度电磁成形方法，由于线圈的尺寸和形状受管结构的限制，当管的尺寸较小时，该方法存在缺陷。Xiong等[5]提出了一种利用电磁吸力进行管材胀形的新方法，这种方法在一定程度上可以成形尺寸较小的管件。但是在管件电磁翻边成形的实际应用中，较小的管件还是会因为碰撞到线圈内层而导致成形结果不佳。虽然通过扩大线圈的内径可以避免碰撞，但这种措施因为管件和线圈间距离的增加，也会导致作用的电磁力衰减。Xiong等[6]基于双线圈对小型管件进行了翻边成形研究，这一方法可为小尺寸管材电磁翻边的验证提供极大的便利，但双线圈的工装较为复杂。张望等[7]提出通过双线圈加载径、轴双向电磁力对管件进行翻边，翻边角度较传统单线圈加载显著提高，但仍然存在双线圈工装复杂的问题。

除了采用驱动线圈直接加载的方式，也可以利用磁场变换器驱动工件变形。磁场变换器是电磁成形中常用的辅助配件，通过改变磁场变换器形状加强某处磁场分布，极大提高了线圈寿命。李春峰等[8]通过实验研究了工件在不同材料、不同内外径比的磁场变换器作用下的胀形效果，对磁场变换器材料的选择及确定磁场变换器的最佳内外径比等方面进行了研究和分析。Yu等[9]利用ANSYS有限元软件，模拟并分析了在电磁缩颈时，螺线管磁场变换器的有效面积、直径等对其工作状态的影响，发现磁场变换器能产生更大的径向电磁力。三峡大学Qiu等[10]采用磁场变换器加载管件胀形，磁场变换器会将电磁力集中在管件端部，从而在管件上产生凹形电磁力分布，使管件变形均匀。

通过上述分析，发现之前的研究学者们改变电磁力分布的措施大多是改变线圈结构等参数，但这样会带来线圈工装复杂、成本高等问题，不适用于工业化生产。目前通过引入磁场变换器改善电磁力分布，增强某一特定区域的电磁力这方面的研究较少。

文中提出基于磁场变换器的管件电磁翻边，以增强轴向电磁力，实现径、轴向电磁力的双向加载。首先建立引入磁场变换器的管件电磁翻边仿真模型，研究线圈结构参数对径向与轴向电磁力分布和翻边效果的影响，再将其与传统单线圈管件翻边在电磁力大小、翻边速率和变形轮廓等方面进行对比。仿真结果显示，采用磁场变换器实现的双向电磁力加载模型，管件电磁翻边角度提升1倍，能够达到90°。

1 基本原理

磁场变换器是电磁成形的基础辅助工具，利用趋肤效应和具有狭缝的结构相互配合，改变线圈产生的磁场位形，在磁场变换器内外壁产生密度不同的感应电流，从而使电流密度大的外壁产生更集中的磁场，故增强了某一特定区域的电磁力，结构如图1所示。

图1 磁场变换器结构[11]

在文献[11]中，通过对磁场变换器的二维轴对称建模和三维建模进行对比，验证了二维轴对称磁场变换器模型的有效性和准确性。图2为管件电磁成形磁场变换器的电流分布情况。充电后电容开始放电，驱动线圈内出现脉冲电流，此时磁场变换器内壁产生方向相反的感应涡流，由于狭缝存在而导致感应电流从内壁流向外壁，感应涡流从外壁再次通过狭缝流向内壁形成回路。磁场变换器内壁的高度远大于外壁，而内外壁总电流大小相等，所以其外壁电流密度远大于内壁电流密度。外壁的感应涡流产生的磁场与线圈中脉冲电流产生的磁场叠加，在管件中产生感应涡流[7,12]，从而在洛伦兹力的作用下实现管件电磁翻边。

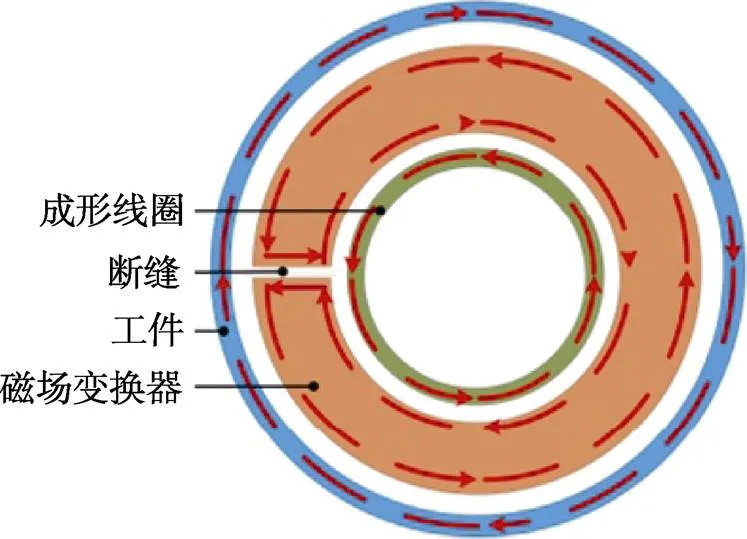
图2 磁场变换器电流分布[11]

洛伦兹力可以分解为轴向分量和径向分量，即轴向洛伦兹力（）和径向洛伦兹力（），表达式如下：

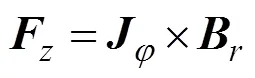
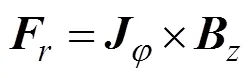
式中：为圆周方向的环形涡流；和分别为磁通密度的径向和轴向分量。

如图3a所示，在传统单线圈电磁翻边系统中，驱动线圈放电后，管件端部的轴向磁通密度小于管件中部，且磁通密度主要为轴向分量，故管件端部主要受径向电磁力，受到的轴向电磁力较小。这导致管件翻边在完成径向胀形后轴向的变形并不充分，翻边角度仍不够大。

为克服这一问题，文中在成形管件和驱动线圈之间引入新型磁场变换器，构建径向和轴向电磁力双向加载的管件电磁翻边模型，如图3b所示。其中，驱动线圈、成形管件、磁场变换器同轴放置，轴向紧密贴合，图3中点为管件端部中点。与已有变换器的集磁作用不同，文中磁场变换器的作用是改变磁场的方向，分析如下。

驱动线圈放电后，磁场变换器和管件中产生感应涡流，置于端部的驱动线圈产生的磁通以径向为主，故产生的电磁力以轴向电磁力为主。通过引入该磁场变换器，其内外壁形成的电流回路会产生轴向磁通，改变磁场在管件端部的方向，该轴向磁通与管件感应涡流相互作用，形成了较大的径向电磁力，与端部线圈产生的轴向电磁力共同作用，实现电磁力双向加载驱动管件翻边。磁场变换器的存在会使线圈作用于工件的能量产生损耗，增加线圈的层数、尺寸可以使工件达到更好的翻边角度。这样的加载方式，导致在翻边过程中管件受到双向加载的电磁力，磁场变换器为线圈提供的径向电磁力使管件发生胀形，端部线圈为管件提供轴向电磁力，进一步增大翻边角度[7]。

图3 电磁翻边几何结构

2 数值仿真

电磁成形中，电磁场、结构场和温度场具有强耦合关系，有限元分析可以用来精确模拟电磁成形过程。通过COMSOL构造传统单线圈管件翻边模型和含磁场变换器的管件翻边模型，具体模块如下。

1）全局常微分方程和微分代数方程模块，用于求解微分方程组和对外部电路进行仿真。当电路中存在新型磁场变换器时，若忽略线圈和管件之间的耦合，管件电磁成形的等效电路如图4所示。电路中放电电容为320 µF，线路电感0为12 µH，线路电阻0和续流电阻d分别为35 mΩ和260 mΩ，放电电压0为3.2 kV[13]。

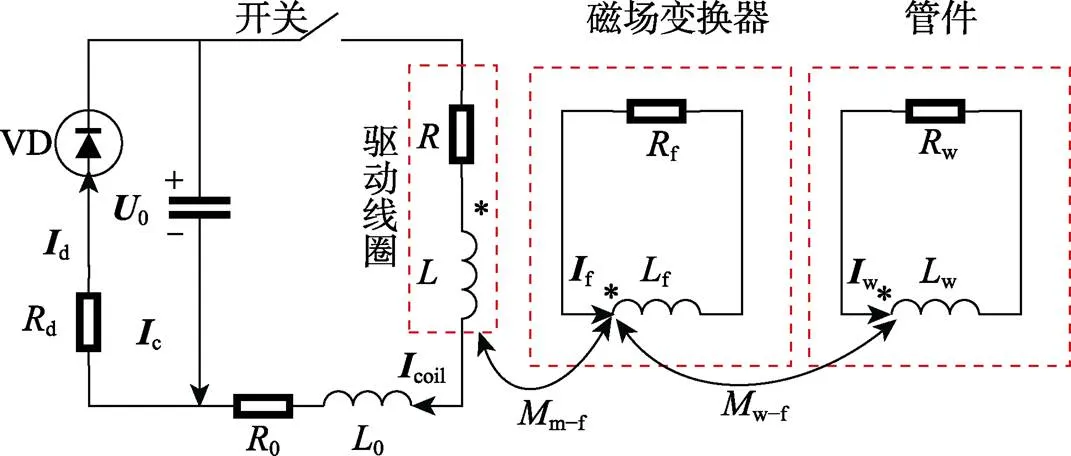
图4 基于磁场变换器的管件电磁成形等效电路

根据基尔霍夫定律，可以推导出以下方程：

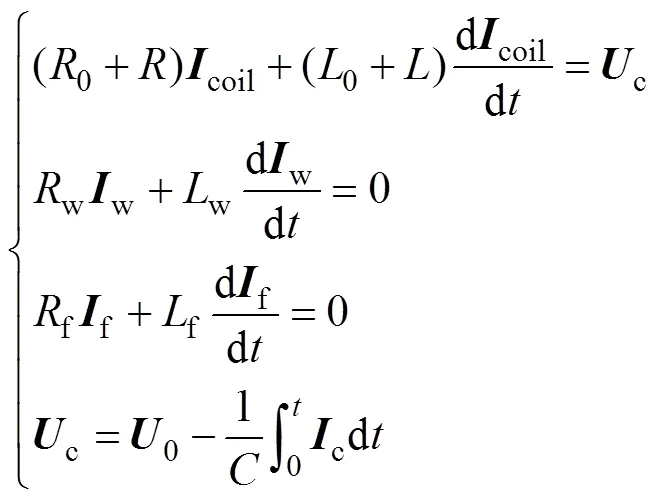
式中：c为电容器两端电压；c为驱动线圈电流；w为管件中的感应涡流；f为磁场变换器中感应涡流；为驱动线圈电阻；为驱动线圈电感。

2）磁场模块：用于获得磁场和电磁力分布，并将获得的电磁力传递给固体力学模块。管件内的感应涡流主要为环形分量，磁场的麦克斯韦方程为：

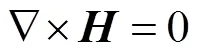
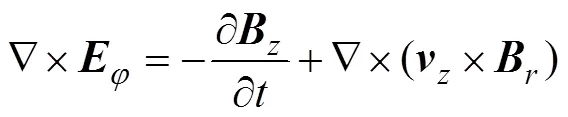
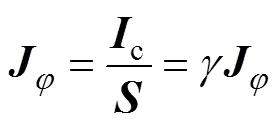
式中：为管件内的感应涡流密度；为电场强度；为磁通密度；为管件速度；为管件电导率；，和分别表示矢量的径向、环向和轴向[12-14]。

3）固体力学模块：分析管件受到电磁力后的变形行为，并将变形量传递给磁场模块，实现电磁-结构耦合。当管件受力时，它将遵循牛顿定律=，管件的力与位移之间的关系见式（9），其中为管件应力张量，为电磁力体积密度矢量，为管件密度，为管件位移矢量。

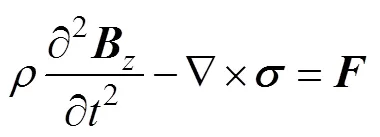
本模型模拟AA6061-O管材，其准静态应力-应变曲线的拟合曲线及相应计算拟合曲线如图5所示，该管材本构方程为[15]：

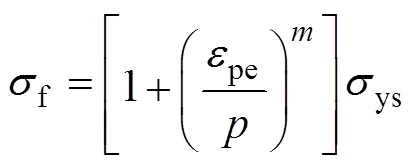
式中：ys为管件的初始屈服应力；f为管件高速变形时的流动应力；为应变率硬化参数；为粘性参数，在多数电磁成形数值分析中通常取=6500，=0.25。

上述仿真模型通过引入磁场变换器，增大了径向电磁力，从而实现了径、轴向电磁力双向加载。由单线圈加载下的管件电磁翻边实验[15]可知，增加线圈匝数可以增强轴向力进而弥补管件翻边过程中因径向力不足导致的翻边不充分，进而增大管件翻边角度，实验结果见图6。下面将在数值仿真及该实验结果的基础上，进一步分析线圈的内外径参数对径向、轴向电磁力和管件翻边效果的影响，并与传统管件电磁翻边技术进行对比。

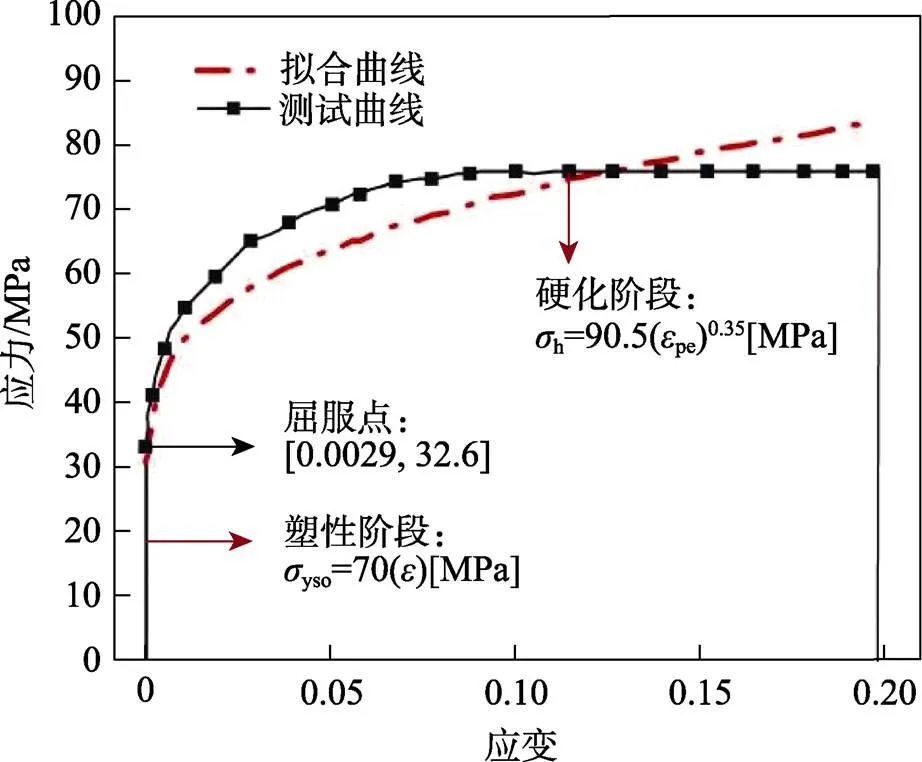
图5 AA6061-O管材的准静态应力-应变曲线的拟合曲线及相应计算拟合曲线[7]

图6 不同放电电压下4匝线圈与6匝线圈的翻边效果[15]

3 改变线圈参数对管件翻边效果的影响

管件材料为铝合金AA6061-O，其厚度为2 mm、长度为65 mm、外直径为79 mm。驱动线圈采用横截面积为2 mm×4 mm的铜导线多层多匝紧密绕制而成，骨架为环氧树脂，匝间使用高强度Zylon纤维加固。

由于管件自身参数不易改变，本章在基于磁场变换器的管件翻边模型中（如图3b所示），通过改变线圈参数，分析径向和轴向力双向加载对管件翻边效果的影响。下面将采用保持线圈长度不变，固定外半径、改变内半径和固定内半径、改变外半径这2种方法来改变线圈层数，从而研究改变线圈参数对管件所受径向力、轴向力以及翻边效果的影响。

3.1 改变线圈内半径

外电路参数不变，放电电压设定为3.2 kV，固定线圈外半径为36.4 mm。取6组内半径大小不同的线圈进行管件电磁翻边，管件的内半径分别设置为12.4，14.6，16.8，19，21.2，23.4 mm，观察并测量管件的成形轮廓，对仿真中得到的径、轴向电磁力进行分析，对比得到改变线圈内半径对管件翻边效果的影响。

3.1.1 径向、轴向力的变化

图7为在6组不同内半径下，管件上的径向与轴向电磁力随时间的变化情况。由图7a可知，在不同参数的线圈加载下，管件所受径向电磁力随着时间先增大，达到峰值后开始衰减。其中，线圈内半径越大，到达峰值的时刻越早，径向电磁力的峰值越小。图7b中径、轴向力的变化规律与图7a相同。可以看出，改变线圈内半径并不会改变径、轴向力的分布趋势。保持线圈外半径不变，当内半径增大时，管件所受径、轴向力均减小。

3.1.2 变形轮廓

图8为在不同内半径下，管件进行电磁翻边的成形轮廓。当线圈的内半径逐渐增大时，翻边角度逐渐减小，管件的成形轮廓也随之发生显著变化。当内半径为最小值12.4 mm时，管件翻边角度大于90°，当内半径为最大值23.4 mm时，管件翻边角度远小于90°，翻边角度越大则表明管件的翻边效果越好。

分析可知，保持线圈外半径不变，当内半径增大时，由于线圈层数减小，管件所受径、轴向力以及翻边角度均减小。

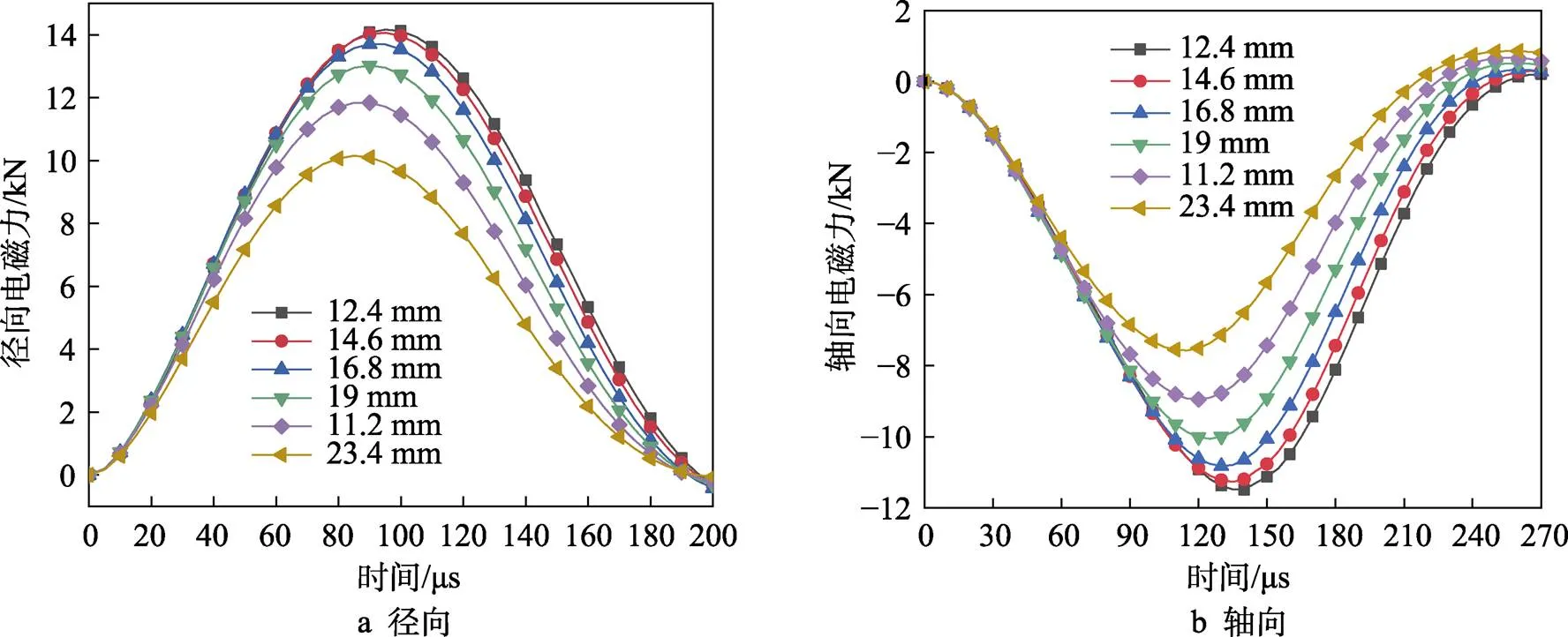
图7 改变线圈内半径的电磁力变化

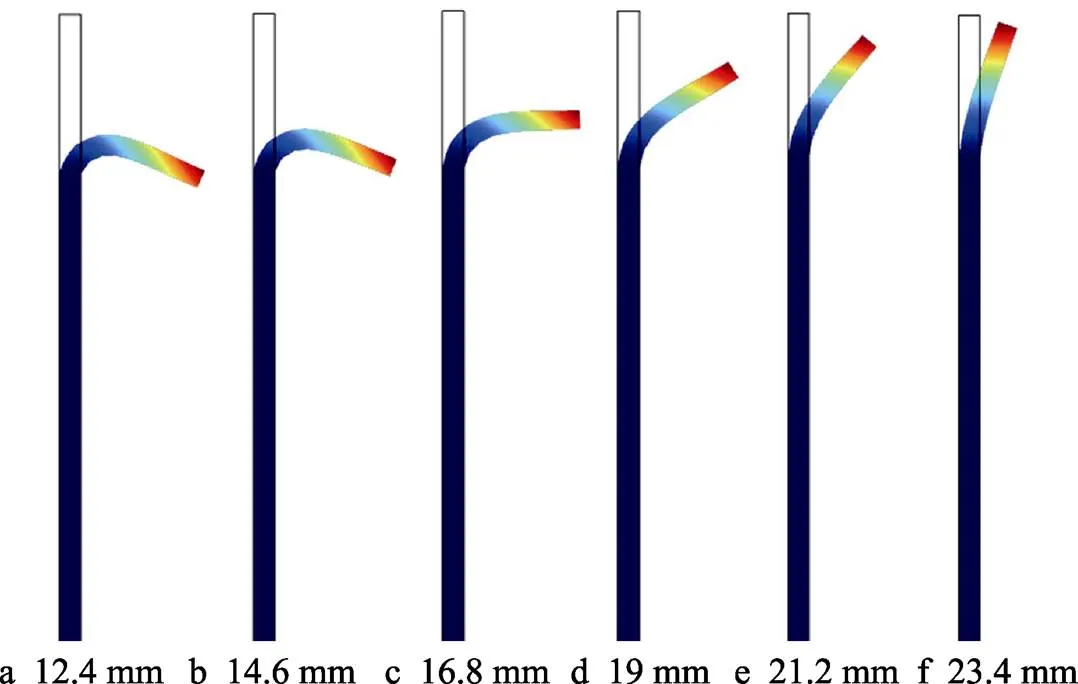
图8 改变线圈内半径的成形效果

3.2 改变线圈外半径

上节探讨了改变线圈内半径对管件翻边效果的影响。本节固定线圈内半径为16.8 mm，调整管件的外半径分为32，34.2，36.4，38.6，40.8 mm，其余参数同上节保持不变。

3.2.1 径向、轴向力的变化

图9为管件所受径、轴向电磁力随时间的变化情况。可以看出，在不同外半径的线圈加载下，径、轴向力的分布趋势并未改变。由图9a可知，管件所受径向电磁力随着时间先增大，到达峰值后开始衰减。其中，随着线圈外半径的增大，径向电磁力的峰值先增大再略微减小。由图9b可知，管件所受轴向电磁力随着时间的变化趋势与径向力相同。其中，随着线圈外半径增大，轴向电磁力的峰值逐渐增大。

3.2.2 变形轮廓

图10为在不同外半径下，管件进行电磁翻边的成形轮廓。如图10所示，当外半径为最小值32 mm时，管件翻边角度远小于90°，当外半径为最大值40.8 mm时，管件翻边角度大于90°。由此可知，保持线圈内半径不变，当外半径增大时，管件所受轴向力增大，径向电磁力和翻边角度均先增大，再略微减小。

通过上述仿真模拟和数据分析可知，管件翻边角度随着所受径向和轴向电磁力大小变化而变化，径、轴向力越大，管件翻边角度越大。因此与传统单一径向电磁力加载方式相比，径、轴电磁力双向加载下管件翻边更充分。

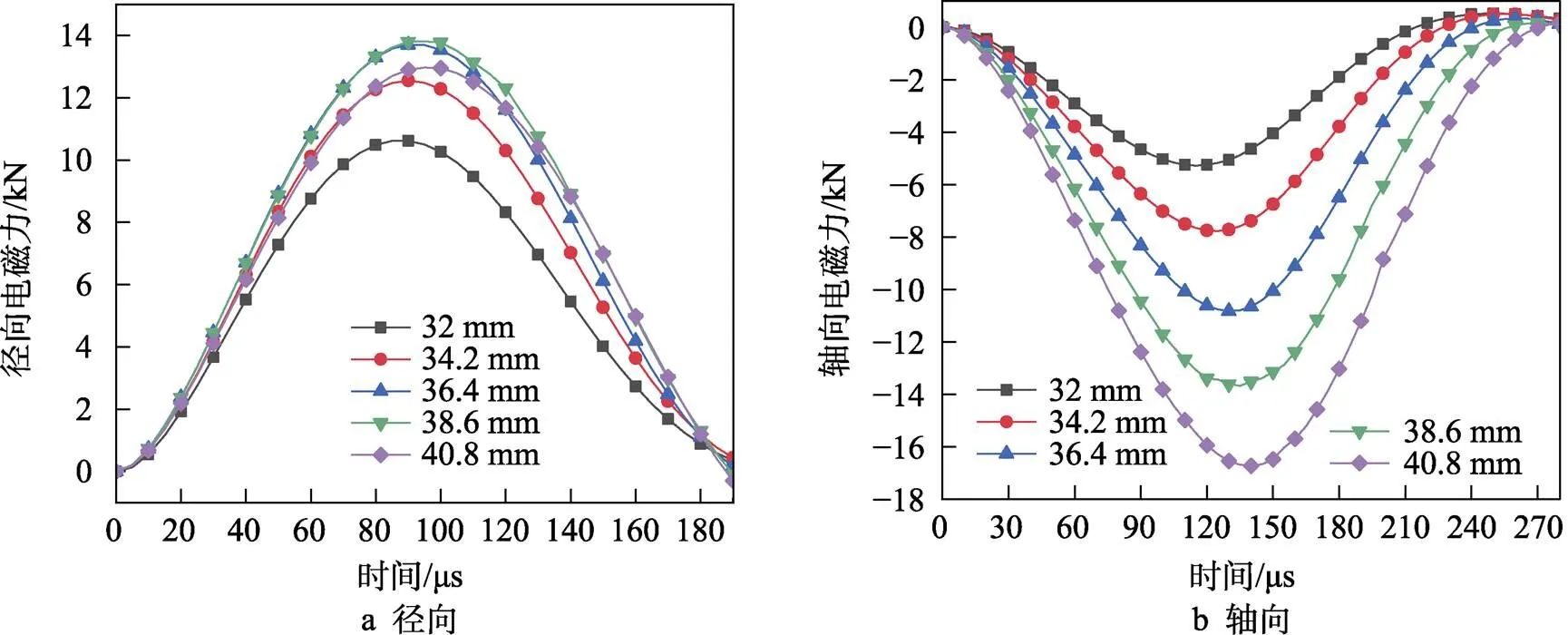
图9 改变线圈内半径的电磁力变化

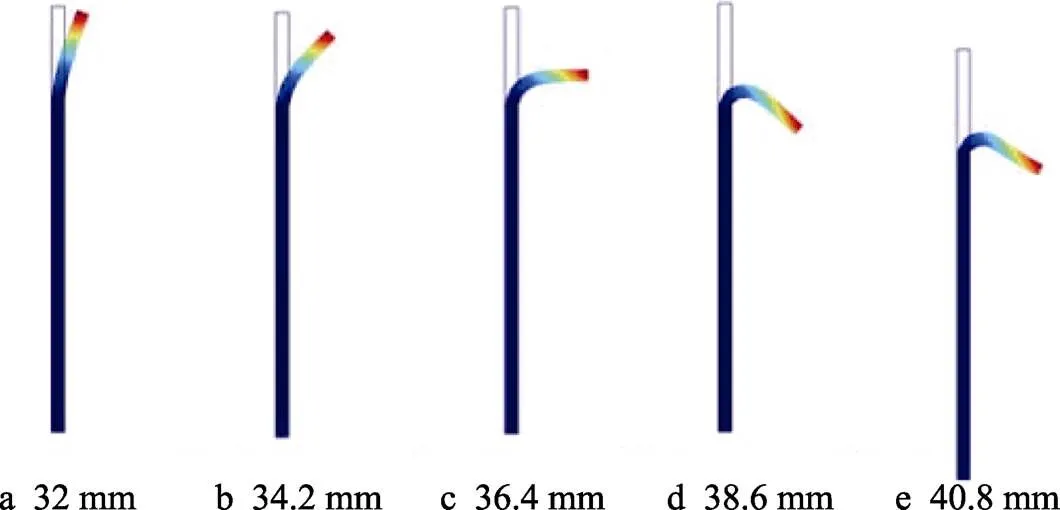
图10 改变线圈外半径的成形效果

4 管件翻边效果的对比分析

由于传统驱动线圈加载时，管件端部主要受到径向电磁力而导致翻边不充分。由上节分析可知，电磁力双向加载时管件翻边更加充分，故将线圈和磁场变换器同轴放置，由线圈提供较大的轴向电磁力，而磁场变换器改变了管件端部磁场方向，在管件端部产生径向电磁力。

本章通过讨论单一径向电磁力和径、轴向电磁力加载的不同，从管件所受电磁力、变形速率、变形轮廓3个方面，分析基于磁场变换器加载的模型与传统模型的管件翻边效果。传统驱动线圈、轴向线圈及管件的几何参数如表1所示。外电路参数不变，放电电压设定为3.2 kV。

4.1 电磁力

新型与传统2种翻边模式下管件所受径向电磁力和轴向位移的规律如图11所示，当计算时间>220 µs时径向力趋于0。图12为2种加载模式下管件所受轴向电磁力和管件轴向位移的规律对比，当计算时间>240 µs时径向力趋于0。

表1 传统驱动线圈、轴向线圈及管件的几何参数

Tab.1 Geometric parameters of traditional drive coil, axial coil and tube fittings

2种模式下放电电压和外电路参数相同，故总放电能量相等。由图12可知，在新型翻边模式中，端部线圈提供的轴向力较传统加载方式提高了2.63倍，由于放电能量相等，磁场变换器作用于管件的径向力略小于传统加载方式。这种加载模式下，管件的径向位移增大了0.38倍，而轴向位移增大了2倍。管件受到不小的径向力的同时，所受轴向力大大提高，这种双向电磁力加载模式，使径向位移有所提高、轴向位移显著提高，放电过程取得了更好的翻边效果。

4.2 变形速率

图13a为管件上点处径向变形速率和径向位移随时间变化的规律。图13b为点轴向变形速率和轴向位移随时间变化的规律。可以看出，加载磁场变换器后，由于双向电磁力加载，管件径向和轴向的变形速率都显著提高，径向变形速率比传统模式提高了12.1 m/s，轴向变形速率提高了25.2 m/s。结合图12，由于端部驱动线圈的作用使管件受到的轴向电磁力提高了2.63倍，该双向电磁力加载模式提高了管件的轴向变形速率。电磁成形是一种高速率的成形方式，图13中，300 µs后的径向和轴向速度波动不会对翻边产生影响。

4.3 管件变形轮廓

图14和图15分别为传统单一径向电磁力加载和基于磁场变换器的径、轴向双向电磁力加载的管件翻边轮廓。由图14可知，传统模式下，管件主要在径向电磁力作用下发生胀形。在放电过程中，翻边角度随着时间逐渐增加，=500 µs时达到最大翻边角度，但远小于90°。由图15可知，加载磁场变换器后，管件不仅受到磁场变换器作用的径向电磁力，也受到顶端线圈作用的轴向电磁力。管件在双向电磁力作用下，虽然放电初始阶段翻边角度与图14相比没有明显提高，但=500 µs时翻边角度达到最大值90°。

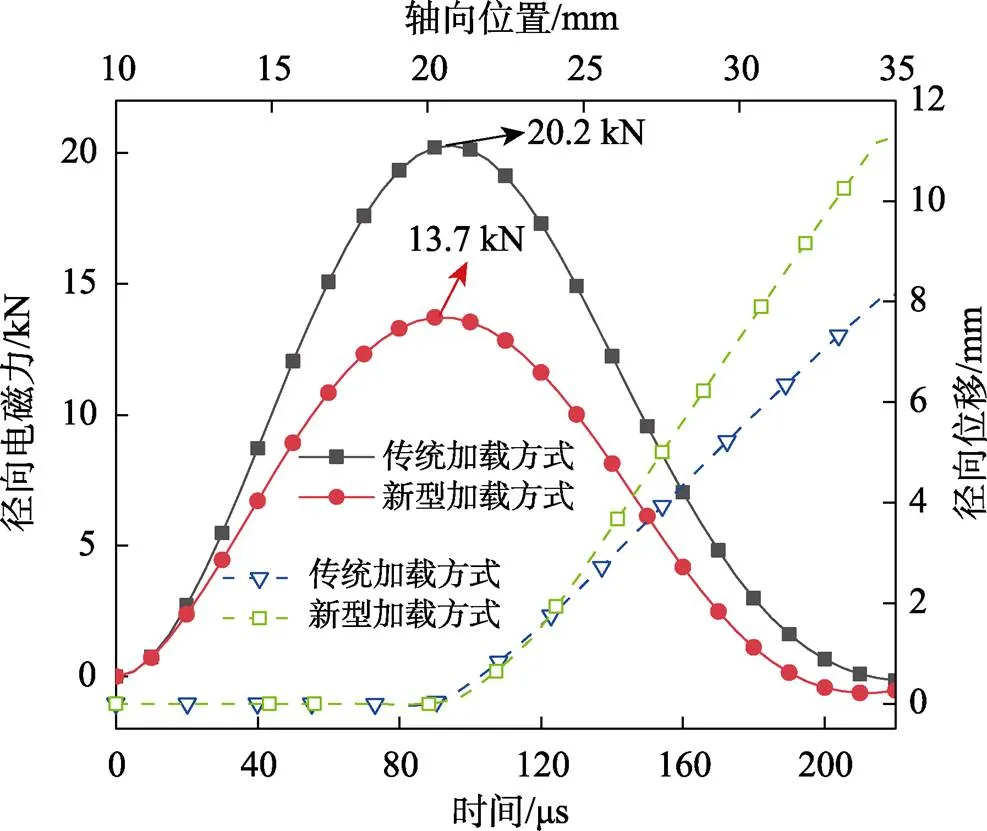
图11 径向电磁力与径向位移位置对比

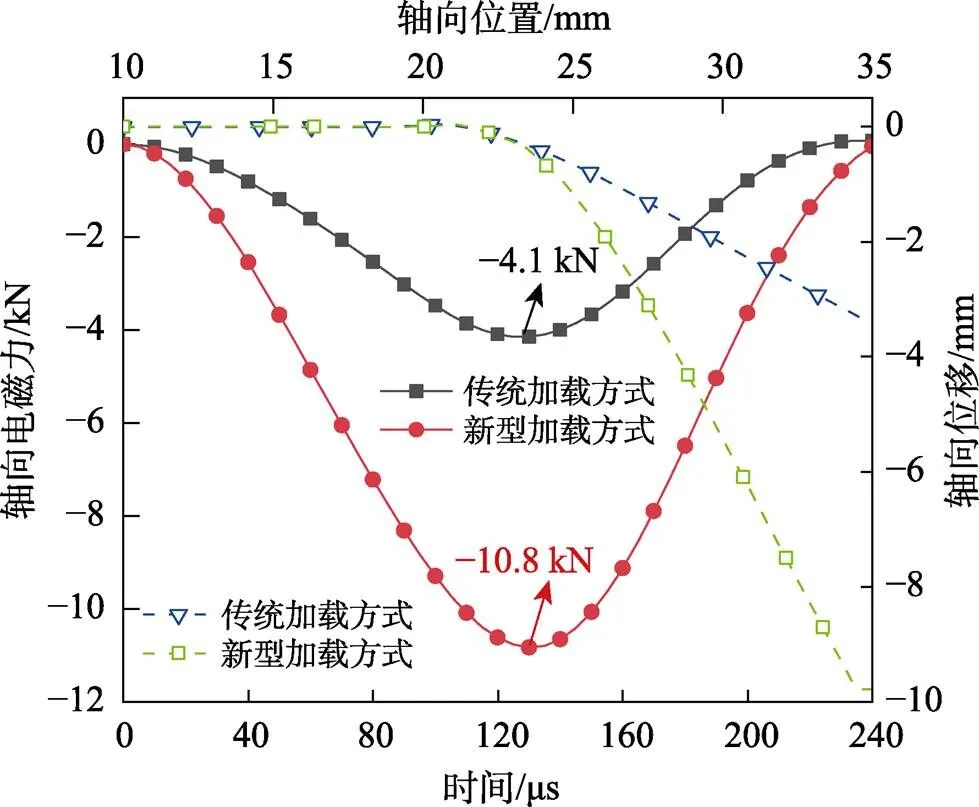
图12 轴向电磁力与轴向位移位置对比

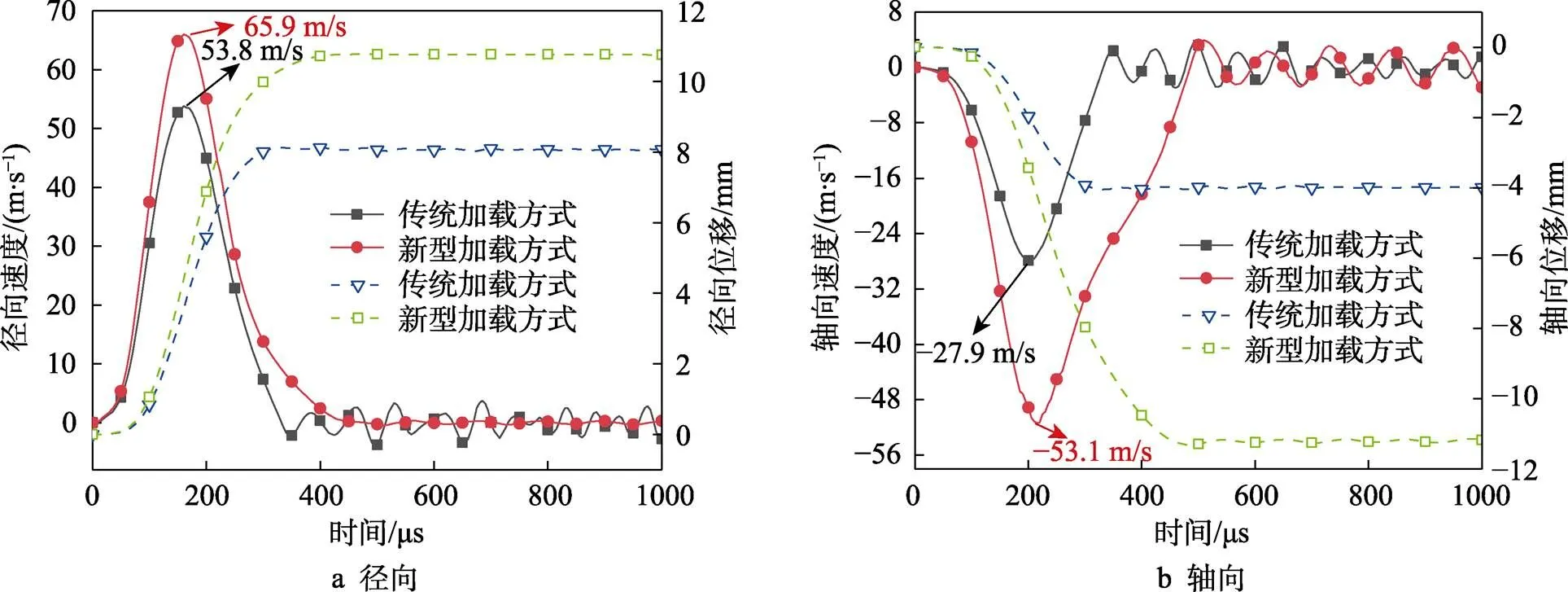
图13 速率与位移时间对比

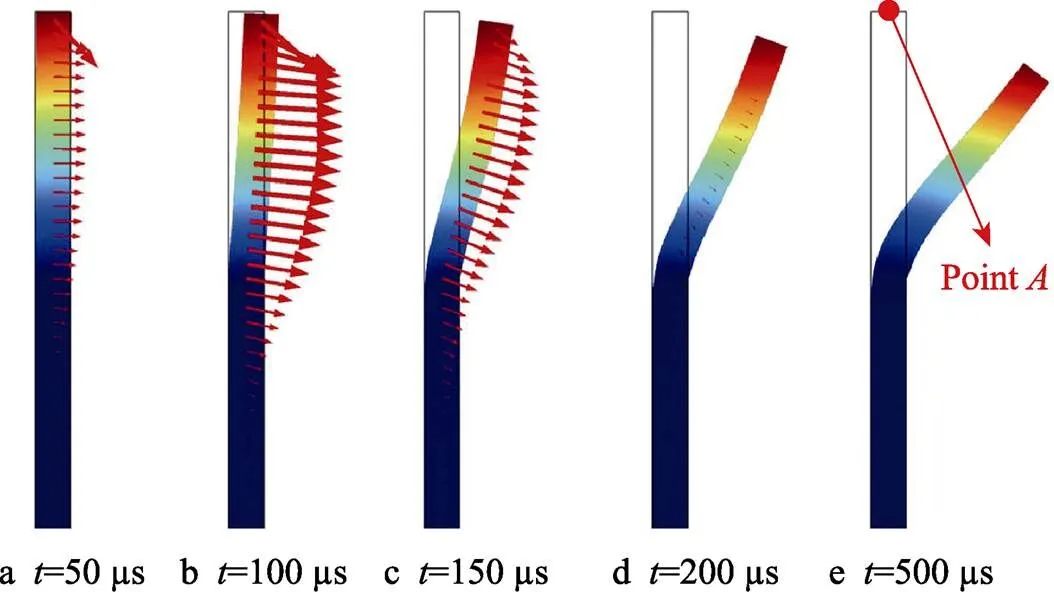
图14 传统管件翻边过程

图15 磁场变换器加载下的翻边过程

图16为在=500 µs时2种翻边模式的变形轮廓对比。其中图16a为传统管件翻边模型，在=500 µs时翻边角度为45°；图16b为在磁场变换器加载下的管件翻边模型，在=500 µs时翻边角度为90°。由此可见，在径、轴向力的双向加载下，管件翻边效果大大提高。

分析可知，当<500 µs时，由于翻边角度较小，管件内侧主要在径向力作用下发生变形，2种模式下管件所受径向力差异不大，所以翻边角度差异不大。当>500 µs时，翻边角度超过45°，管件会进一步受到轴向力作用发生变形。由于双向电磁力加载模式中的轴向力较传统模式显著提高，使管件的翻边极限大大提升，最大翻边角度由传统模式中的45°增加到90°。

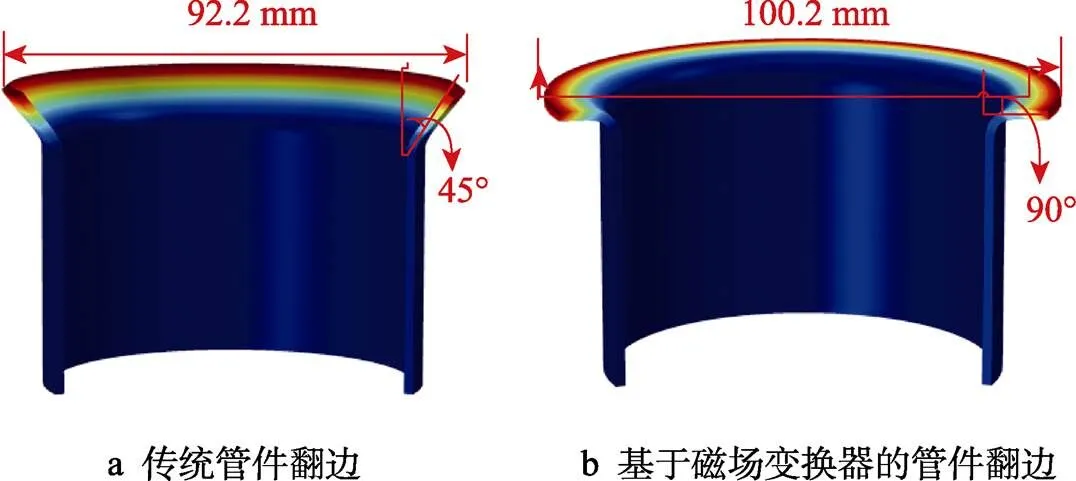
图16 2种翻边模式的翻边对比

5 结语

通过改变线圈内半径和外半径，发现管件翻边受径、轴向电磁力的双重影响。为解决传统线圈加载下轴向电磁力不足导致管件翻边角度较小的问题，提出了基于磁场变换器的加载模式，实现了电磁力的双向加载。对比传统线圈加载时和基于磁场变换器的线圈加载时管件翻边角度、所受径/轴向电磁力大小和变形速率，可知，新型翻边模式中管件所受轴向电磁力提高了2.63倍，使管件翻边角度达到90°，进一步给出线圈、磁场变换器的最佳参数。显然基于磁场变换器的双向电磁力加载模型，在一定程度上解决了管件翻边角度问题。

[1] QIU Li, YU Yi-jie, XIONG Qi, et al. Analysis of Electromagnetic Force and Deformation Behavior in Electromagnetic Tube Expansion with Concave Coil Based on Finite Element Method[J]. IEEE Transactions on Applied Superconductivity, 2018, 28(3): 1-5.

[2] BALANETHIRAM V S, DAEHN G S. Enhanced Formability of Interstitial Free Iron at High Strain Rates[J]. Scripta Metallurgica Et Materialia, 1992, 27(12): 1783-1788.

[3] QIU Li, WANG Bin, ABU-SIADA A, et al. Research on Forming Efficiency in Double-Sheet Electromagnetic Forming Process[J]. IEEE Access, 2020, 8: 19248-19255.

[4] LI Jian-jun, WEI Qiu, HUANG Liang, et al. Gradient Electromagnetic Forming (GEMF): A New Forming Approach for Variable-Diameter Tubes by Use of Sectional Coil[J]. International Journal of Machine Tools and Manufacture, 2018, 135: 65-77.

[5] XIONG Qi, TANG Hong-tao, DENG Chang-zheng, et al. Electromagnetic Attraction-Based Bulge Forming in Small Tubes: Fundamentals and Simulations[J]. IEEE Transactions on Applied Superconductivity, 2017(99): 1.

[6] XIONG Qi, HUANG Hao, XIA Liang-yu, et al. A Research Based on Advance Dual-Coil Electromagnetic Forming Method on Flanging of Small-Size Tubes[J]. The International Journal of Advanced Manufacturing Technology, 2019, 102(9/10/11/12): 4087-4094.

[7] 张望, 王于東, 李彦涛, 等. 基于双向电磁力加载的管件电磁翻边理论与实验[J]. 电工技术学报, 2021, 36(14): 2904-2911.

ZHANG Wang, WANG Yu-dong, LI Yan-tao, et al. Theory and Experiment of Tube Electromagnetic Flanging Based on Bidirectional Electromagnetic Force Loading[J]. Transactions of China Electrotechnical Society, 2021, 36(14): 2904-2911.

[8] 李春峰, 张景辉, 赵志衡, 等. 胀形用集磁器的实验研究[J]. 哈尔滨工业大学学报, 2000, 32(4): 107-109.

LI Chun-feng, ZHANG Jing-hui, ZHAO Zhi-heng, et al. Experimental Study on Magnetic Collector for Bulging[J]. Journal of Harbin Institute of Technology, 2000, 32(4): 107-109.

[9] YU Hai-ping, LI Chun-feng, ZHAO Zhi-heng, et al. Effect of Field Shaper on Magnetic Pressure in Electromagnetic Forming[J]. Journal of Materials Processing Technology, 2005, 168(2): 245-249.

[10] QIU Li, WANG Cheng-lin, ABU-SIADA A, et al. Numerical Analysis of Tube Expansion by Electromagnetic Forming Using Magnetic Field Shaper[J]. IEEE Access, 2020, 8: 196253-196263.

[11] 黄浩. 基于集磁器的板材电磁成形校形研究[D]. 宜昌: 三峡大学, 2019: 13-16.

HUANG Hao. Research on Shape Correction of Sheet Metal Electromagnetic Forming Based on Magnetic Collector[D].Yichang: Three Gorges University, 2019: 13-16.

[12] 邱立, 杨新森, 常鹏, 等. 双线圈轴向压缩式管件电磁胀形电磁力分布规律与管件成形性能研究[J]. 电工技术学报, 2019(14): 2855-2862.

QIU Li, YANG Xin-sen, CHANG Peng, et al. Electromagnetic Force Distribution and Forming Performance in Electromagnetic Tube Expansion Process with Two Coils[J]. Transactions of China Electrotechnical Society, 2019(14): 2855-2862.

[13] 黄李阳. 基于电磁成形技术的双向加载式管件电磁脉冲焊接研究[D]. 宜昌: 三峡大学, 2020: 20-25.

HUANG Li-yang. Research on Electromagnetic Pulse Welding of Bidirectional Loading Pipe Fitting Based on Electromagnetic Forming Technology[D]. Yichang: Three Gorges University, 2020: 20-25.

[14] 邱立, 余一杰, 聂小鹏, 等. 管件电磁胀形过程中的材料变形性能问题与电磁力加载方案[J]. 电工技术学报, 2019, 34(2): 212-218.

QIU Li, YU Yi-jie, NIE Xiao-peng, et al. Material Deformation Properties and Electromagnetic Force Loading Scheme of Pipe Fitting during Electromagnetic Bulging[J]. Transactions of China Electrotechnical Society, 2019, 34(2): 212-218.

[15] 李彦涛. 基于径向-轴向电磁力加载式管件电磁翻边成形研究[D]. 宜昌: 三峡大学, 2020: 32-37.

LI Yan-tao. Research on Electromagnetic Flanging Forming of Pipe Fitting Based on Radial and Axial Electromagnetic Force Loading[D]. Yichang: Three Gorges University, 2020: 32-37.

Electromagnetic Flanging Forming Effect of Bidirectional Loading Tube Fittings Based on Magnetic Field Shaper

QIU Li1a,1b, TIAN Xi1a,2, WU Wei-ye1a, WANG Cheng-lin1a,3

(1. a. College of Electrical Engineering and New Energy; b. Hubei Provincial Key Laboratory of Operation and Control of Cascade Hydropower Stations, China Three Gorges University, Yichang 443002, China; 2. Changsha Power Supply Branch, State Grid Hunan Electric Power Company, Changsha 410015, China; 3. Materials Branch of State Grid Chongqing Electric Power Company, Chongqing 401121, China)

The work aims to propose a bidirectionally loaded electromagnetic flanging technology for tube fittings based on magnetic field shaper to solve the problem of non-ideal flanging effect due to the only loading of radial electromagnetic force during traditional electromagnetic flanging of tube fittings. A two-dimensional axial symmetry analysis model was established by COMSOL and the effects of coil structure parameters on radial and axial electromagnetic force distribution and tube flanging effect were studied. On this basis, the new loading method was compared with the traditional electromagnetic flanging of tube fittings from electromagnetic force, deformation rate and shape. The results showed that in the traditional electromagnetic flanging of tube fittings, the flanging angle can only reach 45°, while the maximum flanging angle was increased to 90° by the bidirectional loading method of radial-axial electromagnetic force. Obviously, this new loading method can achieve the expected effect and promote the development of electromagnetic flanging of tube fittings in the industrial field.

electromagnetic flanging of tube fittings; magnetic field shaper; bidirectional loading; flanging angle; driving coil

10.3969/j.issn.1674-6457.2022.03.003

TM154

A

1674-6457(2022)03-0017-08

2021-09-09

国家自然科学基金（51877122，51707104）

邱立（1984—），男，博士，副教授，博导，主要研究方向为脉冲功率成形技术、输变电设备多物理场耦合分析。