稀疏平面阵列幅相误差估计算法
2022-04-01谢婉莹金红军赵怀松
谢婉莹,金红军,赵怀松
(1.杭州电子科技大学 电子信息学院,浙江 杭州 310018; 2.中国电子科技集团公司 第五十研究所,上海 200331)
信源到达方向(Direction of Arrival,DOA)估计[1]在数字通信、信号处理和目标定位[2]方面已取得了广泛的应用[3],也是阵列信号处理的重点的研究方向。为了避免角度估计模糊,现有的阵列方案要求阵元间距小于等于入射信号半波长。这种均匀阵存在如下缺点:(1)阵元个数较多,成本高;(2)在阵元个数受限的情况,估计精度和分辨率受限;(3)阵元距离近,易受到互耦的影响,导致测向性能下降。
采用稀疏阵列[4]可以改善以上问题,但是由于阵元间距大于入射信号半波长,会产生严重的模糊问题,导致DOA估计失败[5]。传统DOA估计算法是在阵列通道间不存在幅相误差以及阵列的阵元位置误差的理想前提下展开研究的。但是在实际的工程应用中,实际的阵列流行往往会受到环境和器件本身等因素的影响而出现偏差和扰动[6]。此外,当存在阵列误差情况时,基于子空间的DOA估计算法中阵列接收数据协方差矩阵容易出现秩损,最终导致算法的估计性能严重恶化,甚至失效[7-8]。因此,在存在幅相误差时,对稀疏平面阵列的DOA估计算法展开研究可推动二维平面阵的应用与发展,具有一定的工程价值[9]。
在阵列幅相误差估计方向,文献[10]提出的辅助阵元法ISM(Instrumental Sensor Method)在无需预期阵列误差参数的条件下增加若干个已校准的辅助阵元来估计信源方位。该方法在得到信源方位准确估计的同时对阵列误差进行准确校正,完成预期阵列误差和信源方位的“去耦合”估计[11-12]。但是由于稀疏阵列的角度模糊特性,经典的ISM方法无法直接用于稀疏阵列的幅相误差估计,需要对算法进行改进,使之满足ISM算法的假设条件[13]。消除阵列的模糊特性是最直接的一种改进方式。
本文主要针对稀疏均匀平面阵列在存在幅相误差情况时的DOA估计问题展开研究[14-15]。本文将线阵下基于介质的去模糊算法推导到二维平面阵列中,解决了平面阵列的测角模糊问题,同时将ISM校正算法与该算法相结合,改善了ISM方法不适用于稀疏阵列的缺陷,提高了算法的适应性。
1 阵列信号模型及模糊性分析
1.1 存在幅相误差的信号模型
一个均匀矩形平面阵列由M×N个阵元组成,其中阵元的位置为(xi,yi),其x轴和y轴上的阵元间距分别为dx和dy。入射信号从K个不同的方向以角度(θk,φk)(k=1,2,…,K)入射。此时,该阵列中第k个信号阵列流行为
(1)
(2)
式中,i和j分别表示为在x轴和y轴上的第i个阵元和第j个阵元;A为阵列流行矢量形式;β=2π/λ为波数;θ∈[0,π];φ∈[0,2π]。当存在幅相误差时,设阵元(xi,yi)的幅度误差为μij,相位误差为φij。原点处阵元没有误差,将其做为参考阵元,幅相误差矢量可表示为
Γ=[1Γ2…ΓM×N]=
[1μ2exp(jφ2)…μM×Nexp(jφM×N)]T
(3)
存在幅相误差时,阵列流行可表示为
(4)
此时阵列的接收信号表示为
(5)
式中,阵列接收信号是X(t)和S(t)是空间入射信号,S(t)=[S1(t),S2(t),…,Sk(t)];N(t)=[n1(t),n2(t),…,nk(t)]为天线阵列接收到的噪声。
1.2 传统ISM幅相误差估计算法
ISM幅相误差校正算法是一种基于接收数据矢量的单辅助信源校正算法,该算法不受阵列结构的限制,运算量较小,在参数估计算法中没有局部收敛问题,易于工程实现,估计效果好[13]。其基本原理描述如下:
在M×N个阵元的平面阵列中,假设有S个信号源,入射方向为(θk,φk)(k=1,2,…,S),利用在平面阵列中加入R(R≥S+1)个精准校正过的辅助阵元共同组成新的接收阵列,阵列的阵列流行矩阵A=[W(θ1,φ1),W(θ2,φ2),…,W(θk,φk)]。其中,W(θi,φi)为第i个信号源的导向矢量。
W(θ,φ)=Γ(θi,φi)a(θi,φi),i=1,2,…,S
(6)
前R个精准校正过的辅助阵元对应的幅相误差值为1,将导向矢量a(θi,φi)和幅相误差对角矩阵Γ(θi,φi)分块得到
(7)
式中,前R个精准校正过的阵元对应的导向矢量为a1(θ,φ),后M×N-1个存在幅相误差阵元对应的导向矢量为a2(θ,φ),进一步可得
(8)
根据子空间算法原理可知
(9)
将式(8)代入式(9)有
(10)
δH(θi,φi)Q(θi,φi)δ(θi,φi)=0
(11)
(12)
其中,(θ,φ)≠0。当满足Q(θ,φ)出现秩损或为奇异阵时,ISM算法才能实现信源DOA估计参数和阵列幅相误差的联合估计,如下式所示。
(13)
(14)
(15)

2 基于介质的模糊抑制算法
2.1 基于介质的线阵模糊抑制原理
在稀疏线阵下加有介质基片的去模糊原理[16],主要思想在于引入介质,借用电磁波在介质中的折射改变原有的路程差,使得阵元位置发生变化,得到新的阵列流形A2,并用A2取代原来的A,达到去除角度模糊的效果。线阵下的具体原理和结论如下图所示。

图1 矩形介质放置在线阵的结构图Figure 1. The structure diagram of the rectangular substrate placed on the line array
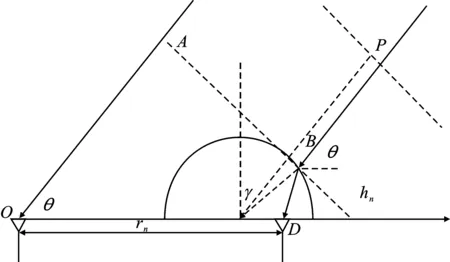
图2 半球介质放置在线阵的结构图Figure 2. The structure diagram of hemispherical substrate placed on line array
平板介质的等效位置
(16)
半圆介质的等效位置
rn.E=(rncosθ+Δrn(θ))/cosθ
(17)
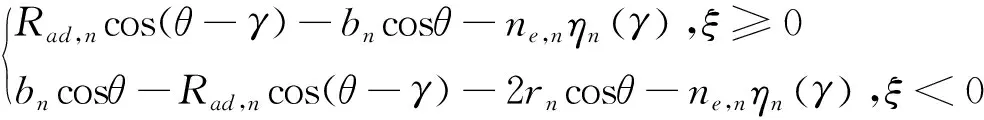
(18)
2.2 线阵至面阵的推广
本文将线阵下的介质去模糊算法推导应用在二维空间下的稀疏平面阵列中[17],如图3所示,假设将一个矩形介质块放置在阵列的第n个阵元上,该阵元位置为P(xn,yn),折射率为ne,介质块厚度为hn,(θ,φ)是某一入射信号的入射角,其中θ是入射信号的俯仰角,f是入射信号的方位角,并且该入射信号在介质块中的折射角为γ,rn(θ,φ)是第P个阵元在入射角为(θ,φ)下的等效位置。直线A’Q’存在并与A’O入射信号垂直的平面为该入射波的波前。入射波在传入到该平面之前都是等相位的,当传入到Q’点后,入射波继续在介质块中传播Q’P段才能达到第P个接收阵元,并且入射波入射到波前中的A’后在自由空间继续传播A’O段到达参考阵元O,因此根据波程差关系和两者的传播路程求得等效位置rn(θ,φ)。

图3 矩形介质放置在平面阵的结构图Figure 3. The structure diagram of the rectangular substrate placed on the plane array
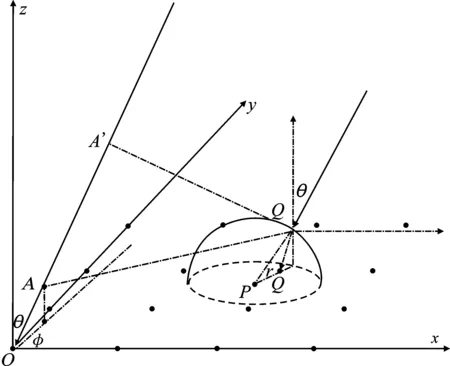
图4 半球介质放置在平面阵的结构图Figure 4. The structure diagram of hemispherical substrate placed on plane array
因此,由图3推导得到入射信号入射到P阵元和参考阵元的波程差Dn。
(19)
由平面阵列中空间第i个阵元与参考阵元之间的波程差可得Dn=Δx。
Δx=2π(xicosφsinθ+yisinφsinθ)/λ
(20)
与线阵的情况不同,求解发现平面阵阵元等效位置结果并不唯一。为简化运算,本文选取一个特殊结果作为等效位置点rn(θ,φ)(xn′,yn′),即加入平面介质后该阵元的等效位置为
(21)
同理,参考图4分析半圆介质的抑制原理,经过推导得到
nebnsinγ-sin(θ-γ)ηn(γ)=0
(22)
(23)
求解方程式(22)得到γ值,再将γ值代入式(23)可得Dn,同时再代回到式(21)可以得到加入半圆介质后该阵元的等效位置。
通过上面的推导可以获得添加介质处的阵元等效位置,从而得到抑制模糊阵列流行矢量AS,但是该方法的抑制效果会受到介质参数的影响[18]。为了获取最佳的抑制效果,就需要获取合适的介质参数,本文以矩形介质为例,参数有介质高度h和介质折射率ne。定义抑制度J的表达式为
(24)

(25)
算法描述如下:
步骤1在稀疏阵列前选择一个或若干个阵元,在介质约束条件内求解抑制度J最大的介质高度和折射率。在选定的阵元前面加入对应的介质;
步骤2对等效阵列流形矢量利用ISM方法进行幅相误差估计,此时估计的结果是加介质后的等效误差;
步骤3根据真实阵列流形和等效阵列流形的转换关系对ISM估计的等效误差进行反变换,求得阵列的真实幅相误差。
3 仿真与分析
3.1 存在幅相误差下的DOA估计分析
本文的仿真条件为:在6×6的平面阵列中,以位于(0,0)处的阵元为参考阵元,所有距离单位都为半个波长大小,阵元间距为1个波长,信噪比为20 dB,快拍数为1 000,入射信号源方向为(48°,48°)。当加入介质时,介质折射率为3,高度为2。
由图5(a)可以看出,传统Music算法估计稀疏阵列会产生伪峰,即角度(132°,48°)方向。图5(a)和图5(c)的对比显示,基于介质的方法能够对伪峰进行抑制。由图5(b)和图5(c)结果对比可以发现,幅相误差会降低谱峰并使谱峰偏移,同时降低伪峰抑制效果。
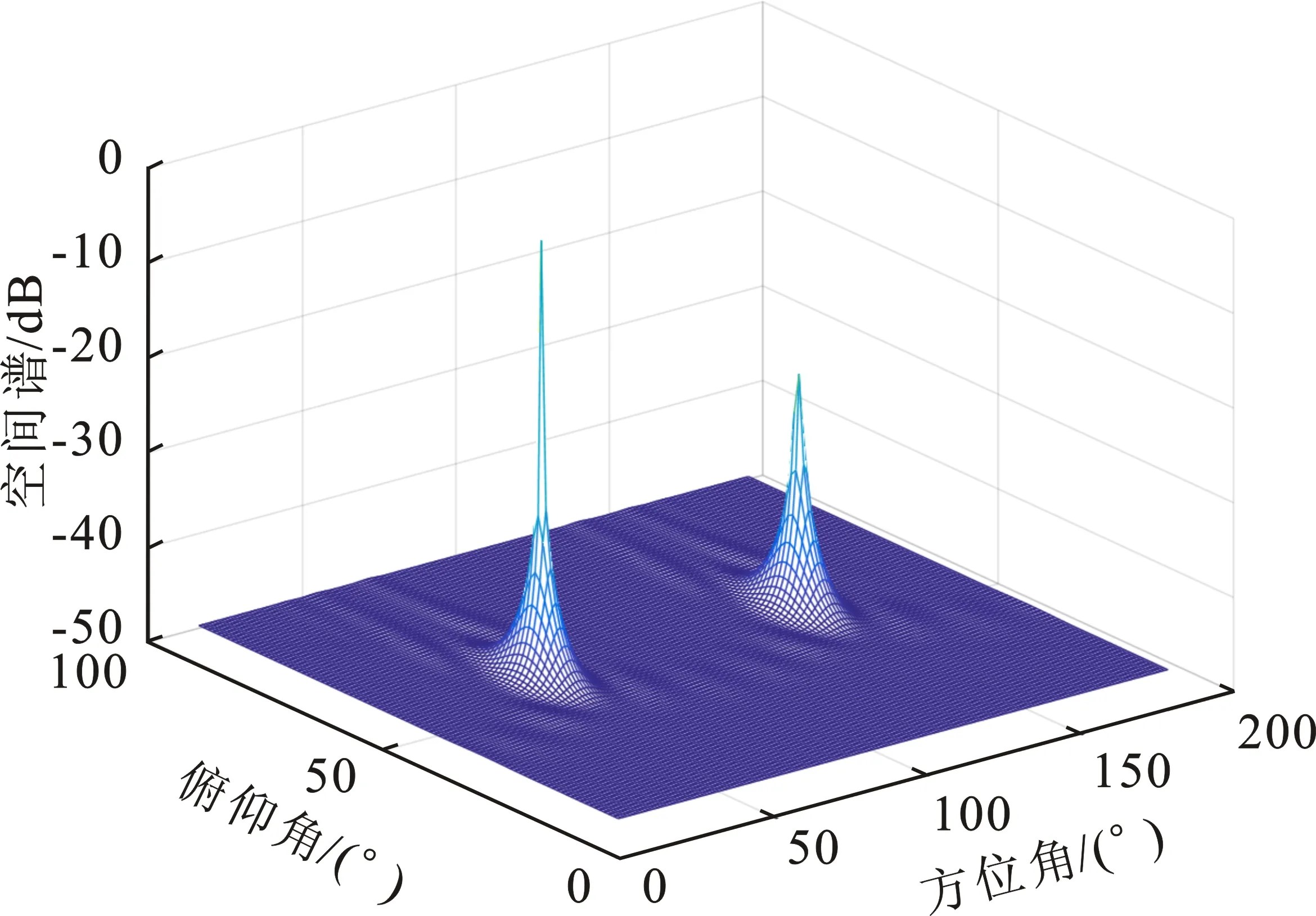
(a)
3.2 介质去模糊算法信噪比分析
由图6和图7可知,基于介质的二维平面DOA估计去模糊算法在二维方向的估计精度随信噪比的增加而相应提高,且俯仰面的估计误差要比方位面小,方位角最大误差为22°,而俯仰角最大误差仅为1.3°。因此在进行DOA估计时,俯仰角相对于方位角的估计精度更高,表现更加优越。
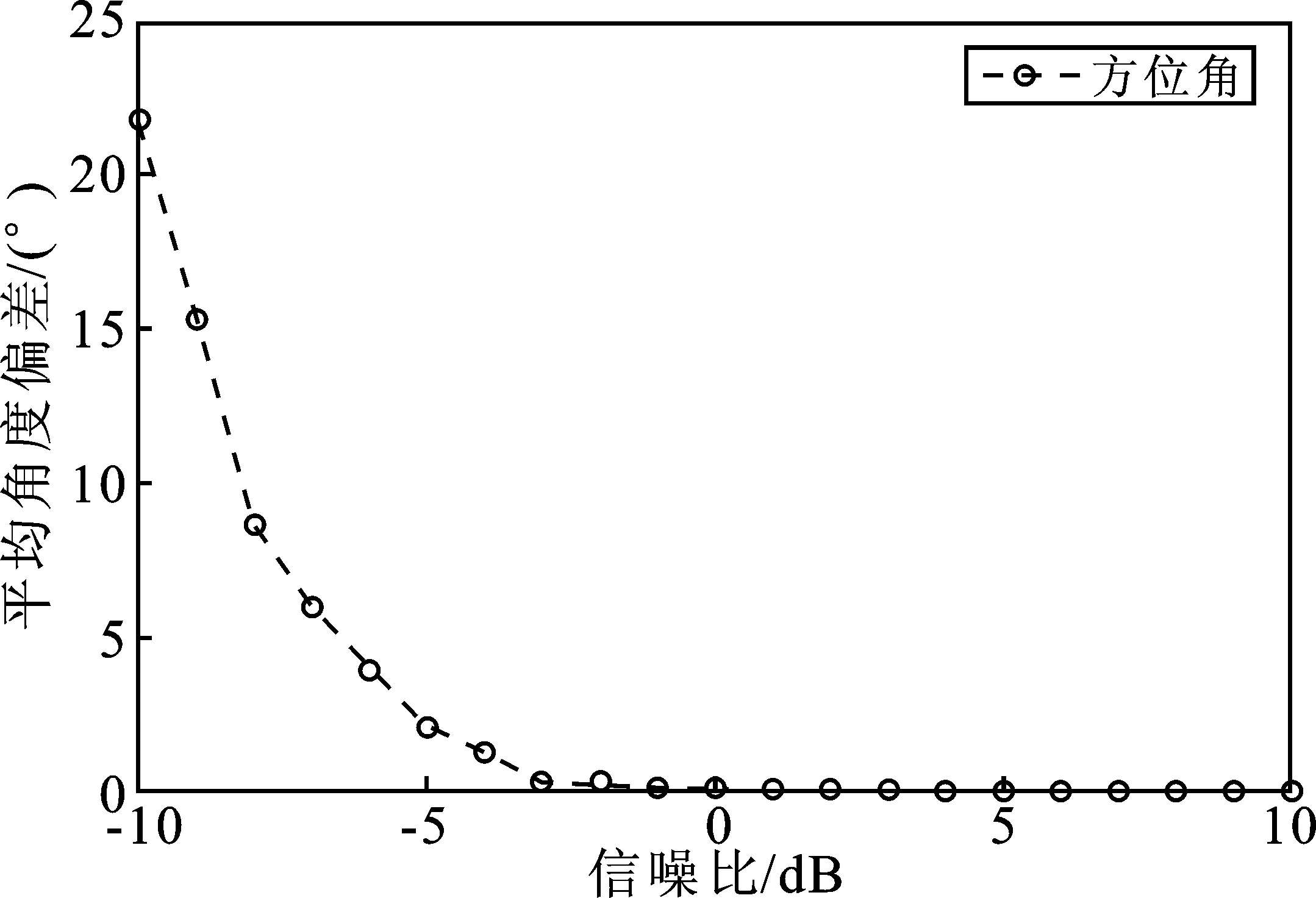
图6 方位面均方根误差与信噪比的关系Figure 6. The relationship between root mean square error and signal-to-noise ratio in azimuth plane

图7 俯仰面均方根误差与信噪比的关系Figure 7. The relationship between root mean square error and signal-to-noise ratio in elevation plane
3.3 矩形介质下参数的性能分析
在章节3.1的仿真条件下,针对矩形介质下的平面DOA估计去模糊算法,考虑到相关参数高度h和折射率ne,进一步分析参数对该算法性能的影响。通过改变高度和折射率来控制抑制度的表现,得到该算法下高度、折射率与抑制度的三维关系,如图8所示。
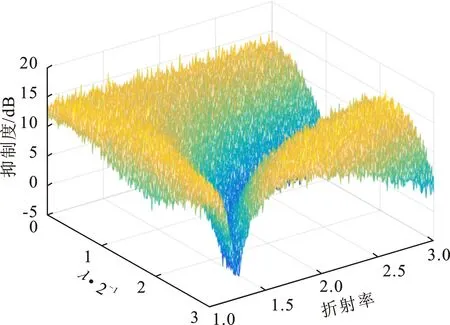
图8 矩形介质下高度、折射率和抑制度三维关系图Figure 8. Three-dimensional relationship diagram of height,refractive index and suppression under rectangular substrate
从图8可知,在基于矩形介质的二维平面DOA估计去模糊算法中,介质的高度和折射率同时 于抑制模糊。在参数选取范围下,图中存在一道明显的凹槽,此时该算法的效果最差,抑制度最小,无法抑制模糊假角。在凹槽以外的范围中则存在3种情况:(1)当高度范围为0~0.5,此时无论折射率如何取值,该算法都能有效抑制假角;(2)当折射率范围为1~1.4,高度取任意大于1的值也能有效抑制假角;(3)当高度在1.8~2.7,折射率在1.6~3的范围内,此时抑制度达到最大,模糊消除达到最佳效果。此外,由图可知该方法下抑制度最大可达到17 dB左右。
3.4 基于介质算法下的ISM幅相误差校正
ISM算法无法被直接应用在稀疏面阵的幅相误差估计中。本文在章节3.1的平面阵列中加入7个校正阵元构成新的阵列。ISM算法与介质DOA估计算法相结合后得到的阵元幅相误差情况如图9所示。

(a)
从图9可以看出ISM算法与介质DOA算法进行结合改进后能准确估计出相位误差和幅度误差值。图10则说明该算法的均方误差随着信噪比增大逐渐减小,即改进的适合稀疏平面阵的算法估计效果良好。

图10 幅相误差估计算法均方根误差与信噪比关系图Figure 10. The relationship between the root mean square error and the signal-to-noise ratio in the amplitude-phase error estimation algorithm
4 结束语
针对传统ISM幅相误差估计算法无法直接应用在稀疏面阵中的问题,本文将基于介质的模糊抑制算法引入ISM算法中,保证了算法的成立条件。将基于介质的稀疏线阵DOA估计算法推广至面阵,并分析了矩形介质抑制模糊的算法原理及矩形介质相关参数折射率和高度对抑制度的影响。通过本文的方法可以获取抑制度最大的参数。仿真结果表明该方法对模糊角度的最大抑制可达17 dB。然后,将ISM方法的阵列流行矢量替换为本文推导的流行矢量,获得了良好的幅相误差估计效果,表明该方法具有一定的实际应用价值。
