基于受激布里渊散射的光子辅助瞬时测频方案
2022-04-01刘可欣高娜
刘可欣,高娜
(河南理工大学物理与电子信息学院,河南焦作454003)
0 引言
传统的电子瞬时测频技术(Instantaneous Frequency Measurement,IFM)在信号的带宽和测量的实时性等方面都有一定的局限性。由于微波光子学的发展,将信号转换至光域进行处理和分析,实现了大带宽、低损耗、抗干扰等优良性能,为微波信号的实时监测提供了可能[1]。
已经有很多IFM 方案被提出,主要有频率-幅度映射型、频率-时间映射型、光信道化等。频率-幅度映射可分为:频率到光功率的映射[2-4]和频率到微波功率的映射[5-9]。这种方案是将微波信号调制至光域,在光域进行一系列处理后,经探测器检测输出功率,实现频率到功率的映射,从而建立功率的幅度比较函数(Amplitude Comparison Function,ACF),得到ACF 与待测微波信号的关系,最终获得待测微波信号的频率。频率-时间映射型方案[10]通过光域扫描或者光域傅里叶变换将待测微波信号的频谱信息转为时间信息,进而从探测电信号的时间信息估测出频谱信息。在频率-空间的映射方案[11-15]中,把微波的频率信息转换成空间位置上的分布,这个过程也称为信道化。把微波信号加载至光域后,通过不同的光器件,例如:光学频率梳[11-13](Optical Frequency Comb,OFC)、标准具[14](Etalon)、光纤布拉格光栅(Fiber Bragg Grating,FBG)等,将频率映射到空间上,根据空间的分布信息,得到待测微波的频率。
有关测量多个频率的方案大多和扫频、信道化有关。受激布里渊散射(Stimulated Brillouin Scattering,SBS)由于其较窄的布里渊增益带宽被广泛应用于频率到空间的映射方案中。文献[13]提出了一种基于波长扫频和受激布里渊散射的频率测量方案。将待测微波信号经调制器调制到上路光载波上作为泵浦光,当泵浦光与经过扫频信号相位调制的下路光波之间相差一个布里渊频移量时发生SBS,经光电转换后测得调制信号的峰值,最后计算出微波信号的频率。该方案可测频范围为0.5~27 GHz,测量误差为30 MHz。扫频需要在测量范围内有精细的扫描步长,因此在时间上有延迟,且可能会遗漏某些突发性的信息,达不到瞬时测频的要求。有关信道化的方案,文献[15]提出了一种基于频谱控制受激布里渊散射的改进信道特性的光子辅助微波信道化器[15]。通过将激光阵列多路复用,再分裂为两路,一路被待测微波信号调制,一路被用作泵浦来激发SBS。最后实现了一种可调谐的微波信道化器,该方案需要多个激光器,增加了系统的复杂性,系统成本较大。
本文为实现大带宽范围内任意频率的测量,提出了一种IFM 方案,将经待测微波信号调制后的光信号作为泵浦,与光频梳作用产生布里渊散射,从而实现了待测信号到空间的映射,相比于采用激光阵列激发SBS 的方案,本设计减少了所需激光器的数量。微波调制后的光信号和OFC 各自分路后送入相应的色散位移光纤中,因此避免了各个信道间的串扰。整个系统只需要一个激光器,便可实现光载波调制和光频梳的产生,利用光频率梳来替代激光阵列,不需要进行扫频,可实现在一定带宽范围实时测频,通过仿真实验证明了该方案的可行性和可靠性。
1 原理
该方案的系统结构如图1所示。
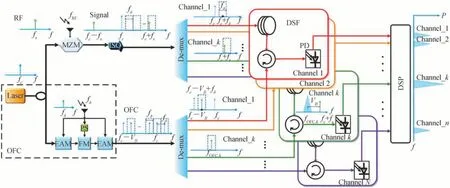
图1 基于受激布里渊散射的光子辅助瞬时测频系统Fig.1 Photon-assisted instantaneous frequency measurement system based on stimulated Brillouin scattering
整个系统由上下两部分组成,由同一个连续激光器(CW Laser)发出光信号,经1×2 光分路器按1∶2 的功率比分为两条支路。上路用作本地载波,下路用作生成OFC。上路光信号注入MZM,被待测微波信号进行抑制双边带载波调制。系统中插入光隔离器,用于隔离光梳经由光环形器、色散位移光纤、分路器传送过来的信号,以免影响CW 激光器的正常工作。信号经解复用器(Demultiplexer)后被分为N路送入信道中,作为受激布里渊的泵浦。下路生成光频率梳,经分离后也被分为N路,与上路一一对应,经光循环器送入通道中,在色散位移光纤(Dispersion Shifted Fiber,DSF)中产生受激布里渊散射,再经光循环器输出,反应后的信号注入光电探测器(Photodetector,PD)中进行光电转换。若上路信号的第k个通道中被滤出待测微波信号,则会在DSF 中作为泵浦与下路的光频率梳发生受激布里渊散射,此时会产生受激布里渊增益,则该通道输出的功率会有明显的增大,经数据处理后得到待测微波信号的频率。
假设CW 激光器输出的激光信号为

式中,E0为单频激光器的输出激光幅度,ωc为激光信号角频率,ωc=2πfc,fc为激光信号频率。
待测微波信号为

式中,En(n=1,2,3...)为待测微波信号包含的各个频率的幅度,ωn(n=1,2,3...)为待测微波信号包含的各个角频率。
双驱动MZM 进行抑制载波的双边带调制,且工作在推挽模式下,此时调制器只会实现强度调制,当输入射频信号为单频信号时,MZM 的输出为


式中,ΔVB为布里渊线宽。
只有当泵浦功率满足SBS 的阈值光功率时才会产生受激布里渊增益,SBS 的阈值光功率Pth可由式(12)给出为

式中,gB为峰值增益系数,Aeff为纤芯有效面积,Leff为有效作用长度。
当引入上路泵浦光时,由于发生了受激布里渊散射,在低于fP一个VB的位置产生一个增益谱,在高于fP一个VB的位置会产生损耗谱。
将上路光信号和下路光频率梳信号分离,上下两部分各分出N路信号,将两部分的N路信号一一对应,如图1所示,经光循环器可组成N个信道,每个信道中调制光信号和频梳的频谱关系如图2(a)所示。
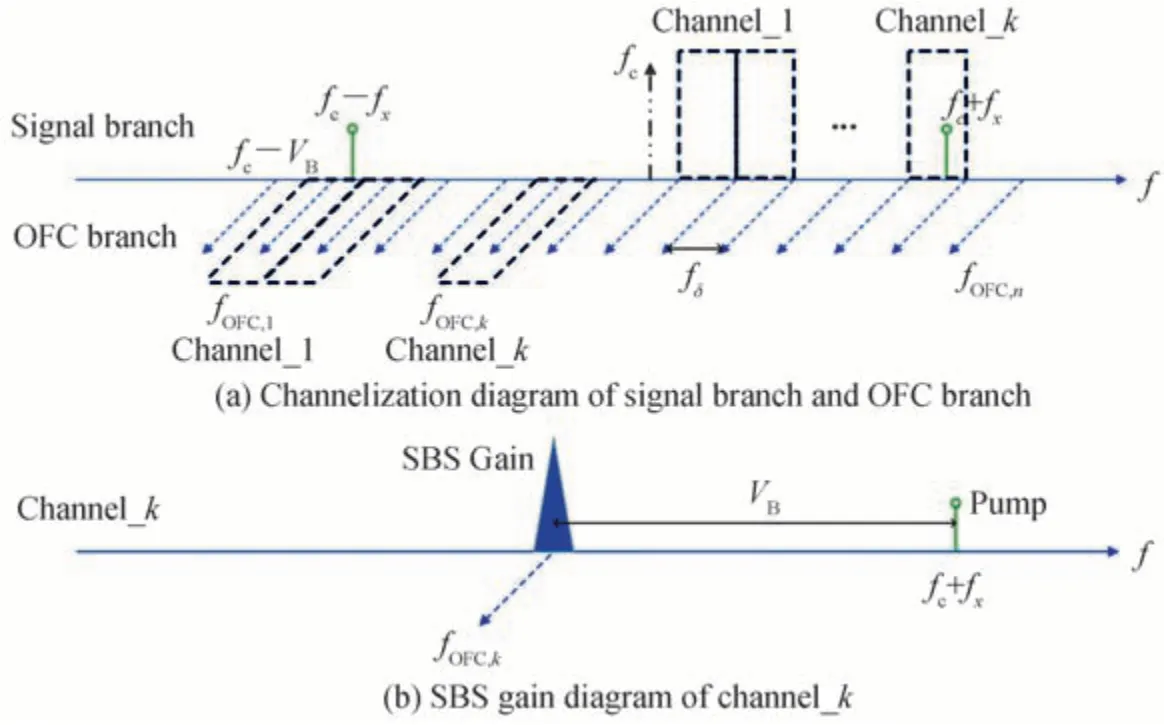
图2 信道化频谱示意图Fig.2 Schematic diagram of channelized spectrum
若两路信号发生了受激布里渊散射且输出到第k信道,如图2(b)所示,则第k个信道的中心频率与泵浦的中心频率fP的关系为

若

则微波信号频率fx可表示为

式中,fδ为信道的带宽。
若上路信号的待测微波信号在第k个信道被滤出,则在第k个信道中将会发生受激布里渊散射,此时产生一个受激布里渊增益,则该路信道经PD 转换后会检测出功率有明显的增益。由式(15)可计算出该信道中的微波频率,该系统的分辨率为信道带宽,频率误差为该信道带宽的一半。
2 实验与结果
为了验证方案的可行性,利用optisystem 光学仿真软件进行仿真实验。设置激光器中心频率为193.4 THz,线宽为3 MHz,输出功率为25 dBm。激光信号经光分路器按1∶2 的功率比分为两条支路。待测微波信号通过MZM 对光信号进行抑制载波的双边带调制。双驱动MZM 的半波电压Vπ设为4 V,开关偏置电压Vbias设为4 V,开关射频电压Vπ,dc设为4 V,偏置电压1vbias1设为2 V,偏置电压2vbias2设为-2 V,此时MZM 工作在最小偏置点。本系统中布里渊频移量VB=10 GHz。
本IFM 系统既可以测量单一频率也可以测量多个频率。系统中插入光隔离器,确保系统后半部分反应的光波不会影响到前面激光器的运行。将经过隔离器的信号送入分离器中进行滤波,N个通道的中心频率从本系统中激光器中心频率fc+fδ=193.400 1 THz 开始,以fδ=0.1 GHz 为间隔进行滤波。滤波的通道数是决定该系统测量范围的因素之一。上路光信号被分离器解复用后分别送入N个信道中,与下路送来的信号进行受激布里渊散射。
根据图1,调节OFC 模块的RF 信号为0.1 GHz,使OFC 产生频率间隔为0.1 GHz 且平坦的光梳信号。将OFC 信号送入分离器,分离器的各个通道从fc-VB+fδ=193.390 1 THz 开始,同样以0.1 GHz 为间隔进行滤波,将产生的N个信号送入与上路对应的信道中。上下两路信号经解复用后在色散补偿光纤中相遇,若上路的某个信道中含有待测微波信号,则该信道将会发生受激布里渊散射,产生受激布里渊增益。
2.1 单频测量
当测量频率为单频时,设待测微波信号为20 GHz。为了节省时间和减小计算量,在仿真时选择5个信道观察。从上路滤出的五个信号的中心频率分别为193.419 8 THz、193.419 9 THz、193.42 THz、193.420 1 THz、193.420 2 THz,依次以0.1 GHz 为间隔递增。从OFC 中滤出的五个信号的中心频率为193.409 8 THz、193.409 9 THz、193.41 THz、193.410 1 THz、193.410 2 THz,依次以0.1 GHz 为步长递增。同时送入色散位移光纤后,输出光功率如图3所示。

图3 单频信号的SBS 响应Fig.3 SBS response of single frequency signal
如图3所示,第三个信道的输出功率明显高于其他四个信道,通过放大后可以看出,第三信道的输出光功率为1.36 dBm,其他四个信道的光功率与第三信道比最多相差了27.6 dBm,最少相差了17.94 dBm。通过上述原理可知,第三信道内有SBS 发生,意味着送入此信道内的上路光信号中包含有待测微波信号,此信道的中心频率为193.42 THz,可得待测微波信号的频率为20 GHz。
2.2 多频测量
当待测微波信号为多个频率时,设射频信号f1为10 GHz、射频信号f2为12 GHz,从上路滤出信号的中心频率从193.409 5 THz 开始,以0.1 GHz 为间隔依次递增至193.412 5 THz。从下路滤出信号的中心频率从193.399 5 THz 开始,以0.1 GHz 为间隔依次递增至193.402 5 THz。同时送入色散位移光纤后,输出光功率如图4所示。
如图4所示,信道a和信道b中的输出光功率分别为-5.108 56 dBm、-4.744 49 dBm,其他信道最高的光功率为-17.8 dBm,由此看出信道a和信道b光功率明显大于其他信道,经PD 转化为电功率后分别为-40.359 dBm、-29.632 dBm。由此可见,这两个信道中有待测微波信号。由实验可知a=100,b=120,根据式(15)可推出待测微波信号的频率分别为10 GHz、12 GHz。
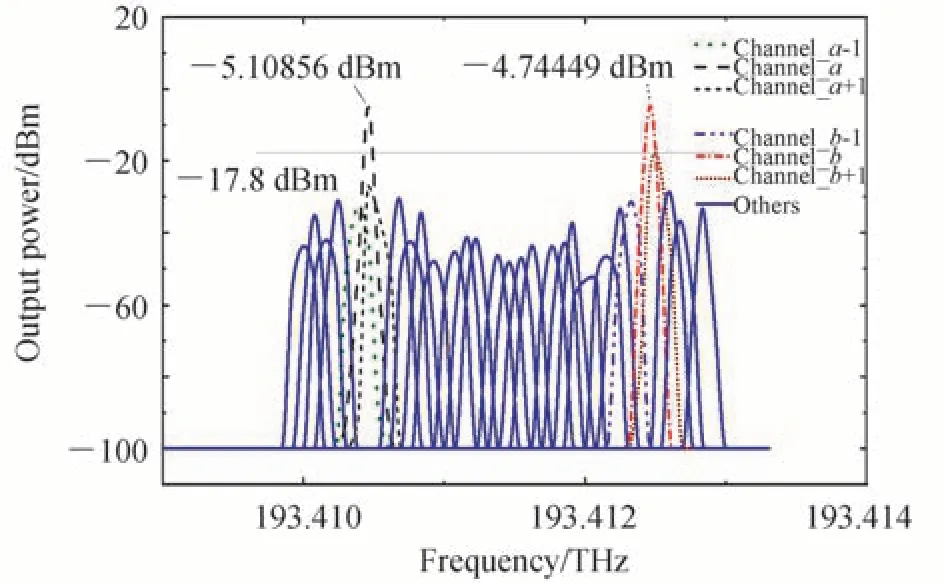
图4 多频信号的SBS 响应Fig.4 SBS response of multi-frequency signals
本文研究的瞬时测频方法采用信道化方式直接检测,通过检测每个通道经PD 后的输出功率值从而判断出待测微波信号的频率。根据实验结果可知,含有微波信号的信道输出功率比相邻两信道输出功率高出约20 dBm 以上,由此判定,该通道内有信号。
2.3 测量误差
选取8~10 GHz 的待测微波信号分别送入该系统。当待测微波信号以0.1 GHz 为步长,频率依次增送入系统时,待测微波信号的频率与测量结果的关系如图5所示,测量值与理论值完全相同,没有误差。当待测微波信号以0.01 GHz 为步长,频率依次递增时,输入微波信号频率和测量出的微波信号频率的关系如图6所示。从图中可以看出,仅当输入频率是0.1 GHz 的整数倍时,输入频率与测量频率相同,其它频率都和输入频率有些许误差。测量误差如图7所示,误差范围在-0.05~0.05 GHz,当输入频率是0.1 GHz 的整数倍时误差值为0 GHz。

图5 分辨率为0.1GHz 时的测量结果Fig.5 Measurement results at a resolution of 0.1GHz
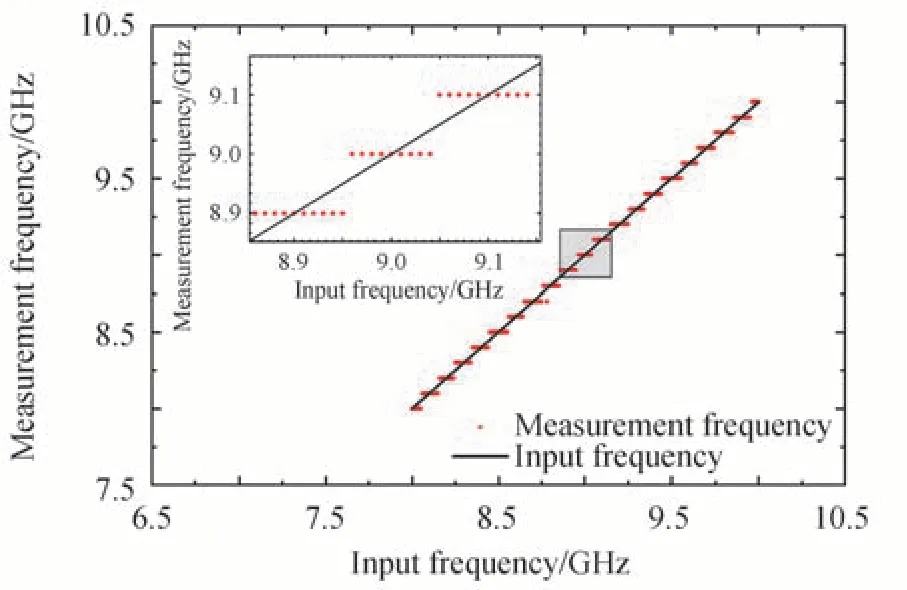
图6 分辨率为0.01GHz 时的测量结果Fig.6 Measurement results at a resolution of 0.01GHz
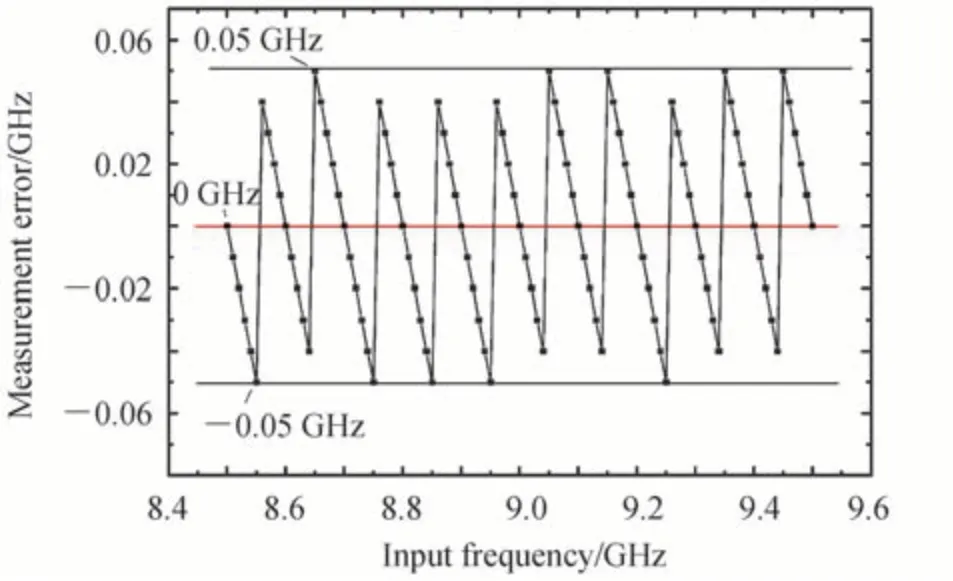
图7 测量误差Fig.7 Measured errors
根据以上测量结果可知该系统的测量分辨率为0.1 GHz,若测量分辨率小于0.1 GHz 时,将会引起测量误差,测量误差为-0.05~0.05 GHz。
测量误差来源于信道带宽fδ,即解复用器的波长间隔。由图2 可以看出,当信号频谱落在通道内时,不管处于通道内的哪个位置,根据本系统的计算原理,都将会按照落在通道中间位置来计算。本测频系统设置的通道带宽为0.1 GHZ,所以当信号频谱落在通道左侧时测量误差为-0.05~0 GHz,落在通道右侧时测量误差为0~0.05 GHz。若想减小该测量系统的误差,则需要波长间隔更小的解复用器。根据现在的研究,超密集波分复用技术正在逐步发展,有望研究出波长间隔更小的波分复用器件。
由于MZM 有固定的带宽,该方案选取的MZM 的带宽为25 GHz,该数值即为测量范围的上限值。
3 影响因素分析
本方案采用马赫增德尔调制器进行电光调制,将微波信号调制至光载波上进行抑制载波的双边带调制。但在现实应用场景中,MZM 会因温度、制作工艺不完善等问题发生偏置点的漂移。偏置点的漂移将导致载漏、输出光功率减小和倍频信号的产生,这些因素通常都会影响测量的准确性。正常的偏置电压为4 V,当偏置电压发生漂移时,有信号的通道channel_k与其相邻信道的输出功率将会发生变化,如图8所示。
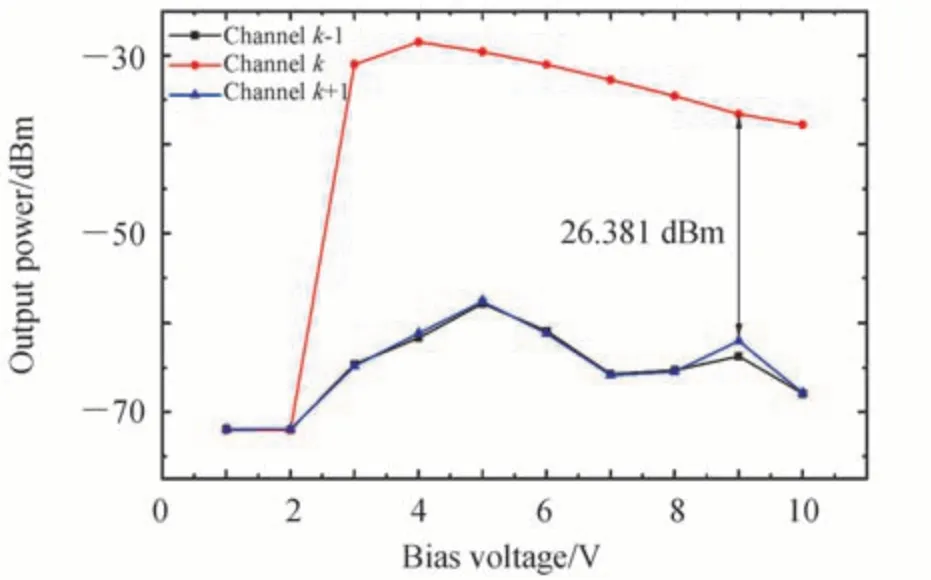
图8 偏置点漂移的影响Fig.8 The influence of the bias point drift
由图8 可以看出,偏置电压为4 V 时,信道k输出功率最大,且远远大于相的输出功率,此时可正常测得微波信号。当偏置电压小于3 V 时,信道k的输出功率与相邻信道的输出功率大致相同,此时测不出微波信号。当偏置电压大于4 V 时,信道k的输出功率不断下降,但至少大于相邻两信道26.381 dBm,此时也可测得微波信号。从测量结果来看,只有在偏置电压小于3 V 时,该方案检测不到微波信号,说明该方案在一定程度上能够对偏置电压的漂移起到抑制作用。为了进一步减小偏置电压对测量结果准确性的影响,需应用偏置点稳定控制技术来保证该方案的稳定性。
该方案测量范围的上限受调制器的带宽限制,采用带宽更大的调制器即可增大测量范围。
4 结论
本文提出了一种基于受激布里渊散射的光子辅助测频系统,由单个激光器提供光源,分两路后,一路作为光载波由待测微波信号调制,一路用于生成多个高平坦度、等间隔的光频率梳,各自送入对应的色散位移光纤,结合受激布里渊散射效应,可以测量从0.1 GHz 到25 GHz 的多个瞬时微波频率信号,测量分辨率为0.1 GHz,测量误差为±0.05 GHz。此外还分析了马赫增德尔调制器偏置电压漂移对测量结果的影响,仿真结果表明当偏置电压发生负向漂移时,对检测结果影响较大,但发生正向漂移时,在含有待测信号的信道中布里渊增益仍明显高于无信号的信道,说明此方案对偏置点漂移带来的影响有一定抵抗能力。利用光子辅助法,可在大频段范围内实时测得微波频率,频率测量范围宽、抗电磁干扰能力强,在电子战系统中有广阔的应用前景。