基于高斯-多项式拟合的FBG解调

邓文舫

（安徽理工大学 电气与信息工程学院 安徽省淮南市 232001）

在进行矿山钻井等工程活动时，需要对地下水的温度和压力进行监测以保证工程安全。针对这一特殊应用场景和复杂的环境，传统电学传感器易受到干扰不能正常工作。而光纤布拉格光栅(FBG)传感器能够在各种复杂的电磁环境下正常工作，且具有精度高、灵敏度高、体积小易于复用的优点，还可以组成传感网络实现多点的实时监测。

FBG 通过对入射和反射光的中心波长位置进行比较，将监测的物理量用偏移量大小来进行反映，因此需要针对传感器设计并搭建相应的解调系统，进行波长解调找出中心波长的位置，再通过中心波长偏移量与温度和压力的关系得出物理量的值[1-3]。同时目前波长解调的主流方案为非平衡M-Z干涉法[4]、光源波长扫描法[5]、CCD 分光仪法[6]等，而可调谐激光法[7]相较于前几种方案结构简单、易于实现且解调精度高，稳定性好。

解调系统实现的关键一方面在于设计出高精度、高速度的算法进行光的波形曲线拟合，另一方面在于得出偏移量和物理量之间的关系实现由光信号到物理信息的直观体现。目前常用的解调系统寻峰算法为一般包括了直接比较法[8]、中心法[9]、高斯拟合法[10]、多项式拟合法[11]等。寻峰算法能直接影响FBG 的解调速度和精度，为此首先研究了几种解调算法的特点，并进行了模拟和仿真分析。对各个算法进行了原理阐述，而后将两种算法相结合的方式设计了一种新的算法。

基于可调谐激光器的波长解调方案，采用FPGA 进行主要的运算和控制步骤完成寻峰算法的计算和分析进行仿真模拟并在搭建的系统平台进行了实验论证和测量，以及数据文本的导出，实现了针对FBG 的高精度的快速实时解调。

1 解调原理

基于可调谐激光器的解调系统的硬件结构如图1所示，主要分为电路和光路两个部分，其中光路部分按着光信号的传播依次为激光器、分光器、耦合器、传感器、光电转换器，电路部分主要包括光电转换、AD 转换、算法处理和控制以及光源的驱动，其中的控制处理部分采用的FPGA 作为主控制器。在工作时激光器按一定输出一定间隔（设定间隔为20 pm）输出波长不同的光波，然后经过AD 转换后的采样数据绘制成为散点图，再对这个散点图进行曲线拟合，并使用寻峰算法实现波长解调。

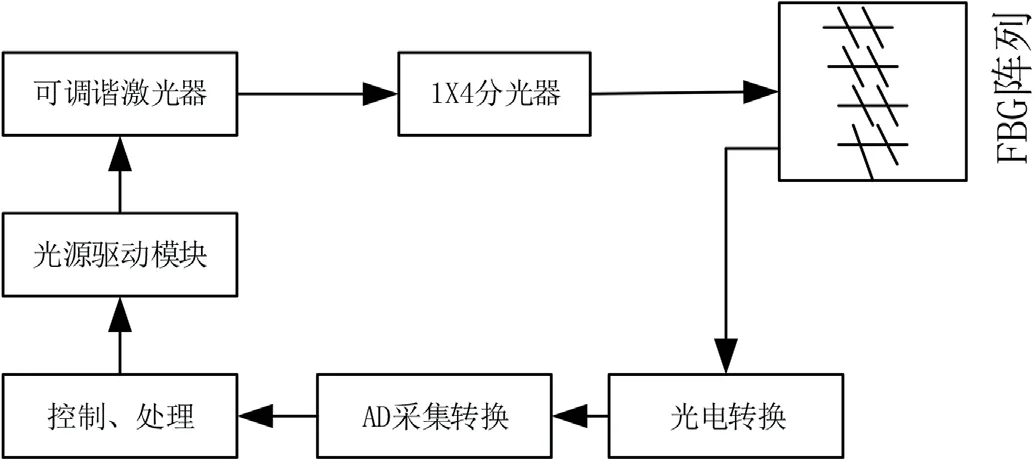
图1：解调系统结构框图

1.1 FBG的工作原理

光纤布拉格光栅的反射条件为[12]：

公式（1）中的各项参数代表光反射的布拉格条件，其中Λ 为光栅的栅格周期，λB为中心波长，ne为有效折射率。对公式（1）微分可得：

公式（2）中，ΔλB表示中心波长的偏移量；Δne表示光栅折射率的变化量，ΔΛ 表示栅格周期的变化量。外界物理参数值的大小发生变化会使其栅格周期和有效折射率变化，从而导致ΔλB也发生变化，对这个偏移量的大小计算后，就可以测出温度和压力。

温度对栅格周期和有效折射率的关系表示为：

公式（3）中ΔT为外界温度的改变量；αΛ为光纤的线性热膨胀系数，为热光系数，它们可视作常数。将式（3）带入式（2）中变换，可得温度系数：

公式（4）中，KT表示灵敏系数，这也表示中心波长的偏移量与温度的变换存在线性关系。

应力对FBG 的栅格周期和有效折射率的影响表示为：

公式（5）中，P代表弹光系数、b 为系数，ε为轴向应变。所受压力和波长偏移量的关系为：

同时，在温压监测中，还需要设置温度和压力补偿，调节温度和压力的零点，避免相互干扰。对反射波长变换的计算，就可以进行针对光波长与温度和压力的标定，将波长的偏移量转化为温度和压力进行显示。

1.2 寻峰算法

反射光谱经过光电转换和AD 转换后，得到了采集数据，需要采用寻峰算法进行曲线拟合并进行中心波长位置锁定，对几种算法原理介绍和分析后，为提高拟合精度，采用高斯多项式拟合算法。

1.2.1 直接比较法

直接比较法是利用前差公式或后差公式[13]，在进行作差并和一阶微分后找出零点位置，并将其作为峰值，这一过程中是粗略的将最大点作为峰值。在实际应用中，由于采集到的散点图一般为多峰图，即存在多个零点微分值，且由于实际中可能出现的信号干扰会导致数据读取不完整。因此实际应用中，这种算法精度低。

1.2.2 高斯拟合。

反射光谱接近高斯函数图象[14]，因此可以将采集结果先进行高斯拟合，拟合为原始波形曲线。其中高斯函数的表达式为：

公式（7）中，a表示函数的幅值，b为常数，c表示函数的峰值位置的横坐标，δ表示函数的标准差即函数图形宽度。采样序列为采样点的个数为n，则误差函数为误差平方和为：

最后令误差和平方取最小值得xi值为峰值，即可得出其横坐标值。

1.2.3 多项式拟合

多项式拟合法是指在经过阈值限定后，利用最小二乘法原理对采集数据进行拟合，不断地迭代迫近，使得平方差和达到最小值，直至得到还原度最高的波形曲线[15]。光纤光栅的反射光谱可以根据这个方法拟合得到较高精度的函数曲线，进行峰值计算后即可得到最终结果。

多项式的表达式为：

光谱拟合函数为二次多项式可表示为：

设定采样点为：，则采集数据曲线和拟合曲线的误差平方和为：

同理，在进行微分得到最小值后，即可得出二次项式的系数，继而通过计算得到中心波长。

1.2.4 高斯-多项式拟合

髙斯拟合和多项式算法同时分析，形成一个新的寻峰算法高斯多项式拟合算法，FBG 的反射光谱曲线用高斯函数进行拟合后，则可以进行对数变换将其表达式改写为二次项形式，按照上文中多项式拟合的方法进行系数计算，再进行对数的反变换，就可以得到高精度拟合结果。

2 FPGA实现

光纤光栅解调的性能需求为：解调范围为1525 nm-1565 nm；解调速率为1 kHz；解调稳定性为正负1 pm。针对这种场景下精度、速度以及准确度要求比较高的需求，采用FPGA 进行控制处理和算法实现，可以在保证精度的前提下加快运行速度，采用的FPGA 芯片为Cyclone IV 系列的EP4CE10F17C8。

算法的流程设计框图如图2所示，数据输入之后对采样点进行阈值过滤后调用FPGA 内部的乘法器、加法器等实现高斯拟合算法，对输入曲线进行拟合，然后使用多项式进行拟合。

图2：寻峰算法运行流程图

FPGA 的运行需要使用Verilog 语言在Quartus II 13.1 平台上进行开发，FPGA 的运行是按相关模块运行的，包括了时序控制模块、AD 模块、数据缓存模块、运算处理模块以及通信模块。其中时序控制模块的作用是为各个模块提供适合的时钟信号，为简化设计，采用的方案是调用QuartusII上名为ALTPLL 的IP 核，通过分频和倍频等方式产生相应的时序信号。

采用的AD 采集芯片为AD9225，FPGA 给定AD9225芯片一个输入时钟后，在触发开始后接收到脉冲信号，将每个周期采集到的数据进行处理并存入到储存模块，然后合并转换为输出结果。其中输入的时钟设定为10 MHz，在FPGA 系统复位后经过8 个时钟延时后就可以读取到采集结果。

在经过AD 采集后的数据存入到数据缓存模块RAM 中，RAM 是QuartusII 上调用的IP 核，对这些缓存的数据进行接收后就可以将其输入到控制和运算模块中。

在接收到缓存数据后，需要对其进行运算处理，这个过程就是依据前文中的原理式，再调用所需的加法器乘法器等完成算法实现拟合。

3 算法实现和测试

3.1 算法拟合

在如图3所示的光谱图象中，可见多处极大值。因此需要设定如图4所示的相应阈值P1，将低于这一阈值的数据点筛除，而后只对达到阈值的数据点进行归纳和处理以节约运算资源。实验过程中，选取的阈值大小为最大过滤值的0.6倍即1.2V 最为合适，经过运算处理后得到如图所示的不同算法的拟合结果。

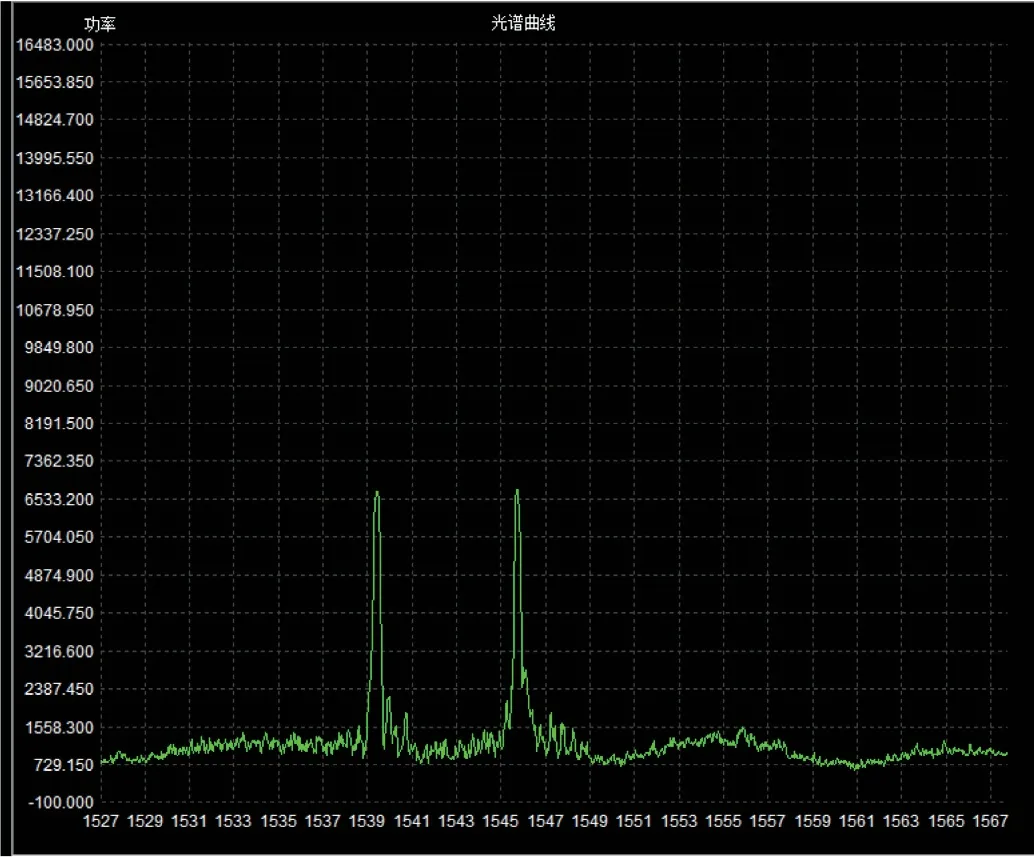
图3：光谱图象

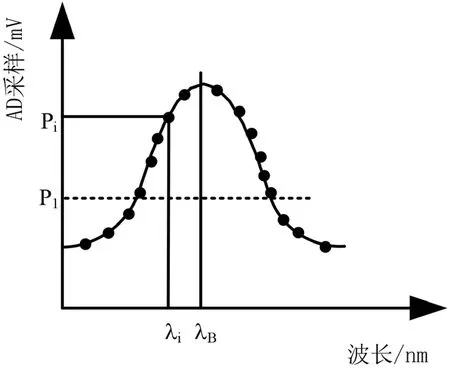
图4：采样阈值设定

在实验中，测定环境的温度为19.7℃，设定的激光器步进波长为25 pm，那么1525 nm-1565 nm 范围内扫描一次可以获得1500 个采样点，频率为1 kHz。FBG 传感器工作时，波长对温度和压力同时敏感，会出现多峰的现象，如图3 所示，采用的光纤光栅传感器的理论零点双中心波长为1540 nm 和1546 nm。

对于这种多个波峰的情况，解调时需要计算散点图中前后两次采样点的波长差，超过一定范围则认为出现新的波峰，波峰判断完成后，再对单一波峰拟合求峰值信息，提取图中1540 nm 附近的波形后，经过寻峰算法就可以完成第一个采样波峰拟合，如图5所示分别为直接法、高斯法、多项式法和高斯-多项式法的拟合结果，同理也可以得到第二个波峰拟合情况。

图5：波峰曲线拟合结果图

将各个算法拟合结果进行统计归纳后得到如表1所示的各个算法误差大小。

表1：寻峰算法的误差值

由表1 数据可知，直接比较法的误差较大，精度较低，在多次测试中误差均接近12 pm，高斯拟合法和多项式拟合法的误差值也不能达到设定要求，精度需要提高，而将高斯拟合和多项式拟合相结合的方法的精度有了明显提高，误差均低于0.5 pm，能够满足系统的解调需求。

3.2 温度变化拟合

将波峰数据的散点图进行波峰曲线拟合后，需要进行温度变化的感知实验。实验中将传感器所处的温度从20℃升温至70℃，而后从70℃降温20℃以完成升温和降温的温度变化测试，测试实验共做三轮，对三轮中得到的三组数据进行取平均值处理。而后对三组数据中温度对应的波长值取均值，可得到温度的变化数据值。

升温阶段的解调波长与温度响应曲线如图6所示。

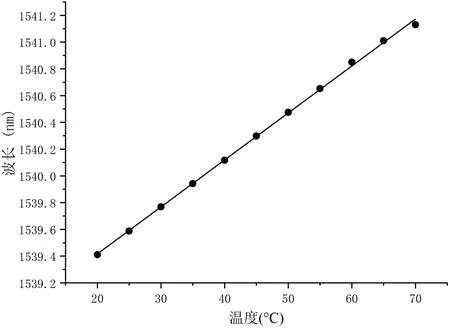
图6：升温标定图象

降温阶段波长和温度关系如图7所示。

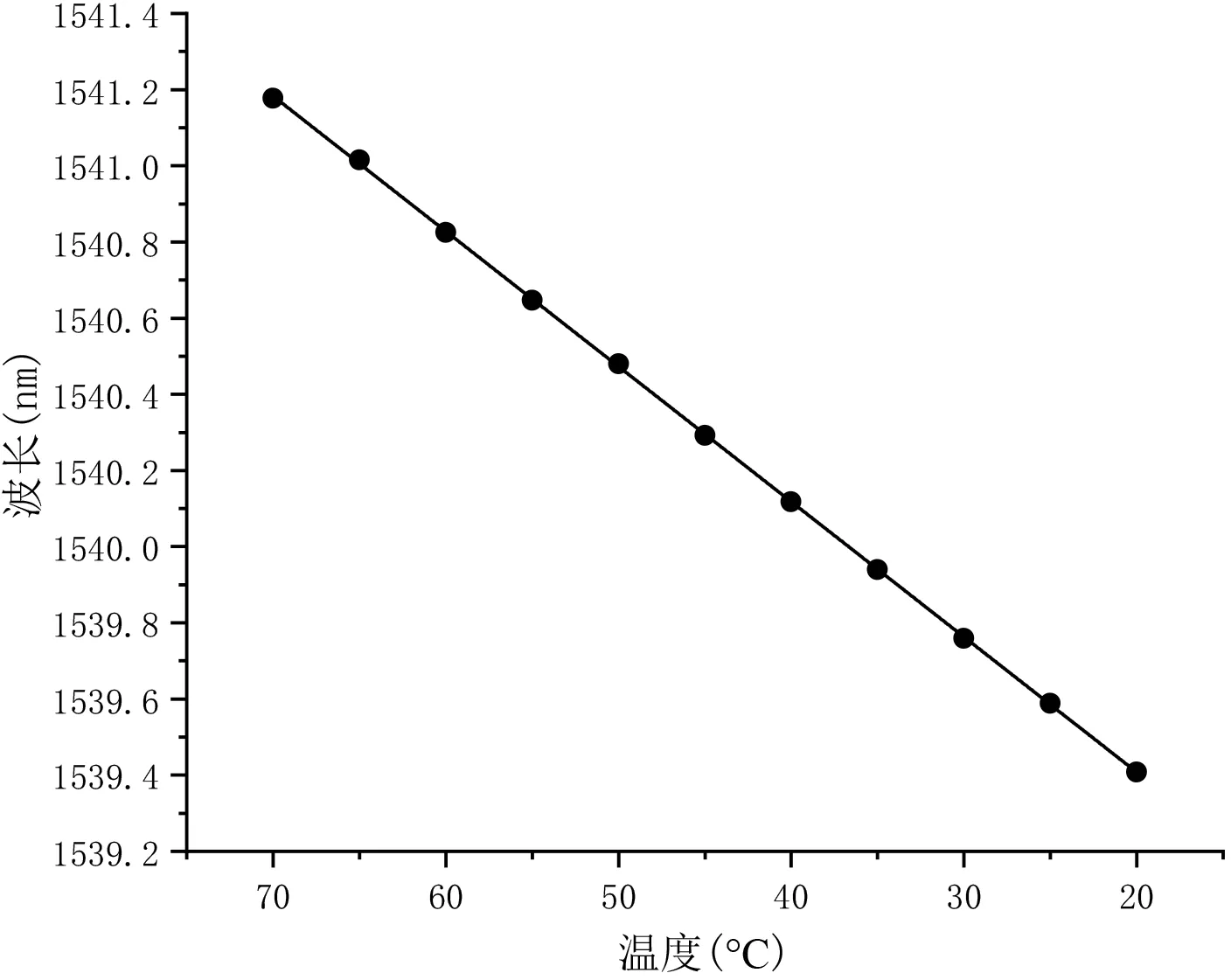
图7：降温标定图象

温度的波长标定结果显示，升温的标定结果为：

升温响应曲线的线性相关性为99.92%，升温的温度标定曲线拟合结果精度较高，表明系统的升温响应精度能够达到要求。降温的标定结果为：

降温响应曲线的线性相关性为99.94%，降温阶段的拟合精度与升温阶段一样较高，能够满足性能指标。

综合升温和降温的情况可知，温度的响应精度较高，且误差在1℃内，这一性能指标可以满足对水温的监测需求，同时可知，所设计的解调系统温度和波长标定误差较低具有极高的分辨率。

3.3 压力变化拟合

考虑温度对波长的影响为了减少测量误差，在进行压力拟合时需要相对应的温度光栅进行补偿。实验在19.7℃室温下进行，测试的范围在0 ～5MPa。压力的标定测试实验同样需要进行三组升压和降压测试后取平均值。

得到升压拟合数据如图8所示。

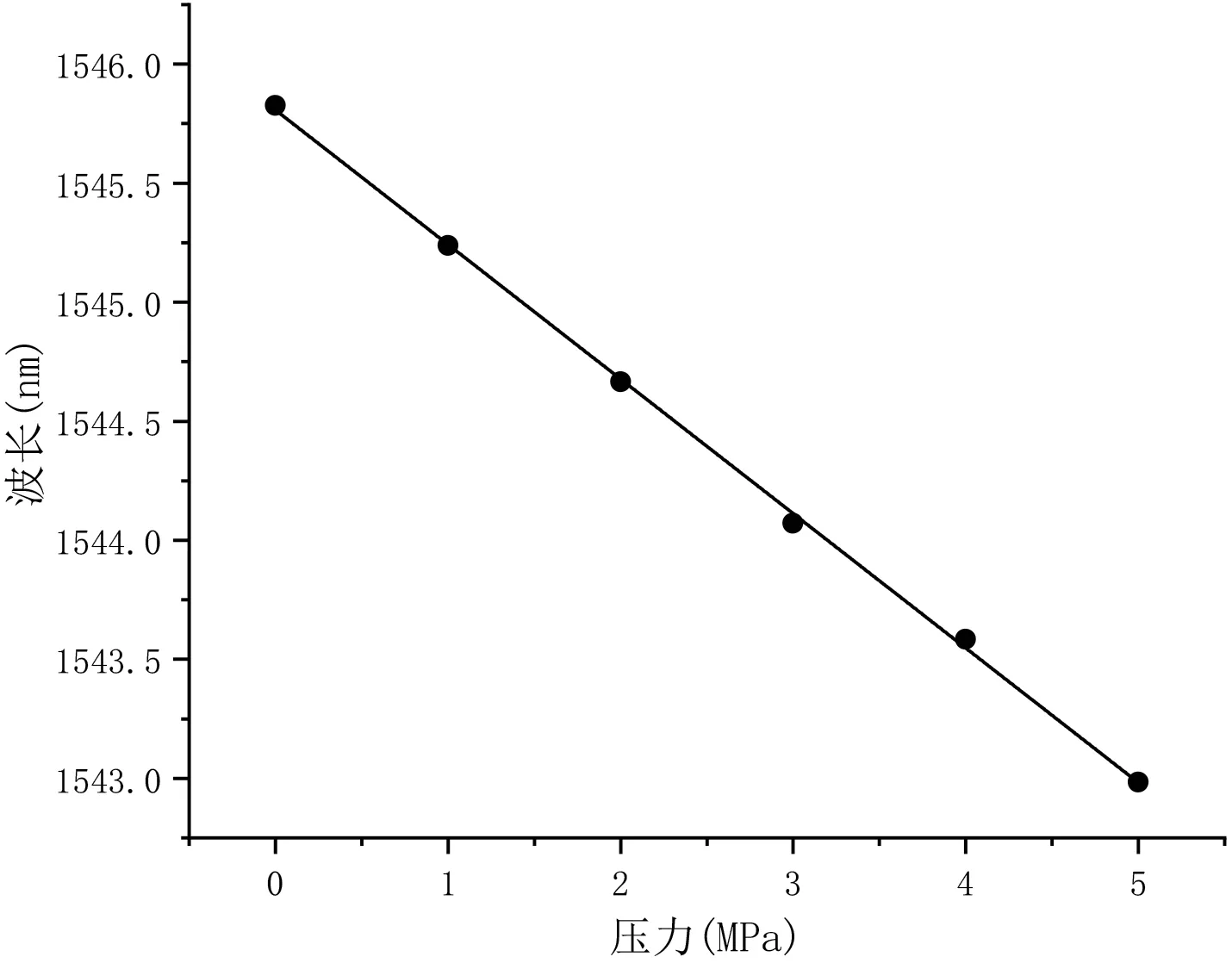
图8：升压标定图象

降压拟合情况如图9所示。

图9：降压标定图象

压力的波长标定的结果显示，升压阶段的标定结果为：

升压响应曲线的线性相关性为99.91%，升压的阶段的压力标定曲线拟合结果精度较高，表明系统的升压响应精度能够达到要求。降压的标定结果为：

降压响应拟合曲线的线性相关性为99.93%，降压阶段的压力标定同样能够满足性能需求。

综合升压和降压的情况可知，压力的响应精度较高，且误差在0.1Mpa 内，这一性能指标可以满足对水压的监测需求，可知所设计的解调系统压力和波长标定误差较低具有极高的分辨率。

4 结语

针对复杂环境下的温度和压力监测需求，设计了一种基于可调谐激光器的FBG 波长解调系统，完成了基于FPGA控制和运算程序设计，数据采集。在所需监测的温度和压力范围内，分别实现了它们对应波长的标定，使得系统能够实现高精度监测目标物理参量。

实验测试表明设计的高斯-多项式拟合算法在实际测试中具有最高的精度，多次测试中其误差值均低于0.5 pm，系统的解调频率达到1 kHz，温度标定的误差在1℃内，压力的误差在0.1 MPa 内。

设计的基于高斯-多项式拟合算法的FBG 解调系统，能针对光的波长进行高性能解调，实现复杂环境下针对的温度和压力等物理参量的高精度监测。