基于支持向量机的五轴数控机床加工精度预测方法

张书红

(合肥财经职业学院建筑工程学院,安徽 合肥 230601)

0 引言

五轴数控机床专精于复杂曲线零件的制造，运用于国家航空航天事业、军事、科研和医疗等各个领域，对这些领域的发展都有着重要的影响[1]。伴随社会生产需求的提高，对数控机床生产零件精度和效率的要求也在提高。随着数控机床的不断优化，科技含量和精密度越来越高，五轴数控机床成为了制造重型发电机转子和叶轮等加工工业的首要选择。现阶段，很多国内的加工工业都选用五轴数控机床进行加工，它的加工效率是三轴数控机床的2～3倍，可以有效节约生产投资成本和生产空间。但我国的五轴数控机床还处于发展阶段，在稳定性和精准性方面还存在一定的问题，因此需要对五轴数控机床加工精度进行预测。基于此，有学者提出基于搭建的机床机械系统和控制系统模型，通过Adams/Control模块对接Simulink建立的控制模型，进而计算出误差值，从而实现五轴数控机床加工精度检测。该方法具有一定的有效性，但对加工零件的预测有局限性，其预测效果较差[2]。

基于上述问题，本文研究基于支持向量机的五轴数控机床加工精度预测方法。支持向量机是一种以统计学理论和结构理论为基础的方法，能够在一定样本中识别到样本的信息，并具有一定的学习能力，将识别到的样本能力进行推广，进而得到推广效果。支持向量机能够有效识别出样本中特有的优势和特点，并且对小样本、非线性及高维模式的识别效果最好，它可以把识别到的优点运用到机器学习问题里，提高机器学习的效率。当机器学习时，支持向量机起到监督学习的作用，可以基于支持向量机构建一个监督学习模型。通过分析五轴数控机床特性，提取五轴数控机床特征，通过支持向量机构建加工精度预测模型，预测五轴数控机床存在的影响精度因素，结合粒子群优化算法完成机床加工精度的预测。

1 基于支持向量机的五轴数控机床加工精度预测方法

1.1 提取五轴数控机床特征

为了构建加工精度预测模型，需要掌握机床工作的原理，了解五轴数控机床的生产过程，提取五轴数控机床特征。五轴数控机床运用的领域较广，加工生产产品的特点和特性要求不一，因而在生产零件时，需要对五轴数控机床进行相应的调试和检测。选取一台双转台类型的五轴数控机床，分析它的内部结构。双转台类型的五轴数控机床比三轴数控机床多了2个摆头和2个转台，在加工时，摆头部件和转台部件交叉使用。五轴数控机床的具体结构和参数指标如表1所列。

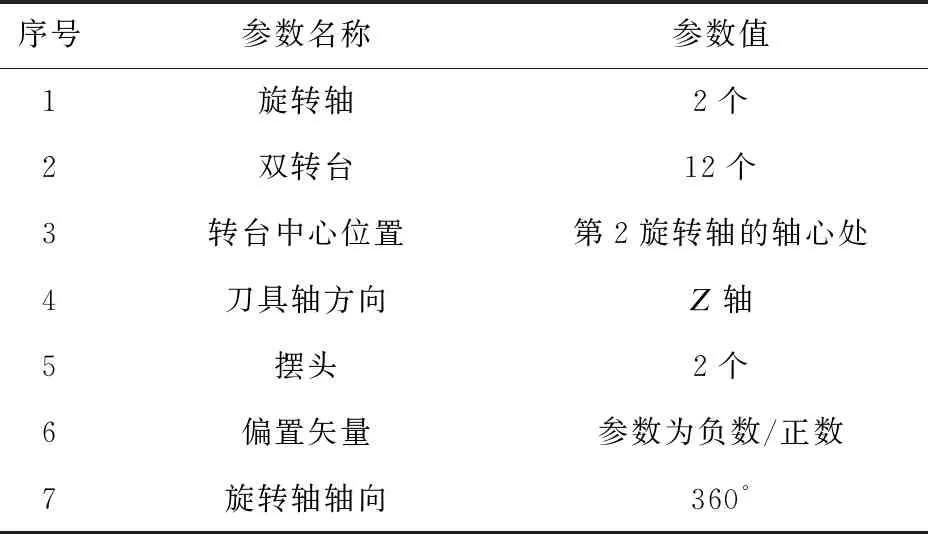
表1 五轴数控机床参数表

由于五轴数控机床的结构不同，偏置矢量会因为结构的不同而产生变化，参数可能为负数，也可能为正数。五轴数控的结构具有一定的灵活性，可以将转台和摆头的轴结构分别设置为a轴、b轴和c轴，内部部件可以根据加工需求进行组合，每个旋转轴相互配合[3]。在研究基于支持向量机的五轴数控机床加工精度预测方法时，首先要掌握五轴数控机床指标参数和结构特点。机床结构和指标参数是影响加工精度的主要因素。数控机床加工精度是保证产品质量的前提条件，准确找出加工精度的误差来源，可确保产品的尺寸大小和厚度符合生产标准。通过预测五轴数控机床加工精度方法，能够有效保障机床加工的性能，及时判断出数控机床存在的问题，当数控机床加工零件时，一旦出现误差可以及时调整[4]。预测方法就是在加工之前进行判断和调试。预测方法可以预测数控机床的稳定性、加工数量和误差来源等多个方面，可以提前制定相应的解决措施。五轴数控机床每个部件都具有一定的特性，在提取机床特征的基础上，要掌握每个部件的特性，机床运行时，部件会发生一定变化，部件产生的变化会影响五轴数控机床的加工精度。

1.2 基于支持向量机构建加工精度预测模型

为了有效提高五轴数控机床加工精度预测效果，需要通过支持向量机构建加工精度预测模型，同时，预测五轴数控机床存在的影响精度的因素。因此，需要分析五轴数控机床的多个部件组成(机床床身、工作台和溜板等)在进行加工时，部件和部件之间的关系[5]。五轴数控机床在进行加工时，每个部件之间都在相互配合运行，部件之间产生的摩擦在一定程度上会影响加工精度。五轴数控机床加工的产品尺寸一般较小，对产品的精度有较高的要求，在加工之前提前预测数控机床精度尤为重要。把数控机床的部件看成是1个单独的整体，预测部件存在的精度误差值，掌握部件之间运行时产生的精度误差值，在此基础上，构建加工精度预测模型。把五轴数控机床看成1个几何体，它的几何特点表现得非常明显，通过几何特点的特性可以将数控机床加工精度预测问题看成几何问题。建立1个三维坐标，分别设置有A、B、C3个方向，将五轴数控机床代入到三维坐标中，机床的某一点沿着A方向移动时会产生定位误差值，当沿着B和C方向移动时，则会产生直线误差值[6]。五轴数控机床在三维坐标系中滚动时，向每个方向滚动的误差也有所差异。构建的精度模型主要用来分析三维坐标系中不同方向的误差值。根据五轴数控机床内部特征和结构特点，构建一个三维坐标系，坐标系结构如式(1)所示。

L=AiBiCii=0,1,2,3，…,n

(1)

式中：A、B和C分别表示三维坐标系的3个不同的空间方向。

通过五轴数控机床三维坐标设定机床加工刀具的坐标结构，如式(2)所示。

Q=[R,T,Y]

(2)

式中：Q表示刀具坐标；R表示在A轴上的数值；T表示在B轴上的数值；Y表示在C轴上的数值。

由于五轴数控机床在移动时，各个部件也会发生移动，计算出每个部件的坐标值，将坐标体系结构转化为函数问题，每个部件的坐标数值直接关系到五轴数控机床加工精准程度[7]。五轴数控机床中的刀具是切割工具，是控制数控机床精度的重要条件，所以刀具坐标点的移动情况关系到精度模型预测的效果。机床内部有多个刀具，刀具之间的距离也可能是误差来源。首先需要判断产品切割时，刀具的具体位置根据标准位置进行设定，利用精度模型，分析刀具坐标点是否在标准范围内，控制好刀具带来的误差值。刀具是切割产品的重要工具，不同产品加工时，需要的刀具不一样，甚至需要五轴数控机床中的刀具进行组合排列完成，刀具之间的配合度以及刀具之间的距离都能影响加工精度。基于支持向量机构建的精度模型能够准确计算出五轴数控机床的几何误差、系统运行误差以及加工过程中产生的热误差。由于这几种误差引起的原因各不相同，预测难度也不一样，其中最容易预测的是几何误差。精度模型会将这些误差进行汇总，对五轴数控机床进行总体判断。

1.3 粒子群优化算法预测机床加工精度

由上述可知，影响五轴数控机床加工精度的因素较多，需要对这些影响因素进行优化，才能够有效保证数控机床运行轨迹、运行速度和制造精度，调整数控机床的结构参数。以支持向量机为创新点，构建的精度模型能够有效计算出机床结构中的几何误差，但机床误差还包括伺服系统误差，这就需要利用粒子群优化算法计算系统误差，及时调整系统参数。五轴数控机床的操作指令主要是由计算机中的软件系统发出的，根据系统指令完成一系列的加工任务[8]。利用粒子群优化算法能够从系统的软件方面入手，控制软件指标参数，控制好五轴数控机床加工位置。本文提出的粒子群优化算法能够整体提高数控机床的性能，从全局的角度出发，优化全局。将五轴数控机床分成几个区域，通过粒子群算法，计算出各个区域的最优解，把每个区域的最优解进行融合得到全局的最优解。粒子进行迭代计算，在达到最优解的过程中，不断调整系统参数，控制好数控机床切割位置，使位置确定在标准范围之内。通常把粒子的维度作为优化参数的个数，有多少个维度就有多少个需要优化的参数。优化维度也就是优化粒子，系统中的每一个粒子都有一个最优的位置，需要找出每一个粒子的最优位置[9]。粒子速度也是影响加工精度的重要因素，因为五轴数控机床中的各部件相互配合，速度快慢能够影响部件的配合程度，也需要通过粒子算法找到最优的粒子速度。根据粒子群优化算法，不断地进行更新，更新的信息可以用式(3)表示。

F=G+H

(3)

式中：F表示粒子维向量；G表示最优位置；H表示最优速度。五轴数控机床的速度和位置作为优化的主要对象，通过寻求速度和位置的最优解组合，从而有效地找到所有粒子的最优解。粒子群优化算法计算最优解的过程一共分为3个步骤。第1步：确定好粒子个数，维度和随机赋值；第2步：对粒子群进行综合评价，寻找一个最优的优化方向，得到一个优化标准值的范围；第3步：让每一个粒子达到这个标准值，不断优化它的位置和速度，最终观察这些误差值，是否满足加工条件。具体粒子群优化算法流程如图1所示。

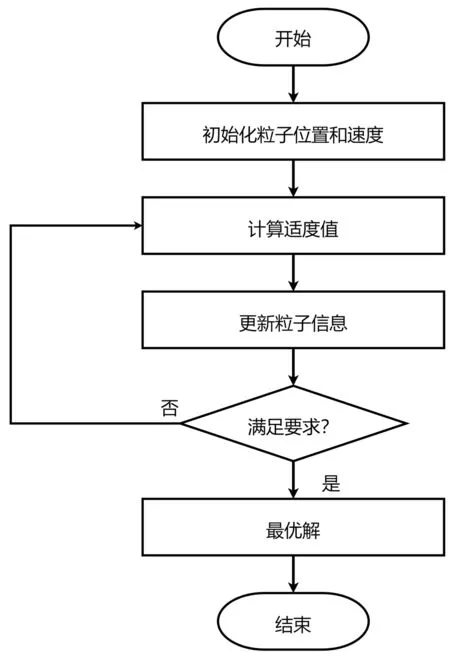
图1 粒子群优化算法流程图

在这个过程中，粒子速度和位置的更新是这个流程的核心部分，运行中需要不断更新粒子信息，调整粒子位置范围和速度的快慢，最终使这个粒子位置和速度达到一个标准值。根据上述对粒子的调整，采用粒子群优化算法，能够有效判断出五轴数控机床每个粒子的位置和速度是否满足标准要求，如果不满足，则预测方法能够及时判断出粒子没有达到最优解，计算出全局最优解，找出解决问题的办法，提高预测的精准性和及时性。综合上述分析，实现五轴数控机床加工精度预测。

2 实验与分析

2.1 实验准备

为了检验基于支持向量机的五轴数控机床加工精度预测方法，开展测试实验。首先选取一台某生产厂家的五轴数控机床，假设五轴数控机床的结构和工作系统误差值和误差个数均为0，一共选取15个测量区域，分别用D1、D2、D3、D4、D5、D6、D7、D8、D9、D10、D11、D12、D13、D14、D15表示这15个测量区域，对这15个测量区域进行误差值和误差个数调试，15个测量点调试的实际误差值如表2所列。

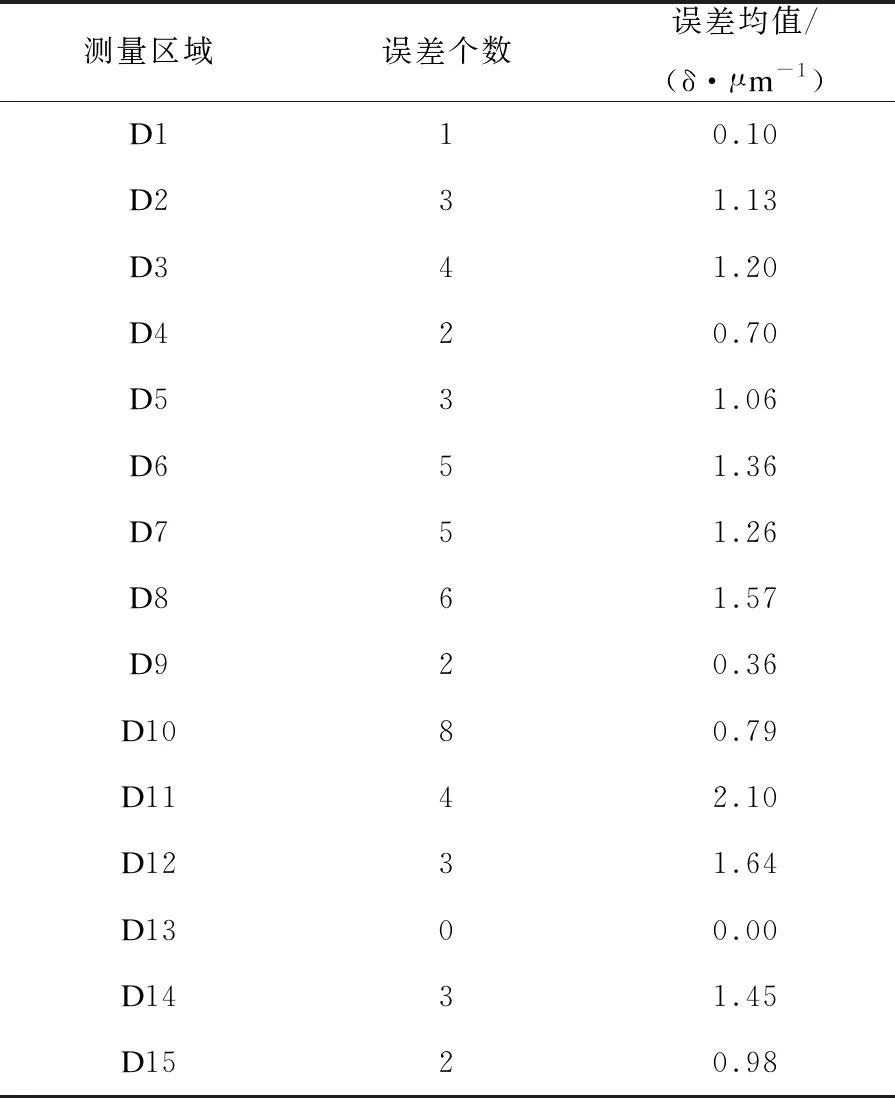
表2 实际测量区域误差值

根据表2可知，这15个局部区域为预测的对象，将区域中的误差值作为变量，在此基础上，需要设置实验设备参数，确保实验环境的稳定性，分析基于支持向量机的五轴数控机床加工精度预测方法是否能够有效计算出这15个区域的误差值。设置整个实验环境和实验对象，分别采用基于支持向量机提出的五轴数控机床加工精度预测方法(简称当前方法)和当前加工精度预测方法(简称本文方法)进行预测，通过这两种方法测量出区域的误差值，分析这两种预测方法的效果。

2.2 实验结果

对误差值进行预测，其数值为式(4)所示计算结果,

(4)

式中：λ1和λ2分别为系统显示机床运行部件位置与实际机床运行部件位置的差值；η1和η2分别是部件与部件之间产生的误差系数和部件与产品之间产生的误差系数。

根据上述实验准备开展实验，通过公式获取本文方法的误差值，将本文方法和当前方法的误差值进行对比，对比结果如表3所列。

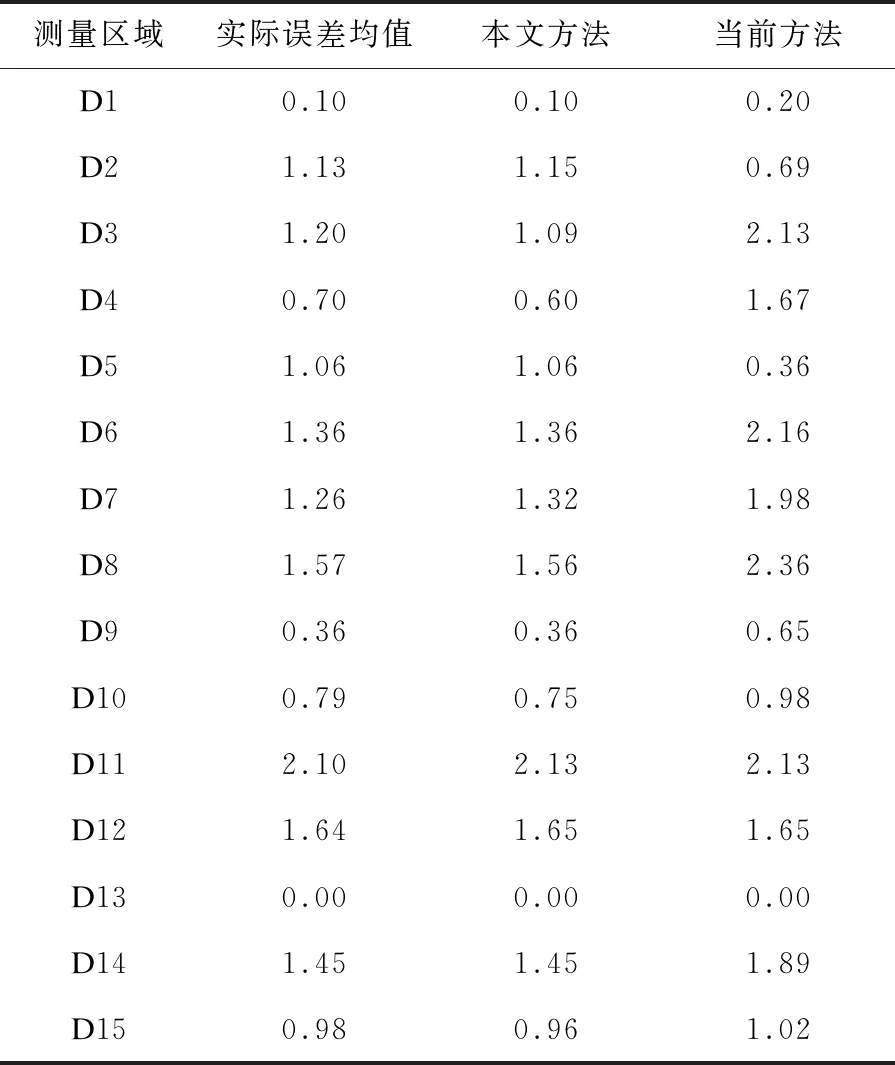
表3 两种方法预测结果 (δ/μm)

根据表3可知，15个区域的实际平均误差值为1.05 δ/μm，所提方法预测平均误差值为1.03 δ/μm，当前方法预测平均误差值为1.33 δ/μm，所提方法预测的误差值与实际误差值只相差了0.02 δ/μm，而当前方法预测的误差值与实际误差值相差了0.28 δ/μm。由此可知，当前方法预测数控机床的误差值偏大。用基于支持向量机的五轴数控机床加工精度预测方法进行预测时，预测出来的误差值与实际误差值偏差较小，具有一致性，其中在D1、D5、D6、D9、D13、D14区域中，预测的误差值与实际误差值相同。采用当前预测方法进行预测时，发现预测的误差值与实际误差值有很大的偏差，并且只有在区域D3中预测的误差值与实际误差值相同，预测其他区域的误差值都有一定的偏差。实验结果说明了本加工精度预测方法能够有效测出五轴数控机床的内部结构的误差值，预测精准性较高，本文方法的预测效果更好。因为本文方法在掌握每个部件特性的基础上，对机床进行特征提取，提高了部件特征值的精度。通过支持向量机构建加工精度预测模型，能够有效分析出每个测量区域的误差参数个数。利用粒子群优化算法，获取最优的粒子速度，计算出每个误差参数的误差值，从而减小了预测误差值，提高了预测精度。

3 结语

文章研究了基于支持向量机的五轴数控机床加工精度预测方法，利用数控机床加工时，需要对机床的各个参数进行检查和调整，降低数控机床加工精度误差值，让加工出来的成品符合生产的标准。基于支持向量机构建的加工精度预测模型能够有效保障加工产品的精准性，及时调整机床结构参数，促进了加工事业的发展。由于影响五轴数控机床精度的因素较多，误差来源不同，需要从多个因素去分析，进行综合考虑。该研究只考虑了几种影响因素，没有从整体出发，希望在下一次研究中，能对五轴数控机床进行综合分析，利用综合评价理论对它进行多方面评价，建立一个更加稳定的模型。