基于Ramp-VG阵列的超声速混合层流动控制实验研究

夏梓豪, 丁浩林, 易仕和， 孙明波

(国防科技大学空天科学学院, 湖南长沙 410073)

引言

当红外成像制导导弹在大气层中以高速(通常指Ma>3)飞行时, 通常需要利用冷却气膜隔离外部高温主流对红外光学窗口的加热, 以避免飞行器光学窗口承受严重热负荷, 造成窗口过热淹没目标红外信号, 甚至造成成像窗口损坏[1-3]. 但是冷却气膜和光学窗口外部主流相互作用, 可能会形成包含边界层、 激波、 混合层及其相互干扰形成的复杂流动结构, 如图1所示, 对目标信号传输产生影响, 引起光线出现偏移、 抖动、 扩散以及能量消减, 这种现象一般统称为气动光学效应[4-6]. 在光学窗口附近的复杂流动中, 混合层导致的光线抖动、 扩散和能量消减最为显著, 占比可达90%[7]. 那么, 如何抑制混合层导致的气动光学效应就成为消减光学窗口气动光学效应的重中之重.

图1 带冷却气膜超声速光学窗口流动显示测量结果[5]

目前国际上常用的流动控制技术主要分为两类: 主动控制和被动控制[8]. 相比于主动控制, 被动控制具有结构简单、 加工容易、 成本低廉和不需要额外能量输入等优势, 对于减小和优化飞行器质量和构型具有重要意义, 在工程实现上难度相对较小, 目前应用比较广泛[9-11]. 与此同时, 被动控制装置(狭义上指涡流发生器)有多种构型. 1960年, Schubauer等[12]研究了不可压流动中“混合增强装置”(包括犁型、 鱼鳍型、 槽型、 斜坡型等构型)对边界层内逆压梯度区的作用和影响, 发现混合增强装置的作用效果不一, 但都能够降低逆压梯度区的压力梯度. 1990年, Lin等[13]用油膜法研究了低速情况下多种被动控制技术对曲面后台阶流动的控制效果, 发现斜坡型、 人字型、 拱型等构型的涡流发生器可以减小后台阶后的流动分离, 引起一部分压力恢复. 2006年, Anderson等[14]在NASA/GRC 15 cm×15 cm超声速风洞中研究了3种构型的微型涡流发生器阵列对激波/边界层干扰(shock boundary layer interaction, SBLI)的控制作用, 发现微型ramp阵列的控制效果最好, 与边界层抽吸的效果相似, 并且得到了ramp的最优设计. 此后, Blinde等[15]和Ford等[16]利用Anderson的结果对SBLI问题进行了深入研究, Ramp-VG由此开始成为研究热点. 不过, 关于RVGA对超声速混合层具有怎样的控制作用, 国际上还没有相关的研究.

本文利用NPLS技术, 获取了有/无Ramp-VG控制下超声速混合层的流动显示结果, 分析其流动控制机理, 进而为该技术应用于带气膜冷却光学窗口气动光学效应抑制提供理论支撑.

1 Ramp-VG

早在1960年, Schubauer等[12]就提出了Ramp-VG, 只不过那时Ramp-VG被归类为“混合增强装置”, 2006年Anderson等[14]利用Response Surface Methodology(RSM)方法计算得到SBLI流动控制问题中Ramp-VG的最优设计参数以后， Ramp-VG才开始作为一种独立的涡流发生器出现并被广泛用于流动控制, 见图2.

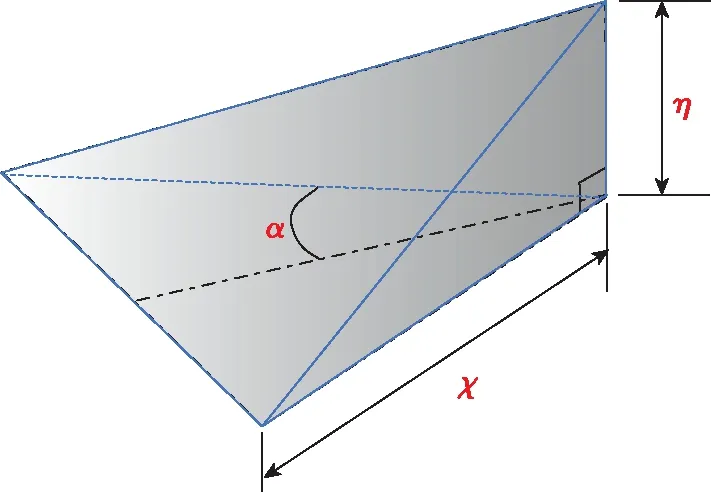
图2 Anderson Ramp-VG几何构型[14]

Anderson Ramp-VG是一个三角形前台阶, 独立设计参数有3个, 分别是高度h、 弦长c和入射角α.结构简单、 变量明确是Anderson Ramp-VG的优点之一, 研究者可以据此研究各个参数对其性能的影响, 针对一类问题, 容易得到系统的、 全面的Ramp-VG设计参数. 此外, 相比于其他构型的涡流发生器, Ramp-VG更加结实坚固, 不易损坏, 实验时更加安全, 也更容易运用到工程实际当中.

Babinsky等[17]通过油膜法研究, 详细描述了Ramp-VG周围的流场结构, 如图3所示. 这对于解释和分析单列Ramp-VG阵列的流动现象和流动机理有巨大的帮助. 首先, 来流与Ramp-VG相遇并在其前缘产生微小的分离区, 随后, 这个分离区产生一个非常细小的马蹄涡. 尾流区的主要特征是由一对反向旋转的1阶涡构成的人字形涡结构. 在Ramp-VG和壁面连接处, 1阶涡引起的流动分离产生了一个2阶小涡. 在Ramp-VG后缘有一个小的流动分离区, 也会产生一个2阶小涡.

图3 单个Ramp-VG周围的流场示意图[17]

将多个Ramp-VG按照一定的形式组合起来便可以得到涡流发生器阵列, 其独立设计参数有两个, 分别是安装间距s和安装位置Xp, 如图4所示. 其优点是能够在更宽广的空间范围内得到规律性的尾流区, 这也是实际工程应用中的布置方式, 因为不可能只用1个或2个Ramp-VG来综合改变尾流状态.

图4 Ramp-VG阵列示意图

Ramp-VG阵列可以有多种形式. 可以是单列也可以是双列甚至多列, 多列时可以交错排列也可以前后对齐. Schubauer等[12]通过研究指出, 不可压情况下s和Xp取适当值时, 单列涡流发生器改善流动分离的效果比多列要好. Schreyer等[9]实验研究了一种两列涡流发生器阵列对SBLI的影响, 发现其极大改变了流场结构, 使得原本的二维干扰区发展成三维干扰区.

目前关于单列涡流发生器阵列的研究较多, 因为人们对单个Ramp-VG的作用机理研究较为透彻, 单列Ramp-VG阵列变量少、 容易控制、 便于研究. 多列Ramp-VG阵列形式多样、 控制机理尚不明确, 目前还没有太多的相关研究. 本文的研究问题比较新颖, 因此采用单列Ramp-VG阵列进行研究.

2 实验设备

2.1 超声速混合层风洞

本文实验均在国防科技大学超声速混合层风洞中进行, 该风洞是一座吸气式直连超声速风洞, 风洞实验段尺寸为100 mm×120 mm. 稳定段低速侧(上侧)安装有调压阀和整流器, 可以连续调节低速侧的压力, 得到压力匹配混合层流场， 见图5.

图5 国防科技大学超声速混合层风洞示意图

实验总温T0=303 K, 来流Ma1=3.6(下喷管)、Ma2=2.6(上喷管). 高速侧总压P01=101.0 kPa, 低速侧静压P2由喷管前缘的壁面静压孔测得, 由于稳定段内部气流速度较低, 则低速侧总压P02≈P2=19.2 kPa. 空气湿度75%. 喷管段中间隔板后缘的边界层名义厚度δ99≈1 mm.

根据等熵关系式、 声速定义式和对流Mach数定义式可以计算出喷管出口的流场参数

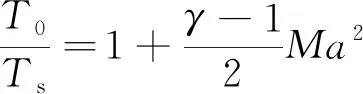
式中,Ts为静温,T0为总温,γ为比热比(γ=1.4),R为气体常数(R=287 J·kg-1·K-1),Ma为喷管Mach数,a为声速,Mac为对流Mach数. 计算后得到的超声速混合层流场参数如表1所示.

表1 超声速混合层流场参数

2.2 RVGA

实验所用的RVGA为单列构型, 其参数均为自主设计, 其几何参数如图6所示,a为Ramp-VG尖端的宽度,d为Ramp-VG凹槽的宽度,D为相邻两个Ramp-VG尖端的间距,h为Ramp-VG尖端的高度,L为Ramp-VG底部斜边的长度, 2α为Ramp-VG底部两斜边的夹角.

图6 RVGA示意图

相比于常规Ramp-VG, 可以看到模型的后缘被削平, 使得模型总体上呈梯形(这一构型最早由Verma等[11]提出, 用于研究对激波边界层干扰的控制作用), 这是为了便于加工, 因为模型的高度仅为1 mm(h～δ99); 同时, 模型中Ramp-VG数量较多, 间距D较小, 所有的Ramp-VG连为一体, 以便于模型安装和减小安装误差.

2.3 NPLS技术

NPLS技术是一种新型流动显示技术, 其核心是采用纳米粒子作为示踪粒子, 具有高时空分辨率和高信噪比. 图7为NPLS系统示意图[18], 系统由计算机、 同步控制器、 CCD相机、 脉冲激光光源、 纳米粒子发生器、 光臂和片光镜头组成.

图7 NPLS系统示意图[19]

纳米粒子发生器能够为流场提供均匀连续的纳米示踪粒子; 同步控制器用于控制相机、 激光器、 纳米粒子发生器和图像采集卡的工作时序, 其时间精度为0.25 ns; 激光光源为双腔 Nd∶YAG 激光器, 输出波长532 nm, 脉冲持续时间6 ns, 单脉冲最高能量为350 mJ; 本实验中采用的CCD相机的分辨率为2 000×2 000, 每个像素的灰度等级为4 096; 光臂用于激光束的传输; 片光镜头则用于将准直激光束转换为实验所需的片光光源, 实验中所用片光镜头焦距为50 mm, 束腰厚度约为1 mm. 已有大量实验结果表明, NPLS技术能够很好地再现超声速流场中的激波、 膨胀波、 滑移线、 湍流边界层和混合层等精细流动结构, 完全满足本文实验中对超声速混合层流场结构拍摄的需求.

3 实验结果与分析

实验中坐标系定义如下: 以喷管段中间隔板后缘为原点, 平行于隔板向出口方向为X轴正方向, 垂直于隔板向上为Z轴正方向,Y轴方向按右手定则确定. RVGA与Y轴平行, 安装在中间隔板上侧X=-10 mm处, 见图8.

图8 实验条件及坐标系定义

实验均在混合层压力平衡条件下进行. 不加Ramp-VG阵列, 在连续微调调压阀的同时观察混合层纹影图像, 直到混合层层流段呈水平, 则认为混合层压力达到平衡, 如图9所示. 图像尺寸为190 mm×38 mm.

图9 混合层时间平均纹影图像

3.1 无控状态下超声速混合层的流场结构

图10是无控状态下拍摄到的两幅超声速混合层流向NPLS图像, 尺寸均为195 mm×32 mm, 拍摄间隔5 μs, 图像空间分辨率为0.106 mm/pixel, 图像左侧距离原点3 mm, 层流段长度33.6 mm. 选取图中特征最明显的流动结构作为特征结构A, 通过测量发现A的移动距离为ΔS1=2.63 mm, 从而计算出A的运动速度为526 m/s. 超声速混合层具有快运动、 慢变化的特征, 故在5 μs时间间隔内, 大尺度涡结构的变形不明显, 只是整体上向下游移动了一段距离. 在图中可以观察到非常清晰的K-H不稳定涡, 如虚线框内所示, 其平均波长为λ=12.7 mm.随后, K-H 不稳定涡继续向下游移动并逐渐破碎, 混合层厚度不断增加, 最终发展成完全的湍流.

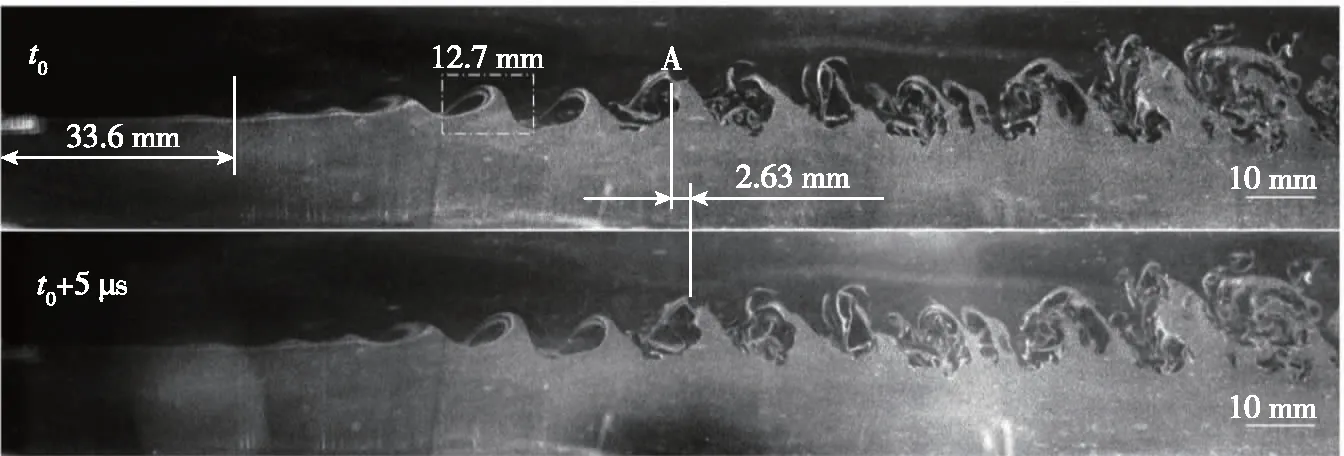
图10 无控状态下的超声速混合层NPLS图像

需要指出的是, 由于原始图像较暗, 无法辨识出混合层, 因此对图像做了亮度和对比度的调整. 经过处理后的图像左侧存在暗区, 说明在实验中激光片光打得不够均匀; 另外, 图像中存在一些大颗粒和玻璃划痕. 这些问题并不影响对于超声速混合层流动现象和流场结构的分析, 特此说明.

3.2 RVGA对超声速混合层的流动控制效果

图11， 12是加入RVGA控制的超声速混合层流向NPLS图像. 图像尺寸、 空间分辨率和拍摄间隔均与图10相同.

图11是y0位置的流动控制结果. 从图中测得K-H不稳定涡的平均波长为λ=9.1 mm, 层流段长度34.5 mm. 选取图中特征最明显的流动结构作为特征结构B, 通过测量发现B的移动距离为ΔS2=2.77 mm, 从而计算出B的运动速度为554 m/s. 与无控状态下超声速混合层的流场结构相比, 加入RVGA后y0处混合层层流段长度增加了2.7%, 并且混合层中的涡结构在形态、 尺寸和运动速度上都出现了明显的变化. 首先, 涡流发生器的控制作用使得涡的运动速度提高了5.3%; 其次, K-H不稳定涡提前破碎, 涡结构的尺寸明显变小(其中K-H不稳定涡的平均波长减小了28.3%), 混合层的各向同性增加; 第三, 混合层厚度明显降低. 根据Babinsky的理论可以做如下解释:y0两侧的Ramp-VG边缘产生了一对向下的反向旋转涡, 将上侧喷管内自由流中的高动量流体卷入喷管隔板边界层(后文简称为边界层), 与其中的低动量流体掺混, 提高了边界层的平均能量, 进而导致隔板后缘形成的超声速混合层的平均能量升高, 最终导致涡结构运动加快. 同时, 边界层能量的升高使得混合层的前期发展更加稳定, 但也使混合层转捩开始时涡的破碎提前. 并且, 这种动量下卷效应压缩了涡流发生器的尾流边界层的厚度, 相当于增加了低速侧的压强, 从而使得混合层厚度明显减小.

图11 施加控制时y0处的超声速混合层NPLS图像

图12是y1/2位置的流动控制结果. 从图中测得K-H不稳定涡的平均波长为λ=12.1 mm, 层流段长度37.9 mm. 选取图中特征最明显的流动结构作为特征结构C, 通过测量发现C的移动距离为ΔS3=2.99 mm, 从而计算出C的运动速度为 598 m/s. 与无控状态下超声速混合层的流场结构相比, 加入RVGA后y1/2处混合层的层流段长度增加了12.8%, 涡的运动速度提高了13.7%. 同样,y1/2处的K-H不稳定涡提前破碎, 涡结构的尺寸有所减小(其中K-H不稳定涡的平均波长减小了4.7%), 混合层的各向同性增加, 混合层厚度明显增加. 其成因分析如下: 首先,y1/2处的Ramp-VG前缘使边界层中的低动量流体抬升, 与自由流中的高动量流体充分掺混, 使边界层能量升高; 然后, 经过掺混的流体流过Ramp-VG后缘(相当于一个90°角的后台阶)后再附到隔板表面, 成为新的边界层; 最后, 尾流中存在一对向上的反向旋转涡, 使得边界层内的流体存在加速向上脱离壁面的趋势, 进而使得混合层上卷, 导致混合层厚度明显增加. 与y0处相比, y1/2处边界层与自由流的动量掺混效率更高, 隔板边界层的能量得到改善, 使得混合层的层流段长度得到进一步延伸, 涡的运动速度更大, K-H不稳定涡的破碎也更加提前. 并且, 这种动量上卷效应提高了涡流发生器尾流边界层的厚度.

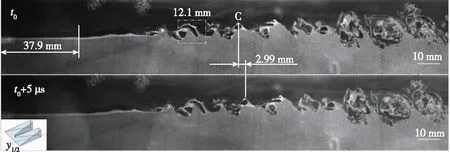
图12 施加控制时y1/2处的超声速混合层NPLS图像

可以看出, 提高上侧喷管隔板边界层的能量能够在一定程度上改善混合层的流场, 达到增强或减弱掺混、 减小涡结构各向异性、 提高流动速度和推迟转捩等目的.

3.3 分形分析

分形理论与湍流结合的可行性已经被许多研究验证[19-21], 通过计算分形维数(fractal dimension)来揭示湍流图像的内部规律. 超声速混合层中同时存在着层流和湍流, 以及大尺度涡结构和小尺度涡结构, 不具有特征长度; 且其整体和局部特征具有自相似性, 是分形理论研究的典型对象之一.

分形维数的计算方法包括“脚规”法、 “香肠”法和“数盒子”法等. 其中, “数盒子”法具有数字化处理过程方便, 网格尺度容易改变等优点, 是处理湍流的常用方法之一[22], 其计算公式为[23]

式中,Si表示第i个待分形区域,Nε(Si)是Si中含有湍流边缘的正方形网格(像素)数目,ε是网格的宽度.

图13是用Canny边缘检测算子捕捉到的超声速混合层界面, 为了研究流动的流向演化过程, 从x=18 mm开始将图像均分为12段, 每段长为15 mm, 逐一计算各段的分形维数, 计算结果如图14所示.

(a) Without control

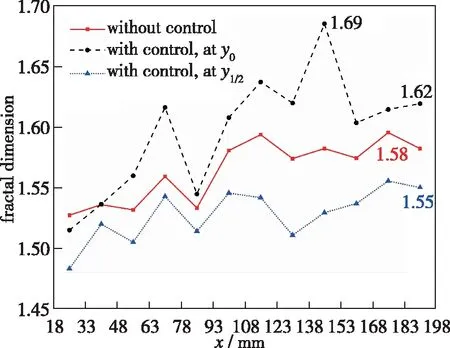
图14 沿流向分形维数分布

首先, 可以看出, 在任一情况下, 分形维数d都是在起伏中上升, 并最终稳定在一个值ds附近.无控状态时ds=1.58, 加入RVGA控制后y0处ds=1.62,y1/2处ds=1.55.折线图的变化趋势与NPLS图像显示的混合层发展过程相一致, 混合层前段是受速度剪切支配的, 为层流状态, 故分形维数较低, 随着混合层向下游运动, 展向涡的配对与合并导致混合层失稳, 混合层厚度增加, 大涡破碎为小涡, 混合层逐渐发展为湍流状态, 流动的分形维数保持在1.6左右.

其次, 引入控制后混合层的分形维数增长幅值大大改变.y0处的分形维数幅值增加,y1/2处的分形维数幅值减小. 这个变化说明, RVGA的控制作用改变了y0处和y1/2处的超声速混合层的湍流发展状态,y0处的湍流发展得到了加强,y1/2处的则得到了减弱.

4 结论

本文初次研究了RVGA(单列)对超声速混合层的流动控制作用, 基于NPLS技术拍摄了无控和控制状态下的混合层流场图像. 通过比较各流动状态下混合层的层流段长度、 运动速度、 涡结构尺寸和形态, 以及分形分析, 得出了RVGA对超声速混合层的控制机理: 通过斜坡形成的向上(下)反向旋转涡对, 实现隔板边界层和自由流中的流体掺混, 提高隔板边界层的能量, 进而使得混合层的能量分布得以改善, 达到推迟转捩、 改变掺混强度、 提高流动速度和减小涡结构各向异性等目的, 最终, 为带气膜冷却光学窗口气动光学效应抑制提供理论支撑. 在本文的实验条件下, 混合层流动速度提高了5%～15%,y1/2处的层流段长度增加了12.8%, K-H不稳定涡的平均波长减小了 5%～30%.

致谢感谢自然科学基金(11832018, 12102463)、 湖南省自然科学基金(2021JJ40652)、 国防科技大学科研计划项目(ZK21-19)以及国防科技大学空天科学学院青年人才重大自主研究项目的资助.