天然气热物性的计算

申沛，张华平，唐梨铧

（上海船舶研究设计院，上海 201203）

0 前 言

为了满足氮氧化物和硫氧化物的排放法规，人们一方面进行尾气后处理技术的研发，另一方面采用清洁能源替代传统燃油。 清洁能源可从根本上解决污染排放，得益于廉价、高效、清洁（硫的氧化物零排放），天然气近年来作为船舶燃料被广泛使用。液化天然气（Liquified Natural Gas，LNG）动力船采用的双燃料低速二冲程主机以MAN 公司的GI 高压型和WIN G&D 公司的DF 低压型为典型代表。高压GI 技术采用迪塞尔循环，高压燃气向气缸内喷射并被点火油点燃后燃烧， 天然气进机的状态为30 MPa/45 ℃。低压DF 技术采用奥托循环，天然气进机状态为1.6 MPa/30 ℃。天然气通常以液态的形式进行运输和储存，常压下LNG 的温度约为-162 ℃，将燃料罐中-162 ℃的LNG 转化为特定进机压力和温度的天然气需要一套燃气供气系统 （Fuel Gas Supply System，FGSS），在此系统的热力学流程中，天然气会经历加热、气化、压缩等过程。对于FGSS 的系统设计和流程模拟，天然气的热物性计算尤为重要。 不同产地的天然气所含甲烷、乙烷、丙烷、丁烷和氮气所占的比例不同，摩尔百分比见表1。 此外，计算LNG 储罐蓄压时间时， 天然气焓值和密度等物性参数的准确性会对计算结果产生较大的影响。

表1 天然气各组分的摩尔百分比

关于天然气热物性的研究大多基于石油化工领域。 刘璐等［1］使用LKP 方程对天然气的密度、焓和熵值进行计算，在压力为1 MPa、温度为120 K 时的计算结果和实验结果误差均控制在5%以内。 杨帆等［2］采用PR 方程计算了天然气的密度和黏度，计算工况为（6.5 MPa，-60 ℃）和（4.5 MPa，-80 ℃），将计算值和实验值对比后发现，PR 方程在黏度计算上比Lucas 法精度要高，在密度计算上，第一种工况下LKP 法误差小，第二种工况下PR 法误差小。 田士章等［3］采用BWRS 方程计算LNG 接收站需求的物性，实例验证结果表明，计算结果可靠，可满足接收站物性计算的要求。 李冉等［4］采用Aspen HYSYS 软件分析评价PR、SRK、LKP、BWRS 状态方程在天然气热力学参数和气液平衡预测的表现，PR 方程的表现最好。 蒋康涛等［5］总结了多种以甲烷为代表的超临界LNG 热物性参数的计算方法，其中热力学性质计算以状态方程法为重点，迁移性质计算主要是对应态方法。

综上，在不同压力和温度条件下天然气的物性计算是FGSS 和LNG 液货系统设计的基础。 天然气物性的实验数据是有限的， 很难覆盖到所有压力、温度区域和所有天然气组分，因此以实验数据为参照，将相同工况下采用不同状态方程得到的计算值与之比较，进而分析总结各个模型在不同工况范围内的精确性。

1 物性计算方程

描述非理想流体的状态方程主要分为两类：立方型状态方程和多参数状态方程。

立方型状态方程是半经验半理论的状态方程，包括RK 方程，SRK 方程，PR 方程，PR-BM 方程，RKS-BM 方程。 通常是如下形式：

式中：P 为压力；R 为通用气体常数；T 为温度；V 为摩尔体积；α（Tr）是变量为相对温度和偏心因子的函数。 其余参数在不同状态方程中取不同的常数，详细参数值见文献［6］。 立方型状态方程可通过直接迭代法或牛顿迭代法求解。

BWR 方程是在维里方程的基础上发展出的多参数方程，它是有严格理论基础的方程。

式中：ρ 为密度；A0、B0、C0、a、b、c、α 和γ 8 个常数由纯物质的p-V-T 数据和蒸气压数据确定。 以提高BWR 方程在低温区域的计算精度为目的，Starling等人提出了11 个常数的Starling 式 （或称BWRS式）， 扩大了方程的应用范围。 Lee 和Starling 将BWR 方程进行普遍化而得到的方程成为BWR-LS方程，可以用于非极性组分，而且可模拟包含氢的系统。

PSRK 方程使用Redlich-Kwong-Soave 状态方程计算纯化合物性质。 混合规则是预测性的H olderbaum 规则或PSRK 方法。在PSRK 状态方程模型中可以使用几种α 函数以便更精确地计算纯组分性质。 PSRK 方法是修正的Huron-Vidal 混合规则的一个例子。 Holderbaum 和Gmehling 开发的这些混合规则在过剩Helmholtz 能和状态方程之间使用了一个关联式， 感兴趣的读者可参阅文献［7］。 混合物的气液平衡即为组分i 在气相和液相中的逸度相等， 要想在气液平衡计算中得到准确结果，必须使用二元参数，本文采用不同状态方程的计算基于ASPEN Plus 软件的二元交互参数数据库。

2 密度计算

密度是随压力、温度和组分变化的，管道流速和压降等参数的计算与密度相关。 同时密度也是FGSS 设计和设备选型中最为重要的参数。 天然气是多种烃类组成的混合物，分子间的作用力、分子的尺寸和极性等都与单质有着本质上的区别。 尤其是在高压条件下， 需要考虑不同组分间的混合规则。

Lentner 等［8］采用磁力悬浮密度计来测量天然气密度，测量条件的温度范围是105～135 K，压力范围是0～8.9 MPa。 图1 展示了5 种不同组分天然气的密度压力关系，图1（a）、（b）、（c）、（d）、（e）中天然气的摩尔组分百分比对应表1 中1、2、3、4、5。从图1 可以看出，在相同温度下，密度的实验值和计算值均随着压力的升高而增大。 在相同压力下，密度的实验值和计算值均随着温度升高而减小。 从图1（a）可以看出，在温度为115 K 时，采用BWR-LS方程和BWRS 方程计算天然气密度的结果与实验值最为接近，计算值均大于实验值。 由于BWR-LS 方程和BWRS 方程计算结果较为接近，图1（a）和1（d）中这两个模型的数据点略有重叠； 在温度为125 K 时，BWRS 方程的计算值与实验结果最为接近， 计算值小于实验值； 在温度为135 K 时，BWR-LS 方程和BWRS 方程计算天然气密度的结果与实验值最为接近，BWR-LS 方程计算值大于实验值， 而BWRS 方程计算值小于实验值。 综合所有工况下的计算和实验结果的对比，BWR-LS 模型的表现最好，PR-BM的误差最大。 由于文献［8］中实验数据较多，温度为105 K、120 K 时，不同方程的计算偏差（|计算值-实验值|/实验值）由表2 列出。 高压下不同方程的计算误差基于文献［9］中的实验数据，压力范围是0～37 MPa，温度范围是250～450 K，天然气的摩尔组分为表1 中的6～9， 此时天然气处于气态和气液共存态，在表2 中给出不同状态方程的计算误差。 在高压工况下，平均误差最小的为BWRS 状态方程误差在5.6%以内，BWR-LS 方程的误差在5.3%以内。PR-BM 方程在高压工况下的计算精确度要好于低压下，在高压工况下，平均误差为1.172 4%，所有数据误差均在7.65%以内。 高压下PSRK 状态方程的精确度最低。

表2 5 种状态方程天然气密度计算的相对误差

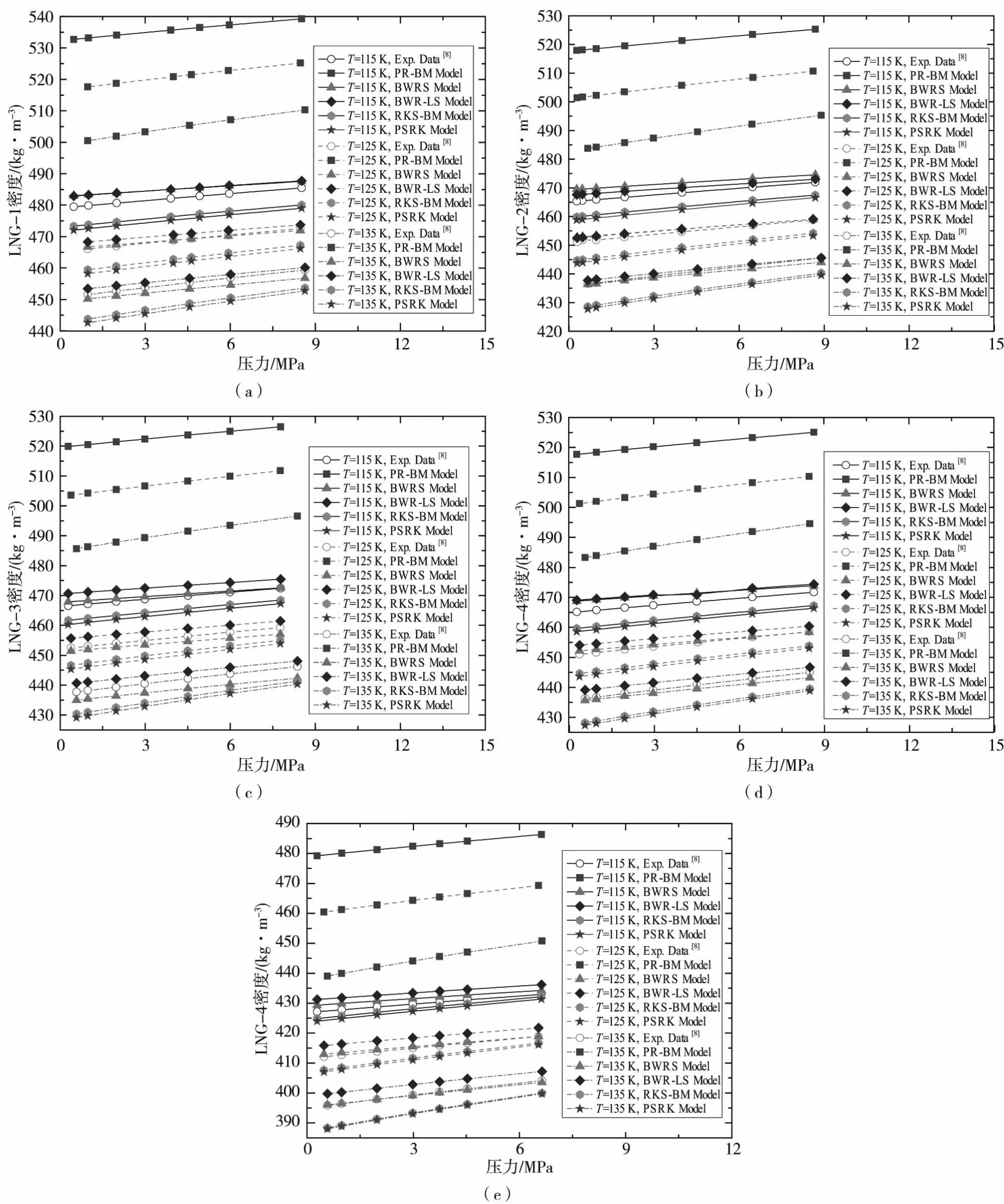
图1 天然气密度的计算值与实验值对比

图2 中由下至上的3 组曲线分别是密度为4 mol/L、8 mol/L、12 mol/L 的 等 密 度 曲 线，其 中12 mol/L 的等密度线不同模型的计算值与实验值均比较接近，数据点在图2 中略有重叠。 实心圆代表文献［10］中的实验数据，温度范围是225～350 K，压力范围是6～35 MPa，天然气的摩尔组分见表1 中的10。与实验等密度线吻合最好的是PR-BM 方程。在6～10 MPa 压力范围下，不同模型的计算偏差不太明显，与实验数据均吻合较好。 在压力较高的工况下，见图2 中8 mol/L、12 mol/L 的等密度曲线， 与实验数据的偏差从小到大依次为PR-BM 方程、BWRS方程、BWR-LS 方程、RKS-BM 方程、PSRK 方程。

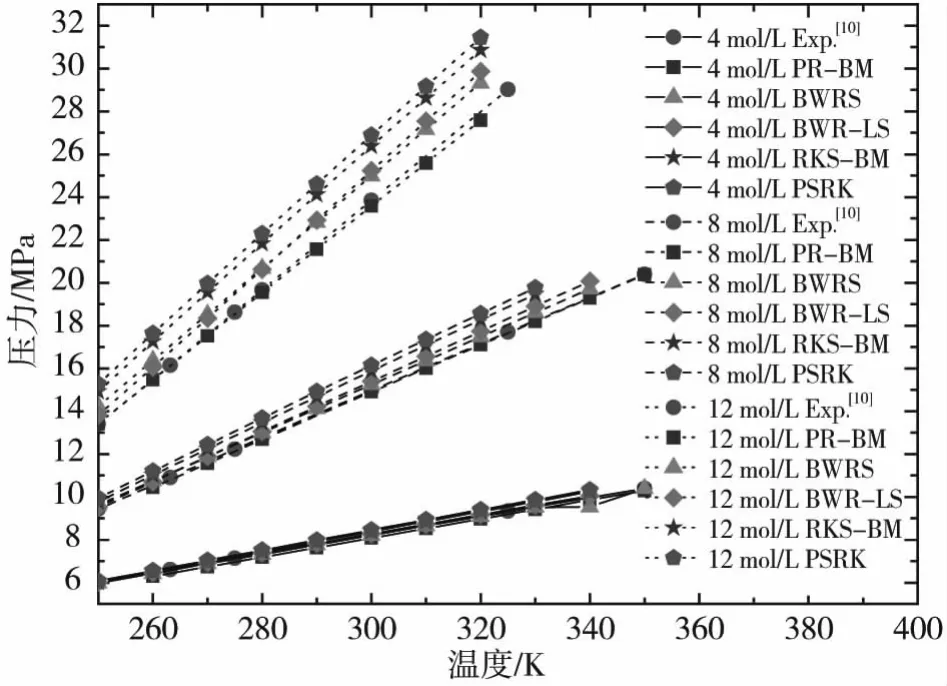
图2 压力-温度图中的等密度线

3 相包络图

露点和泡点是针对混合物的概念，二者的值通常在不同组分下是不同的。 但对于纯组分而言，露点和泡点的值是相等的，此时称为沸点。 露点和泡点对于天然气气液平衡分析至关重要。 文献［11］给出了3 种不同组分天然气的泡点和露点实验值。 如图3 中所示实心圆为实验数据，其中天然气的组分分别为表1 中的11、12、13。相包络线所包围的区域为气液共存区，左侧为液态区，右侧为气态区。 如图3（a）所示，PR 方程的预测结果和实验数据最为吻合，LKP 模型偏差最大，BWRS 方程预测的同压力下泡点温度较实验值偏小，其余方程均偏大。PR 方程、SRK 方程、LKP 方程同压力下泡点温度较实验值偏大的程度逐渐增加。 如图3（b）所示，LKP 方程的计算值和实验数据最为吻合，BWRS 方程、PR 方程和SRK 方程的同压力下泡点和露点的计算值较实验值均偏小。 如图3（c）所示，同压力下泡点和露点的计算值较实验值均偏小，与实验值的偏差从小到大依次为LKP 方程、SRK 方程、PR 方程和BWRS 方程。 查阅表1 中3 种天然气的摩尔组分，可以推测：在重烃占比较小时，PR 方程的预测最为准确； 在重烃占比较大时，即正戊烷和异戊烷的摩尔组分之和大于1%时，LKP 对于相包络曲线的预测最为准确。

图3 天然气相包络图

4 焓差的计算

在FGSS 系统设计中，换热器的选型和LNG 罐漏热量的计算都要基于天然气的焓值。 焓是一个表征物质系统能量的状态参数， 无法测定焓的绝对值，对热力学来说重要的是焓的变化值，这是可以通过实验测量的，因此，以下通过软件计算和实验数据的焓差值作分析比较。 以实验工况为输入，基于ASPEN 软件计算了39 组焓差数据， 如图4 所示，红色正方形为文献［12］中的实验数据，温度从360 K 左右到190 K 左右，压力为1.3～5.7 MPa，每组数据的天然气组分均不同，甲烷的摩尔含量为70%～97%，氮气的摩尔含量为4%～28%。 左侧纵坐标轴表示焓差，右侧纵坐标轴表示焓差的计算误差。 当焓差为4 500～7 000 J/mol 时， 各状态方程的计算值与实验值吻合度较好，误差均在1.5%以内，如图4 所示，1～17 组数据点略有重合。 当焓差高于7 000 J/mol时，各状态方程计算值的误差波动较大。 PR-BM 方程、BWRS 方 程、BWR-LS 方 程、RKS-BM 方 程 和PSRK 方程对于焓差的平均计算误差分别为2.59%、2.87%、3.15%、3.09%和3.24%。 对于以上给定工况下焓差的预测，PSRK 方程的预测精度较差，PR-BM方程的预测精度最好。

图4 天然气焓的实验值和计算值对比

5 结 语

以美国国家标准与技术研究院和卡塔尔大学等国外研究机构的实验数据为参照， 基于PR-BM、BWRS、BWR-LS、RKS-BM、PSRK 状态方程计算出给定压力温度和摩尔组分下的天然气热物性，分析比较不同状态方程的计算精度，具体如下：

1） 在低压工况下，即压力为8 MPa 以内时，BWR-LS 方程预测天然气密度的精度最高。 在高压工况下，即压力范围是9～35 MPa 时，PR-BM 方程预测天然气密度的精度最高。

2） 对于天然气露点泡点和相包络曲线的计算，在重烃含量较少时，PR 方程的预测最为准确；重烃占比较大时，即正戊烷和异戊烷的摩尔占比之和大于1%时，LKP 方程对于相包络曲线的预测最为准确。

3） 低压下天然气焓值的计算，应用PR-BM 方程、BWRS 方 程、BWR-LS 方 程、RKS-BM 方 程 和PSRK 方程的平均计算误差分别为2.59%、2.87%、3.15%、3.09%和3.24%。 PR-BM 方程的计算精度最高。

船用FGSS 供气系统设计时，推荐使用PR-BM方程进行天然气密度和焓值的计算。