基于客户新装、增容户数关联分析下的区域用电量增长预测
2022-03-30李常生许星煜靳文丽
李常生,许星煜,石 磊,李 扬,靳文丽
(国网甘肃省电力有限公司酒泉供电公司,甘肃 酒泉 735000)
经济的快速发展,电力需求的不断提高,现有容量已经不能满足实际情况。随着客户申请新装、增容的数量不断增加,客户新装、增容也成为电力负荷预测不可忽略的一部分。负荷预测的准确性将直接影响到电力企业投资、电力系统网络布局及运行的合理性。另外,根据准确的电力负荷预测结果可以经济合理地安排电网内部发电机组的启停,保持电网运行的安全稳定性,减少不必要的旋转储备容量,合理安排机组检修计划,保障社会的正常生产和生活,有效地降低发电成本,提高经济效益和社会效益。所以,基于客户新装、增容户数关联分析对电力负荷预测的研究急需开展。
1 区域用电量增长预测方法
本文提出的基于客户新装、增容户数关联性分析下的区域用电量增长预测方法流程如图1所示。

图1 基于客户新装、增容户数关联性分析下的区域用电量增长预测方法流程
首先计算第t年和第t-1年对应月份的电量差值ΔQ和对应月份用户新装增容户数差值Δn之间的皮尔逊相关系数ρxy(Pearson Correlation Coefficient)和斯皮尔曼相关系数rs(Spearman's Rank Correlation Coefficient)。
根据ρxy、rs判断ΔQ与Δn是否存在相关关系。若两变量之间不存在相关关系,则区域用电量预测不必考虑用户新装、增容户数的影响;若存在相关关系,则根据ρxy、rs的相对大小判断两变量之间是否存在线性关系。
当ρxy≈rs时,即|ρxy-rs|<ε,ε是一个很小的正数,变量之间存在线性关系,利用线性回归拟合ΔQ与Δn之间的线性表达式ΔQ=WΔn+b。当ΔQ与Δn之间不存在线性关系时,利用多项式拟合ΔQ与Δn之间的表达式ΔQ=,m是多项式阶数。
2 相关性分析
相关性分析用来分析变量之间的相关关系。常用来描述变量之间的相关关系的指标是皮尔逊相关系数和斯皮尔曼相关系数。
皮尔逊相关系数ρxy用来度量两个变量之间的线性关系。斯皮尔曼相关系数rs反映变量之间的变化趋势的方向和程度。与皮尔逊相关系数相比,斯皮尔曼相关系数评估变量之间的单调关系,不易受到错误值和极端值的影响。
3 回归分析
3.1 线性回归
线性回归分析常用于研究自变量与因变量之间的线性相关性[1]。线性回归拟合参数简单,计算量小,计算速度快,但只能拟合线性关系。
线性回归分析的模型:

式中,βi,i=0,1,2,…,n是回归系数,且与xi,i=0,1,2,…,n无关。
若存在n个独立观测数据[bi,ai1,ai2,…,aim],其中,bi为y的观察值,aij是xij的观察值,i=1,2,…,n,j=1,2,…,m(n>m)。
由式(1)可得:

利用最小二乘估计,使得误差平方和最小,即可得到回归系数β,如式(3):
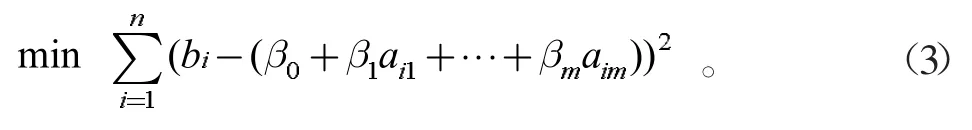
3.2 多项式回归
多项式回归可以拟合变量之间复杂的非线性关系,但多项式回归计算量大,并且多项式阶数不易确定,计算速度慢[2]。
多项式回归分析的模型:

式中,βi,i=0,1,2,…,m是回归系数,m是多项式阶数。
假设目前存在n组数据样本(x1,y1)、(x2,y2)、…、(xn,yn)。其中,yi为第i个样本的输出真实值,y^i为根据式(4)拟合的输出值(i=1,2,…,n),最小化损失函数,如式(5),即可得到最优拟合参数β。

3.3 评估指标
3.3.1 均方误差
均方误差(Mean Squared Error,MSE)反映了预测数据与原始数据之间的差异。
3.3.2 拟合优度
拟合优度是指回归曲线对观测值的拟合程度,反映了回归曲线对观测值信息的利用程度。度量拟合优度的统计量是可决系数R2。R2越接近1,说明回归曲线的观测值拟合程度越好。假设目前存在n组数据样本(x1,y1)、(x2,y2)、…、(xn,yn)。其中,yi为第i个样本的输出真实值,y^i为拟合值(i=1,2,…,n)。定义两个指标:总平方和SST和回归平方和SSR,如式(6)。

可决系数R2的公式:

4 算例分析
本文选取3个典型地区电量数据,时间范围为2017年1月到2019年12月,共36个数据点,包括月份用电量和当月用户新装、增容户数。
电量差值ΔQ与用户新装、增容户数差值△n的相关系数见表1。

表1 ΔQ与Δn的相关系数
由表1可以看出,地区1的ΔQ与Δn没有相关关系,所以在用电量预测时,可以不用考虑用户新装、增容户数对用电量的影响。地区2的ρxy和rs都比较大,且两者的值接近,所以地区2的ΔQ与Δn有强线性关系,可以用线性回归拟合。地区3的ΔQ与Δn具有相关关系,但ρxy明显小于rs,所以两者可以用多项式拟合。
调用matlab2018a工具箱cftool对地区2进行线性回归拟合,如图2所示。
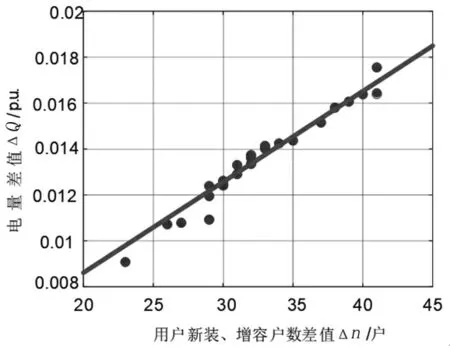
图2 地区2ΔQ与Δn的线性回归图
图2中,在置信度为95%的情况下,拟合直线为ΔQ=0.000395Δn+0.000716。拟合结果的MSE=1.741×10-6,R2=0.902,可以准确地根据地区2的Δn预测出ΔQ。
调用matlab2018a工具箱cftool对地区3进行多项式回归拟合,如图3所示。
图3中,拟合曲线的最高项为3次项,系数拟合在置信度为95%的情况下,拟合曲线表达式如式(8):
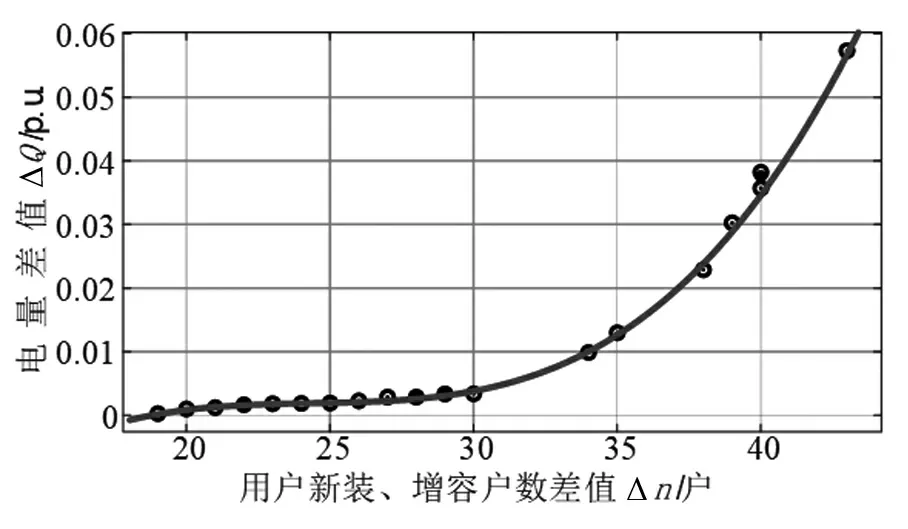
图3 地区3ΔQ与Δn的多项式回归图

拟合结果的MSE=0.001,R2=0.996,可以准确地根据地区3的Δn预测出ΔQ。
5 结论
基于受到客户新装增容的影响,电量的变化是单调变化这一假设,本文提出基于客户新装、增容户数关联性分析下的区域用电量增长预测方法。利用皮尔逊相关系数和斯皮尔曼相关系数,确定ΔQ与Δn之间的相关关系,并针对不同情况选择不同方式拟合两者的表达式:若ΔQ与Δn线性相关,则使用线性拟合,避免复杂的多项式计算;若ΔQ与Δn非线性相关,则使用多项式拟合,确保得到Δn与Δn之间精确的表达式。最后通过算例分析证明了该方法的有效性。
