输电塔-线体系的风致动力稳定性分析
2022-03-30凌晓斌杜伟周转高玄齐益赵宝成
凌晓斌, 杜伟, 周转, 高玄, 齐益, 赵宝成
(1.国网黄山供电公司, 黄山 245000; 2.安徽华电工程咨询设计有限公司, 合肥 230061; 3.苏州科技大学土木工程学院, 苏州 215011)
架空输电线路主要由输电塔和导、地线构成。随着经济、技术的发展,架空输电线路的覆盖面日益扩大,其高度与跨度不断增加,输电塔-线结构体系同时承载了高耸和大跨柔性结构的安全需求。目前,输电塔和导地线风荷载的计算主要根据《架空输电线路荷载规范》(DL/T 5551—2018)[1]的等效静力方法,利用阵风系数和档距折减系数考虑脉动风对导地线风载影响、利用风荷载脉动折减系数考虑结构敏感性和塔线叠加相关性。然而输电塔结构在竖向力和侧向力共同作用时,其抗侧移能力会因结构动力失稳而显著降低,基于静力计算的强度设计不能反映结构的稳定性。因此,输电塔-线结构在风荷载作用下的动力稳定性研究具重要的工程意义。
现有输电塔研究主要包括输电塔优化设计方法[2]、各类型输电塔-线体系风致的动力响应[3-6]、多因素与风载耦合条件下的动力响应[7-8]、导线舞动动力特征[9-10]及台风等极端天气下的动力响应[11-13]。李庆伟等[14]采用B-R(Budiansky-Rot)准则和增量动力分析法(increment dynamic analysis, IDA)结合位移相等原则分析了沈阳某输电塔在风载作用下的动力稳定性。夏闯娜[15]利用ANSYS有限元分析了输电塔-线体系的非线性静力稳定性。李正良等[16]利用气弹性风洞试验和有限元模拟研究了输电塔线体系风振响应,对现行规范风振系数计算方法提出了改进建议。
目前,输电塔-线结构的风致动力稳定研究尚不成熟。为此,基于B-R准则[17]研究不同水平档距输电塔-线结构的风致动力稳定性。通过杆塔顶部侧移比、杆件应力、导地线挂线点反力、张力和振幅变化规律分析了塔-线相互作用及结构动力失稳前、后的受力特征。根据非线性静力与动力失稳塔顶侧移比相等原则得到了不水平档距塔-线结构动力失稳临界平均风速,分析了水平档距对输电塔动力失稳的影响。
1 有限元建模
研究输电塔为安徽某220 kV猫头型悬垂塔,杆塔两侧高差为0,水平档距相同。输电塔呼称高42 m,总高49 m,主材、斜材与辅材均为等边角钢,主材和部分斜材为Q345钢材,其余为Q235钢材。杆塔单线如图1所示,导、地线型号分别为JL/G1A-400/35、JLB20A-150,参数信息如表1所示。

①~⑨为输电塔9区段编号图1 输电塔单线图Fig.1 Single line diagram of transmission tower

表1 导地线参数Table 1 Conductor and ground wire parameters
塔-线结构模型为单塔两档,利用ABAQUS软件进行有限元模拟,有限元模型如图2所示,x、y和z方向分别对应导地线纵向、风攻向和塔高方向。杆塔单元为梁单元B31,导、地线单元为桁架单元T3D2,设定T3D2单元只能受拉;材料本构模型为理想弹塑性;塔脚为刚接,导地线两端为铰支座,中点与输电塔悬挂点用属性为“Join”的连接单元连接,忽略绝缘子串响应。杆塔梁单元截面尺寸及截面方向与实际一致,材料塑性应力取屈服强度;导地线塑性应力取拉断力对应应力,地线截面面积与实际相同,二分裂导线等效为一整体[18],材料阻尼α取0.1、β取0。
有限元计算包括塔-线在重力下导地线找行分析和塔-线在风载下的非线性隐式动力分析。找形分析采用直接迭代法[19]。输电塔和导地线重力包括自重和覆冰荷载,其中覆冰荷载按照杆件覆冰厚度等效为杆件密度,以重力方式施加[20]。杆塔和导线覆冰厚度为15 mm,地线覆冰厚度为20 mm。风载响应采用非线性隐式动力分析,将输电塔按垂直高度分为9段(图1),每段按其中点高度计算风压,将各高度脉动风速时程与平均风速叠加并考虑输电塔的体型系数得到风压,将风压乘以该段受风面积并除以加载单元节点数,得到单元节点上的力。杆塔9区段中点高度分别为3.5、13.5、21、27、30、36、39.5、43.5、47.5 m,导地线节点力计算方法与杆塔相同,风压计算高度取悬挂高度与弧垂高度的平均值。风向角为0°,加载方向为y方向。脉动风速时程采用线性滤波法中的自回归法(auto-regressive,A-R)模拟[21],利用MATLAB计算得到高50 m的空间脉动风速时程。
塔-线体系的动力稳定研究包括递增平均风速IDA分析和基于弧长法(Riks)的非线性静力稳定分析。塔-线水平档距分别取250、300、350、400、450 m,IDA分析对应10 m高度平均风速为20、22、24、26、28、30 m/s。Riks分析用于与IDA分析结果对比,平均风速取28 m/s,风压依据文献[1]计算。塔-线算例名称及其设计参数如表2所示。

图2 输电塔-线结构有限元模型Fig.2 Finite element model of transmission tower line structure
导地线找形分析采用直接迭代法:①首先初步确定导地线原长建立直线模型,在导地线两端施加一定预拉力;②施加导地线和杆塔重力;③释放预拉力;④判断是导地线弧垂、张力与实际间的误差是否满足,若不满足则重复①~③直至满足。为提高建模和找形效率,采用Python编写代码完成ABAQUS的建模-找形-迭代,将导地线弧垂与张力作为判断条件,规定有限元计算与实际误差小于5%。档距250、300、350、400、450 m塔-线结构导、地线找形结果如图3所示,弧垂分别为6.15、8.74、12.1、15.9、20.2 m,与工程实际测量弧垂误差小于2%。

表2 塔-线算例参数Table 2 Tower line example parameters
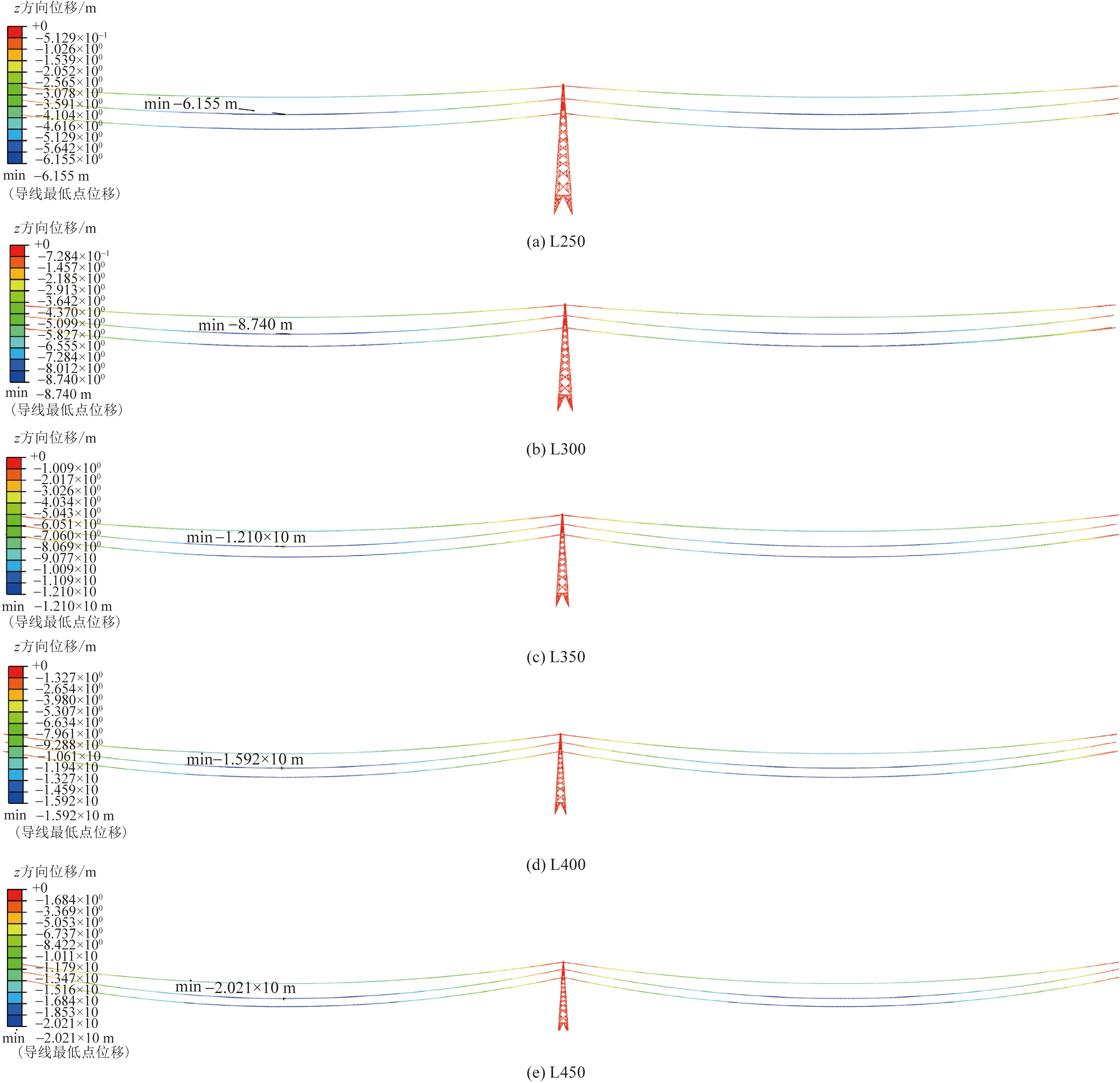
图3 导地线找形结果Fig.3 Shape results of conductor and shield wires
A-R法风速时程模拟基本假设为:①任意一点处平均风速不随时间改变;②脉动风速时程是零均值、平稳高斯过程;③风速时程具有空间相关性;④不同高度处的脉动风速作用同相。脉动风时程的目标功率谱为Davenport功率谱,相干函数采用Davenport相干函数,自回归阶数取4。同一平均风速包括50 m高度内、增量0.5 m的100条脉动风速时程,每条脉动风速时程持时204.8 s,时间间隔0.1 s,取0~200 s作为荷载数据。图4(a)和图4(b)分别为高度10 m处风速时程及其自功率密度谱与目标功率谱的对比,可以看出风速时程符合脉动风特征,其自功率谱变化趋势与目标谱基本一致,且目标谱基本位于模拟谱中部,说明该空间风速时程可用于本研究。

图4 脉动风模拟对比Fig.4 Comparison of fluctuating wind simulation
2 输电塔-线结构失稳特征
以300 m档距为例,结合IDA和Riks分析塔-线结构的风致响应及动力失稳前、后的受力特征。图5为L300-V20-D~L300-V30-D塔顶侧移比时程曲线,塔顶侧移比D/H随时间变化呈脉动趋势,D/H-时间曲线的振幅随平均风速增加而增大。L300-V20-D塔顶侧移比在107.2 s时达到最大值0.41%,L300-V22-D塔顶侧移比在107.8 s时达到最大值0.58%,L300-V24-D塔顶侧移比在155.3 s时
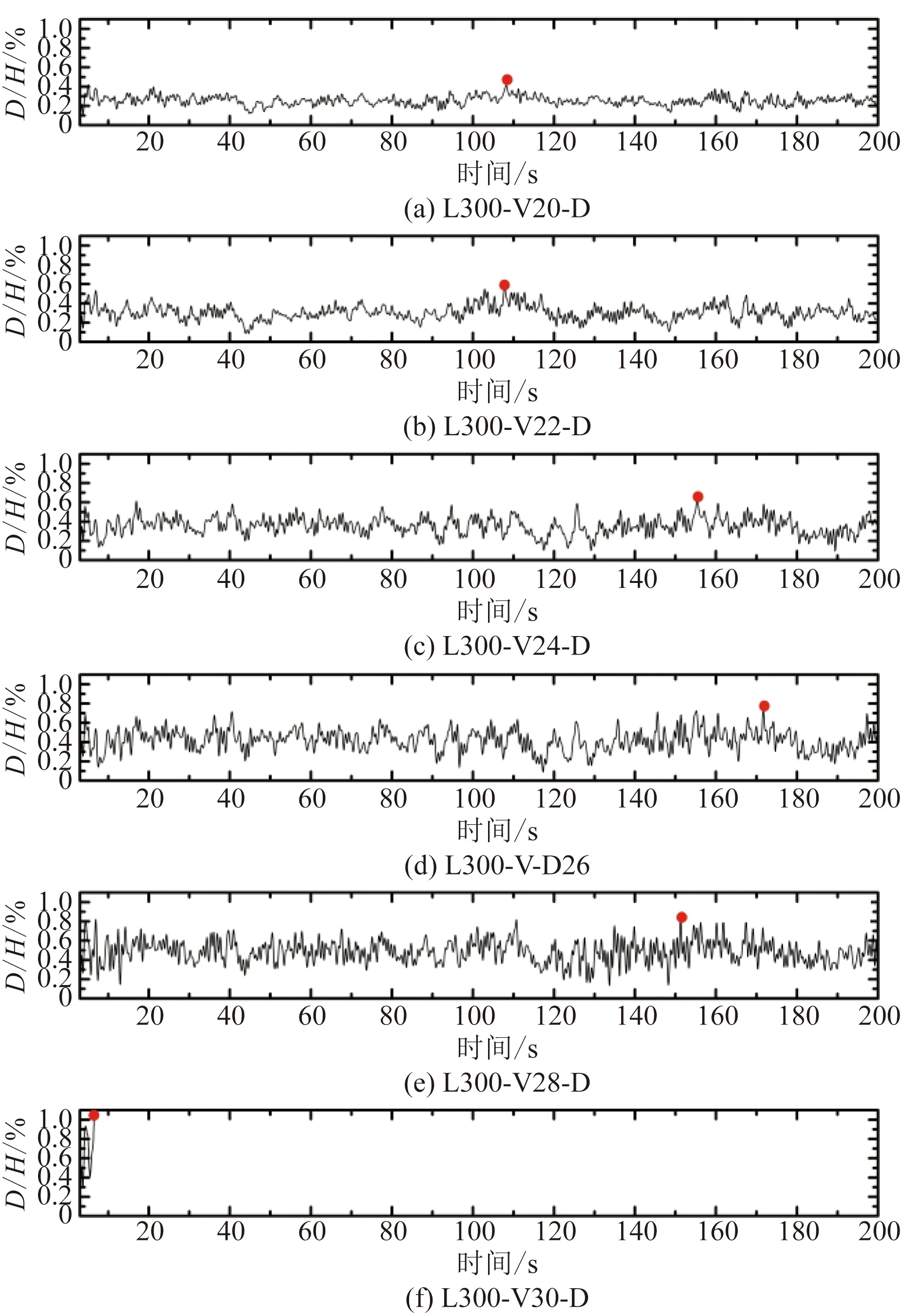
D/H为塔顶侧移比,其中,D为塔顶侧移,H为塔高;红点为塔顶侧移比最大值图5 L300-Vi-D塔顶侧移比时程Fig.5 L300-Vi-D tower top drift ratio time-histories
达到最大值0.62%,L300-V26-D塔顶侧移比在171.7 s时达到最大值0.74%,L300-V28-D塔顶侧移比在151.3 s时达到最大值0.84%,L300-V30-D塔顶侧移比在6.4s时达到最大值0.98%。
分析各算例应力分布知,塔顶侧移比较大导致塔身受压侧主材应力较大,图6显示了L300-Vi-D受力较大杆件的Mises应力时程曲线,受力较大杆件均为塔身底层受压侧主材。可以看出,各算例杆件应力变化规律及最大值时刻与塔顶侧移比时程曲线几乎相同。值得注意的是:L300-V26-D杆件应力最大值328.5 MPa接近材料屈服强度;L300-V28-D杆件应力在4.3、6.8、110.8、161.8 s均达到材料屈服强度345 MPa;L300-V30-D杆件在6.4 s第二次达到屈服强度后开始下降。
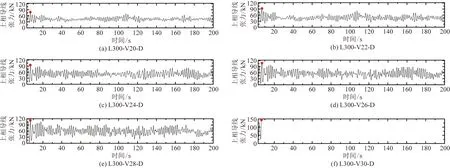
分析各算例导地线受力情况知,上相导线挂线点反力及其张力较大,相应时程曲线分别如图7、图8所示。可以看出,上相导线响应速度要明显滞后于杆塔,随着平均风速增加,上相导线挂点反力及张力幅值逐渐增大。如图7所示,L300-V20 -D~L300-V30-D上相导线挂线点反力最大值分别为17.8、21.2、
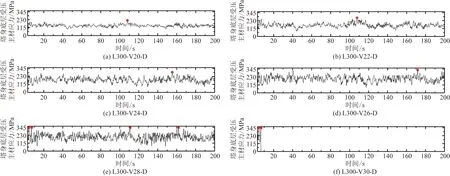
红点为应力最大值图6 L300-Vi-D塔身底部受压杆件应力时程Fig.6 Mises stress time-histories of L300-Vi-D pressure bar at the bottom of tower body

红点为表示挂线点反力最大值时刻与杆塔顶侧移比及塔身底层受压主材应力最大时刻不一致图7 L300-Vi-D上相导线挂线点反力时程Fig.7 Reaction force time-histories of phase conductor hanging point on L300-Vi-D
红点表示最大值时刻基本集中在7 s左右,与挂点反力最大值时刻不一致图8 L300-Vi-D上相导线张力时程Fig.8 Conductor tension time-histories of L300-Vi-D
22.5、24.5、27.6、37.2 kN,挂线点反力最大值时刻与杆塔顶侧移比及塔身底层受压主材应力最大时刻不一致。如图8所示,L300-V20-D~L300-V30-D上相导线张力时程曲线变化规律与其挂线点反力时程曲线变化规律相近,张力最大值分别为74.9、90.0、97.7、107.6、118.6、134.1 kN,最大值时刻基本集中在7 s左右,与挂点反力最大值时刻不一致。
导地线在风荷载作用下的振幅基本与弧垂相同,随平均风速的增大略有增加。L300-V24-D上相导线运动轨迹如图9所示,导线在风荷载和重力作用下向沿塔高和风攻方向运动,最大振幅约为11.6 m,略大于弧垂8.8 m。

图9 L300-V24-D上相导线运动轨迹Fig.9 Upper conductor motion curve of L300-V24-D
分析可知,杆塔和导地线在风荷载下的响应存在明显差别,因此分析二者响应较大时刻杆塔的应力分布规律。图10(a)为L300-V26-D上相导线挂点反力最大值时刻杆塔Mises应力分布,可以看出挂线点横隔主材已达到屈服强度345 MPa。图10(b)为L300-V28-D塔身底层受压主材应力最大时刻杆塔Mises应力分布,可以看出塔身底层受压侧主材大部分达到屈服强度。图10(c)为L300-V30-D 6.4 s时杆塔Mises应力分布,此时塔身底层至三层受压侧主材、斜材严重变形,横担挂线处主材达到屈服强度。
塔-线结构动力失稳的过程可总结为挂线点主材屈服-塔身底层受压主材屈服-塔顶侧移比增大-杆塔底部严重变形,而杆塔失稳的临界状态较难判断。图11对比了杆塔Riks(L300-V28-S)与IDA分析得到的标准高度平均风速-塔顶侧移比(D/H)曲线,L300-V28-S在平均风速24.8 m/s时出现拐点,塔身底层受压侧主材屈服;在风速25.2 m/s时Riks运算结束,塔身顶层受压侧主材弹塑性屈曲,对应塔顶侧移比0.57%。IDA曲线在前期与Riks曲线几乎重合,在平均风速20 m/s时出现拐点,此后二者差别增大。与动力失稳特征相比,非线性静力失稳前杆塔挂线点周边杆件未进入塑性,且杆塔受压侧主材进入塑性较早。根据位移相等原则,以塔顶侧移比0.57%定位IDA曲线上的平均风速,得到档距300 m塔-线结构动力失稳临界风速为22.8 m/s。

图10 应力分布Fig.10 Stress distribution

图11 300 m档距标准高度平均风速-D/H曲线Fig.11 Basic wind speed-D/H curves of 300 m span
3 塔-线动力稳定参数影响分析
综合IDA与Riks运算结果,分析不同档距输电塔-线结构的动力稳定,通过Riks与IDA临界塔顶侧移比相等原则得到输电塔动力失稳临界平均风速。图12(a)为L250标准高度平均风速-D/H曲线,L250-V28-S曲线在前期线性增长,风速为21.8 m/s时出现拐点,塔顶侧移比达到0.7%后,非线性静力稳定运算停止,对应风速27.7 m/s。L250-V20-D~L250-V30-D塔顶侧移最大值基本维持线性增长,当平均风速为30 m/s时塔顶侧移比为1.0%,杆塔底层严重变形,非线性动力运算停止。Riks与IDA曲线第一拐点对应风速基本一致,但Riks曲线斜率较小,可见塔-线动力相互作用在结构弹性阶段对稳定有利;当平均风速超过22 m/s后IDA曲线值小于Riks曲线值;按位移等效原则可得L250塔-线临界平均风速为23.9 m/s。
图12(b)为L350标准高度平均风速-D/H曲线,L350-V28-S曲线在前期维持线性增长,塔顶侧移比达到0.56%后,非线性静力稳定运算停止,对应平均风速24.2 m/s。L350-V20 -D~L350-V30-D塔顶侧移最大值基本保持线性增长,当平均风速为30 m/s时,非线性动力运算停止,塔顶侧移比为1.0%,曲线略有突变。Riks与IDA曲线在前期基本重合,可见塔-线动力相互作用在结构弹性阶段并不明显;当平均风速超过20 m/s后IDA曲线值小于Riks曲线值;按位移等效原则可得L350塔-线临界平均风速为21.7 m/s。塔-线算例L400 Riks与IDA曲线[图12(c)]变化趋势及差别与L350分析结果类似,L400 IDA曲线最大风速为28 m/s,Riks曲线最大平均风速为23.4 m/s,塔-线临界平均风速为21.2 m/s,小于L350临界平均风速。
L450标准高度平均风速-D/H曲线如图12(d)所示,L450-V28-S曲线在前期线性增长,风速20 m/s

图12 标准高度平均风速-塔顶侧移比曲线Fig.12 Basic wind speed-D/H curves
出现拐点,塔顶侧移比达到0.56%后,非线性静力稳定运算停止,对应风速22.7 m/s。L450-V20-D~L450-V30-D塔顶侧移最大值基本维持线性增长,当平均风速为26 m/s时,塔顶侧移比为1.0%,动力运算停止。L450 IDA曲线值始终小于Riks曲线值,可见塔-线动力相互作用对结构稳定不利;按位移等效原则可得L450塔-线临界平均风速为21.0 m/s。
对比Riks和IDA曲线可知,随着档距增大,塔-线结构的前期响应经历了静力大于动力、静力约等于动力、静力小于动力的演变过程;在后期响应中塔-线的动力响应均大于静力响应。L250~L450塔-线静力与失稳临界平均风速对比如表3所示,静力和动力失稳平均风速随档距增大而降低,静力与动力失稳平均风速比值随档距变化基本维持在1.1左右。

表3 塔-线静力与动力失稳临界平均风速对比Table 3 Comparison of critical wind speed between static and dynamic analyses
4 导地线动力响应参数影响分析
通过各算例上相导线的挂线点反力、张力和振幅最大值分析水平档距和平均风速对导地线动力响应的影响。图13为上相导线挂线点反力峰值-平均风速曲线,挂线点反力峰值随平均风速增加而增大;同一平均风速下挂线点反力峰值随档距增大而增加,当IDA接近最大风速时(L250、L300、L350为30 m/s,L400为28 m/s,L450为26 m/s)挂线点反力峰值基本一致,约为35 kN,符合第3节分析的塔-线动力失稳特征。
上相导线张力峰值-平均风速曲线如图14所示,导线张力峰值随平均风速增加而增大;同一平均风速下导线张力峰值随档距增大而减小。L250~L450导地线的初始张力相同,但刚度不同,固在风荷载、自重和覆冰荷载共同作用下档距越大导线张力越小。L250~L450上相导线振幅随平均风速变化规律如图15所示,各档距导线振幅随风速增大略有增加,振幅峰值基本略大于弧垂,固档距越大导线振幅越大。
杆塔与导地线相互作用主要反映在挂线点反力和二者运动特性的差异。增加塔-线结构档距,使得杆塔挂线点反力增大,也使得导地线张力减小、导地线振幅增大,导致导地线与杆塔运动特性的差异变大。综合来看,水平档距对于塔、线相互作用及杆塔动力稳定的影响较大,但对输电塔动力放大效应影响不明显。

图13 挂线点反力峰值-标准高度平均风速曲线Fig.13 Hanging reaction peak force-basic wind speed curves

图14 导线张力峰值-标准高度平均风速曲线Fig.14 Conductor peak tension-basic wind speed curves
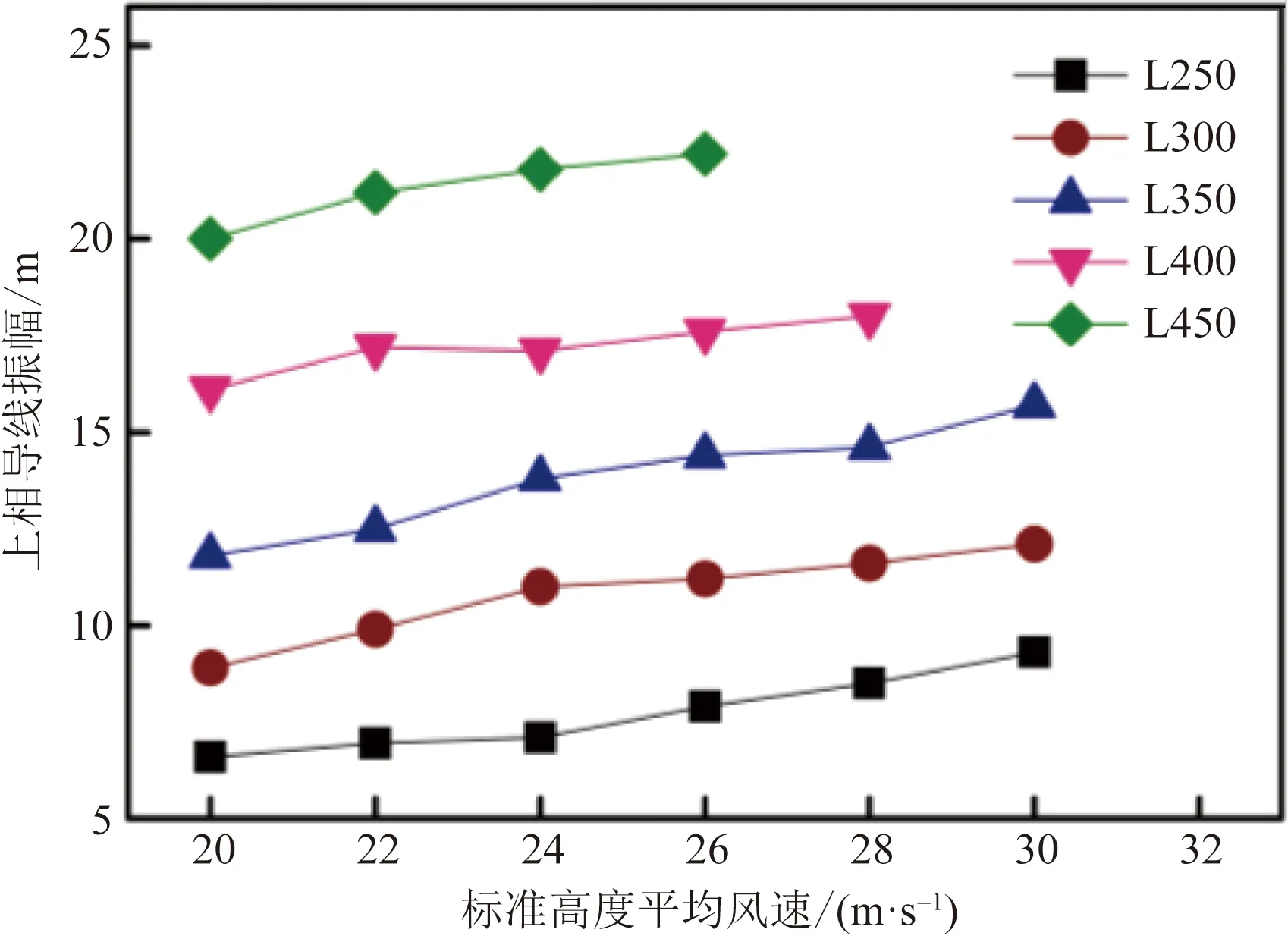
图15 导线振幅-标准高度平均风速曲线Fig.15 Peak conductor amplitude-basic wind speed curves
5 结论
结合增量动力分析法和弧长法对不同水平档距塔-线结构在风荷载作用下的动力稳定进行了研究,通过杆塔和上相导线的动态响应分析了塔-线结构的动力失稳特征,有限元参数影响分析了塔-线的动力稳定。得出如下主要结论。
(1)塔-线结构动力失稳的过程为挂线点主材屈服-塔身底层受压主材屈服-塔顶侧移比增大-杆塔底部严重变形。
(2)随着塔-线水平档距增加,输电塔顶部侧移比增大,挂线点反力增大,导地线张力减小,导地线振幅增大,动力失稳临界平均风速减小。
(3)水平档距对于塔、线相互作用及杆塔动力稳定的影响较大,但对输电塔动力放大效应影响不明显,静力与动力稳定临界平均风速比值约为1.1。
