海上无人集群联合轨迹设计方法
2022-03-30胡钰林原晓鹏
胡钰林 吴 鹏 原晓鹏 李 博 江 昊 罗 威
①(武汉大学电子信息学院 武汉 430072)
②(哈尔滨工业大学(威海)信息科学与工程学院 威海 264209)
③(中国舰船研究设计中心 武汉 430000)
1 引言
海洋大数据的快速积累为海洋可持续发展起到了重要作用。传感器存储的水文、大气、生物活动等数据为海洋开发和保护提供了丰富的决策信息[1]。然而,如何有效地收集传感器的数据是一个关键性问题,尤其是在海况不可控的海域,控制中心无法直接通过无线传输进行设备数据收集[2,3]。因此,为该类型海域研究新的数据收集方法意义重大。
得益于无人机通信技术的高速发展,利用无人机前往危险区域收集设备数据成为一种有效的解决策略[4]。在无线网络中,无人机可作为移动基站,组成多层异构网络,与蜂窝网络无法覆盖的用户进行数据传输[5–7]。由于续航较差,无人机需要定时飞回基地充电,但在辽阔的海面,无人机无法像在陆地一样飞回基地进行能量补给和数据卸载,因此,在海上使用无人机收集数据需要采用新的补给方案。综合无人机的高机动性和高可控性、无人船的运载和续航能力,本文提出“无人船+多无人机”的集群形式,无人船作为移动平台,无人机从无人船起飞前往任务海域收集设备数据,并在需要时刻返回无人船进行补给。
由于无人机具有高机动性,可以为整个通信系统引入更多自由度[8],通过优化无人机的部署位置和飞行轨迹可以与用户设备建立更高质量的通信链路以实现更高速率更低误码率的数据传输。为了提高数据收集的效率,对无人机集群和无人船轨迹的设计成为关键问题。文献[9,10]研究一种基于强化学习的无人机轨迹动态优化方法,该方法侧重根据输入环境的变化动态调整轨迹,无法得到事前最优轨迹,并没有彻底解决无人机最优轨迹优化问题。为了获得无人机的最优轨迹,文献[11]提出将无人机的轨迹离散化求解的方法以实现较优的任务轨迹,但存在计算复杂度过大的问题。为了降低轨迹优化的复杂度,文献[12]忽略无人机速度限制,通过优化多个悬停点来确定无人机的轨迹,该方案只能实现一个次优解。文献[13,14]在考虑到无人机最大速度限制情况下,分别在1维和2维场景实现了低复杂度的最优轨迹设计并通过连续凸近似的方法得到了一个性能较好的次优解,但文章中的方法不能直接应用于2维协作的场景。本文将针对包含无人船和无人机在内的无人集群协同轨迹设计这一开放性问题,首次提出基于用户分组和SHF结构的低复杂度轨迹优化算法,并获得高效的联合轨迹解。
本文结构如下:第2节构建一个海上无人机集群通信模型,提出原始的联合轨迹优化问题;第3节将初始问题分解为用户分组和单无人机轨迹设计两个子问题,在解决子问题的基础上进行问题的重组,并针对重组问题的非凸性,提出连续凸近似的高效迭代求解方法;第4节仿真验证算法的有效性和相对其他算法的优势;第5节总结全文。
2 系统模型
图1为一个海上无人机集群数据收集系统,该系统包括N架无人机,K个传感器用户以及一艘无人船。无人船在从起始点(xα,yα)到目标点(xβ,yβ)航行过程中放飞无人机收集传感器的数据,并在每个无人机的飞行终点回收无人机。无人机飞行高度固定为H,最大飞行速度为V,无人船最大速度为Vp,传感器位置已知,记第k 个用户位置为(wx,k,wy,k),其需要卸载的数据量为Dk。
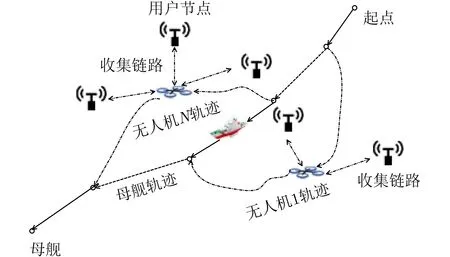
图 1 海洋无人机通信系统
具体而言,对无人机i,其在τi时刻从无人船起飞收集用户数据,总飞行时间为Ti即无人船于τi+Ti时刻回收该无人机。在该无人机飞行过程中,考虑在有限载波资源下情况存在用户调度问题,引入对用户k的调度参数ai,k,有

约束式(3b)表示收集完所有用户数据这一约束,约束式(3c)表示无人机起飞前和回收后与无人船位置应该相同,约束式(3d)为无人船起止点约束,约束式(3e)为无人船和无人机速度约束。注意到约束式(3b)是个非凸约束,该问题其余式子为凸,因此该问题为非凸问题。并且,该问题包含连续时间上的无穷个变量(xi(t),yi(t)),这使得该问题的直接求解十分复杂。有必要对问题进行分解和重组。
3 问题分解与重组求解
原问题的求解难点在于该问题是对连续时间上无穷个位置变量求解的非凸问题,并且存在任务调度问题。因此问题的分解目标在于明确无人机的服务的用户以及实现低复杂度的无人机轨迹优化。本节将原问题分解为基于用户分布的用户分组和单无人机轨迹优化两个子问题,首先引入分组方法K-means,明确无人机的服务用户,消除无人机之间任务约束问题。然后针对单无人机的轨迹设计,通过引入连续悬停飞行结构SHF,将连续时间上无穷个位置变量的优化问题转化为有限个无人机悬停点的求解问题,降低了轨迹求解难度。最后将分解的两个子问题进行重组,针对重组问题的非凸性,采用连续凸近似的方法,最终实现复杂度较低的轨迹迭代算法。
3.1 用户分组

3.2 单无人机轨迹重构

图2 用户分组
在任务分配的基础上,为获得第i(i=1,2,...,N)个无人机的最优轨迹,考虑如图3所示含有Ki个 用户的单无人机服务场景。
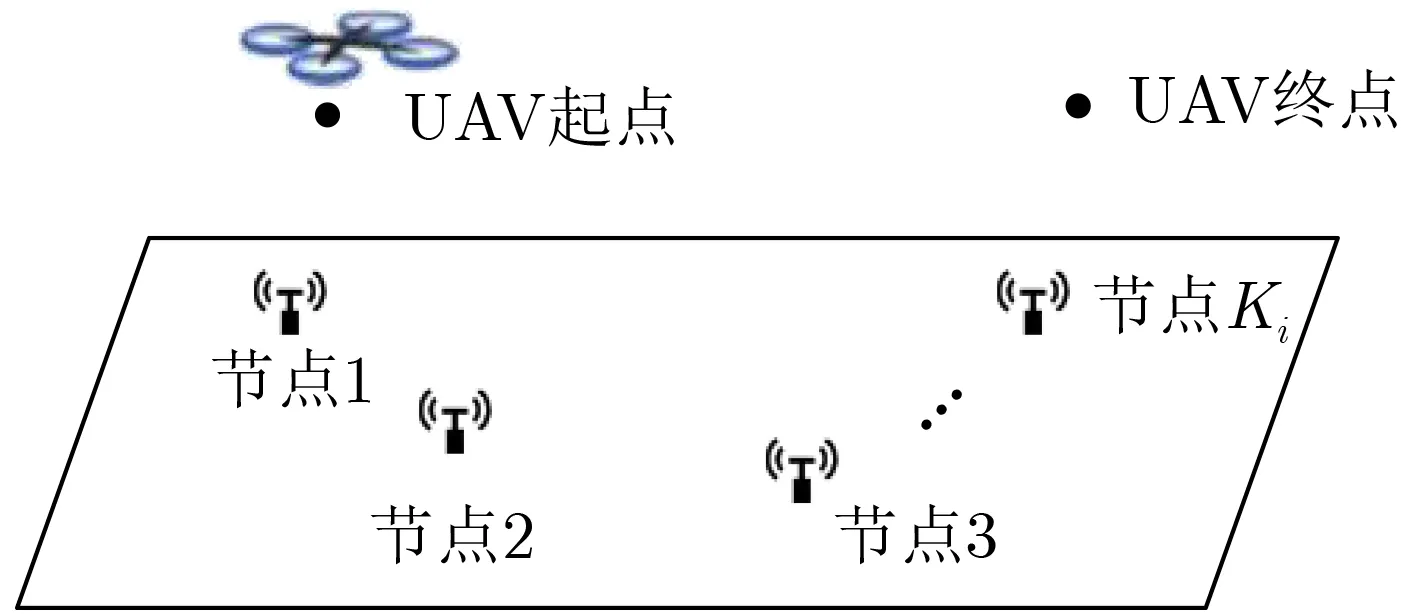
图3 单无人机服务场景示例

令悬停时间矢量为ti,即第j个悬停点(xi,j,yi,j)上悬停时间为ti,j,无人机起止点和悬停点将无人机轨迹划分为Ki+1条弧线,令第j条弧li,j的长为

表1 K-means算法流程
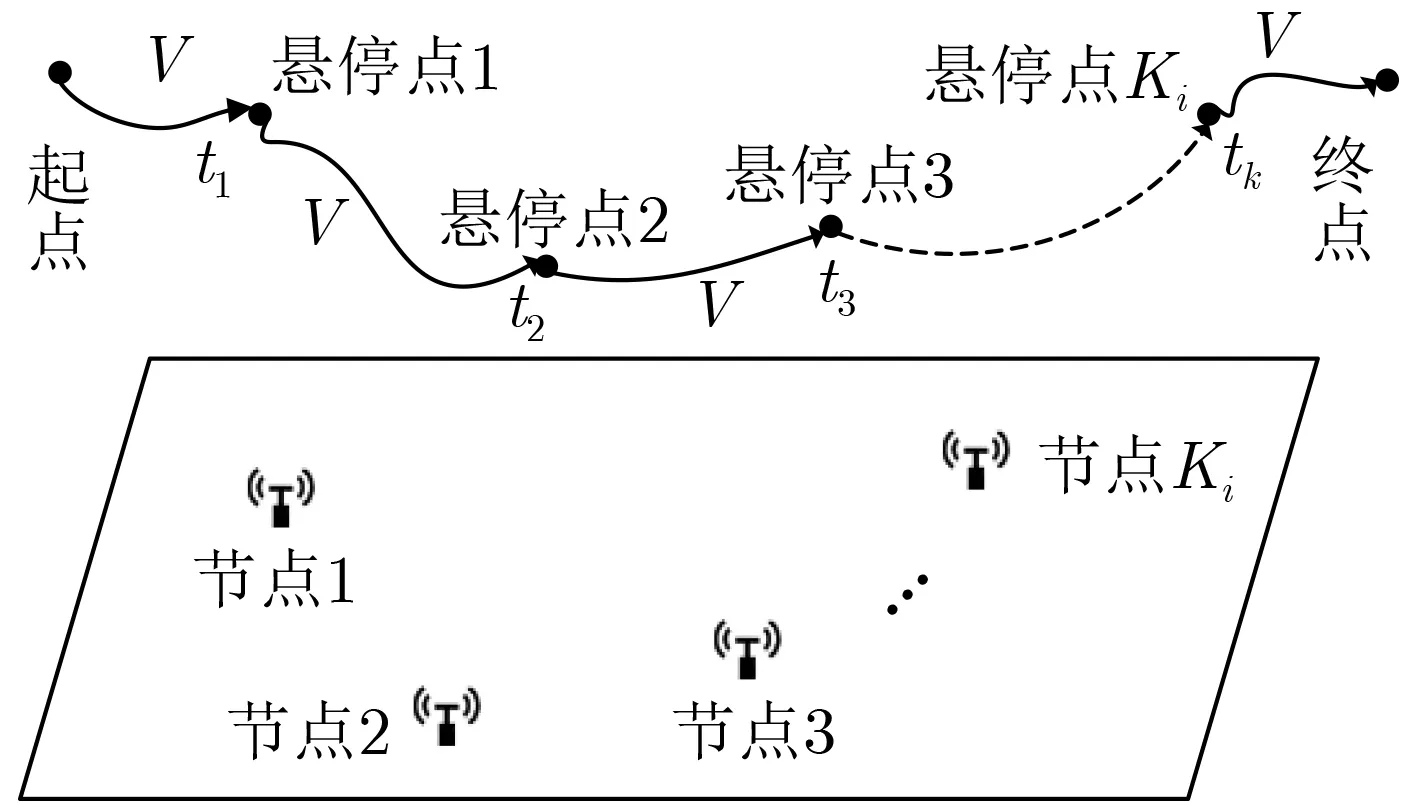
图4 SHF结构下无人机轨迹示例


那么,以起飞时刻作为计时起点,无人机i的轨迹可表示为
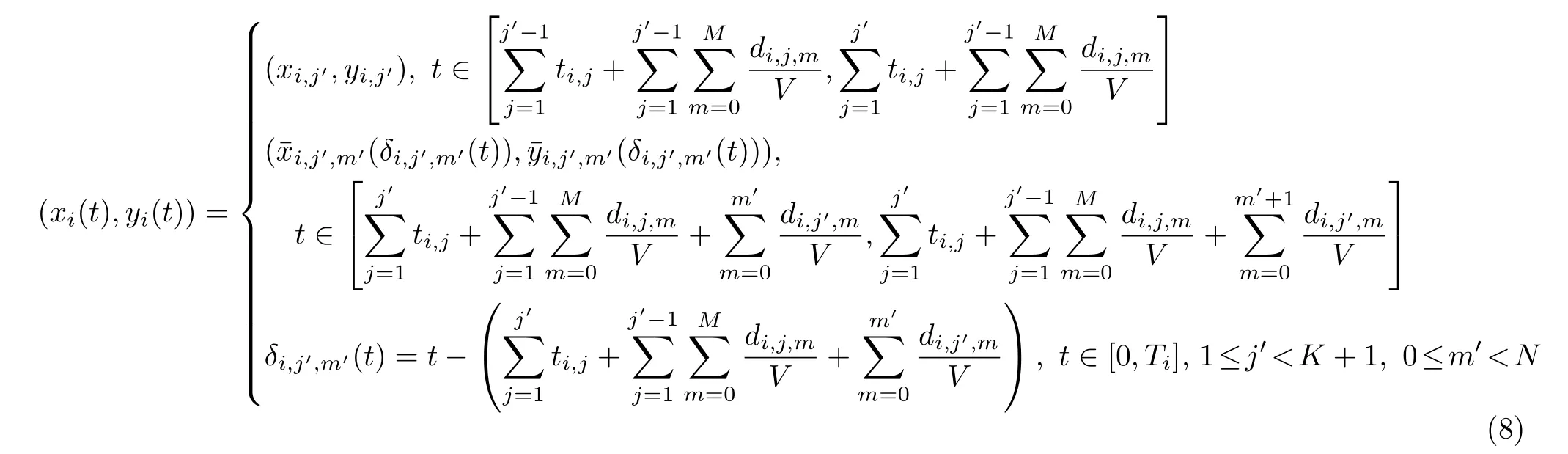

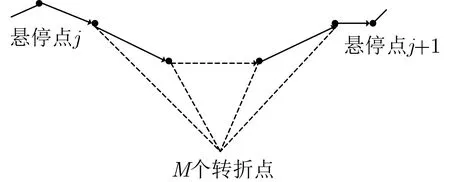
图5 考虑到转折点的SHF结构轨迹示例
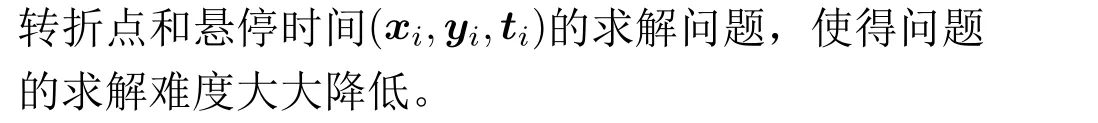
3.3 问题重组与求解
3.3.1 问题重组


3.3.2 连续凸近似
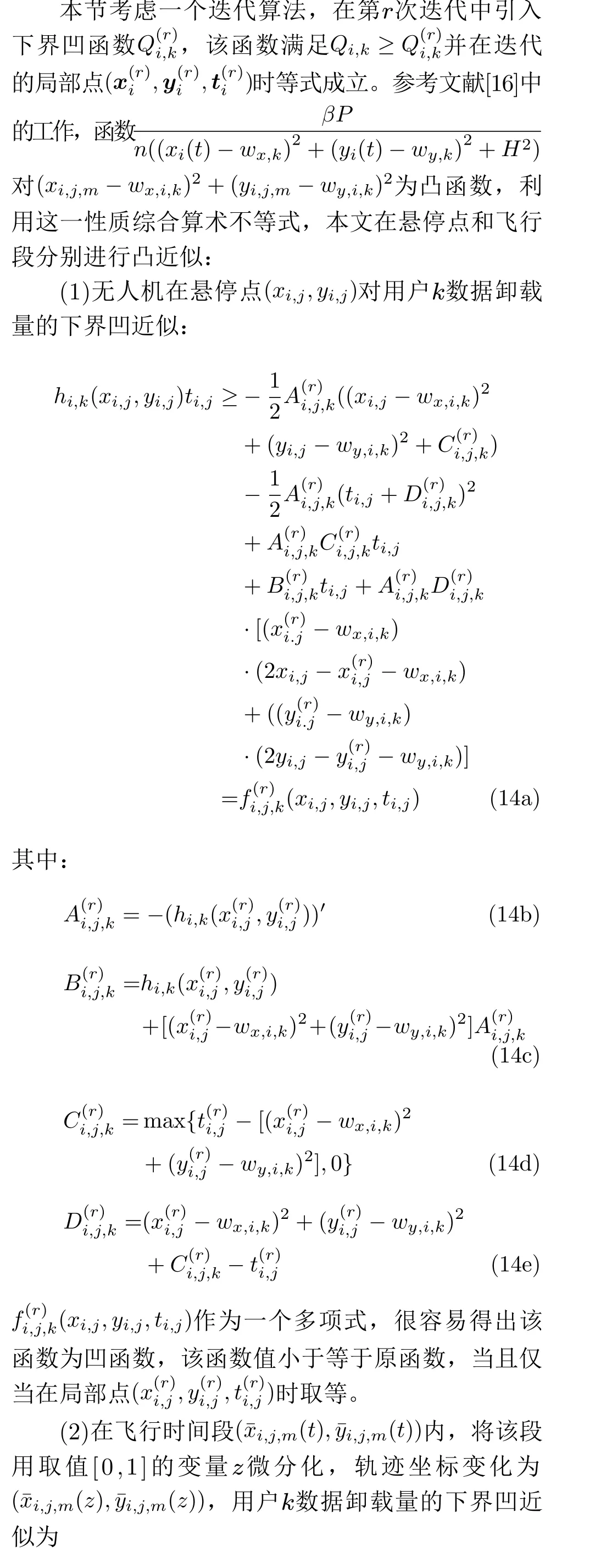


3.3.3 轨迹初始化和轨迹迭代算法

4 轨迹仿真
利用计算机对算法进行仿真,系统参数:无人船的出发点为(0, 0),终点为(3000, 3000) m,无人船速度5 m/s,无人机数目为3,飞行高度为30 m,飞行速度为9 m/s,转折点数目为1,用户节点射频功率10 dBW,噪声功率–60 dBW,信道增益为–30 dB,用户数目为15,数据量从0到100的均匀分布中取值,用户随机分布在任务海域中,图6展示了根据聚类算法实现的用户分组效果图。

图6 用户分组示例

表2 轨迹迭代算法
图7展示了无人机和无人船的联合轨迹,无人船的轨迹为无人机的起止点确定的折线段,无人机轨迹由悬停点和转折点确定。注:考虑到图例数目过多问题,在表述无人机轨迹、悬停点、转折点和起止点时,图例中都用的黑色表示。但在途中用的每架无人机对应的颜色。由于离用户越近,无线传输速率越快,无人机的悬停点趋向于在用户附近分布,可以看出无人机的悬停点几乎与用户位置重合。值得注意的是,放大圈中部分可以发现,虽然悬停点与用户位置距离很近,但两者并不重合,原因如文献[12]所述,无人机的悬停点为原问题拉格朗日方程中对所有用户传输速率总和最大的点,而不是对单一用户传输速率最大的点,因此无人机的悬停点不在用户正上方。

图7 联合轨迹优化示例
图8比较了不同无人机速度下的轨迹。首先图8(a)和图8(b)左侧大图对两种速度下,轨迹的大致形状进行比较。无人机速度改变时,轨迹的大致形状并不发生变化,无人机的悬停点依然在用户附近,这是因为考虑对具体某个用户的数据传输速率,无人机总是倾向于在该用户附近悬停,改变无人机的速度并不会导致轨迹发生巨大变化。图8(a)和图8(b)右侧小图对不同速度下的局部轨迹进行比较。无人机速度越大,悬停点的位置越靠近用户。这是因为在一定的任务时间内,增加无人机的速度能增加无人机向用户的位移。因此,可以通过增加无人机的速度使无人机悬停点更靠近用户,在悬停点获得对该用户更大的数据传输速率,但注意,在该悬停点其他用户的数据传输速率不一定增加,因此整个任务时间不一定减小,图9体现了这一变化趋势。
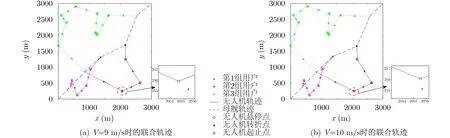
图8 不同无人机速度下联合轨迹比较
图9给出本算法与TSP方法的性能对比,TSP方法通过求解旅行商问题获得通过所有用户节点的最短路径,并在此基础上优化无人机在用户上方的悬停时间。无人机和无人船任务时间分别随无人机速度变化如图9(a)所示,随着无人机速度增加,本算法下无人机和无人船的任务时间波动下降,基于TSP算法的无人机和无人船的任务时间线性下降,并且本算法无人机的任务时间小于TSP算法无人机的任务时间,而两种算法无人船的任务时间几乎一致。TSP方法优化过程中,无人机与无人船轨迹不变,只优化无人机悬停时间的情况下,问题为凸优化问题所求的即是该方案下的最优解,因此任务时间与无人机速度呈现线性关系,而由于本算法在求解过程中采用了连续凸近似的方法,最终获得的联合轨迹为该方案下的一个次优解,因此任务时间与无人机的速度并不呈现线性关系,这并非为算法稳定性差所致。由于本算法同时优化无人机轨迹和悬停时间,比TSP方法更接近于全局最优解,因此本方法下无人机的任务时间远小于TSP方法下无人机的任务时间。由于TSP方法下无人船的轨迹比本方法短,因此无人船的运动时间比本方法短,但由于TSP方法下无人机的任务时间更长,无人船的等待时间更长,因此两种方法下无人船的任务时间相差不大。图9(b)展示了总任务时间与无人机速度的关系,本算法的任务时间随无人机速度变化虽然存在波动,但明显优于TSP优化方法。
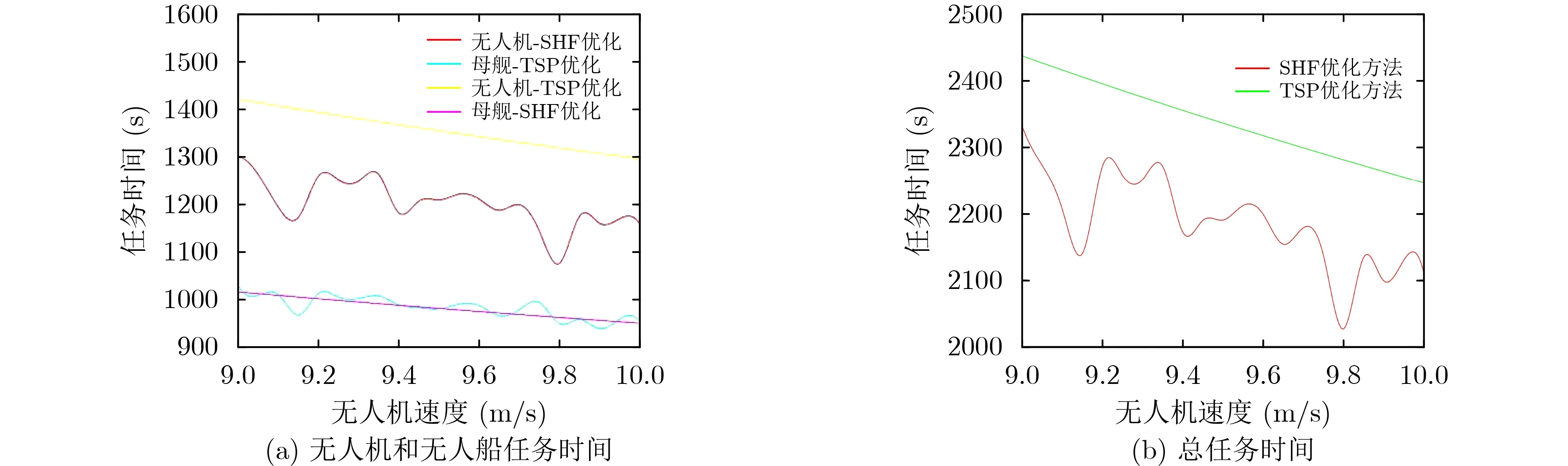
图9 本算法与TSP算法任务时间对比
5 结束语
本文考虑了一个无人机集群与无人船平台联合数据收集系统,在无人机最大速度限制下研究了一个旨在最小化任务时间的联合轨迹设计问题。本文首先考虑到用户任务分配问题,通过分组算法k-means进行用户分组。其次,本文描述了无人机轨迹的2维结构,在此基础上引入SHF结构,将连续时间上无限个轨迹点的优化问题转化为有限悬停点和转折点的求解问题。在此基础上,将原问题重构为一个低复杂度的问题。并引入连续凸近似的方法将非凸问题转化为可高效求解的凸问题。最后通过仿真验证了本方法的有效性。值得一提的是,虽然本文研究的是海洋数据收集场景下的无人机和无人船的轨迹,所提出的无人船(或移动补给台)与无人机的联合轨迹设计思想、问题解构和子问题求解方法都可以拓展到其他(如无线能量传输等)需要无人集群协同工作的联合轨迹设计问题。值得注意的是,在无线能量传输场景下为无人机向空间辐射射频能量,而本文考虑的无线数据收集场景为用户上行传输数据,但在轨迹设计层面两者的实质都相同,无人机的最优轨迹都满足连续悬停飞行结构。
