基于混沌压缩感知和DNA编码的多图像加密算法
2022-03-30杜鑫昌高瑜翔曹远杰涂雅培吴美霖
杜鑫昌,高瑜翔,曹远杰,涂雅培,吴美霖
(成都信息工程大学 通信工程学院(微电子学院),四川 成都 610225)
0 引言
随着互联网技术的快速发展,5G技术开始逐渐进行商用。人们进行信息交换的媒介也在发生着巨大的变化,从最初的文本信息逐渐过渡到图像信息和视频信息,从而使信息传递过程中所占据的信道带宽与信息占据的存储空间也越来越大[1]。另外,随着人们越来越频繁地进行信息交流,如何保证信息的安全性也是所面临的重要问题[2-3]。
传统的加密算法已不再适用于加密数据量大、冗余度高和相关性强的数字图像信息[4-5]。20世纪70年代发展起来的混沌理论为加密算法提供了新的方向,混沌系统的初值与参数极端敏感性、非周期性和长期演化轨道的不可预测性与图像加密系统的密钥敏感性、密文呈噪声特性和明文敏感性等特性相对应,因此基于混沌系统的密码产生算法在图像加密中的应用受到了极大的关注[6]。低维混沌系统虽运行速度快、运行效率高,但系统初始值少,密钥空间较小、安全性能较低。高维混沌系统虽然安全性能较高,但由于系统较复杂,故运行效率低[7]。因此,为改善加密方案的性能,需要与其他的加密算法相结合。
DNA编码技术是密码学与生物技术相结合的新型研究领域。DNA序列不仅组合规则多样,而且还存在着较高的并行性以及信息存储密度高等优点[8-9]。因此将DNA编码技术与混沌加密系统相结合能够有效地改善加密方案的性能。压缩感知(Compressed Sensing,CS)[10-11]作为一种新的信号采集方法,在远低于奈奎斯特采样频率的情况下,可以从采样过程中精确地重建原始信号[12]。对比传统的采样方法,压缩感知在相同采样值的情况下可以恢复更多的信息。近几年来,基于压缩感知的图像加密方案的研究是图像加密领域的研究热点之一。
为此,本文提出了一种基于混沌压缩感知与DNA 编码的多图像加密算法。通过混沌方程产生的伪随机序列,构建压缩感知受控测量矩阵及DNA运算规则序列,同时对多幅加密图像进行压缩加密并合并为一幅密文图像,在保证信息安全性的前提下,极大地增加了带宽利用率,节省了存储空间。所以,基于混沌压缩感知与DNA编码图像加密技术具有很好的应用前景。
1 基础知识
1.1 压缩感知
压缩感知是一种新兴的信息获取与处理理论,最早由文献[12]提出。在远低于奈奎斯特采样频率的情况下,从采样样本中精确地重建原始信号。
压缩感知的核心思想主要包括3个方面:
(1) 信号的稀疏表示
通常信号都是在时域或者空域中来表示,也可以在其他变换域中通过一些少量元素的组合来近似地表示该信号。信号的稀疏表示是压缩感知理论的先验条件,压缩感知采集处理的信号必须是稀疏的。常见的信号稀疏基包括正(余)弦基、小波基以及chirplet基等[13]。
本文提出的加密方案中采用小波基对图像做稀疏处理,小波图像将图像信号转化为高频和低频部分,最低频的部分给出了图像的一个粗略尺度近似,然而高频成分填充了图像的细节部分。以标准测试图像Lena作为测试图像,如图1所示,稀疏图像中图像的绝大部分信息分布在左上角部分,其余部分的像素值灰度值几乎为零。不同剪切率下的稀疏图像的重建图像的峰值信噪比(PSNR)如表1所示。由表1可知,选择性地舍去黑色部分的区域对于信号重构的质量影响不大。因此,将多幅不同的密文稀疏图像剪切合并为一幅稀疏图像,就可以达到多图像合并压缩的效果,如图2所示。

(a)剪切率为0

(b)剪切率为0.5

(c)剪切率为0.75

表1 不同剪切率下重构图像质量分析

(a)合并2幅图像

(b)合并4幅图像
(2) 编码测量(采样过程)
测量矩阵影响了信号采样压缩复原的效果。测量矩阵包括确定性测量矩阵和随机测量矩阵。随机矩阵中的高斯矩阵和伯努利矩阵都能够满足约束等距条件(RIP)。
RIP定义:定义测量矩阵A的RIP参数δk为满足式(1)的最小值δk[10]:
(1)
式中,x为K稀疏信号。若δk<1,则称测量矩阵A满足K阶RIP[10]。
但是,随机矩阵的不确定性和传输存储过程中占据较大的空间等缺点,难以在实际运用中使用。确定性测量矩阵可以很好地克服这些不足,因此很多研究学者利用其他技术在构造受控的测量矩阵,例如Dimakis,Smarandache和Vontobel利用LDPC校验矩阵来构建测量矩阵;刘鑫吉、夏树涛采用阵列码构造测量矩阵;LeiYum,Jean Pierre Barbot采用混沌序列构造测量矩阵[14]。
(3) 恢复算法(非线性)
压缩感知的重构问题的求解是一个非凸优化问题,属于NP难问题。由低维M维的矢量求解高维N维的矢量,是一个欠定问题的求解。常见的压缩感知恢复算法包括:匹配追踪算法、正交匹配追踪算法、分段正交匹配追踪算法和压缩采样匹配追踪算法等来重构原始信号[13]。
1.2 混沌映射
1.2.1 超混沌Lorenz系统
超混沌Lorenz系统是Lorenz混沌系统的一种演变。主要定义如下:
(2)
当a=-10,b=8/3,c=28且-1.52≤r≤-0.06时,系统处于超混沌状态。
1.2.2 Chen氏超混沌系统
陈氏混沌系统与Lorenz系统相似,但不拓扑等价而且更加复杂。定义如下:
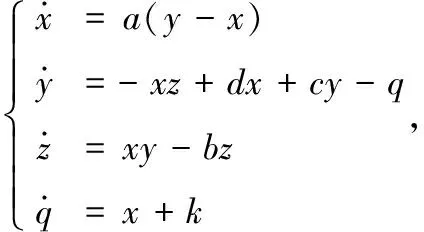
(3)
式中,a,b,c,d,k是系统参数,a=36,b=3,c=28,d=16,-0.7≤k≤0.7。Chen系统进入超混沌系统,可以生成4条混沌序列。
1.3 DNA基本理论
在生物学中,每条DNA分子链包含4种核酸碱基:A,C,G,T。其中,碱基A与碱基T互补,碱基C与碱基G互补[15]。通过规定A,C,G,T分别编码为00,01,10,11,这样的编码方案有24种,但是只有8种编码方案满足Watson-Crick规则[15],如表2所示。

表2 DNA编码方案
对应于8种DNA编码规则,也分别存在8种加法、减法以及异或运算规则。任何一个碱基在每行每列都是唯一的,即序列的运算结果也是唯一的。表3,表4和表5分别介绍了DNA编码的运算方案。
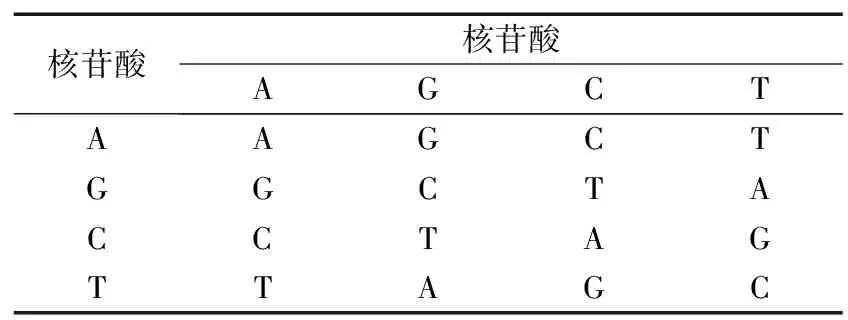
表3 DNA加法运算方案
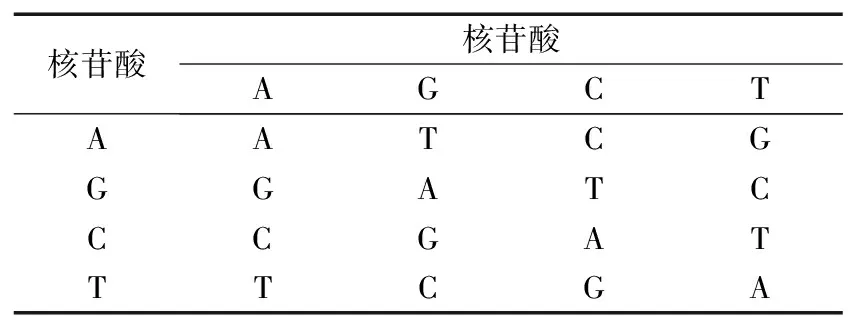
表4 DNA减法运算方案

表5 DNA异或运算方案
1.4 安全散列算法
安全散列算法是一个密码散列函数家族,包括SHA-1,SHA-224,SHA-256,SHA-384和SHA-512。本文采用SHA-256哈希函数用于图像加密系统混沌系统初始值的生成,通过把消息或数据压缩成摘要,使得数据量变小,将数据的格式固定之后打乱混合,重新创建一个散列值的指纹。对于任意长度的数据,SHA-256都会产生一个256 bit的二进制哈希值,任何一个输入数据的改变,都会使生成的哈希值发生很大的改变,所以SHA-256具有较高的安全性[16]。本文通过随机选取一幅图像数据作为哈希函数的输入,然后将生成的256 bit二进制密钥分为8块的十六进制字符串,表示为:
H=(h1,h2,h3,h4,h5,h6,h7,h8)。
(4)
加密系统中超混沌Lorenze混沌系统的初始值r为:
(5)
2 总体加密方案
总体加密方案如图3所示,输入加密图像通过SHA-256函数生成系统密钥,通过密钥计算生成加密系统中混沌系统的初值并生成多个伪随机序列。将多幅加密图像进行稀疏基稀疏变换得到加密图像的小波稀疏图像。截取每幅加密图像小波图的左上角部分拼接为一整幅小波图。为降低稀疏图像中非零元素点的相关性,使之分布的更加均匀,对稀疏图像进行加权置乱处理。利用超混沌Lorenz系统方程生成伪随机序列构造受控的测量矩阵并进行压缩感知测量得到压缩加密后密文图像,通过Chen氏超混沌系统生成的伪随机序列构造DNA矩阵并生成DNA编解码运算序列。与密文图像进行分块DNA操作,获得最后的密文图像。

图3 总体加密方案设计Fig.3 Overall encryption scheme design
3 加密与解密步骤
3.1 加密步骤
(1) 将需加密的图像经过稀疏基稀疏处理得到稀疏图像,截取每幅小波图像的右上角非零信息部分将其合并为一幅稀疏图像。
(2) 对稀疏图像进行加权置乱操作,通过提高稀疏信号之间的差异性,降低相邻非零元素的相关性,从而提高重建信号的重构质量。
(3) 加密图像通过SHA-256函数生成系统中多个混沌系统的初始值,通过不同的初始值使混沌系统迭代生成多条伪随机序列用于后续操作。
(4) 利用超混沌Lorenz系统产生的伪随机序列构造受控测量矩阵,并将压缩感知线性测量后得到的压缩加密后的密文图像进行无重复置乱操作,降低相邻元素的相关性。
(5) 利用Chen氏超混沌系统产生的伪随机序列构建DNA矩阵,并构建DNA编码规则序列、DNA运算规则序列以及DNA解码序列。
(6) 将密文矩阵与DNA矩阵进行分块处理,进行块与块之间的编码、运算和解码操作,最后合并为密文图像。
3.2 解密步骤
解密过程就是加密过程的逆过程:
(1) 将密文图像与DNA矩阵分块后进行解码、运算和编码的逆操作生成密文矩阵P1。
(2) 对密文矩阵P1进行置乱逆操作获得观测矩阵P2。
(3) 通过重建算法对观测矩阵进行信号重构获得密文图像P3。
(4) 对密文图像P3进行加权置乱逆操作得到小波图像P4。
(5) 对小波图像P4进行分割获得各个加密图像的小波图像并进行小波逆变换得到加密图像。
4 仿真实验
4.1 压缩性能分析
为验证本文算法压缩复原的性能,选取多幅标准的灰度测试图像作为实验图像。在压缩率分别为0.75和0.5的情况下通过比较PSNR来衡量本文算法的压缩性能。
加密单幅图像的第1组和第2组测试如图4和图5所示。

(a) 明文图像

(b) 压缩率0.75密文图像

(c) 压缩率0.5密文图像

(d) 压缩率0.75复原图像

(e) 压缩率0.5复原图像

(a) 明文图像

(b) 压缩率0.75密文图像

(c) 压缩率0.5密文图像

(d) 压缩率0.75复原图像

(e) 压缩率0.5复原图像
加密2幅图像如图6所示。

(a) 明文图像

(b) 明文图像Camera

(c) 压缩率0.75密文图像

(d) 压缩率0.75复原图像Lena

(e) 压缩率0.75复原图像Camera

(f) 压缩率0.5密文图像

(g) 压缩率0.5复原图像Lena

(h) 压缩率0.5复原图像Camera
加密4幅图像如图7所示。

(a) 明文图像

(b) 压缩率0.75密文图像

(c) 压缩率0.75复原图像

(d) 压缩率0.5密文图像

(e) 压缩率0.5复原图像
加密压缩单幅图像重构图像质量分析如表6所示。合并压缩2张图像下重构图像质量分析如表7所示。合并压缩4张图像下重构图像质量分析如表8所示。
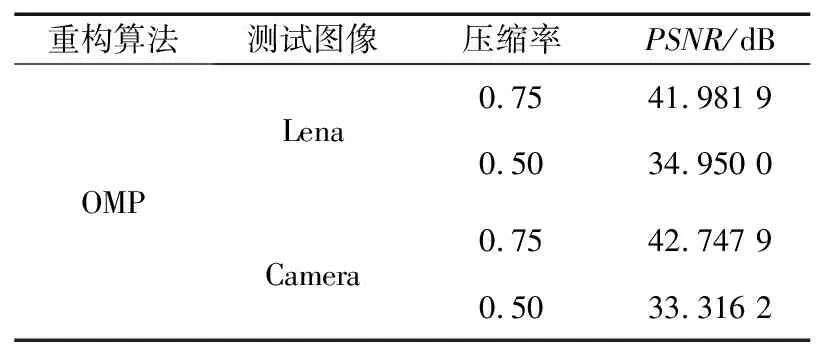
表6 加密压缩单幅图像重构图像质量分析

表7 合并压缩2张图像下重构图像质量分析

表8 合并压缩4张图像下重构图像质量分析
经过多次多组实验仿真分析,本文提出的压缩加密算法具有良好的性能,在合并压缩2张图像情况下,复原图像与原图像相比,图像的质量基本不受影响。存储空间节省率达到75%。在合并压缩4张图像的情况下,复原图像与原图像相比,复原图像虽然在重构质量上有一定的影响,但是在视觉上影响不大,还是可以清晰地观察到图像的细节,存储空间节省率达到87.5%。
4.2 密钥空间
密钥空间是指能够生成密钥的所有可能密钥的集合。决定了密码系统的最重要的特性之一,理论上图像加密算法的密钥空间大于2100就可以抵御蛮力攻击[17]。本文加密算法的密钥由3部分组成:
(1) 给定的超混沌Lorenz系统的初始值a,b,c以及r。
(2) 一图一密,随机选取一幅加密图像通过函数SHA-256生成的256 bit的哈希值。
(3) 给定的Chen氏超混沌映射的系统初值X0,Y0,Z0,H0。
超混沌Lorenz混沌方程中,a∈(-40,40),b∈(-40,40),z∈(1,81),r∈(-250,250),x、y和z的步长为10-13,r的步长为10-12,因此混沌方程的密钥空间大小约为7.68×1059。SHA-256的密钥空间为2128,Chen氏超混沌系统具有5个系统初值(如果计算进度为10-14,密钥空间为4×1056)。故加密算法总的密钥空间远远大于2100[17],所以该方案的密钥空间足够抵御蛮力攻击。
4.3 敏感性分析
敏感性的性能分析有2个参数:像素变化率(NPCR)和统一平均变化强度(UACI)。2个参数分别表示了明文图像与加密图像之间的像素值变化率和平均变化强度值[20]。它们的理想值分别为:NPCR=99.609 4%,UACI=33.463 5%。如果2幅图像所有相应位置的像素值均不相同,则NPCR=100%,即:
(6)
(7)
敏感性分析如表9所示。

表9 敏感性分析
由表9可知,密文图像与各个明文图像在敏感性的参数上接近于理论值,表明本文提出的加密算法是安全的。
4.4 统计分析
针对统计规律的攻击方案被称为统计分析攻击。统计分析攻击是指攻击者通过分析密文与明文的统计规律来破译密码。通过截获的密文图像的统计规律并与明文的统计规律进行比较,从而分析出明文图像与密文图像之间的变换关系。统计分析包括直方图分析和相邻像素点的相关性分析。
4.4.1 直方图分析
为抵御统计分析,密文的直方图必须是均匀的,并且完全不同于明文图像的直方图。以合并加密4幅图像为例,如图8所示。

(a) 明文图像Lena直方图
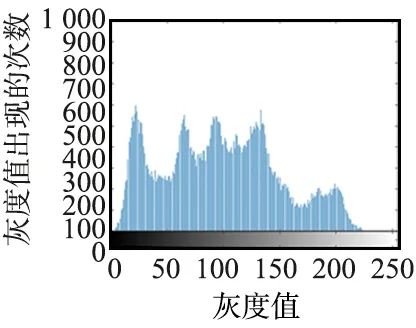
(b) 明文图像Peppers直方图

(c) 明文图像Couple直方图

(d) 明文图像Boat直方图

(e) 合并密文图像直方图图8 实验图像直方图Fig.8 Experimental image histogram
由图8可知,密文图像的像素分布的直方图是均匀分布,且不同于任何一个明文图像的直方图,因此可以抵抗统计直方图攻击。
4.4.2 相邻像素相关性分析
相关性分析如表10所示,是指对2个或多个具备相关性的变量元素进行分析,从而衡量变量之间的相关密切程度。由于图像的相邻像素之间存在着较高的相关性,通过一个像素往往会泄露周边像素的信息。因此攻击者往往可以通过图像的这一特性推测出周围像素的灰度值,从而对密文图像进行破解。所以为了抵御统计攻击,需要打破这一特性。下面从像素的垂直方向、对角线方向以及水平方向对密文图像进行分析,计算表达式为:
(8)
(9)
(10)

(11)
由表10可知,密文图像的各个方向像素值之间的相关性的数值极大地接近于零,因此可以抵抗基于相关性的统计攻击能力。
4.5 信息熵分析
信息熵是反映图像信息不确定性的重要指标。信息熵的值越大,表明图像信息的不确定性越大。信息量越大,说明信息的可视性就越小,系统的加密性能就越好。就以灰度等级为256的图像而言,信息熵的理论最大值为8[21]。一般来说,密文图像的信息熵超过了7.99,就说明该加密系统具有良好的加密性能。因此对加密前后的密文图像与各个明文图像的信息熵进行比较。信息熵分析如表1所示。
信息熵的计算公式为:
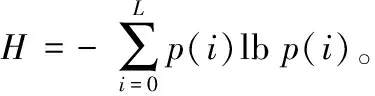

(12)
由表11可知,密文图像的信息熵数值接近于信息熵的理论最大值,说明本文提出的算法具有良好的加密性能。
5 结束语
本文提出的基于混沌压缩感知与DNA编码多图像加密算法,利用压缩感知技术与混沌理论、DNA编码技术及其他加密算法相结合,同时对多幅图像进行压缩加密,在保证了密文图像传递的安全性的同时极大地减少了传递过程中密文的带宽占用率并节省了存储空间。加入SHA-256安全散列算法,一次一密,极大地增加了整体加密算法的安全性。与其他类似加密算法相比较,本文提出的算法具有一定的优势。由于在压缩感知理论中不同的稀疏基、测量矩阵和重构算法都会对重构信号的质量造成影响,因此下一步将对此方面进行优化,提高重构信号的质量。
