提速货物列车车轮凹磨限值研究

彭敬康，崔大宾，付耀东，雷鹏程，李立

(西南交通大学机械工程学院，四川 成都 610031)

随着城际间商品贸易往来日益发展，铁路运输已成为货物运输的主要运输方式之一，在国民经济中具有重要地位[1]，可以说铁路运输效率直接影响着经济发展速率。目前我国货物列车平均运营速度仅50 km/h[2]，低速运营的货车线路亟待提高运行速度以提升运输效率，但列车提速的前提是解决提速带来的诸多动力学及轮轨磨耗问题。区别于传统机械系统，轨道列车系统具有一种高度非线性的轮轨接触关系，当列车提速后，较大的轮轨间作用力极易产生轮轨磨耗[3]。轮轨磨耗会改变初始的轮轨接触特性，直接影响列车的运行状态。车轮凹磨作为列车车轮磨耗的一种主要形式，是影响列车提速性能的关键原因之一。严重的车轮凹磨将对列车的运行性能造成不利影响，甚至威胁行车安全[4]。目前国内外学者针对车轮踏面凹磨及列车(车辆)动力学性能问题进行了相关研究。SAWLEY 等[5]通过对某型货车车轮运行状况进行跟踪测试，分析了车轮凹磨现象的形成过程，并基于凹磨车轮与钢轨的不良接触状态探讨了车辆的动力学行为，车轮凹磨将引起车辆动力学性能下降。FRÖHLING 等[6]从力学角度入手，通过研究车轮凹磨与轮轨接触状态的关系证明了凹磨将增大轮轨作用力，对轮轨接触力学特性不利。MACE 等[7]对车轮凹磨状态下的车辆曲线通过性能进行了分析，结果表明，车轮踏面凹磨会降低车辆曲线通过性能。CUI 等[8]研究了踏面凹磨对动车组系统动力学的综合影响，并提出了高速动车组的车轮镟修阈值。孙宇等[9]探讨了车轮踏面凹磨对轮轨相互作用的影响。车轮磨耗一直都是影响列车运行性能的主要问题[10−11]，凹磨作为车轮磨耗的主要形式，应引起铁路部门的高度重视，及时进行镟修可保证列车正常运行。但在实际运营中，由于对运营成本的考虑，车轮踏面允许存在一定程度的凹磨，而我国至今并未制定货物列车车轮凹磨维修标准。为保证货物列车提速运行的安全性及稳定性，对提速货物列车车轮凹磨镟修限值研究显得尤为重要。本文以车轮凹陷值为研究对象，基于实测车轮磨耗数据及车辆参数，建立了货物列车系统动力学模型，分析了不同凹陷值下的车轮踏面对提速货物列车的动力学性能影响，最后根据分析结果给出了提速货物列车的车轮凹磨镟修限值。

1 轮轨接触状态分析

图1为车轮凹磨示意图，将车轮凹磨程度以凹陷值[5]进行定义。图2 中A点为车轮踏面外侧最高点，B点为整个踏面的最低点，A和B2 点间的垂向距离H即为车轮凹陷值。

图1 车轮凹磨Fig.1 Hollow-worn of wheel

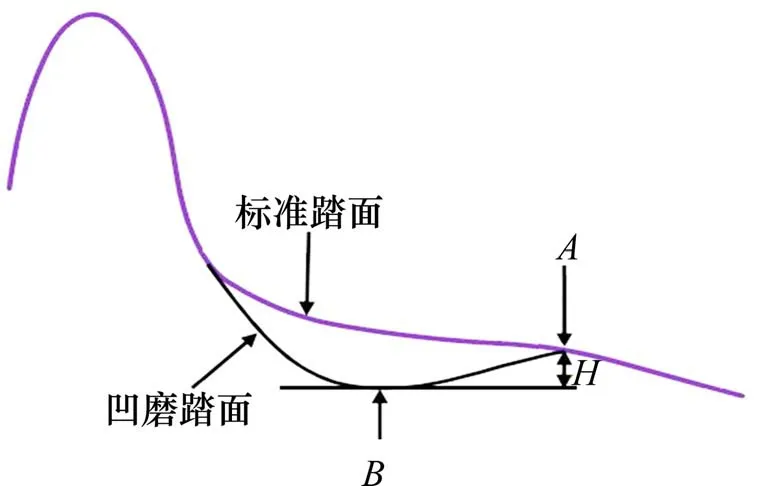
图2 车轮凹陷值Fig.2 Depression value of wheel

对阜淮线某型提速货物列车车轮磨耗进行了跟踪测试，基于不同运营时期的磨耗车轮数据获得了7 种不同凹陷值下的车轮踏面廓形，如图3 所示。由图3可见，踏面凹磨区域主要分布在名义圆左右30 mm 范围内，凹磨中心位于在名义滚动圆附近。

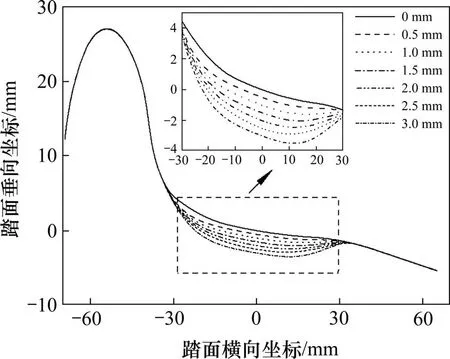
图3 车轮踏面廓形Fig.3 Profiles of wheel tread

将不同凹陷程度踏面与CN60(60 kg/m)钢轨进行匹配，探讨凹磨对轮轨接触状态的影响，图4给出了凹磨车轮与CN60 钢轨匹配时的轮轨接触点对分布。可见当车轮未发生磨耗时，车轮与钢轨在名义圆附近匹配良好，轮轨接触点分布均匀。当车轮产生凹磨现象后，车轮与钢轨的接触点开始向凹磨区域两侧移动，并随着凹陷值逐渐增大，轮轨接触点向凹磨区域两侧集中的现象越明显，接触点左右横向间隔也逐渐加宽。当车轮凹陷值达到3.0 mm 时，车轮与钢轨在名义圆附近几乎无法形成有效接触，此时轮轨接触点将随着列车运行在凹磨区域两侧发生跳跃，使轮轨产生冲击、碰撞，降低列车的运行性能。此现象也被称为假轮缘效应[4]。

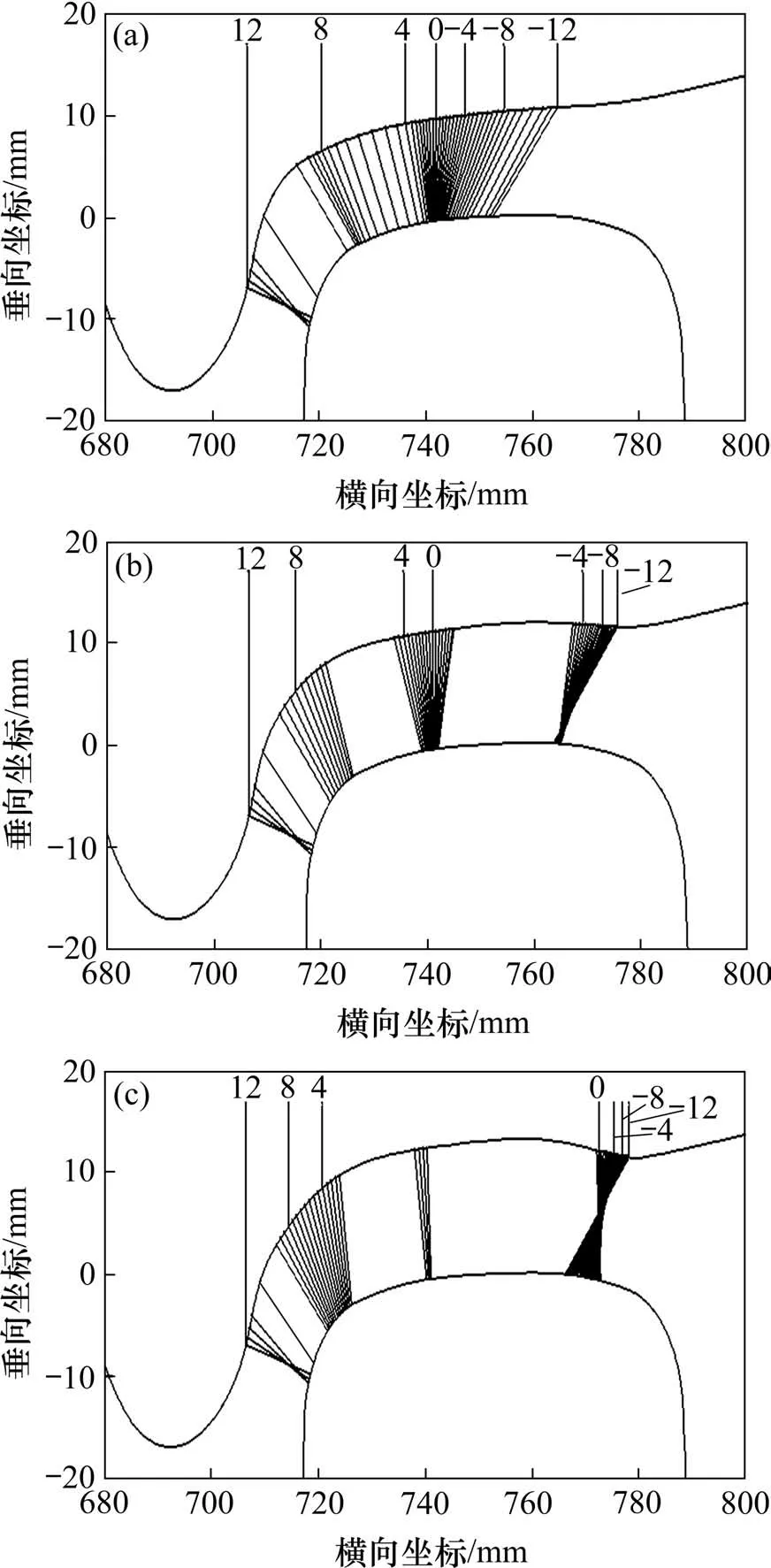
图4 轮轨接触几何Fig.4 Contact geometry of wheel-rail

等效锥度用于评价轮轨接触特性，在工程中常作为列车间接动力学性能衡量指标[12]，其计算公式为：

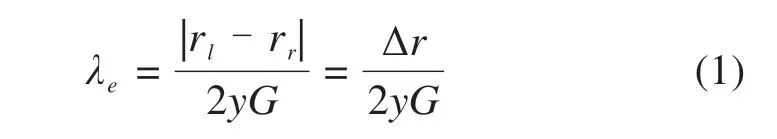
式中：rl，rr分别为左右车轮名义滚动圆半径；Δr为轮对滚动圆半径差；yG为轮对横移量。

UIC 519 将轮对横移幅值为3 mm 处的等效锥度规定为名义等效锥度，图5给出了不同凹陷值下的车轮等效锥度随轮对横移量的变化曲线。可见，标准车轮的名义等效锥度约为0.1，当凹陷值逐渐增大，车轮名义等效锥度也随之增大，当凹陷值达到3 mm 时，车轮名义等效锥度已增至0.24，是标准车轮踏面的2.4 倍。车轮等效锥度的增大势必引起较大的轮轨作用力，使轮对横向晃动进一步恶化。

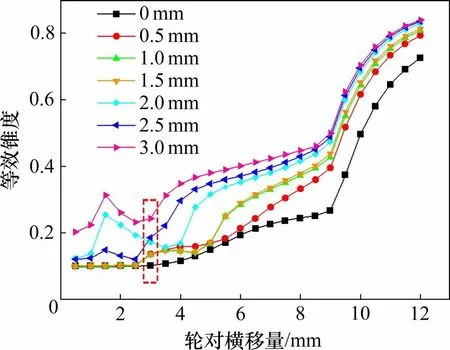
图5 等效锥度Fig.5 Equivalent conicity

2 列车动力学性能分析

2.1 列车系统动力学模型建立

基于阜淮线某型货物列车实测车辆参数，设置轨距1 435 mm，轮对内侧距1 353 mm，轨底坡1/40，运用Simpack 多刚体动力学软件[13]建立列车系统动力学模型。图6所示为列车单节车辆结构拓扑图。

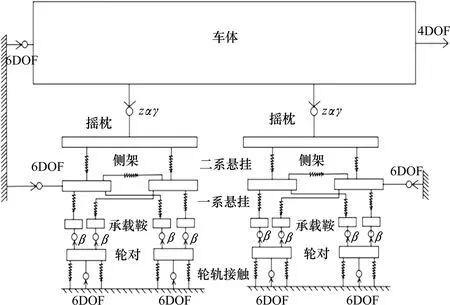
图6 列车车辆结构拓扑图Fig.6 Topological diagram of train structure

图3已给出不同凹陷值下的凹磨踏面廓形，为探究踏面凹陷值对列车系统动力学性能的影响，利用凹磨踏面数据建立Simpack轮对模型作为系统的输入变量。同时，考虑到Simpack动力学软件对系统自由度的计算限制，列车模型以3节车辆编组来反映头车、中间车和尾车的动力学特性。由于阜淮线属于我国繁忙铁路干线，为保证线路日常运营，并未对阜淮线进行轨道不平顺激励测量。但调查得知，我国干线铁路轨道不平顺性处于美国五级、六级铁路之间[14]，考虑阜淮线较差的线路状态，因此设置美国五级谱作为线路不平顺激励。直线线路设置长度800 m，采样频率200 Hz。曲线线路采用相同的采样频率，设置半径R700 m，圆曲线700 m，超高100 mm，两端缓和曲线100 m，前直线600 m，后直线200 m。

2.2 直线运行性能分析

蛇行失稳临界速度是用于评价列车直线运行稳定性的一种关键指标，目前对货物列车的一种非线性临界速度计算方法——单次积分法[15]可以描述为：首先让列车以某一速度通过一段施加了随机不平顺激励的线路，使列车系统受到足够的振动激励，之后列车进入一段无激励的平直轨道，观察列车导向轮对的运动状态，一般认为当导向轮对的运动状态由发散变为稳定，且在下一通过速度下导向轮对不再稳定，此速度即为列车的非线性临界速度。图7 以装载LM 标准型面车轮为例，当列车以142 km/h 速度通过一段激励线路后进入理想平直线路，其导向轮对运动状态由不稳定逐渐趋于稳定，而列车以143 km/h 的速度通过相同线路时，其轮对运行状态呈发散状态，因此列车的非线性临界速度为142 km/h。

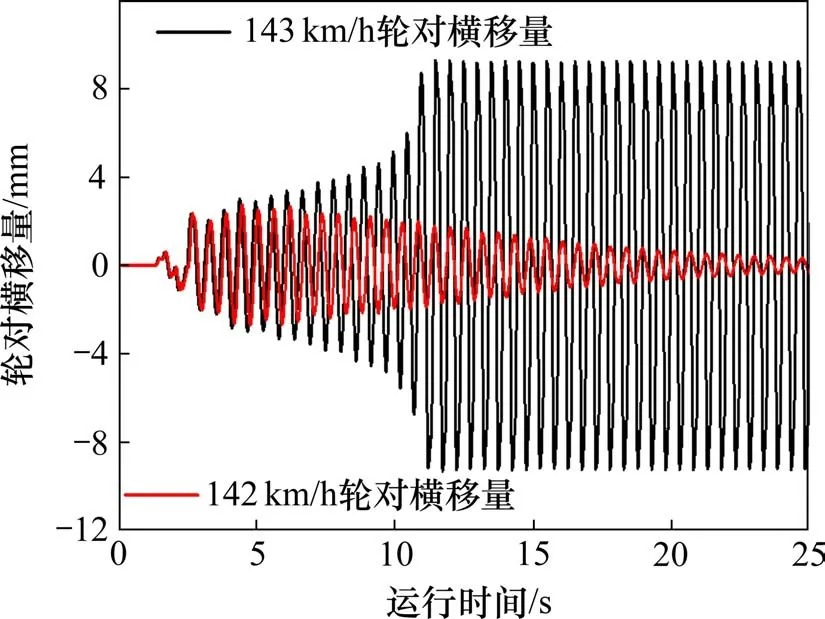
图7 LM踏面临界速度Fig.7 Critical speed of LM tread

按上述计算方法将不同凹陷程度的磨耗车轮临界速度计算如图8所示，可见随着踏面凹陷值增大，列车的非线性临界速度将由142 km/h 逐渐减小至107 km/h。经调查，该型货物列车的转向架构造速度为120 km/h，当凹陷值达到3.0 mm 后，列车的临界速度已低于转向架构造速度，这将造成列车在提速通过直线区段时极易发生蛇形失稳现象。

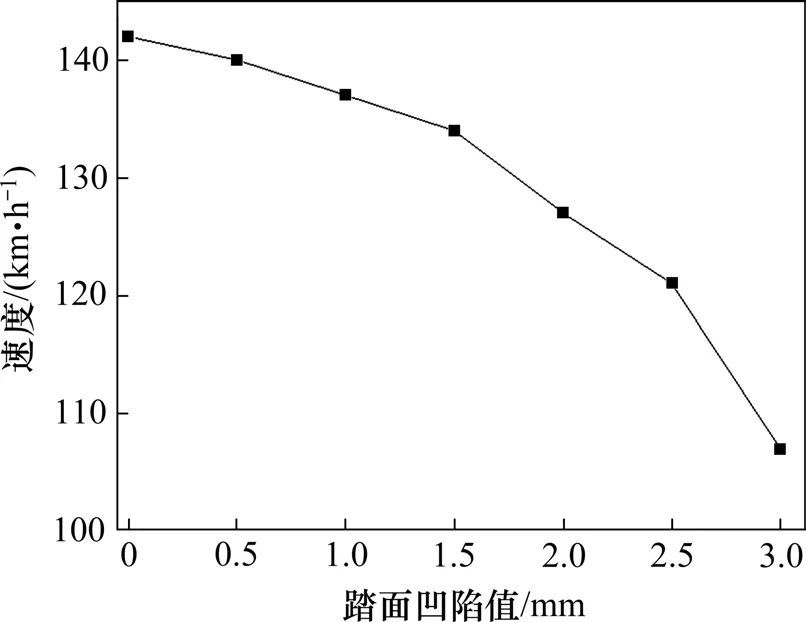
图8 凹磨踏面临界速度Fig.8 Critical speed of hollow-worn tread

列车运营速度受到如线路构造速度、车辆构造速度和机车最高运营速度等诸多因素影响。尽管列车在直线区段可以较高速度通过，但由于曲线、道岔、车站和坡度的制约，列车的运营速度仍处于较低等级，提升列车的运营速度是提速的主要目标。经调查，我国多数普速货物列车运营线路与阜淮线具有相似特征，受线路构造速度和复杂路段限速影响，列车很难以较高的运营速度通过线路。目前对阜淮线提出的运营速度提速目标为80 km/h，在80 km/h 速度下对车轮凹磨限值进行研究对保证列车正常运行具有实际意义。

轮对横向振动加速度是列车稳定性的重要评价指标，我国GB/T 5599—2019 尚未给出轮对横向加速度的相关评价指标，因此，采用UIC518 规定的轮对横向加速度均方根值判定准则：sÿ|lim=5 m/s2。其中加速度均方根计算公式为：

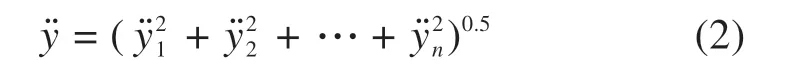
式中：ÿ1,ÿ2,…,ÿn为采样区段内各采样点的轮对横向振动加速度值；ÿ为该采样段轮对横向振动加速度均方根值。

图9 按式(2)分别计算了80 km/h 工况下各凹磨踏面轮对横向加速度均方根值。由图9可见，踏面凹陷值在0～1.5 mm 范围内对轮对横向加速度影响不大，当凹陷值增大至2.0 mm 后，轮对横向加速度明显增大，当凹陷值增大至3.0 mm 时，部分加速度均方根值接近容许限值。

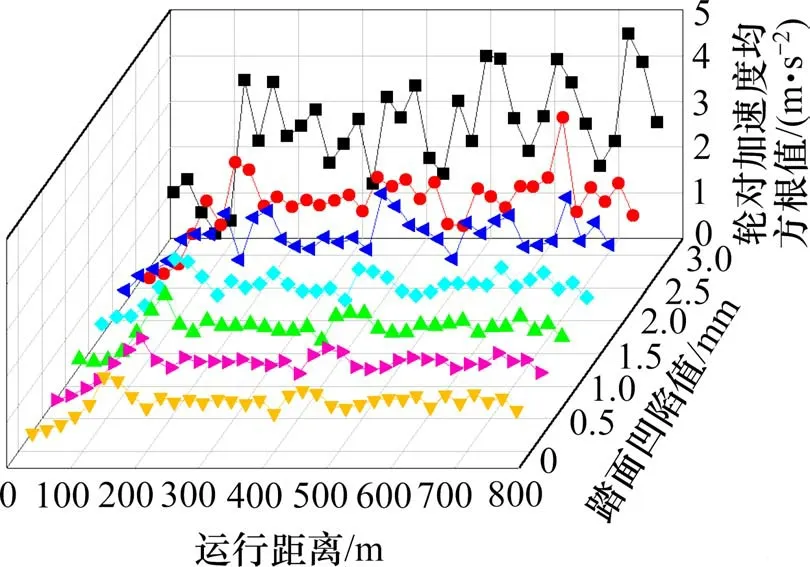
图9 轮对横向加速度均方根值Fig.9 RMS of lateral acceleration of wheelset

在现场试验中，工务部门对7种不同凹陷值的凹磨车轮各选用3 辆试验列车在80 km/h 运营速度下进行轮对横向加速度测试，记录每辆试验列车在试验区段内的轮对横向加速度最大值，最后计算3辆试验列车的轮对最大加速度平均值。为对理论计算结果进行验证，将理论计算结果按上述方法进行相同处理，取理论轮对横向加速度最大值均值与试验结果对比如图10 所示。可见，理论结果与现场试验具有相同的变化趋势，轮对横向加速度随踏面凹陷值增大而增大，且数值较为吻合。

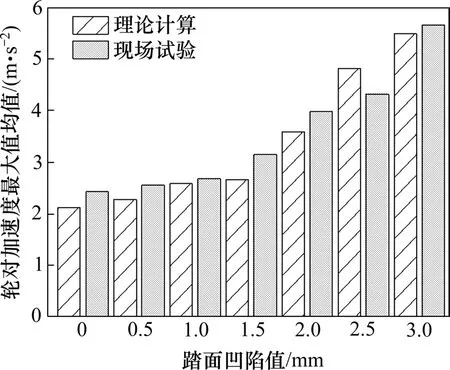
图10 理论/试验轮对横向加速度对比Fig.10 Comparison of the oretical/experimental lateral acceleration of wheelset

采用GB/T 5599—2019 规定的货车转向架横向稳定性指标对稳定性进行评价：对侧架横向振动加速度数据进行0.5～10 Hz带通滤波处理，对滤波后的时域振动波形进行评估，若波形中存在连续6次超过8 m/s2的现象，判定转向架失稳。将装有不同凹陷值的踏面的侧架横向加速度滤波处理如图11所示。凹陷值在0～1.5 mm范围内侧架横向加速度增长不显著，凹陷值超过2.0 mm 后侧架加速度出现大幅增加，当凹陷值达到3.0 mm 时，部分侧架横向加速度值已超过8 m/s2，但并未连续6 次超过。

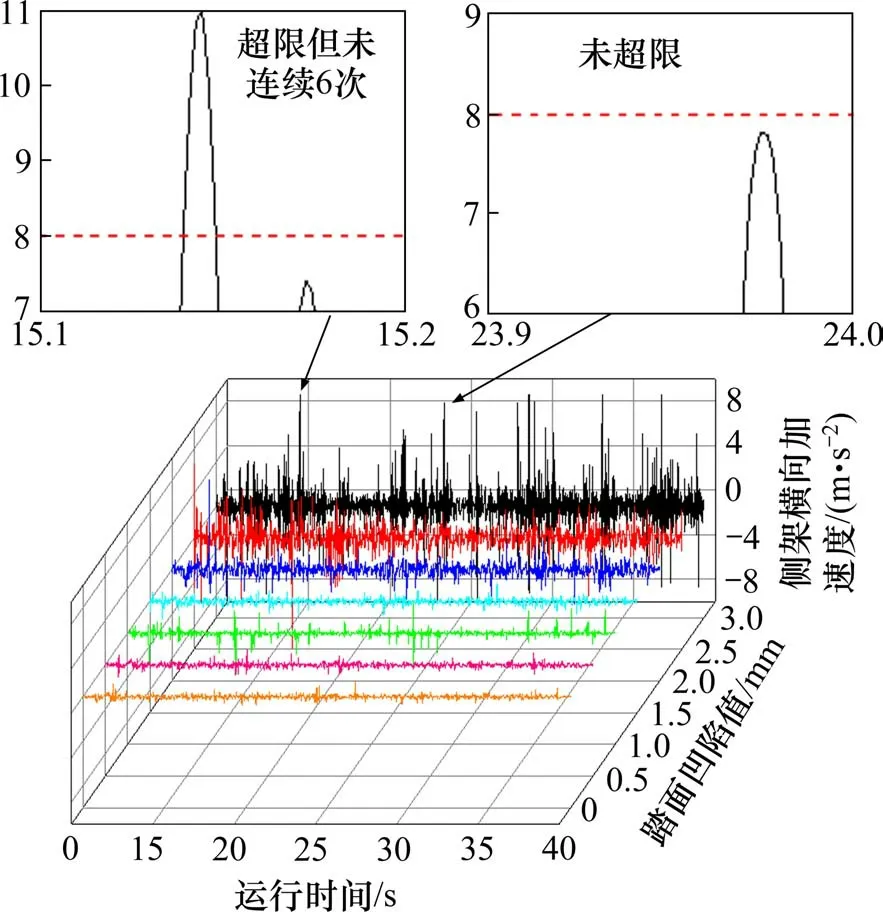
图11 侧架横向加速度Fig.11 Lateral acceleration of side frame

为研究车轮凹磨对列车系统振动频率的影响，将轮对及侧架横向振动加速度频谱分析结果对比如图12和图13所示。由图12可见，当踏面凹陷值处于0～2.5 mm 范围内时，轮对横向振动主频集中在0～10 Hz 范围内，振动幅值随凹陷值的增大呈上升趋势。当踏面凹陷值达到3.0 mm 时，凹磨激发了80～90 Hz 范围内的强烈振动，且轮对横向振动幅值显著增加。图13 所示的构架横向振动频谱规律与图12 类似。调查发现，导致这一现象的原因是车轮凹磨引起的剧烈轮轨冲击振动由轴箱传递至侧架[16]，激发了侧架横向刚体模态振动所致。

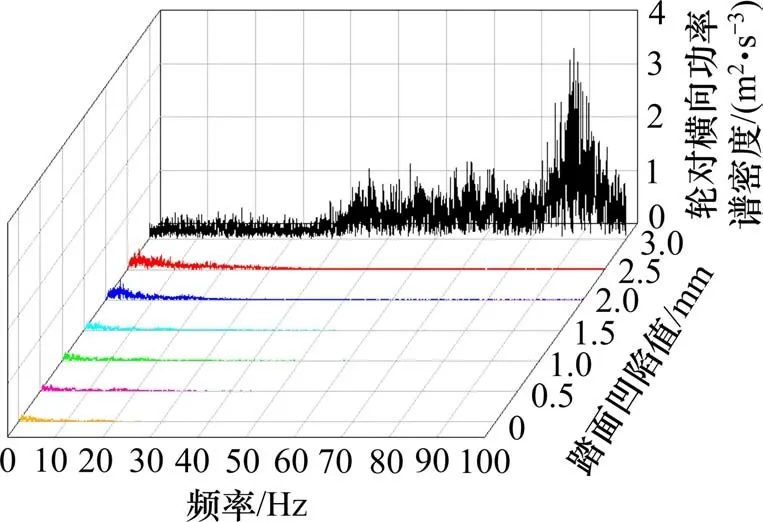
图12 轮对横向振动加速度频谱分析Fig.12 Spectrum of lateral vibration acceleration of wheelset

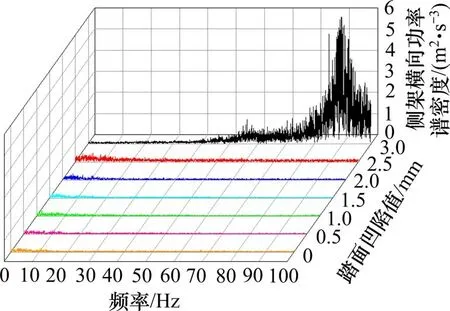
图13 侧架横向振动加速度频谱分析Fig.13 Spectrum of lateral vibration acceleration of frame

图14 给出了列车运行过程中踏面凹陷值分别为0，2.5 和3.0 mm 的轮轨运行接触轨迹。由图14可见，标准踏面在列车运行过程中，与钢轨匹配特性良好，轮对在一定范围内发生较小横移，轮轨接触点未出现跳跃现象；当踏面凹陷值达到2.5 mm 时，轮轨在凹磨区域内不能有效接触，轮轨接触点在凹磨区域两侧发生跳动，引起一定程度的轮轨冲击，加剧了轮对、侧架的横向振动；当凹陷值达到3.0 mm 时，轮轨接触点在凹磨区域两侧横向跳动距离明显增大，造成严重的轮轨冲击现象，这是引发侧架剧烈横向晃动的原因。

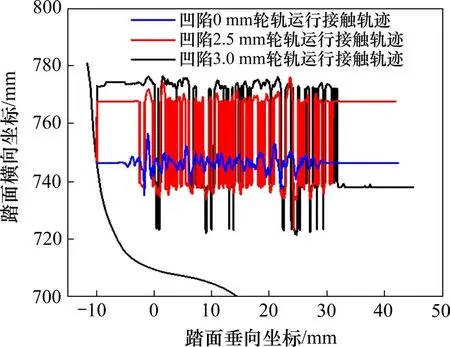
图14 轮轨运行接触轨迹Fig.14 Trace of wheel-rail contact point

我国采用GB/T 5599—2019 规定的平稳性指标对列车的运行平稳性进行评价，平稳性指标的公式为：

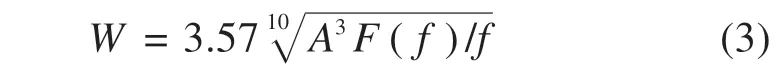
式中：W为列车平稳性指标；A为车体横向加速度，m/s2；f为车体振动频率；F(f)为与f相关的加权系数。

对列车系统加速度时域响应特性作FFT 变换可获得加速度频率响应函数，此时对各频段进行横向平稳性指数计算，采用下式算得全频段横向总平稳性指数：

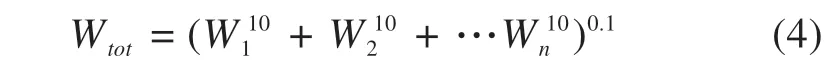
理论计算和现场试验皆采用上述方法对不同凹陷程度的踏面对应的列车运行平稳性进行计算，其中现场试验给出了列车运行平稳性的最大值、最小值和平均值。将计算结果对比如图15 所示，可见理论计算和现场试验的结果都表明列车的横向平稳性指数将随踏面凹陷值增长而增大，当凹陷值由2.0 mm 增长至3.0 mm 时，列车平稳性指标增长较明显。尽管因理论模型的简化使平稳性理论计算结果与现场试验存在一定偏差，但从结果来看，理论计算与现场试验具有相同的变化趋势，理论计算结果处于现场试验的平稳性指标范围内，并与试验平均值具有较高的一致性。这也进一步验证了理论模型的准确性。GB/T 5599—2019 规定货物列车运行平稳性指数不高于3.5 时，认为列车运行品质为优。尽管踏面凹陷值的增长使列车运行平稳性有所降低，但计算范围内的踏面凹陷值均能满足列车平稳性要求。

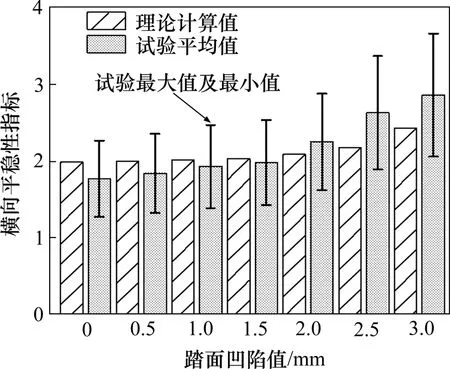
图15 理论/试验横向平稳性指标对比Fig.15 Comparison of theoretical/experimental lateral ride index

2.3 曲线通过性能分析

图16 给出了曲线通过时的列车轮对横向加速度均方根值，当车轮凹陷值由0 mm 增大至1.5 mm时，轮对横向加速度均方根值以较小幅度发生增长，当凹陷值由2.0 mm 增大至3.0 mm 时，轮对横向加速度增长明显，且在3.0 mm 凹陷值下部分加速度值已超出限值。

对列车曲线通过时的侧架横向振动加速度进行0.5～10 Hz 带通滤波处理，结果如图17 所示，当踏面凹陷值在2.0 mm 以下时，侧架横向加速度以较低幅度增长，当凹陷值由2.0 mm 增长至3.0 mm 时，侧架横向加速度增长幅度较明显。同时观察到，当凹陷值达到3.0 mm 时，侧架横向加速度已存在连续6 次峰值超过8 m/s2的现象，此时判定侧架发生失稳。

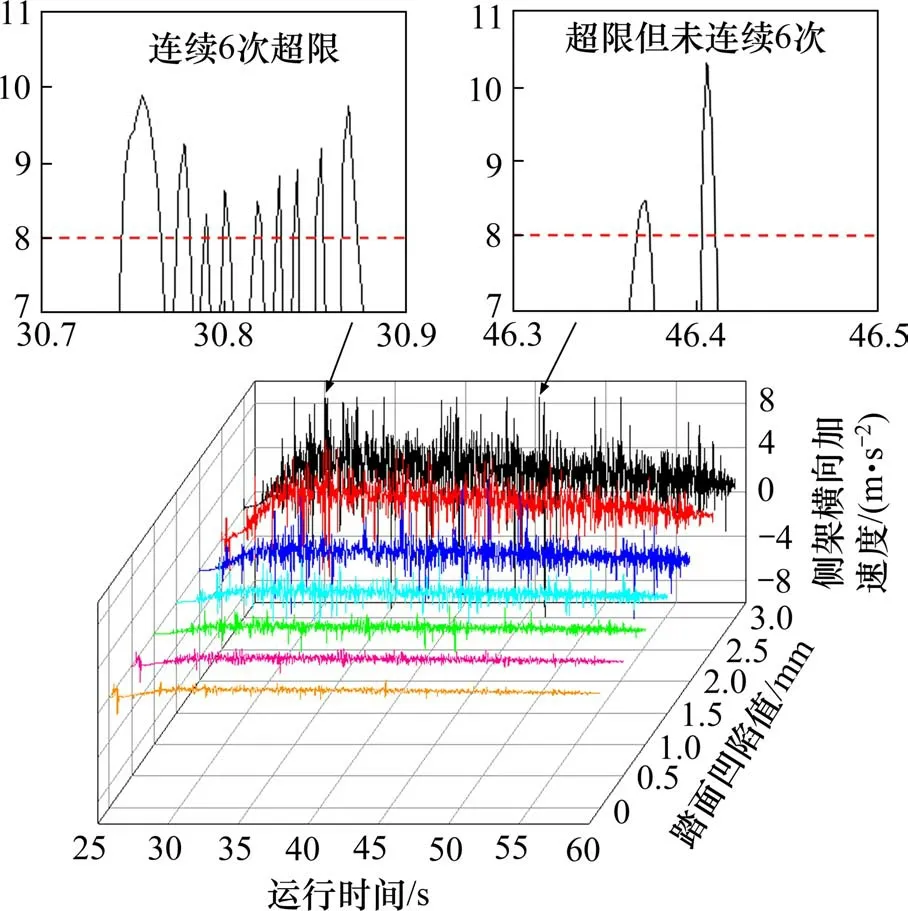
图17 曲线通过侧架横向加速度Fig.17 Lateral acceleration of side frame in curve

脱轨系数用于鉴定列车是否会因轮轨横向力的作用而逐渐爬上轨头脱轨，GB/T 5599—2019 对货物列车脱轨系数作出如下规定：当轮轨横向作用力Q的作用时间大于0.05 s 时，其脱轨系数(Q/P) ≤1.0。将列车通过曲线的脱轨系数计算如图18 所示，尽管踏面凹陷值的增加会引起脱轨系数产生一定程度变化，但数值间的差距并不大，因此踏面凹陷值的增长对脱轨系数的影响较小。

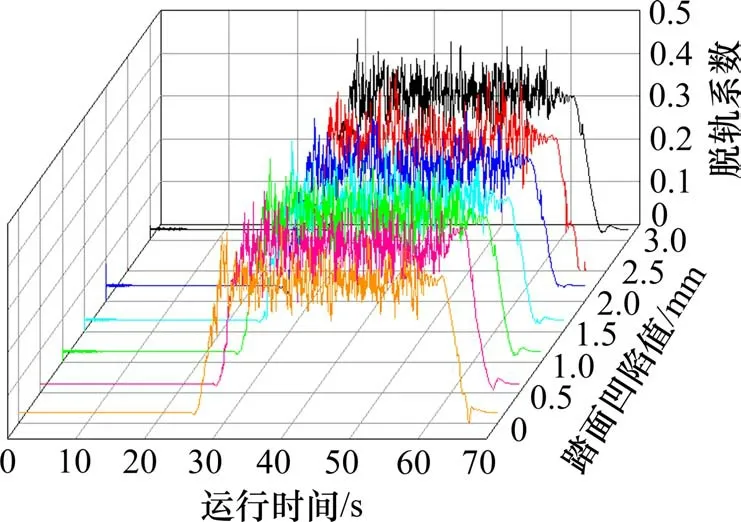
图18 脱轨系数Fig.18 Derailment coefficient

轮重减载率用于评定车辆是否会因一侧车轮减载过大而导致列车倾覆，我国对货物列车轮重减载率的容许限值为：(ΔP/P) ≤0.65，其中ΔP为轮重减载量，P为平均轮重。将不同凹陷值下的车轮曲线通过轮重减载率对比如图19 所示，可见随凹陷值的增大，轮重减载率呈增大趋势，踏面凹陷3.0 mm 下的轮重减载率因轮轨冲击出现瞬时增大并接近容许限值。

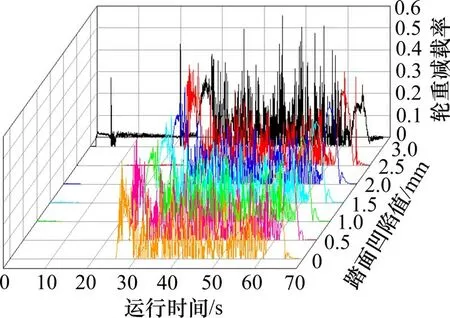
图19 轮重减载率Fig.19 Rate of wheel load reduction

3 结论

1) 对阜淮线上某型提速货物列车车轮磨耗进行跟踪测试，基于不同运营里程的磨耗车轮获得了7种凹陷值下的车轮踏面廓形。通过对比轮轨接触几何特性，发现凹磨踏面在名义圆附近不易与钢轨形成有效接触，导致轮轨接触点在此范围内发生横向跳动，且跳动距离随着车轮凹陷值增大而增加。同时，踏面凹陷值的增加会增大踏面等效锥度，对列车动力学性能产生不利影响。

2)根据货物列车实际参数，运用Simpack多刚体动力学软件搭建了列车系统动力学模型，分析了踏面凹陷值对提速货物列车系统动力学性能的影响，并将理论结果与现场试验结果对照，验证了理论模型的准确性。计算结果表明踏面凹陷值的增大会降低列车的临界速度，引起轮轨间冲击振动，加剧轮对与侧架的横向振动，降低列车运行平稳性。车轮凹磨对脱轨系数影响不大，但会增加曲线运行时的轮重减载率并造成列车运行失稳。

3) 通过对比车轮凹陷值与列车系统动力学性能指标容许限值可知，当踏面凹陷值在2.0 mm 以内时，凹磨对列车动力学性能影响不大，当凹陷值达到2.5 mm 时，列车的各项动力学性能指标出现显著恶化，当凹陷值达到3.0 mm 时，列车的动力学性能已出现较大程度降低，部分指标已超出容许值。因此，建议运营速度提升至80 km/h 的货物列车车轮凹陷值应控制在2.5 mm 内，以保证列车提速后的安全运营。