温度与振动耦合作用下青藏铁路路基沉降可靠性分析

2022-03-30余雨薇陈卫雄郭继林李林唐家银

铁道科学与工程学报 2022年2期

余雨薇，陈卫雄，郭继林，李林，唐家银

(1. 西南交通大学数学学院，四川成都 611756；2. 中铁十二局集团铁路养护工程有限公司，西藏拉萨 250014)

青藏铁路是世界上海拔最高与线路最长的高原铁路，而多年冻土区路基工程在青藏铁路全程的占比极高。长期工程实践表明，青藏铁路成败的关键在路基，路基的关键在冻土，冻土的关键在融沉[1]。当路基融沉、振陷等沉降变形超过一定阈值时，将对轨道平整度产生严重的负面影响，甚至引起轨道破坏，进而影响铁路运营安全。随着铁路运输的迅猛发展，国内外学者对铁路路基变形现象展开了大量的理论和实况研究。关于影响路基融沉变化的因素研究中[2−8]，主要有气温、路基土类型、含水率和压实度等。列车运行荷载引起的路基土动力反应问题也得到了关注。MONISMITH 等[9]研究了重复荷载作用对黏性路基土永久变形的影响，提出了累积塑性应变的表达式，得到广泛应用，为后续研究打下了坚实基础。李德武等[10]把机车和车辆简化成不同的力学模型，得到了列车竖向振动荷载的数定表达式。WANG等[11]采用蒙特卡罗(MC)方法计算了全球变暖条件下冻土路基的不确定沉降行为。结合路基可靠度评估内容，马立峰等[12]运用层次分析法和模糊数学理论确定了冻土区路基稳定状况的模糊综合评价模型。徐东升[13]以路基融沉变形10 cm 为阈值，运用响应面法计算了青藏铁路修建完成后长达50 a的路基可靠度指标。苗姜龙等[14]基于BP 神经网络法进行冻土路基变形可靠度预测。纵观国内外文献，对于冻土工程影响因素的研究主要集中在严格控制岩土动力学、冻土土质特性、路基土含水量变化等方面的实验室数据，缺少以实际监测数据为分析源动力，对路基变形预测和控制的理论研究和工程运用技术。尤其对于温度、列车运营振动应力2个因素如何在耦合作用机制下，定量影响多年冻土路基沉降变形的探究更为鲜见。本文基于青藏铁路实际工况监测到的自2010 年起10 a 内的路基高度数据，开展青藏铁路多年冻土场地路基变形规律的数据统计分析研究，建立了多元回归模型，给出青藏铁路冻土区路基高度变形值定量的经验回归方程。并在此基础上完成变形预测和路基可靠性评价工作，为后期铁路养护部门及时采取保护措施、维修与治理提供理论支持依据，具有重要的理论与工程意义。

1 多变量路基变形值分析模型

1.1 多变量影响的回归分析基础

回归分析研究的主要对象是客观事物变量间的统计关系，它是建立在对客观事物进行大量试验和观察的基础上，用来寻找隐藏在那些看上去是不确定的现象中的统计规律性的统计方法[15]。

随机变量Y与一般变量X1,X2,…,Xp的线性回归模型为：

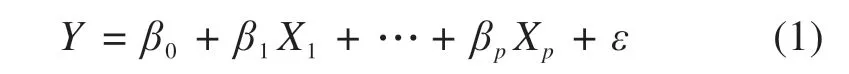
式中：β0,β1,…,βP是p+ 1 个未知参数，ε为不可观测的随机误差项，假定ε∼N(0,σ2)，p≥2 时，称式(1)为多元线性回归模型。设Y与X1,X2,…,Xp的n组观测数据为(Yi;Xi1,…,Xip)(i= 1,2,…,n)，称为样本，则模型(1)的样本形式为：

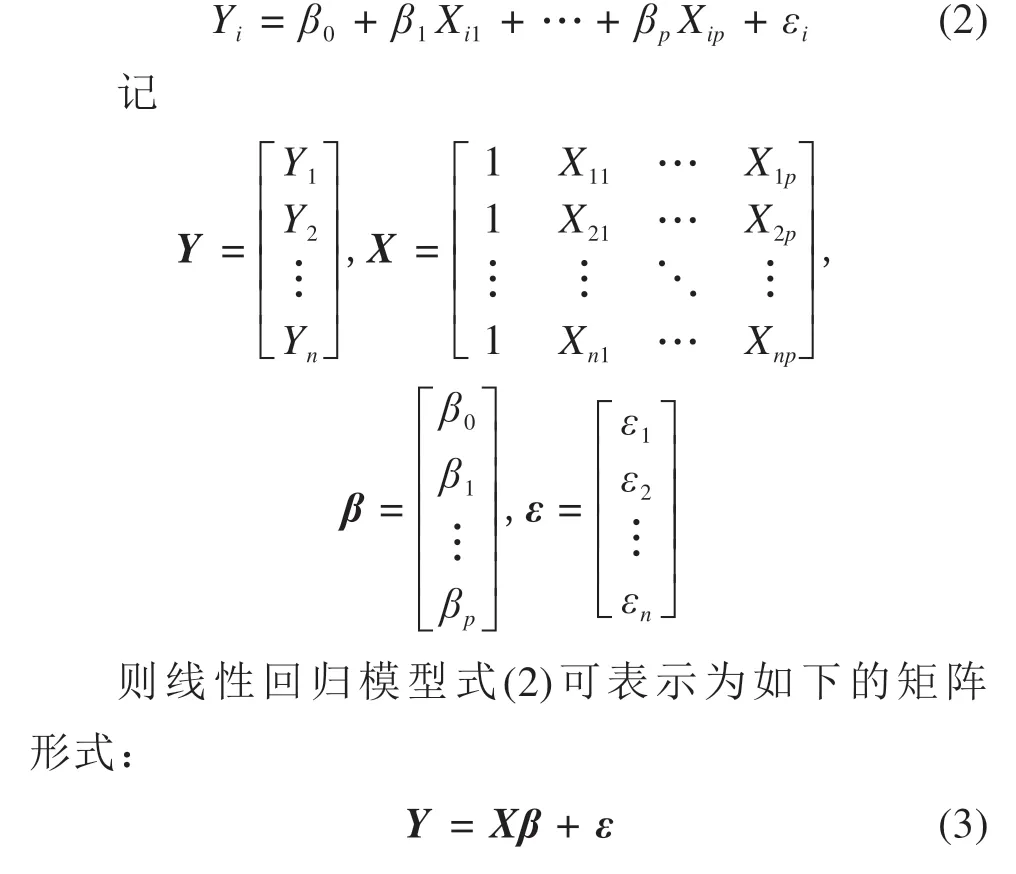
其中：ε∼N(0,σ2In)。

1.2 温度-振动耦合作用下的路基变形值预测模型

探究路基沉降变形规律，以路基高度差值为因变量Y，环境温度、行车振动应力、时间、路基类型为内生控制变量(X1,X2,X3,X4)，可用多元线性回归模型拟合，满足如下关系：

为经验回归方程，得到环境温度和振动耦合作用将如何影响青藏铁路多年冻土地区路基沉降变形的定量方程式，基于此，可进一步做出未来时间青藏铁路路基高度沉降数值的预测分析。

2 温度-振动耦合作用下路基沉降可靠性模型

2.1 路基沉降变形预测值的分布

2.2 既定失效阈值下的路基沉降可靠性评估

由于路基较稳定地呈现沉降变形，所以路基高度变形差值和变形值阈值均为负值，当未来时刻路基沉降预测值Ŷi小于变形值阈值时，认为路基沉降过大，危害到行车安全。根据高原地区行车安全规范设计的路基变形值阈值为y*，计算未来时刻路基沉降预测值Ŷi大于等于变形值阈值y*的概率，便可完成对未来时刻青藏铁路多年冻土地区行车安全可靠度计算：

2.3 随机失效阈值下的路基沉降可靠性评估

实际工程中，因影响青藏铁路路基变形值的参数(如温度、动荷载)均为随机变量，造成路基不同地段的差异；以及不同工况条件如路基土含水量、压实度的差异等诸多因素，均可导致路基沉降阈值亦为一随机变量Y*，具有不确定性。从而路基变形值与随机失效阈值Y*之间的可靠性计算模型更具普适性。

3 青藏铁路某测点路基沉降变形分析算例

基于青藏铁路沿线K1496+700 测量点左侧的数据进行算例分析，其路基类型为骨架护坡、一般路基，获取了2010年至2019年共10年间每月共117 组路基高度及对应的外界气温数据，部分样本数据如表1所示。

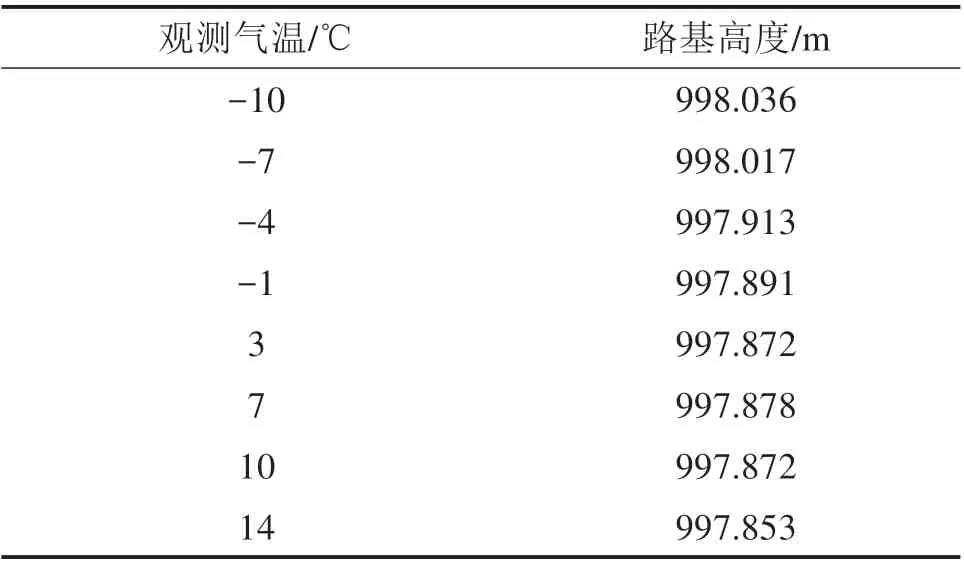
表1 K1496+700处的部分样本观测数据Table 1 Observation data of some samples at K1496+700

3.1 数据预处理

3.1.1 列车振动应力的量化

中国铁道科学研究院集团有限公司分别在其环形试验基地和广深准高速铁路上进行了实测，然后利用计算机进行动力有限元分析，最后提出高速铁路路基设计动应力幅值计算式[16]：

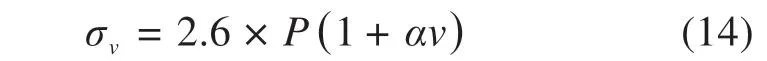
式中：σv为路基设计动应力幅值，kPa；P为机车车辆的静轴重，t；α为速度影响系数，高速、无缝线路α= 0.003，准高速、无缝线路α= 0.004；v为列车运行速度，速度在300 km/h 以内时以实际速度计，超过300 km/h时，按300 km/h计。

考虑到工况中青藏铁路沿途运行速度和线路设计，选取α= 0.004，用高速铁路路基设计动应力幅值来衡量行车振动应力，即：

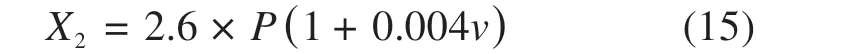
3.1.2 行车振动应力均匀试验设计

均匀试验设计(Uniform Design Experimenta‐tion)选用路基动应力幅值作为试验指标，选取青藏铁路运营时列车轴重和行车速度中上限和下限之间的12个水平，试验方案如表2。

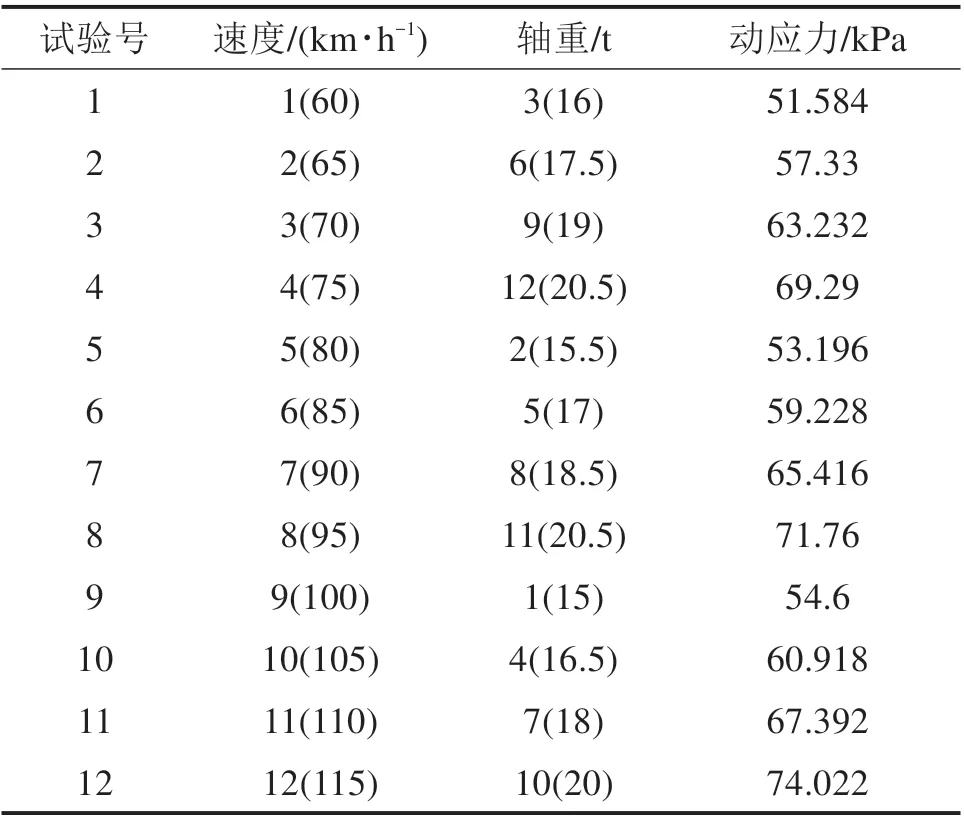
表2 均匀设计试验方案及结果Table 2 Test scheme and results of uniform design

路基表面的应力冬季逐渐增大，在春季和夏季逐渐减小，在秋季逐渐增大。这种现象是冬季地面结冰，路基表面刚性增加，形成刚性壳。同样，夏季熔融深度最深，路基表面刚度最小。因此，路基表面冻结温度越低，刚度越大，路基表面应力越大[17]。

3.2 K1496+700左侧测量点路基沉降可靠性分析

通过对散点图的观测与多次试验和经验总结，发现对变量X2进行对数变换X͂2= lnX2，得到线性回归分析结果的拟合效果更好。由于K1496+700左侧测量点路基类型为骨架护坡、一般路基已确定，于是考虑简化模型。基于变换后的数据和简化模型，得到相应线性回归模型参数最小二乘估计值，以及回归方程的显著性检验结果，如表3所示。

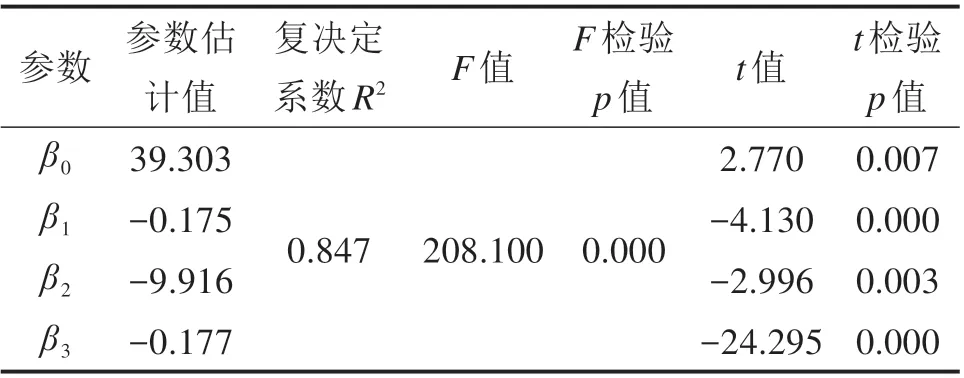
表3 路基变形多元回归模型求解结果Table 3 Multivariate regression model solution results of subgrade deformation

表3显示了由最小二乘法计算得到的模型各未知参数估计值β̂0,β̂1,β̂2,β̂3的取值，根据模型建立的多元线性经验回归方程为：

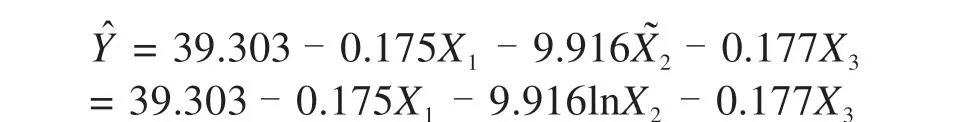
式中：X1为外界气温，℃；X2为铁路路基设计动应力幅值，kPa；X3为时间，月，以2010 年1 月为时间起点；Y为路基高度差值，mm；Y=Yi-Y0，Yi为距离时间起点第i个月的路基高度。

通过经验方程得知，路基高度的沉降变形与环境温度的变化、行车振动应力和时间呈负相关。其他影响因素不变，当温度为负温时发生冻胀现象，当温度为正温时发生融沉现象；列车速度加快、轴重增加会导致行车振动应力值加大，产生路基振陷现象；且随着时间的进展，路基高度存在累积变形，路基沉降越来越严重。回归结论与实际情况相符。

回归方程的显著性检验结果分析，由表3，拟合优度检验计算复决定系数R2= 0.847，表明回归拟合的效果显著；对于F检验其p值以及t检验的p值，均小于0.05 的显著性水平，表明整体上回归方程显著以及每一个内生变量都是显著的。以上3种检验结果都表明对于路基高度变形值拟合的多元回归方程是高度显著的。

残差是实际观测值与通过回归方程给出的回归值之差，进一步对回归做残差分析。由图1 知，标准化残差散点分布大致在一条直线上，因此可认为关于模型误差项的正态性假定是合理的，进一步验证了多元线性回归经验方程对现有监控数据拟合效果优良。

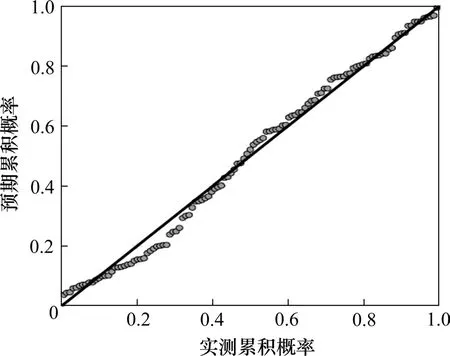
图1 回归标准化残差的正态P-P图Fig.1 Normal P-P plot of regression standardized residuals

由于随机失效阈值更具有普适性，假设随机失效阈值服从正态分布，均值为阈值自身，方差一般相对较小[18]，且通过过去10 年下降的幅值变化及根据现场维护专家的推算确定，Y*∼N(-100,0.3)。据统计国内外13条线路的实测数据，距离路基面约0.5～0.7 m 处，动应力衰减约40%左右[19]。取路基表面动应力均值68.72 kPa，引入动应力衰减系数0.6，计算得路基内部动应力值41.23 kPa，该测点在未来时间X3= 500(2051 年8 月)，温度X1= 12，振动X2= 41.23，根据式(13)计算路基沉降100 mm的可靠度值：

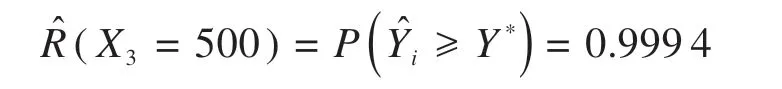
当要求青藏铁路路基可靠度大于等于0.999 4时，应该在2051 年8 月前对路基进行检修，为工程实际操作提供重要的指导意见。

图2反映了当其他影响因素固定，只有单一因素影响时，随时间的推移青藏铁路路基可靠度预测变化。可靠度随时间逐渐降低，对于实例所固定的变量值，X3≤450 时，路基可靠度都近似为1，为更直观清晰呈现可靠度下降趋势，从第450个月开始绘图。其中图2(a)表明温度越高，路基沉降越严重，同一时刻对应的路基可靠度越小。图2(b)表明振动应力越大，路基沉降变形越大，同一时刻对应的可靠度越小。图2(c)表明随机失效阈值的均值越小，同一时刻对应的行车安全可靠度就越小。图2(d)表明随机失效阈值方差的改变对青藏铁路路基可靠度影响不大，但失效阈值方差越大，路基可靠度随时间下降得越缓慢。

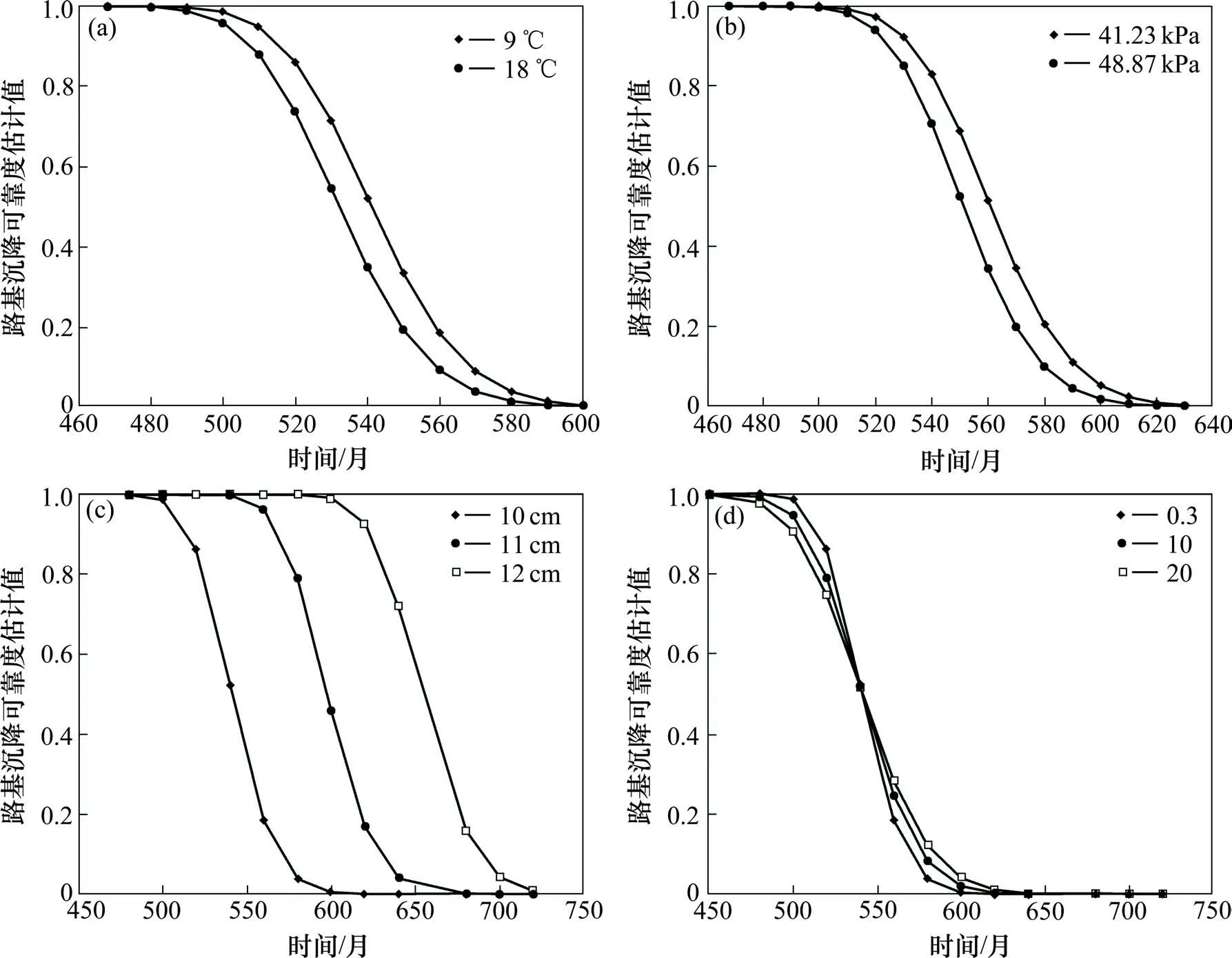
图2 不同条件下青藏铁路路基可靠度Fig.2 Reliability of Qinghai-Tibet Railway subgrade under different conditions

联系多元非线性回归以及实例中计算温度对路基沉降可靠度的分析结果，为控制温度对路基沉降的不良影响，路基保障应采取主动降温或保温的措施，增强地基土的冻结能力，抬升人为上限，改善地表条件，消除地基多年冻土退化所产生的融化下沉。考虑到实际工况，不同的措施需要分别在冬季和夏季完成。阻水保温、冬病夏治(土护道、片石保温护坡、排水明沟和回填积水坑措施)、夏病冬防(保温盲沟和热棒措施)的措施需高效结合。伴随列车行进过程中产生的振动应力对路基产生的不良振陷影响，在发生路基病害严重时，可适当对放行列车采取减速减重措施。