固定交通检测器布设对快速路交通流量预测影响的实证研究

2022-03-30董春肖张立涛孙洪运张军张昕冉

铁道科学与工程学报 2022年2期

董春肖，张立涛，孙洪运，张军，张昕冉

(山东理工大学管理学院，山东淄博 255000)

随着智能交通的发展和交通流量的增加，交通检测器和交通流量预测在预防和疏解交通拥堵方面的作用变得越来越重要。高性价比的布设原则寻求用较少的交通检测器的数量获得更实时准确的交通数据。固定交通检测器作为监测设备，可以采集当前监控断面的交通流量、占有率、速度等数据，并用于确定何时何地是否会或已经发生交通拥堵或交通事故。交通流量预测准确度与交通检测器布设和预测算法息息相关。在交通检测器布设方面，HONG 等[1]研究了交通检测器布设位置对道路交通状态估计的影响，利用基于速度数据细胞传输模型和扩展卡尔曼滤波方法，分析了不同布设间距下的交通检测器的交通状态估计精度，从而确定检测器的最佳间距。EISENMAN等[2]进一步研究了交通检测器的布设位置和数量对实时交通网络流量估计和预测的影响。首先假设检测器位置是随机的，比较不同数量的检测器布设方案下路网性能估计和预测结果的差异。研究发现，大流量高速公路路段更需要布设交通检测器，通过随机选择方法获取的误差最小。FUJITO等[3]利用辛辛那提、俄亥俄、亚特兰大以及乔治亚等地方的现场数据研究了检测器布设间距对行程时间数据估计的影响，研究结果表明交通检测器的布设位置对路段拥挤状态的估计精度有着显著的影响。周敬龙等[4]研究了检测器的精度对全感应信号控制的影响，结果表明交通流量的大小会影响检测器的精确度对全感应信号控制的控制效果。罗向龙等[5]针对交通流短期预测未考虑交通检测器配置的不足，提出了一种基于检测器优化选择的短时交通流量预测算法。以预测的均方误差最小为目标函数，通过遗传算法优化选择合适的检测器，以小波神经网络作为预测算法进行短时交通流量预测。目前关于交通检测器布设对交通流量预测的影响还没有一个系统的研究，本文利用某城市快速路交通数据设计一些实验深入研究这种影响关系。研究的问题是：1) 提出一个检测器布设对交通流量预测影响的分析框架；2) 在此基础上，实证分析检测器间距对断面交通流量预测影响的关系；3) 实证分析检测器数量对路段交通流量预测影响的关系。用真实数据综合分析检测器间距和数量比较困难，所以本文分别展开分析。在交通流量预测算法研究方面，神经网络及其变种的算法得到了广泛应用。YI等[6]提出了一种基于TensorFlow的深度学习神经网络模型，用于利用实时交通数据预测交通状态。ZHAO 等[7]将长短期记忆网络(LSTM)用于交通流量预测，取得了很好的效果。朱云霞等[8]引入遗传算法，通过对BP 神经网络权值阈值的优化，构建道路交叉口的交通流量短时预测模型。DAI 等[9]提出了一种去趋势和深度学习的多对多流量预测模型，采用简单平均趋势法进行数据预处理，使用卷积神经网络作为预测模型，基于CNN 的非趋势预测模型训练过程中有更快的收敛速度。HAO 等[10]提出了一种嵌入注意力机制的端到端的深度学习框架，可以同时对一个大型地铁系统的所有站点进行多步预测。何龙庆等[11]引入深度神经网络思想，构建交通流时空状态变量，建立短时交通流量预测模型。李佩钰[12]提出一种基于小波分析与神经网络结合的预测模型，首先对原始采样的交通流数据进行消噪，然后用BP 神经网络模型对短时交通流进行预测。孔繁辉等[13]为了提高BP 神经网络预测精度，基于深度学习理论提出一种深度信念网络(DBN)算法优化传统BP 神经网络预测模型。基于神经网络算法具有较强的学习训练能力，预测精度高的特点，本文选择BP神经网络作为交通流量预测模型，BP神经网络具有较高的自学习、自适应和非线性映射能力，对短时交通流量数据预测有很好的效果。本文充分挖掘交通数据的特征，用某城市快速路网的交通流数据进行实验，借助BP 神经网络短时交通流量预测模型，分别从交通检测器的间距和数量2 个方面实证研究其对交通流量预测的影响。

1 模型构建

1.1 研究流程

交通检测器布设对交通流量预测的影响分析流程，如图1所示。

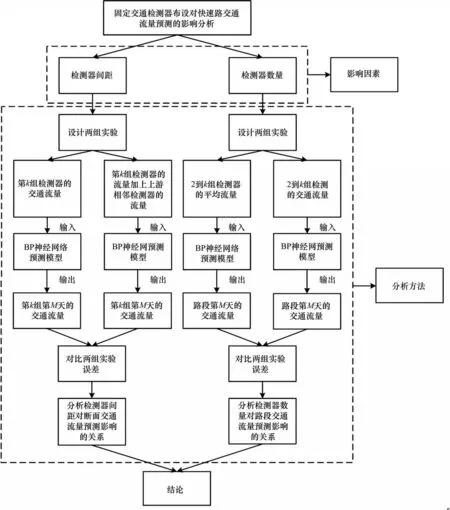
图1 影响分析框架Fig.1 Impact analysis framework

1.2 交通流量预测模型建立

1.2.1 分析检测器的间距对交通流量预测的影响

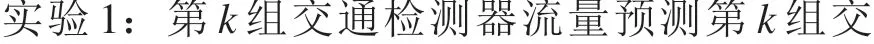
BP 神经网络模型包括输入层，隐含层和输出层，其中relu 为激活函数，MSE 为损失函数，adam 为优化器，迭代次数是200 次。BP 神经网络预测模型如图2和图3所示。

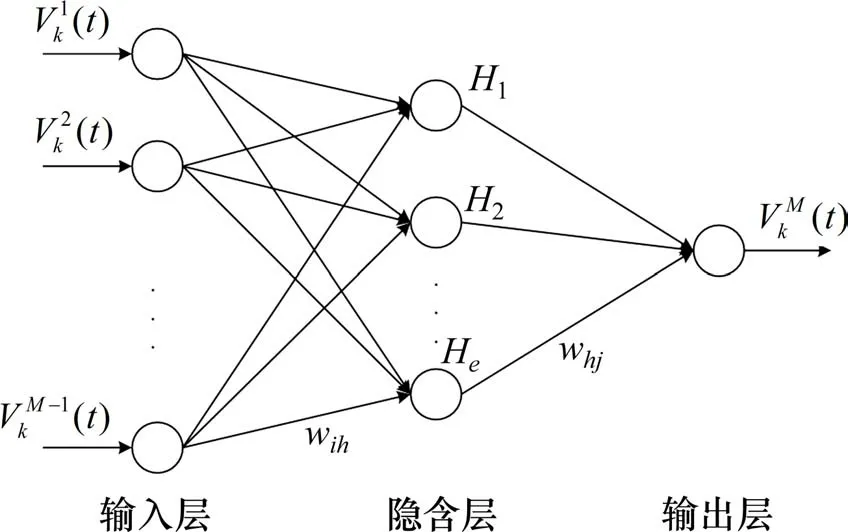
图2 实验1 BP神经网络预测模型Fig.2 Neural network prediction model for Experiment 1

图3 实验2 BP神经网络预测模型Fig.3 Neural network prediction model for Experiment 2

实验1：输入层有17 个神经元，作用函数为relu；隐藏层有15 个神经元，作用函数为relu；输出层有1个神经元，作用函数为linear。

实验2：输入层有35 个神经元，作用函数为relu；隐藏层有30 个神经元，作用函数为relu；输出层有1个神经元，作用函数为linear。

1.2.2 分析检测器的数量对交通流量预测的影响

检测器和路段有包含的关系，重点选择长路段实验。中间的线圈不靠近匝道，精度更高，所以从中间向两端依次选择路段中2～K组检测器分别预测路段的交通流量。

2 实验分析

2.1 实验数据的采集

实验数据来源于某城市快速路环形电磁感应线圈检测器收集到的交通流量数据，时间是2013年10 月1 日～2013 年10 月31 日。根据交通数据分析，选取了18 个工作日高峰时期7:00～9:00 间隔5 min(共24 个时间段)的一个路网区域中8 个路段上20 组线圈的数据。实验1 选择前17 d 为特征，24 个时间段为样本，前16 个时间段为训练集，后8 个时间段为测试集，预测第18 d 的交通流量；实验2选择上游相邻检测器18 d和本检测器前17 d一共35 d 为特征，24 个时间段为样本，前16 个时间段为训练集，后8 个时间段为测试集，预测第18 d的交通流量。选择的路段和线圈检测器如图4所示。

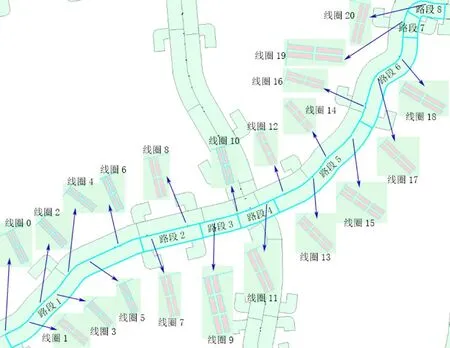
图4 路段和线圈检测器Fig.4 Links and loop detectors

实验选择了8 个路段，均为单向路段，路段3和路段5 为3 车道，其他6 个路段均为2 车道，8 个路段总共7 830 m，一共21 组线圈检测器，平均间距为391.5 m。路段1上游位置有1个出口匝道，路段1 的下游和路段2 的上游位置有1 个出口匝道，路段2的下游和路段3的上游位置有1个入口匝道，路段5的下游和路段6的上游位置有1个出口匝道，路段7的下游和路段8的上游位置有1个出口匝道，路段8 的下游位置有1 个入口匝道。图5 展示了路段1～路段8早高峰18 d平均交通流量。

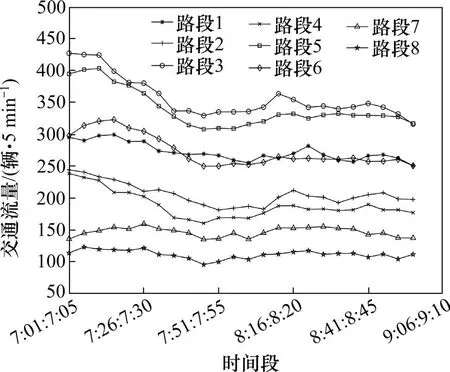
图5 早高峰各路段18 d平均交通流量Fig.5 18 days’ average volume at each link during morning peak

2.2 评价指标

为了评估预测结果的性能，使用2种方法评估预测模型的性能：均方根误差(RMSE)和平均绝对误差(MAE)。均方根误差表示预测值与真实值之间差异的样本标准差，可以说明样本的离散程度，是用来衡量预测值与真实值之间的偏差。平均绝对误差表示预测值和观测值之间绝对误差的平均值，能更好地反映预测值误差的实际情况。

均方根误差(RMSE)的计算公式：

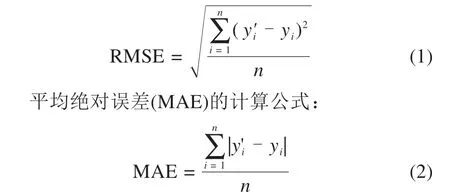
式中：y'i是第i个样本的预测值；yi是第i个样本的真实值；n是样本的个数。

2.3 实证分析

2.3.1 实证分析检测器间距对断面交通流量预测影响的关系

实验1预测结果的均方根误差、平均绝对误差以及实验2 的均方根误差、平均绝对误差，实验2比实验1误差下降率，如表1所示。

表1 实验1和实验2的RMSE和MSETable 1 RMSE and MSE of Experiment 1 and Experiment 2

线圈检测器间距与误差降低率之间的关系(间距从小到大)，如图6所示。通过比较实验1和实验2 的预测结果，20 个线圈检测器实验2 的预测精度高于实验1。说明相邻路段之间的交通流量是有关联的，它们之间会相互影响，但是间距大小与实验2 的预测效果不存在线性相关关系。从图5 可以看出，综合MAE 和RMSE 2 个指标，有4 种结果：1)误差下降率均在30%及以上的对应着3对线圈检测器间距在360～420 m 之间，1 对间距是445 m；2)误差下降率均在20%～30%之间的对应着3 对线圈检测器间距分别是330，417 和480 m；3) 另外也存在着一些2种误差下降率分别存在不同下降区间的特殊情况，但存在一个误差下降率在20%以上，如在间距424，428 和431 m；4) 误差下降率均在20%及以下的对应着6 对线圈检测器间距在250～330 m 之间，2 对间距在510～530 m 之间，1对间距是465 m。合并前3 种结果，取最长的不中断线圈间距是330～450 m，该范围为流量预测场景下线圈布设提供参考。

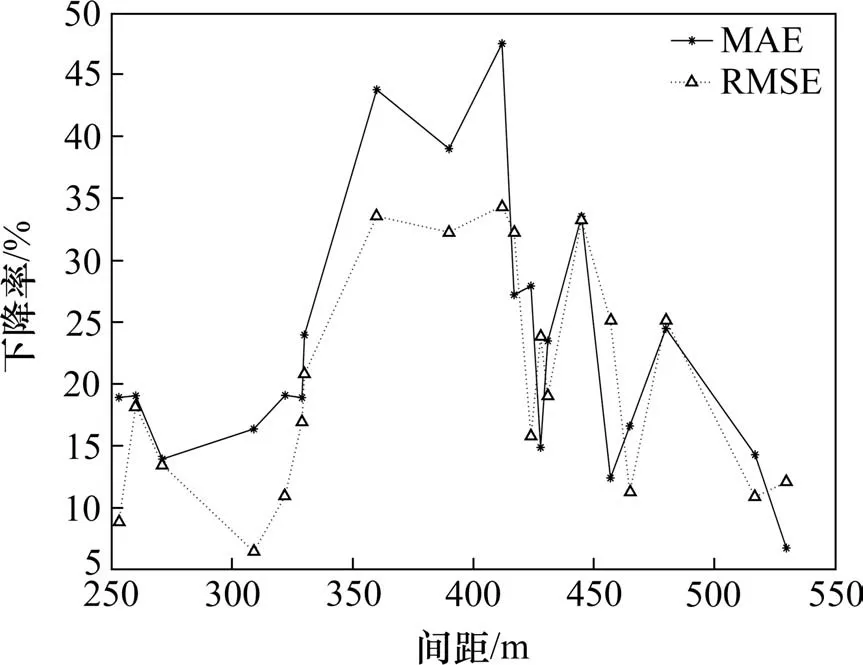
图6 线圈检测器间距与预测误差下降率关系Fig.6 Relationship between loop detector spacing distance and prediction error reduction rate

2.3.2 实证分析检测器数量对于路段交通流量预测影响的关系

上述所有这些都是针对线圈检测器所在的断面交通流量预测结果，下面进行路段交通流量预测效果分析。

根据路段与检测器之间的包含关系，重点选择长路段，例如路段1，路段5 和路段6，计算路段流量预测误差指标。针对每个路段，选择2～K组检测器，分别用2～K组检测器的流量预测路段的流量。分析用不同数量检测器预测路段交通流量与误差指标下降率的关系。

1) 计算出路段1 流量预测误差指标MAE(3)1和RMSE(3)1，选择路段1 中2～7 组检测器分别预测路段1 流量，预测误差指标MAE(4)1和RMSE(4)1。路段1误差下降率与数量的关系如图7所示。

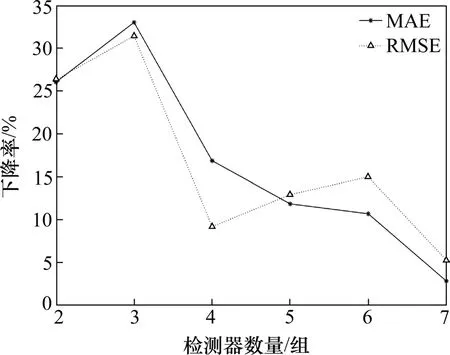
图7 路段1预测误差下降率与线圈检测器数量的关系Fig.7 Relationship between prediction error reduction rate and the number of loop detector for link 1

图8 路段5预测误差下降率与线圈检测器数量的关系Fig.8 Relationship between prediction error reduction rate and the number of loop detector for link 5

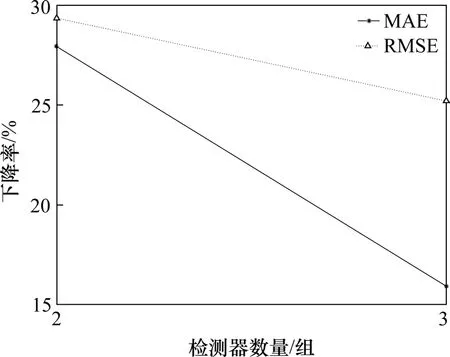
图9 路段6预测误差下降率与线圈检测器数量的关系Fig.9 Relationship between prediction error reduction rate and the number of loop detector for link 6

路段1 的长度为2 300 m，上游位置和下游位置各有1个出口匝道；路段5长度为1 600 m，下游位置有1个出口匝道；路段6长度为1 340 m，上游位置有1 个出口匝道。3 个长路段的上游或下游位置都有匝道，会导致附近线圈检测器精度下降，检测器的数量从中间开始选择。通过分析以上实验结果，对于1 300～2 300 m 的长路段，检测器随机分布情况下，2到3组检测器来预测路段的流量，预测结果的准确度提高较多。进一步，这3个长路段预测效果最好情况下路段1，5，6 分别选择3组、2 组、2 组线圈；预测效果次好情况下路段1，5，6 分别选择2 组、3 组、3 组线圈。这说明对于长路段流量预测问题，仅从长路段中间选择远离匝道口的少量断面线圈交通量即可有效地预测整个路段平均流量。