如何辨析“相似”的简便计算

□ 罗 维

学生在面对“相似”的算式进行简便计算时，容易错用运算定律，教师可以设计相应的辨析活动，帮助学生提升数感，提高计算正确率。

一、整体呈现，聚焦“相似”

1.出示以下题目，要求学生不计算，找出得数相等的算式。

①4×125×8 ②4×8+125×8

③4+125×8 ④125×4+125×8

⑤4×8×125×8 ⑥（4+125）×8

2.学生独立思考后，同桌之间交流答案。

二、分组对比，透析“相似”

1.出示算式②和算式⑥，请学生解释：为什么不计算也会知道这两个算式的得数相等？结合学生的想法，帮助他们基于乘法意义解释原因（如图1）：4个 8 与125 个 8 合起来就是“4+125”个 8，所以不用计算也知道这两个算式一定相等。

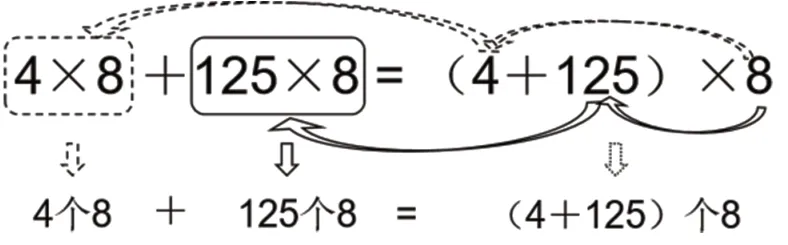
图1

2.引导质疑：算式④中也有 125、4、8 三个数，不通过计算，能解释为什么它的结果和②⑥两个算式不同吗？引导学生依旧通过乘法意义进行解释：算式④125×4+125×8 表示的意思是把4 个 125 和8个125 合起来，结果应该是“4+8”个125，与②⑥两道题表示的“4+125”个8 意义不一样，结果当然不相同。

教师继续追问：意义不一样的算式，结果一定不相同吗？学生讨论得出：意义不一样的算式，结果也有可能相同。比如3×8和4×6的意义不同，结果就是相同的。

3.出示算式⑤，继续引导：这个算式看起来和算式②很像，这两道题的结果会一样吗？学生比较后发现：算式⑤是把“4×8”和“125×8”这两部分相乘，而算式②是把“4×8”和“125×8”这两部分相加（如图2）。根据这两道题的数据看，结果一定不一样。

图2

4.出示算式③，请学生对算式进行修改，使它的得数与算式②⑥的结果相同。

学生修改的方法可能会有这样两种：（1）加上一个小括号，使算式变成（4+125）×8；（2）把加号前面的“4”改为“4×8”，使算式变成“4×8+125×8”。

5.呈现算式①和算式⑥，请学生依旧从算式意义入手，解释这两个算式的结果是否相同（过程略）。

三、拓展练习，强化辨析

呈现下面的习题，请学生独立计算后相互交流。

通过上述活动，学生经历了多轮观察与比较的过程，提升了数感，提高了灵活运用运算定律的能力。