多尺度粗糙接触刚度及数值等效方法研究
2022-03-29马奔奔李源赵伟郭旭刘畅
马奔奔 李源 赵伟 郭旭 刘畅
(1 东方电气风电股份有限公司,研发中心,德阳 618000;2工业装备结构分析国家重点实验室,大连理工大学工程力学系,大连 116023)
0 引言
粗糙界面之间接触刚度的量化对很多工程装配体问题的研究都起到至关重要的作用[1-3],如截面不对称的大型汽发转子槽楔附加刚度稳定性分析、轴承座轴瓦之间接触刚度对系统振动的影响等。然而,界面之间接触刚度的量化依然是较为困难的,主要是因为接触界面上具有很多微观的粗糙峰,且这些粗糙峰具有多尺度和分形的特征(图1),即大粗糙峰上会分布着很多更加细小的粗糙峰。为解决这个难题,有学者利用仿真[4,5]和试验[6]方法对接触刚度进行研究。但是试验和仿真结果具有单一性,往往只适用于当前粗糙样件。目前主流的粗糙接触理论主要有两类:1)Greenwood和Williamson为代表的多峰接触G-W模型[7];2)Persson提出的基于放大率的压力扩散理论[8]。G-W模型具有清晰的物理表征,它假设所有的粗糙峰都可以简化为高度符合高斯分布,且变形相互独立、具有相等曲率半径的球型粗糙峰,而整体接触面上的接触状态可通过对每个粗糙峰的结果进行求和得到。但是G-W模型由于受到单一尺度思想的限制(忽略了粗糙度的多尺度特征和峰间的变形耦合作用),所以被普遍认为在小压缩量的时候比较准确[6,9-11]。相反,Persson提出了粗糙接触理论则是基于放大率的压力扩散方程的一系列数学推导[8],考虑了粗糙表面的多尺度特征。但是受到压力扩散方程中全接触假设的影响,Persson模型往往在大压缩量下被认为比较精确[6,12-14]。
随着计算机技术的发展,粗糙接触界面的仿真方法也得到了飞速的发展。Liu等人[5]采用(法向和切向)弹簧单元来模拟拉杆转子轴承系统中两个圆盘之间的界面接触作用,弹簧单元刚度依赖当前状态下的接触应力。虽然Liu等人的弹簧单元等效方法是有创意且有效的,但不容忽视的是该方法对有限元模型网格划分的质量有着较强的要求,接触界面网格必须严格匹配来保证弹簧单元法向方向不发生偏斜。严格的网格匹配条件还造成了大量的模型细节简化,影响结果的准确性。此外,大量的弹簧单元也意味着耗时的建模过程。
为了能够在整个压缩过程中预测粗糙界面之间的接触状态,近期郭旭等人提出了一个基于放大率的多峰接触MBMA模型[15]。该模型融合了Persson的粗糙表面放大率量化思想和G-W的球型粗糙峰表征方式的优点,考虑了粗糙表面所具有的多尺度和峰间变形耦合的特性,与较多试验[6,16-18]结果相吻合。MBMA模型对本文的研究提供了新的视角,本文将针对工程分析中常见的粗糙表面形貌特征,利用MBMA模型来对粗糙界面接触刚度进行量化研究,使相关工程设计人员通过简单查图表便可以得到较为精确的接触刚度数值。为了能够精确高效地模拟粗糙接触问题,本文将粗糙接触界面等效为一层正交各向异性材料薄层,通过调整薄层的材料属性来精确控制接触界面之间法向和切向接触刚度,以此达到模拟真实粗糙界面之间接触特性的目的。通过在薄层与部件之间施加“绑定”约束,可以进一步地消除接触非线性,极大提高计算效率。
本文在第一章将首先明确接触刚度的物理意义以及粗糙表面的形貌特征,并简要介绍粗糙接触力学MBMA模型。第二章将基于MBMA模型对整个压缩过程中的界面接触刚度的量化进行研究。一种高效的受压粗糙接触界面等效方法及精确性验证将在第三章进行介绍。本文的总结部分放在最后一章。
1 粗糙接触刚度的理论求解
本章将首先明确法向和切向接触刚度的物理意义和表征方式。随后,通过引入粗糙接触MBMA模型来量化接触刚度的求解方法。最后,将针对粗糙表面的形貌特点及其表征方式,归纳影响接触刚度的粗糙表面形貌参数。
1.1 接触刚度的求解方法
对于如图1所示的粗糙接触问题。接触界面法向刚度kn可以计算为[4,19,20]
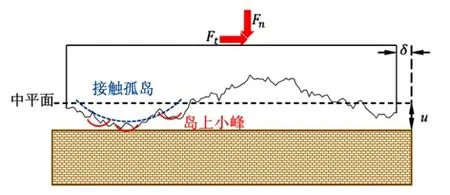
图1 粗糙表面接触状态示意图 Fig.1 The schematic of rough contact problem
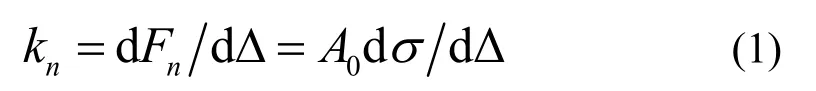
其中,Fn为法向载荷;Δ为接触界面间平均间距u的压缩量,Δ与u的和为常数;A0为名义接触面积;σ为平均接触压应力。切向接触刚度kt可以计算为[5]
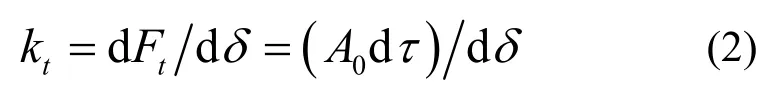
其中,Ft为切向载荷,δ为接触界面间切向的相对位移,τ为平均接触切应力。实际上,切向接触刚度kt对应的是静摩擦接触状态,没有相对滑移发生。基于粗糙表面是各向同性的自仿射分形表面这一假设,Persson等人[19]和Akarapu等人[20]都得到了下述结论
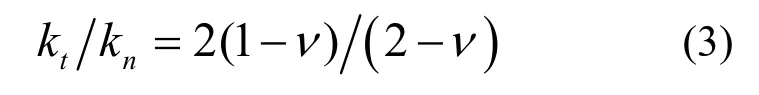
对于常见金属材料,泊松比ν≈0.3,所以kt≈0.82kn。因此,随后本文所提到的接触刚度将都只是法向刚度kn,切向接触刚度kt的数值读者可以根据式(3)得到。
1.2 基于放大率的多峰接触MBMA模型
根据1.1节可知,法向载荷Fn与接触界面间的平均间距u直接关系到界面法向刚度kn的求解。为了求解Fn和u这两个参数,我们这里采用的是郭旭等人提出的一个基于放大率的多峰接触MBMA模型[15]。该模型在整个压缩过程中,都可以精确地、定量地描述真实接触状态。
MBMA模型的建立基于真实的接触是发生在一系列“接触孤岛”上的,在这些接触孤岛上分布着许多更细小的粗糙峰这一物理现象(如图1所示)。所以在当前压缩量下,只有尺寸在某一特定范围内的粗糙峰对该接触孤岛的接触状态起到决定性作用。这是因为小尺寸的粗糙峰将直接被压平,而大尺寸的粗糙峰很难发生变形。根据Greenwood和Tripp[21]的理论便可以解出上述接触孤岛的接触情况,然后整个的接触状态可以通过对每个接触孤岛进行求和得出[15]。
整体法向载荷Fn可以写为

式(4)和式(5)的具体求解方法和参数物理意义,建议参考论文[15],我们这里不再详细展开。最后,将式(1)、式(4)和式(5)联立便可以解得接触界面法向刚度kn。
1.3 粗糙表面的形貌特点及表征方式
式(4)中整体法向接触载荷Fn的数值实际上与粗糙表面的形貌特征有着密切的联系。假设粗糙表面的形貌特征是各向同性的,那么粗糙表面粗糙峰的密度Dsum,粗糙峰峰顶平均的球半径R和粗糙峰顶点高度分布的标准差σ可以分别写为
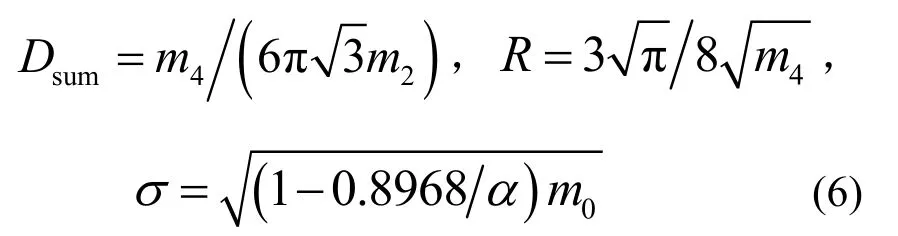
这里α被称为是Nayak参数,并满足
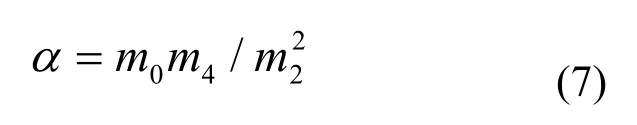
其中,mn称为Nayak矩。通过假定粗糙表面是各向同性的自仿射分形表面[22,23],Nayak矩可以根据式(8)和式(9)求得
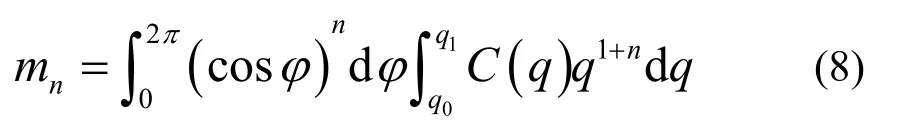
和
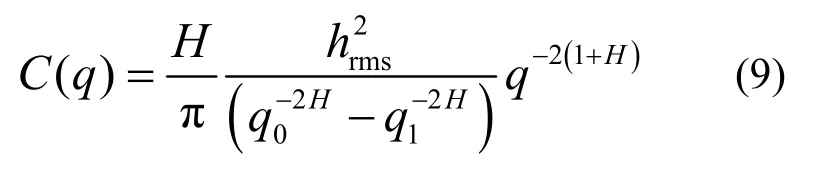
在式(9)中,H是Hurst指数;hrms是表面粗糙度的均方根;q0是长程截断波数(与最大尺度的粗糙峰相关);q1是短程截断波数(与试验可以观测到的最小尺度的粗糙峰相关),其数值等于π除以当前的取样间距。实际测得的波数q的范围依赖于当前的取样方案(如图2所示)。根据上述分析可知,粗糙表面的形貌参数主要由H、hrms、q0和q1这四个变量决定。因此,上述四个变量将直接影响到界面接触刚度kn的数值评估。
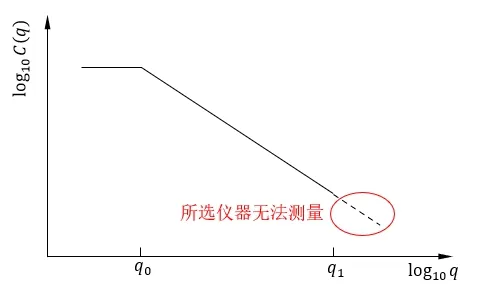
图2 自仿射分形表面的功率谱密度函数[11, 24] Fig.2 Power spectral density function of a detected self-affine surface
2 数值结果
本章将基于MBMA模型对整个压缩过程中的界面接触刚度的量化进行研究。根据1.3节分析可知,H、hrms、q0和q1这四个变量将直接影响接触界面法向刚度kn的预测结果。因此,本章将为上述四个变量选取尽量大的取值范围,涵盖现实中常见的粗糙表面形貌特征,便于读者从本文图表直接量化其所需的接触刚度数值。
2.1 q1对接触刚度的影响
我们知道,粗糙表面上最小尺度的粗糙峰甚至可能为纳米级[11,24]。但是,受到当前测量仪器分辨率的限制,很难探测出粗糙面上所有尺度的粗糙峰。因此,本小节我们将分析能够探测到的截断波数q1对接触刚度的影响。这里粗糙表面的形貌参数定为:Hurst指数H=0.7;设定量q0hrms=0.1;假定能够探测到的最大的波数q1分别为最小波数q0的300,600和900倍。在图3中,我们给出了不同压应力σ下,粗糙接触界面之间的接触刚度。可以看出能够探测到的q1对应的最小尺度粗糙峰几乎不影响接触刚度的数值。这是因为小尺度的粗糙峰尺寸很小,然而压应力的数值却又很高,所以越细小的粗糙峰越容易发生屈服而被压平,对整体刚度起到很小的贡献。
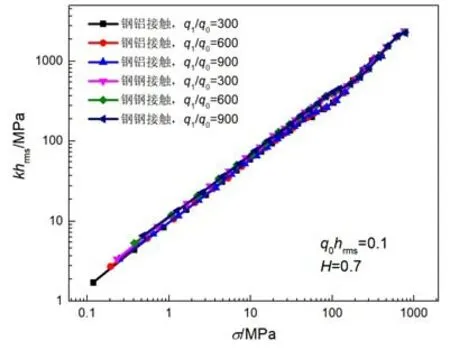
图3 不同能够探测到的最大的波数q1下,粗糙接触界面之间的接触刚度与压应力的关系曲线 Fig.3The relationship between contact stiffness and contact stress under different value of detected q1
2.2 H对接触刚度的影响
常见粗糙表面的 Hurst指数一般满足H≥0.7[23]。因此,我们这里粗糙表面的形貌参数设定为:q0hrms=0.1;能够探测到的最大的波数q1为最小波数q0的300倍。Hurst指数H分别取0.7,0.75,0.8,0.85,0.9。不同压应力σ下,粗糙接触界面之间的接触刚度结果如图4(a)和图4(b)所示。可以看出,H取0.7时,接触刚度的数值稍微高于H取0.9。实际上,分形维数Df与Hurst指数H有着下述关系,即Df=3-H。因此,H的数值越小,表明粗糙峰越“高耸”,因此接触刚度也越大。
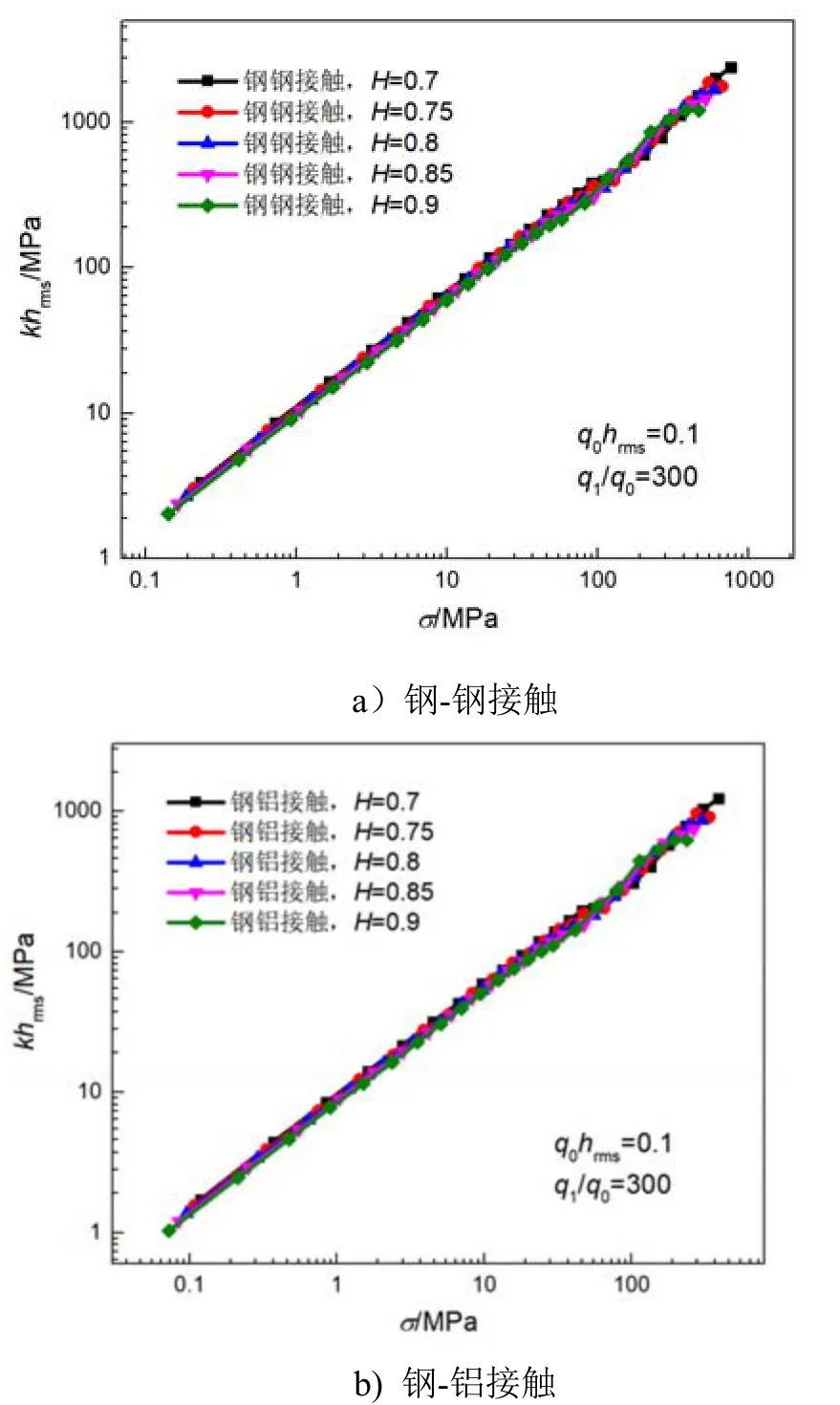
图4 不同Hurst指数H下,粗糙接触界面之间的接触刚度与压应力的关系曲线 Fig.4 The relationship between contact stiffness and contact stress under different value of H
但总的来看,对于Hurst指数H≥0.7的情况,接触刚度数值变化较小,可以近似认为Hurst指数H基本上不影响粗糙表面之间的接触刚度。
2.3 q0hrms对接触刚度的影响
经过前面两个小节的分析,我们知道q1和H基本上不影响或者很小影响粗糙接触界面之间的接触刚度,所以我们这里将对表面粗糙度的均方根hrms和长程的截断波数q0的影响进行分析。此外,经过MBMA理论的研究发现,粗糙界面接触状态往往与q0hrms的乘积有关[15]。因此,我们这里将给定q0hrms的乘积为0.01,0.05,0.1,0.5和1,基本涵盖了常见粗糙表面的参数跨度。
不同q0hrms乘积下,粗糙接触界面之间的接触刚度与压应力的关系曲线如图5所示。可以看出q0hrms的乘积会显著影响接触刚度的数值。鉴于针对大多数经过剖光处理的粗糙表面,hrms一般是微米级的。所以,从图5可以看出当压应力1MPa≤σ≤10MPa时,接触刚度k的量级约在104~105MPa/mm之间;当压应力10MPa≤σ时,接触刚度k的量级约在105~106MPa/mm之间。刘意等人[4,5]的有限元仿真结果与上述接触刚度k量级区间的结论相吻合。
2.4 材料对接触刚度的影响
实际上,不仅仅MBMA理论,其他粗糙接触力学理论,如G-W模型、Persson理论等均研究发现,粗糙界面之间的接触状态与无量纲化后的σ/E*密切相关。其中,1/E*=(1-ν12)/E1+(1-ν22)/E2,为接触等效杨氏模量[15]。E1、E2和ν1、ν2分别为两个接触体的弹性模量和泊松比。所以对于其他的本文没有考虑的接触材料,建议根据图5的解析结果对接触压应力σ进行无量纲化后替换即可。
经过本章分析可以得到以下结论:能够探测到的最小尺度粗糙缝q1、Hurst指数H基本上不影响或者很小影响接触刚度的数值;然而,粗糙度的均方根为hrms、长程截断波数q0会显著影响接触刚度的数值。接触材料属性不同,接触刚度也会显著不同,但读者可以根据图5的解析结果对接触压应力σ进行无量纲化后得到所需接触材料的接触刚度。总的来说,图5基本涵盖了工程分析中常见粗糙表面的接触刚度数值,设计人员可以根据图5采用插值法获得其想要的接触刚度。

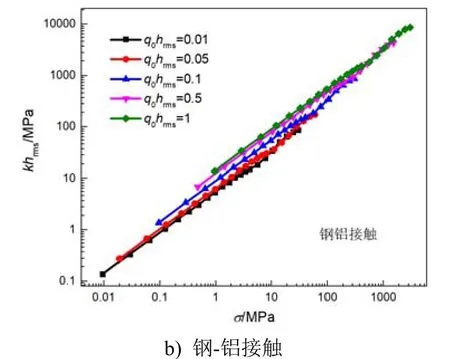
图5 不同q0hrms乘积下,粗糙接触界面之间的接触刚度与压应力的关系曲线 Fig.5 The relationship between contact stiffness and contact stress under different value of q0hrms
3 受压粗糙接触界面等效方法
本章将受压粗糙接触界面等效为一层正交各向异性材料薄层,通过调整薄层的材料属性来精确控制接触界面之间法向和切向接触刚度,以此达到模拟真实粗糙界面之间接触特性的目的。通过在薄层与部件之间施加“绑定”约束,可进一步地消除接触非线性,极大提高计算效率。
3.1 等效正交各向异性薄层法
对于如图6所示的受压粗糙接触问题,接触界面可以等效为一层正交各向异性材料薄层。根据单晶正交各向异性材料的特点,该薄层的本构方程写为

图6 受压粗糙接触界面等效为一层正交各向异性材料薄层 Fig.6 The compressive rough contact interface is equivalent to a thin layer of orthotropic material
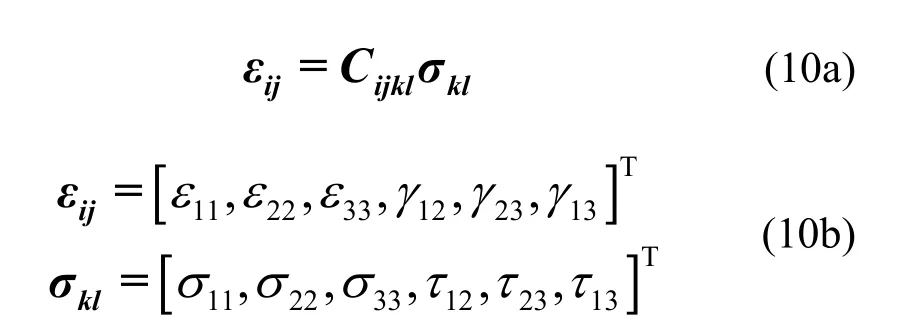
其中,Cijkl为柔度矩阵,εij和σkl分别为应变矢量和应力矢量。对于单晶材料,三个主轴方向上材料的弹性特性相等,故其柔度矩阵可以写为
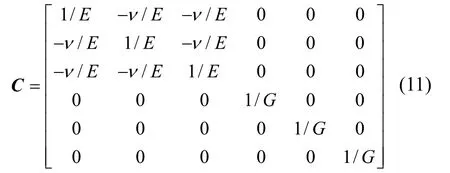
对于图1所示的工况,
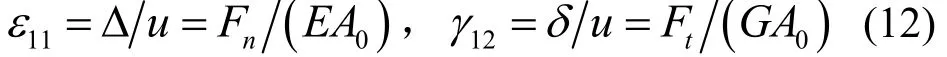
联立式(1)、式(2)和式(12),可得等效的正交各向异性材料薄层的法向接触刚度kn和切向接触刚度kt与材料参数E和G的关系为
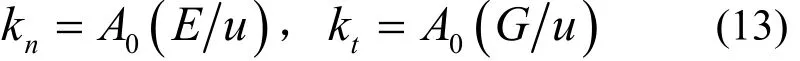
将式(13)形式改写,可得等效的正交各向异性材料薄层的材料参数E和G为
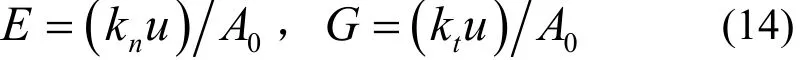
通过在薄层与部件之间施加“绑定”约束,可以进一步消除接触非线性,极大提高计算效率。
3.2 等效薄层法数值验证
为了验证粗糙接触界面的等效正交各向异性薄层法向和切向刚度是否精确可靠,我们基于ABAQUS有限元分析软件建立了一个厚度仅为0.005mm,长度和宽度远大于其厚度值的薄板。在板的厚度方向,仅划分了一层线性单元网格(C3D8单元)。假设已知要模拟粗糙接触界面法向和切向刚度为kn/A0=kt/A0=5×105 MPa/mm,经过式(14),可以算出正交各向异性材料薄层此时对应的材料参数E=G=2500MPa。
当将薄板底面固定,上端面分别施加压应力和切向应力为σ=τ=250MPa,根据式(12)可以解得此时薄板上下端面的法向压缩量和切向相对移动量分别为Δ=δ=5×10-4 mm。
有限元仿真的结果如图7所示,可以看出仿真结果与理论预期相吻合,证明了该等效方法的精确性和可靠性。
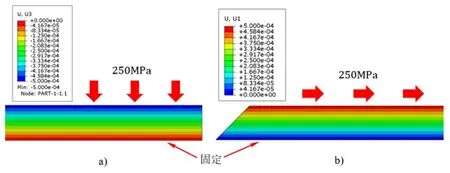
图7 薄板下端面固定:a) 上端面施加250MPa压应力;b) 上端面施加250MPa切应力 Fig.7 Bottom surface of the thin plate is fixed
4 结论
本文基于多尺度粗糙接触力学MBMA模型解析地对粗糙界面的接触刚度进行了量化研究。量化结果涵盖了较宽的粗糙界面形貌参数范围,能够满足工程设计人员获取接触压力从0MPa到1000MPa的接触刚度预测需求。通过接触刚度对粗糙表面形貌参数的敏感性分析,发现不改变接触材料的前提下,能够探测到的最小尺度粗糙缝q1、Hurst指数H基本上不影响或很小影响接触刚度的数值,可以不予考虑;粗糙度的均方根为hrms、长程截断波数q0显著影响接触刚度的数值。进一步还发现,接触材料属性不同,接触刚度也会显著不同,可以根据图5的解析结果对接触压应力进行无量纲化后得到所需的接触材料的接触刚度。
本文图5所示的接触刚度数值基本涵盖了工程分析中常见粗糙表面的形貌特征,对工程师解决相关接触问题研究将提供一定的帮助。随后本文提出了一种粗糙接触界面的等效实现方法。该方法的核心是将粗糙接触界面等效为一层正交各向异性材料薄层,通过调整薄层的材料属性来精确控制接触界面之间法向和切向接触刚度。随后通过在薄层与部件之间施加“绑定”约束,可进一步地消除接触非线性,将非线性接触问题简化为线性问题,极大提高计算效率。最后,本文采用ABAQUS仿真软件对上述等效方法进行了验证,并得到只需一层线性积分单元便可以精确模拟该正交各向异性材料薄层的结论。
