不同运行模式下中深层地埋管换热器取热特性

1 概述

为降低建筑能耗，可再生能源在建筑供暖及供冷中得到了广泛应用

。地热能资源丰富，具有分布广、清洁环保、储量大、稳定可靠等特点

，在建筑领域地热能开发利用中，浅层地埋管地源热泵系统应用较为广泛

，但对空调系统全年冷热负荷平衡度要求比较高

，且地埋管换热器占地面积大。

近年来，中深层地埋管地源热泵系统逐渐成为新兴的地热能利用形式，地埋管换热器占地面积小，对空调系统全年冷热负荷平衡度要求低，取热性能稳定

。Song等人

建立了中深层套管式地埋管换热器数值传热模型，研究结果表明，制热工况下，系统运行初期出水温度下降比较快，并且增大内管的热阻能够有效减少流体热损失。Liu等人

研究表明，循环介质流量对中深层地埋管换热器管内流体的热损失影响比较大，当流量从41.39 m

/h下降到4.52 m

/h，热损失率从25.5%增加到63.7%。Chen等人

采用OpenGeoSys软件对中深层地埋管换热器的取热性能进行了模拟研究，并指出当地温梯度为0.03 ℃/m时，长期运行下的单位钻孔深度换热量不宜大于125 W/m。Cai等人

模拟了中深层地埋管地源热泵系统的4种间歇运行方式，结果表明，不同运行方式下的地埋管换热器出口温降比例不超过3.57%。Liu等人

对影响地埋管换热器性能的12种参数进行了详细分析，并提出长期运行下单位钻孔深度换热量为142 W/m，循环介质进口流速宜为0.7 m/s。孔彦龙等人

采用OpenGeoSys软件对钻孔换热量进行了评估，建议在实际工程设计中单位钻孔深度换热量不宜大于150 W/m。Morgan等人

、Fang等人

运用有限差分法建立数值传热模型，对地埋管换热器取热特性进行研究，并分析了影响地埋管换热器取热性能的主要因素。

由以上内容可知，目前的研究对间歇运行模式的研究比较少。考虑到中深层地埋管地源热泵系统常应用于不同类型的建筑供暖，单一运行模式下的研究结果不宜直接指导其他运行模式下的设计。为此，有必要研究在不同运行模式(运停比)下中深层地埋管换热器的取热特性。

本文建立中深层套管式地埋管换热器数值传热模型，对不同运停比下地埋管换热器连续运行15个供暖期的出水温度、热损失率进行模拟分析。运停比分别设置为24∶0、16∶8、12∶12、8∶16，需要说明的是，运停比并不是严格意义上的比值，仅表示一日中开停机时间的分配。除运停比24∶0为地埋管换热器24 h运行外，其余运停比的地埋管换热器均从9:00开始运行。地埋管换热器供暖期(当年11月15日至次年3月15日)运行，其他时间停机，停机期间岩土处于热恢复期。

将妊娠期高血压患者划分为实验组与常规组，根据患者干预方法分组结果为实验组231例，平均年龄（28.4±4.4）岁，血压范围（135～200）/（90～130）mmHg；常规组227例，平均年龄（27.1±6.1）岁，血压范围（135～200）/（90～130）mmHg。常规组与实验组患者的多项临床资料比较，差异不具有统计学意义（P＞0.05），两组患者具有可比性。

2 数值模型

2.1 物理模型

中深层套管式地埋管换热器物理模型见图1。由图1可知，循环介质(水)采取外进内出方式：由外管环腔流入地埋管换热器，经中深层的高温岩土加热后通过内管流出地埋管换热器。

中深层套管式地埋管换热器的传热过程复杂，且地下岩土环境具有不确定性，因此进行以下设定：忽略地下渗流作用的影响，将岩土中传热视为单纯的导热问题

。忽略地表温度波动的影响

。设定数值模拟区域的径向边界处的温度分布不受地埋管换热器的影响。忽略地埋管换热器内轴向导热。忽略接触热阻。

2.2 控制方程

每层岩土的导热方程为

：

在脊柱一侧加临时固定棒，先截未加固定棒一侧。若截胸椎，要截除肋骨头，从侧面向中间逐渐截除椎体，然后截除椎体前壁，注意保护椎体前方的组织结构。当足够的椎体骨质被去除后，最后截除椎体后壁，在这之前后壁可用于保护后方的硬膜。然后用预弯的临时棒固定截骨侧，移除另一侧的钉棒；用同样的方法截除另一侧的椎体，完全截除椎体和邻近椎间盘后，把钉棒重新固定。先稍松开固定棒的螺钉，缓慢缩小截骨节段上下椎体间隙，然后折弯替换固定的临时棒，逐渐使棒达到预期矫形的角度。椎体间隙的压缩，要在硬膜囊不被皱折的范围内进行。

(1)

式中

——岩土热扩散率，m

/s

——岩土温度，℃

——时间，s

——径向长度，m

——竖直方向长度，m

外管循环水的能量方程为：

(2)

=

式中

——外管单位长度热容量，J/(m·K)

为了验证模型的准确性，我们对西安市某住宅工程进行了现场实测

。在2019—2020年供暖期，共监测了某地热井1 100 h的进出口温度，测试期间单个钻孔的平均换热功率为270 kW，循环水平均质量流量为25.5 t/h，地埋管换热器进出水温差约9.2 ℃，热泵机组的平均制热性能系数达4.7。

——内管循环水温度，℃

——内外管循环水间热阻，(m·K)/W

——钻孔壁温度，℃

——循环水的质量流量，kg/s

——循环水的热容流量，W/K

——外管内直径，m

空间自相关分析基于相关指标来测度要素在空间分布上是否呈现聚集性从全域空间自相关、局部空间自相关两个方面进行分析。

——内管外直径，m

-1

——第

-1层岩土层的底部坐标，m

——循环水的比定压热容，J/(kg·K)

——外管外直径，m

——外管的密度，kg/m

——外管的比热容，J/(kg·K)

2007年中国开始推行绿色金融政策以来，绿色金融在国内逐步兴起并在2015年进入快速发展过程。绿色金融是指为支持环境改善、应对气候变化和资源节约高效利用的经济活动，即对环保、节能、清洁能源、绿色交通、绿色建筑等领域的项目投融资、项目运营、风险管理等所提供的金融服务（中国人民银行等，2016），绿色金融本质仍是金融体系下的一个新领域。因此，绿色金融可以利用有关金融体系支持新兴产业发展的相关研究中存在的影响因子来研究其对生态产业的作用。

——钻孔壁的直径，m

——回填材料的密度，kg/m

统一的管理模式确保在“大数据分析项目”中能有共同的标准、相同的方法和工具，这些数据推动着所有重要的决定，而本土的模式则能提高分析的速度，并确保商业决策者能获得这些见解。

——回填材料的比热容，J/(kg·K)

以露地种植为对照，露地种植平均商品率平均为67.17%，秸秆覆盖带状种植平均商品率为65.44%，较对照低1.73个百分点；膜上覆土种植平均商品率为66.11%，比对照低1.06个百分点；黑色全膜双垄垄侧种植平均商品率为67.7%，比对照高0.53个百分点；黑色全膜大垄面种植平均商品率为72.99%，比对照高5.82个百分点；可降解地膜大垄种植平均商品率为77.6%，比对照高10.43个百分点。

——外管循环水与钻孔壁间热阻，(m·K)/W

发网CEO李平义表示，“双11”印证了发网的发展变迁，历经9年双11考验，发网已形成一套精细化、系统化、体系化的服务体系，能够对整个作业流程和环节进行精细严格的管控，将所有业务所触及的每一个环节系统化地进行管理。通过运用人机互联、设备互联技术实现仓库内的设备、货物和人的数字化。通过引进RFID、AGV、自动存储等模组化的柔性智能设备提升了大规模作业效率和订单处理能力。用稳定的I T系统为双11保驾护航。（李冰漪）

——内管的比热容，J/(kg·K)

在下一节比较震源模型之前，我们先对KiK－Net－BH数据得到的与GPS内插的同震位移进行比较。这两种数据集之间偏差位移矢量的均方根为0.47m，相当于KiKNet－BH 绝对位移矢量（1.25m）均方根的37%。因此，假设大的同震位移与MW9.0东北地震有关，这两种数据集就会非常相似，并提供独立的观测点，这可能对下面介绍的震源模型有影响。

伊秉绶：阴胜国[29]从清初隶书家审美观念的对比中探讨伊秉绶的审美思想，认为伊秉绥的书学思想有3个要点：①取法雄强宽博、静穆方正风格的汉碑；②用笔的中实简省与结体的方正更易；③追求静穆而不失古拙的气息。总之，伊秉绥在审美观念的指引下，凭借自足的勇气和气魄，锐意进取，将隶书革新到底，成功的塑造了崇尚古朴和趋拙避巧的艺术形象，对后来碑派书法的发展产生了深远的影响。

(3)

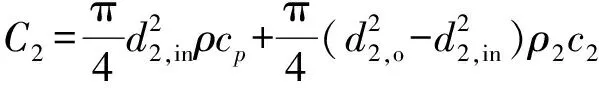
式中

——内管单位长度热容量，J/(m·K)

——内管内直径，m

——内管的密度，kg/m

内管循环水的能量方程为：

式(2)、(3)描述的是在地埋管换热器正常取热工况下的能量方程。当地埋管换热器停运时，内外管循环水的流速为零，此时地埋管周围岩土处于热恢复状态，循环水的热容流量

为0。

外管循环水与钻孔壁间热阻

、内外管循环水间热阻

的计算式分别为：

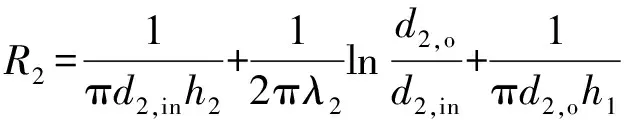
圆柱坐标的径向边界、钻孔底部的温度分布不受地埋管换热器的影响。地表与空气存在对流传热，并设定地表空气温度、表面换热系数保持不变

。

——外管热导率，W/(m·K)

——回填材料热导率，W/(m·K)

——内管内壁表面传热系数，W/(m

·K)

——内管热导率，W/(m·K)

2.3 初始及边界条件

岩土的初始温度分布在径向是均匀的，而在纵向存在地温梯度，并且不同岩土层的地温梯度不同。因此，在大地热流一定的条件下，任一深度的初始岩土温度可表达为

：

建立货币资金业务的授权审批制度，对货币资金业务中的审批人职责范围、审批方式、审批程序及审批责任进行明确，不得随意越权，同时要相互监督。根据授权审批相关制度的规定，审批人要明确各自的审批权限和责任，在授权范围内审批，不得越权审批，同时审批人要对审批事项进行详细审核，并对各自审批意见负责。经办人在职责范围内，根据审批意见来办理业务，对于审批人超越权限的审批，经办人要拒绝办理，同时要向上级授权部门报告。对于重要的资金支付业务，要实行集体决策和审批，并建立责任追究制度，防止各种违规事项的发生，防范资金风险，防止资金损失。

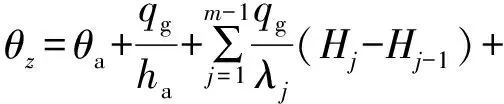
(4)

式中

——任一深度的初始岩土温度，℃

此后，东芝宣布将出售核时代，并于2017年12月宣布韩国电力公司(Kepco)为优先竞标人。但在英国政府2018年6月宣布将采用“受监管的资产基础”(RAB)的项目融资模式后，东芝宣布取消韩电的优先谈判权，为其他竞标者留出机会。

——地表温度，℃

——大地热流，W/m

——地表的表面传热系数，W/(m

·K)

——岩土的分层数量

——第

层岩土层的热导率，W/(m·K)

——第

层岩土层的底部坐标，m

——循环水的密度，kg/m

——第

层岩土层的热导率，W/(m·K)

——第

层岩土层的底部坐标，m

-1

——第

-1层岩土层的底部坐标，m

式(4)中，当

=1时，

为地表高度(值为0)。

式中

——外管内壁、内管外壁表面传热系数，W/(m

·K)

而红宝石与蓝宝石主要的区别就在于，它们在各自生长的过程中捕获的致色元素不同。红宝石捕获了元素铬，呈红色、紫红色，蓝宝石捕获的是元素铁和钛。由于铁和钛在每个宝石中含量和比例不同，所以宝石生成之后呈现出的颜色深浅也不一样。

边界条件为：

(5)

=

,

=

(6)

式中

——热泵蒸发器换热功率，kW，本文取200 kW

——地埋管换热器高度，m

3 模型求解与验证

研究方法为对控制方程离散后编制程序求解。

3.1 模型求解

在非稳态数值传热模拟中，时间步长、纵向(

方向)步长、径向(

方向)步长对模拟计算速度及结果精确度均有一定影响。

在网格划分的过程中，考虑径向较远处热流趋近于0，钻孔附近的热流及温度梯度比较大，因此以钻孔壁为界采用变步长(即径向步长按照等比级数变化，等比系数取1.2

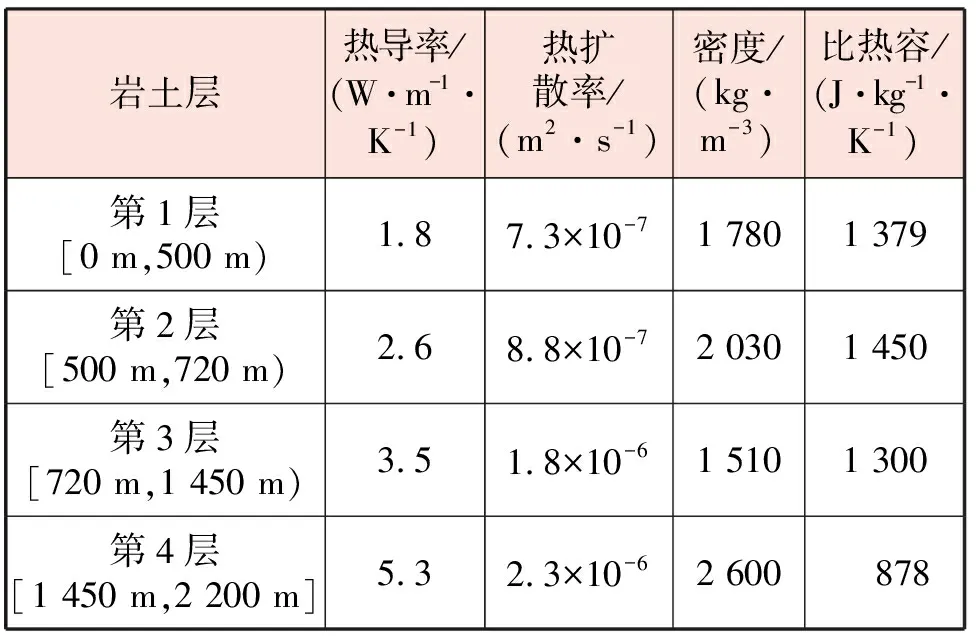
)。由无关性验证结果可知，当网格节点数取7 700个时可满足计算精度要求，即径向共取40个节点，距离钻孔壁第1个节点的距离为0.168 m，圆柱坐标的径向边界为119.1 m。纵向步长取10 m，时间步长取900 s。模拟所需的物理参数见表1，岩土层划分及岩土热物性参数

见表2。

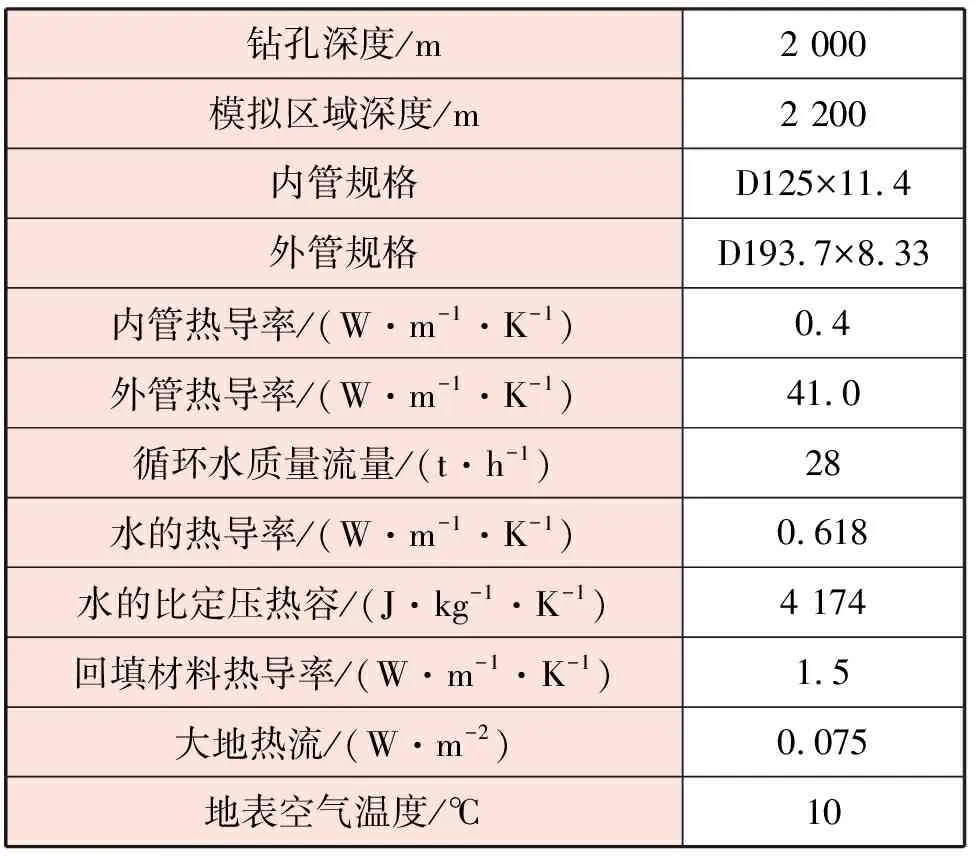
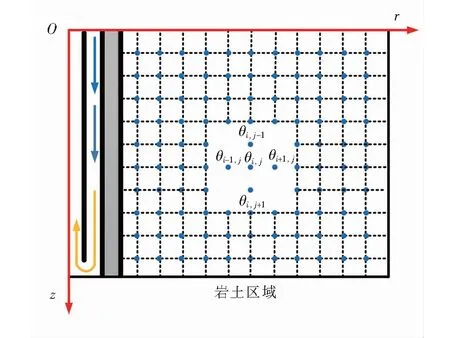
可将中深层地埋管换热器与周围岩土的耦合传热问题视为圆柱体的二维瞬态导热，式(1)～(6)构成了数值传热模型，并经过无关性验证可采用有限差分法将上述控制方程进行离散求解。离散网格见图2。

3.2 模型验证

——外管循环水温度，℃

将该地热井运行参数导入模型，模拟地埋管换热器进出口水温。由模拟结果及实测结果

可知，二者的相对误差在±6.0%之内，满足工程要求。

4 结果与分析

4.1 出水温度

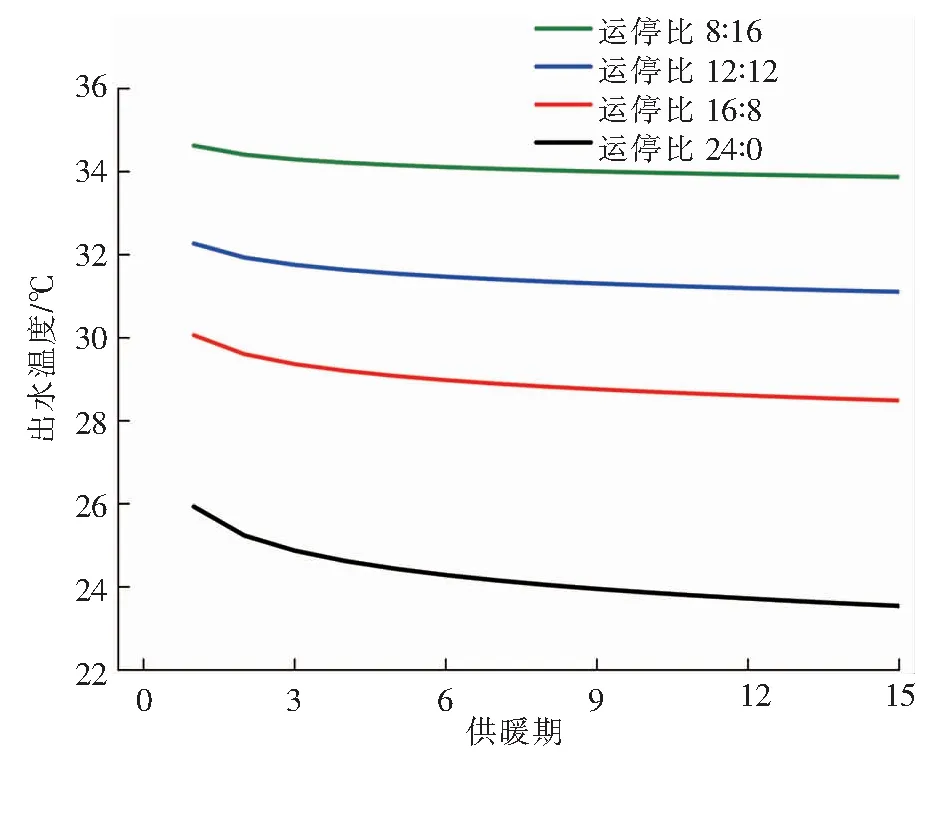
在循环水初始温度分别为35.6、36.5、36.9、37.8 ℃条件下，模拟4种运停比地埋管换热器连续运行15个供暖期的出水温度。4种运停比供暖期结束时地埋管换热器的出水温度见图3。由图3可知，随着运行时间的延长，4种运停比(8∶16、12∶12、16∶8、24∶0)供暖期结束时地埋管换热器的出水温度逐年降低，前期温降速率比较大，后期比较平稳。相同供暖期，供暖期结束时地埋管换热器的出水温度由高到低对应的运停比顺序为：8∶16、12∶12、16∶8、24∶0，以第1个供暖期结束时地埋管换热器的出水温度为基准，第15个供暖期结束时地埋管换热器的出水温度分别下降2.18%、3.61%、5.23%、9.23%。由模拟结果可知，第15个供暖期末，运停比8∶16、12∶12、16∶8、24∶0对应的地埋管底部的循环水温度分别为39.70、33.97、36.71、28.93 ℃。由以上分析可知，降低运停比有利于岩土热恢复，提高热泵机组的制热性能。

（119）多瓣苔 Macvicaria ulophylla（Steph.）S.Hatt.马俊改（2006）

4.2 热损率

对于循环水采取外进内出方式的套管式地埋管换热器，循环水由外管达到地埋管底部时，温度达到最高，循环水的热功率达到最大。循环水在由地埋管底部通过内管向上流动过程中发生热损失，地埋管换热器出口循环水热功率为实际热功率。因此，地埋管换热器热损失率

的表达式为：

式中

——地埋管换热器热损失率

——循环水实际热功率，W

——循环水最大热功率，W

——地埋管底部循环水温度，℃

——地埋管出水温度，℃

——地埋管进水温度，℃

由模拟结果，计算得到运停比8∶16、12∶12、16∶8、24∶0对应的地埋管换热器热损失率分别为48.86%、50.07%、51.09%、52.40%。由计算结果可知，降低运停比有利于减小热损失率。

5 结论

① 随着运行时间的延长，4种运停比(8∶16、12∶12、16∶8、24∶0)供暖期结束时地埋管换热器的出水温度均逐年降低，前期温降速率比较大，后期比较平稳。相同供暖期，供暖期结束时地埋管换热器的出水温度由高到低对应的运停比顺序为：8∶16、12∶12、16∶8、24∶0，以第1个供暖期结束时地埋管换热器的出水温度为基准，第15个供暖期结束时地埋管换热器的出水温度分别下降2.18%、3.61%、5.23%、9.23%。由模拟结果可知，第15个供暖期末，运停比8∶16、12∶12、16∶8、24∶0对应的地埋管底部的循环水温度分别为39.70、33.97、36.71、28.93 ℃。降低运停比有利于岩土热恢复，提高热泵机组的制热性能。

② 运停比8∶16、12∶12、16∶8、24∶0对应的地埋管换热器热损失率分别为48.86%、50.07%、51.09%、52.40%。降低运停比有利于减小热损失率。

[1] YANG H，CUI P，FANG Z. Vertical-borehole ground-coupled heat pumps: A review of models and systems[J]. Applied Energy，2010(1)：16-27.

[2] AMASYALI K，EL-GOHARY N M. A review of data-driven building energy consumption prediction studies[J]. Renewable and Sustainable Energy Reviews，2018，81：1192-1205.

[3] LIU J，WANG F，GAO Y，et al. Influencing factors analysis and operation optimization for the long-term performance of medium-deep borehole heat exchanger coupled ground source heat pump system[J]. Energy and Buildings，2020， 226： 110385-1-7.

[4] 满意，姜国心，杜甜甜，等. 利用弃井开采中深层地热能名义取热量的模拟[J]. 山东建筑大学学报，2019(4)：20-24.

[5] SONG X，WANG G，SHI Y，et al. Numerical analysis of heat extraction performance of a deep coaxial borehole heat exchanger geothermal system[J]. Energy，2018，164：1298-1310.

[6] LIU J，WANG F，CAI W，et al. Numerical study on the effects of design parameters on the heat transfer performance of coaxial deep borehole heat exchanger[J]. International Journal of Energy Research，2018(12)：6337-6352.

[7] CHEN C，SHAO H，NAUMOV D，et al. Numerical investigation on the performance， sustainability， and efficiency of the deep borehole heat exchanger system for building heating[J]. Geothermal Energy，2019(1)：7-18

[8] CAI W，WANG F，LIU J，et al. Experimental and numerical investigation of heat transfer performance and sustainability of deep borehole heat exchangers coupled with ground source heat pump systems[J]. Applied Thermal Engineering，2019，149：975-986.

[9] 孔彦龙，陈超凡，邵亥冰，等. 深井换热技术原理及其换热量评估[J]. 地球物理学报，2017(12)：4741-4752.

[10] MORGAN L L，LARROQU F，DUPUY A，et al. Thermal performance of a deep borehole heat exchanger：Insights from a synthetic coupled heat and flow model[J]. Geothermics，2015，57：157-172.

[11] FANG L，DIAO N，SHAO Z，et al. A computationally efficient numerical model for heat transfer simulation of deep borehole heat exchangers[J]. Energy and Buildings，2018，167：79-88.

[12] PIECHOWSKI M. Heat and mass transfer model of a ground heat exchanger：Validation and sensitivity analysis[J]. International Journal of Energy Research，1998(11)：965-979.

[13] 刘晓燕，赵军，石成，等. 土壤恒温层温度及深度研究[J]. 太阳能学报，2007(5)：494-498.

[14] 贾力，方肇洪，钱兴华. 高等传热学[M]. 北京：高等教育出版社，2008：5-10.

[15] 杜甜甜，满意，姜国心，等. 套管式中深层地埋管换热器传热建模及取热分析[J]. 可再生能源，2020(7)：887-892.

[16] 杜甜甜，满意，姜国心，等. 中深层地埋管换热器最佳钻孔间距的模拟研究[J]. 煤气与热力，2019(11)：A21-A24.

[17] LI J，XU W，LI J，et al. Heat extraction model and characteristics of coaxial deep borehole heat exchanger[J]. Renewable Energy，2021，169：738-751.